基于区间分块Q学习的智能车辆安全舒适刹车算法
2024-02-18余欣磊周贤文张依恋顾伟
余欣磊 周贤文 张依恋 顾伟
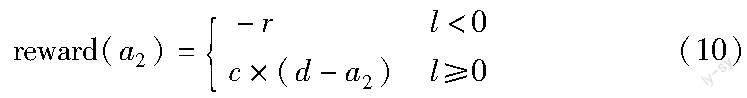
摘 要:针对当前智能汽车刹车场景下的安全与舒适性问题,提出一种基于区间分块的Q学习算法。首先在Q表中将前车加速度以一定间隔划分入等长区间,用区间中值做间隔来划分后车加速度。其次通过在安全条件下与加速度呈负相关的奖励设置,使智能体在保证安全的前提下尽量降低刹车加速度。最后在智能体训练的过程中遵循ε-贪心策略以减少随机性,在训练完毕后遵循贪心策略以最大程度利用智能体。将提出的算法与传统Q学习算法在三种常见道路场景上进行仿真测试。实验结果显示使用提出算法的智能车辆在刹车场景中安全率100%、平均刹车加速度小于2 m/s2且能处理连续刹车加速度,表明提出的算法能够在确保智能汽车安全刹车的同时实现较低的刹车加速度。同时在连续刹车加速度与离线环境等复杂情况下,算法均能正常使用。
关键词:智能汽车;智能刹车;Q学习;区间分块
中图分类号:TP391 文献标志码:A 文章编号:1001-3695(2024)01-027-0183-05
doi:10.19734/j.issn.1001-3695.2023.05.0220
Interval-block-based Q-learning algorithm for safe and comfortable braking of intelligent vehicles
Abstract: To address the safety and comfort issues in intelligent vehicle braking scenarios,this paper proposed a Q-learning algorithm based on interval partitioning.Firstly,the algorithm divided the acceleration of the preceding vehicle into equal-length intervals with a certain interval in the Q-table,and used the interval median to partition the acceleration of the following vehicle.Secondly,the algorithm used a reward function that was negatively correlated with acceleration under safe conditions to encourage the agent to minimize braking acceleration while ensuring safety.Finally,the algorithm followed the ε-greedy strategy during the training of the agent to reduce randomness,and followed the greedy strategy after training to maximize the utilization of the agent.This paper simulated the proposed algorithm and the traditional Q-learning algorithm on three common road scenarios.The experimental results show that the intelligent vehicle used the proposed algorithm has a 100% safety rate in braking scenarios,with an average braking acceleration of less than 2 m/s2,and can handle continuous braking acceleration,which indicates that the proposed algorithm can achieve lower braking deceleration to improve passengers comfort while ensuring safe braking of the intelligent vehicles.In addition,the algorithm is effective in complex scenarios including continuous braking deceleration and offline environments.
Key words:intelligent vehicle;intelligent braking;Q-learning;interval block
0 引言
目前智能網联技术快速发展,各类互联网行业巨头纷纷涌入,智能汽车领域正成为新一轮科技革命和产业革命的战略高地。随着智能汽车数量的不断增加,我国智能汽车行业也将迎来发展的黄金期[1]。在发展过程中,智能汽车暴露出一些问题,如因使用互联网而带来的网络安全问题[2]、因紧急刹车导致的汽车追尾等安全问题[3]。据统计,我国因公路事故伤亡的死亡率高达30%(发达国家仅3%~4%)[4],而在汽车道路交通事故中,追尾问题占70%以上。其中,紧急刹车是导致追尾问题的一个重要诱因,因此,做好紧急刹车的有效应对,对于规避因汽车追尾产生的交通事故至关重要。
针对紧急情况下如何安全刹车这一问题,近年来已有许多专家学者进行了研究,2009年,Mamat等人[5]通过一个模糊逻辑控制器(fuzzy logic controller,FLC)将驾驶员的常见行为量化为一系列的规则并对其进行设计,从而对智能汽车的刹车进行自动控制。文献[6]提出自动紧急刹车系统(automated emergency braking system,AEBS),主要依靠新兴的传感器技术,通过车载传感器获取前后车距离,进行机器条件判断,最终决定是否刹车以及刹车力度调节。文献[7]利用一个集成芯片对智能汽车刹车进行控制。文献[8]采用深度强化学习的方法进行智能决策。随着深度学习(deep learning,DL)的发展,尤其是深度强化学习在围棋和其他电脑游戏下的展示,强化学习(reinforcement learning,RL)吸引了越来越多专家学者们的关注[9]。强化学习又称为增强学习[10],是机器学习下的一个分支,区别于监督学习与无监督学习,强化学习不存在人为指导和方法,完全由机器对策略集进行学习。可以理解为强化学习智能体在与环境进行交互的过程中,通过不断地尝试,从错误中学习经验,并根据经验调整其策略,来最大化最终所有奖励的累积值[11]。这使得强化学习具有很强的环境适应力,训练完成后的智能体可以独立工作,无须外界帮助。汽车刹车场景兼具时间短、网络不稳定、场景复杂等特性,因此刹车控制器必须高效稳定且能应对复杂场景。而强化学习相较传统的控制器设计算法效率更高,训练完成后的智能体可不依赖网络独立工作,且对非线性问题处理非常有效。因此,强化学习十分切合汽车紧急刹车场景。
目前已有较多关于Q学习的研究,文献[12]通过双层深度Q神经网络(double deep Q network,DDQN)研究飞机姿态控制,文献[13]提出一种基于等效因子的汽车能量控制策略,文献[14]提出一种基于双Q表与启发式因素的Q学习并将其应用于无人机空战,但这些Q学习很少与汽车刹车问题联系在一起,且几乎没有考虑乘客舒适度问题。然而,随着人们对乘车舒适性需求的不断提高,如何在保证安全的基础上提升乘客乘车舒适度成了紧急刹车问题的一个研究重点。
本文采用强化学习中的Q学习实现智能车辆的安全舒适刹车,并在此基础上,通过区间分块方法改进Q学习,改进后的Q学习可以处理连续状态空间问题。本文所做的工作主要有:a)结合实际驾驶场景,将汽车刹车问题转换为强化学习问题,并考虑乘客舒适度,在安全刹车的前提下改善乘客体验。b)提出区间分块方法,对传统Q学习算法改进,改进后的算法能够有效处理连续状态空间问题,切合实际汽车刹车场景。
1 模型与算法
1.1 汽车跟驰模型
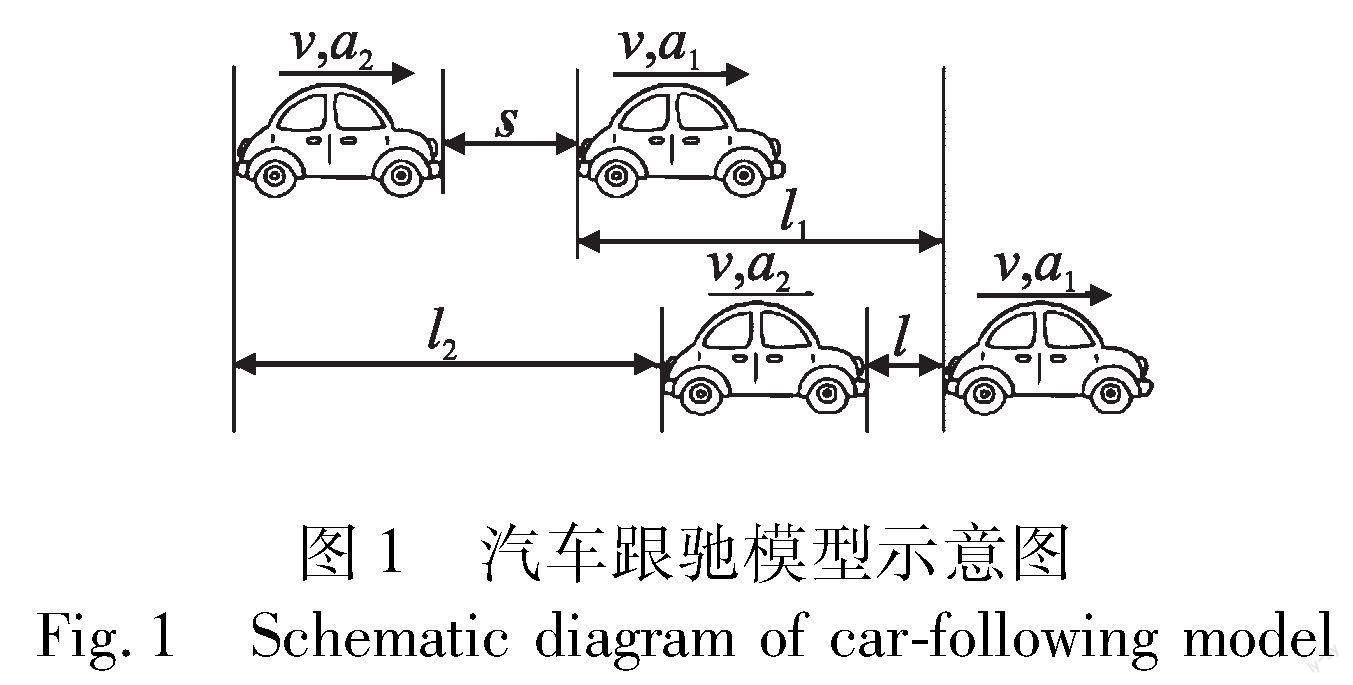
本文考虑文献[15]中的汽车跟驰模型,该模型包含前后两辆汽车,其中s代表两车初始相隔距离,v代表两车速度,a1代表前车刹车加速度,a2代表后车刹车加速度,l1代表前车刹车距离,l2代表后车刹车距离,l代表两车最终相隔距离,具体如图1所示。
考虑如图1所示模型,两车以相同的速度行驶,在某一时刻因突发情况,前车以一定的加速度开始刹车,后车随即以一定的加速度跟随前车开始刹车。本文假设前后两车的初始相隔距离满足《中华人民共和国道路交通安全法实施条例》中的安全距离,即两车距离(m)在数值上等于两车速度(km/h)。
根據模型可以得出,前车刹车距离为
后车刹车距离为
两车最终相隔距离为
要保证安全刹车,后车的最小加速度为
假设舒适加速度为ac,则可得到表1关系。
1.2 Q学习算法
强化学习由智能体和环境两部分组成,智能体是训练的对象,除智能体外均属于环境。在学习过程中,智能体从环境中获取状态信息,根据策略给出相应的动作,环境接收智能体动作后再传递回新的状态信息与奖励。在与环境的不断交互中,通过值函数来评价智能体的好坏[16]。
Q学习是最有效的强化学习独立模型算法之一[17]。Q学习的核心在于创建一个Q表,将状态(state)与动作(action)定义为行与列,某一行对应某一种状态,某一列对应某一种动作,对应行列里的值Q(state,action),一般简写为Q(S,A),即对应状态下采取对应动作的动作值函数。动作值函数反映的是智能体在某一状态下采取某一动作的价值,动作值函数越大说明在对应状态下采取对应动作的价值越大,智能体一般就越倾向于选取该动作。通过不断训练,最终得到一个Q表。通过读取Q表,即可根据对应状态采取对应动作。智能体是训练的目标,本质是Q表,在汽车跟驰模型中代表的是根据前车加速度a1选择后车加速度a2的策略集。状态S是前车加速度a1,状态空间是所有前车加速度a1构成的集合;动作A是后车加速度a2,动作空间是所有后车加速度a2构成的集合,Q(S,A)是某一确定前车加速度a1下采取某一确定后车加速度a2的价值。奖励是关于最终相隔距离l和后车加速度a2的一个函数,在训练智能体时遵循的是ε-贪心策略,训练完成后,智能体遵循的是贪心策略。智能体训练示意图如图2所示。
贪心策略就是在任意状态下智能体只选择该状态下Q(S,A)最大的动作,数学表达为
π(a|s)=arg maxQ(s,a)(5)
Π是智能体的策略集,Π(A|S)就是指在状态S时智能体选择动作A的策略。ε-贪心策略则是在任意状态下以ε的概率随机选择该状态下的动作,以1-ε的概率选择该状态下Q(S,A)最大的动作,数学表达为
之所以在训练和使用智能体时使用两种不同的策略,是为了处理智能体的探索-利用困境。如果智能体一味地利用先前的经验,很容易因为前期的随机性,导致最终陷入局部最优。如果智能体一味地探索,在有限状态空间下会花费大量时间,在无限状态空间下会陷入死循环。所以在训练时遵循ε-贪心策略,既保证对经验的利用,又保留了一定的探索,减少智能体陷入局部最优的概率。在最终训练完成后则遵循贪心策略,最大程度利用智能体的经验以获取最大收益。
1.3 区间分块Q学习算法
传统Q学习算法适用于离散状态空间问题,无法处理现实情况下的连续状态空间问题。因为传统Q学习中的Q表是一个固定大小的有限表格,这就要求传统Q学习必须知道所有状态信息与动作,才能将其一一填入Q表,进而加以训练。Q学习本质是对Q表进行搜索迭代优化,Q表搜索维度越小,Q学习收敛速度越快。传统Q学习搜索维度数学表达为
d=m×n(7)
其中:d是Q学习的搜索维度;m是状态空间下状态的数量;n是动作空间下动作的数量。在连续状态空间下,状态的数量是无限的,即m趋于无穷大,所以d趋于无穷大,Q学习就无法收敛,问题无法解决。
本文提出一种区间分块方法,以区间的形式表示状态空间,将状态空间内连续的状态按照一定的间隔划入等长的离散区间块中,以离散的区间块代表这个区间内所有连续的状态,则问题的搜索维度d*就简化为
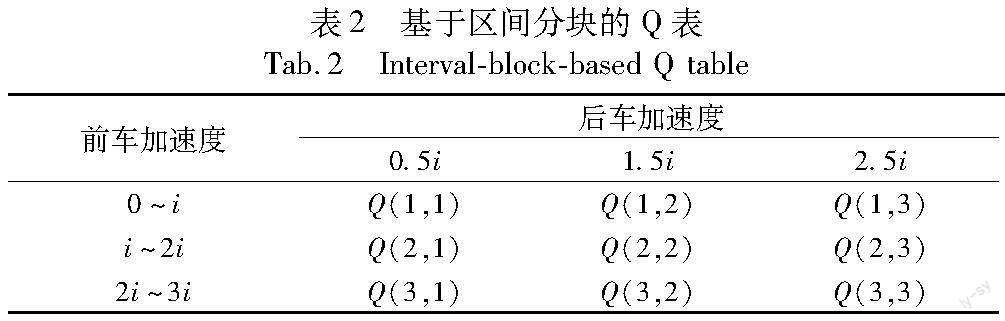
其中:m*是将状态空间以区间形式表示的长度,i是区间划分的间隔。不论状态空间内包含多少种状态,以区间形式划分都可以将其变成离散的区间块,问题的搜索维度就大大下降了。结合汽车刹车场景,后车只要保持与前车一致的刹车加速度即可保证安全刹车,所以当前车加速度以区间形式划分后,以区间的中值来划分后车加速度,很符合安全刹车的先验知识。具体Q表如表2所示。
表格中Q(1,1)代表第一种状态(前车加速度处于0~i m/s2)下选取第一种动作(后车加速度变为0.5i m/s2)的价值。Q(1,1)越大,代表该状态下选取该动作的价值越大,智能体就越倾向于在该状态(前车加速度处于0~i m/s2)下选取该动作(后车加速度变为0.5i m/s2)。
Q(S,A)的大小由奖励函数累加确定:
Q(s,a)=Q(s,a)+reward(a2)(9)
其中:reward(a2)是奖励函数,数学表达为
其中:l为两车最终相隔距离(l<0代表两车相撞,因此奖励为负,l>0时通过d-a2使后车加速度尽量减少);c是权重系数,减小前期因随机性探索产生的优势,使智能体尽可能多地探索,减少智能体陷入局部最优的概率。区间分块方法通过对前车加速度的区间划分解决了连续状态空间下搜索维度无限的问题,结合实际场景中汽车安全刹车的先验知识,对后车加速度按前车加速度区间中值划分,算法的整体流程如下所示。
输入:两车初始相隔距离s、两车速度v、前车加速度a1。
输出:后车加速度a2。
while 1 do
初始化Q表,stop=0
for i=0,episode do
初始化前车加速度
区间分块前车加速度
纯随机探索
探索与利用
确定奖励
end for
for i=1,number do
if 训练达标
stop+=1
end if
end for
if stop==number
end if
end while
2 实验与分析
2.1 实验环境与总仿真
本文使用 PyCharm建立仿真系统,全程在无网络状态下进行,验证改进Q学习算法刹车的安全性、舒适性与连续性。将本文的改进Q学习算法与传统Q学习算法在城市道路、城市快速路、高速公路三种情况下进行对比,特别指出,此处的传统Q学习算法采用了与本文改进Q学习算法一致的奖励设置,但是没有使用区间分块,目的是证明区间分块方法对连续状态空间问题的处理能力。
根据文献[18]对人体震动和乘坐舒适性的大量评估研究,本文设定舒适加速度ac为2 m/s2,路面可提供的最大加速度为amax为5 m/s2。在0~5 m/s2的加速度区间内,i取1 m/s2则智能体不够精确,i取0.01 m/s2则训练效率偏低,因此综合智能体准确性与训练效率,选取i为0.1m/s2。
本文对三种路面情况在各进行100万次仿真测试,因为0~1 m/s2前车加速度过小,导致最终相隔距离远超其余区间,所以将前车加速度在1~5 m/s2随机产生。最终相隔距离大于0视为安全刹车,将数据整理如表3所示。
2.2 城市道路仿真
城市道路限速为60 km/h,对应的安全跟车距离为60 m,因为城市事故多发生于超速时,所以本文使用s=72 m,v=20 m/s,即72 km/h两车速度与72 m两车初始相隔距离模拟城市道路紧急刹车情况。
图3(a)是后车加速度折线图,将前车加速度以0.1 m/s2为间隔从0~5 m/s2进行划分,圆形点代表传统Q学习曲线,五角星点代表改进Q学习曲线。由图可知,改进Q学习与传统Q学习均能控制加速度在舒适加速度内,证明改进Q学习算法刹车的舒适性。图3(b)是改进Q学习下最终相隔距离图,由图可知,改进Q学习下最终相隔距离始终大于0,即汽车始终安全刹车。特别指出由于在0~1 m/s2区间前车加速度过小,导致最终距离远超其余区间,所以将1~5 m/s2区间放大显示,由放大图可清晰看出,即使前车加速度取5 m/s2,也有100 m以上的最终相隔距离,证明改进Q学习算法刹车的安全性。图3(c)是后车加速度散点图,当在0~5 m/s2按0.1 m/s2间隔均匀产生50个前车加速度时,因为设置在传统Q学习离散点上,所以传统Q学习与改进Q学习均能给出相应后车加速度。当在0~5 m/s2内随机产生50个前车加速度时,因为几乎不可能在传统Q学习离散点上,所以传统Q学习无法处理,只能给出0 m/s2的后車加速度,而改进Q学习依然能给出相应的后车加速度。所以由图可知,通过区间分块方法改进的Q学习可以有效处理连续前车加速度问题,而传统Q学习则无法解决,证明了改进Q学习算法刹车的连续性。
2.3 城市快速路仿真
城市快速路限速在60~100 km/h,具体由路况决定,对应的安全跟车距离为60~100 m,因为城市快速路超速较少,但高速行驶时事故发生的概率较高,所以本文使用s=90 m,v=25 m/s,即90 km/h两车速度与90 m两车初始相隔距离模拟城市快速路紧急刹车情况。图4(a)是后车加速度折线图,由图可知,改进Q学习与传统Q学习均能控制加速度在舒适加速度内,证明改进Q学习算法刹车的舒适性;图4(b)是改进Q学习下最终相隔距离,由图可知,改进Q学习下最终相隔距离始终大于0,即汽车始终安全刹车;图4(c)是后车加速度散点图,结论与上文类似。
2.4 高速公路仿真
高速公路限速在100~120 km/h,具体由车道决定,对应的安全跟车距离为100~120 m,因为高速公路超速较少,且车辆大多低速行驶,所以本文使用s=108 m,v=30 m/s,即108 km/h两车速度与108 m两车初始相隔距离模拟高速公路紧急刹车情况。
图5(a)是后车加速度折线图,由图9可知,改进Q学习与传统Q学习均能控制加速度在舒适加速度内,证明改进Q学习算法刹车的舒适性;由图5(b)可知,改进Q学习下最终相隔距离始终大于0,即汽车始终安全刹车;图5(c)是后车加速度散点图,结论与上文类似。
2.5 算法总结
总仿真实验中使用改进Q学习算法对三种路面情况各进行了100万次测试,安全率均为100%,体现了算法的安全性与稳定性;平均相隔距离城市道路为303 m,城市快速路为421 m,高速公路为562 m,因为在高速情况下,即使微小的扰动也会产生巨大的影响,所以智能体提前预留更远的平均相隔距离以应对实际情况。平均刹车加速度城市道路为1.48 m/s2,城市快速路为1.65 m/s2,高速公路为1.80 m/s2,因为高速情况下过低的加速度无法保证安全刹车,智能体必须优先确保安全性,再考虑舒适性。最终三种路面情况的平均刹车加速度仍符合舒适刹车加速度,体现了算法的安全性与舒适性。
三种道路仿真实验中,结合图3(a)、图4(a)、图5(a)可以看出:城市道路上,智能体始终将加速度控制在2 m/s2以下;城市快速路上当前车刹车加速度大于4.5 m/s2时,智能体将加速度超出2 m/s2;高速公路上当前车加速度大于3.5 m/s2时,智能体已将加速度超出2 m/s2。因为在城市道路的低速情况下,智能体始终可以保证安全刹车,随着速度的增高,在城市快速路上,智能体会采取更高的刹车加速度以优先确保安全性,在高速公路上更是如此。所以图3(b)、图4(b)、图5(b)中智能体始终保持了安全的最终相隔距离:城市道路上均大于100 m;城市快速路上均大于150 m;高速公路上均大于200 m。其体现了该算法在优先确保安全性的前提下尽可能地实现了舒适性。结合图3(c)、图4(c)、图5(c)可以看出,传统Q学习在面对连续前车加速度时无法处理,只能在离散前车加速度时处理,而改进Q学习均能处理,其体现了算法的连续性。
3 结束语
针对智能车辆安全舒适刹车问题,本文提出了一种基于区间分块的Q学习算法,使用速度与两车初始相隔距离对三种常见路面进行仿真,并与传统Q学习算法进行了对比。仿真结果表明,提出的算法能够在确保智能汽车安全刹车的同时实现较低的刹车加速度,能够处理连续前车刹车加速度问题且无须网络帮助。区间分块能实现的前提是前车加速度这一状态虽然无限,但是在状态空间中均匀分布,所以离散的区间块代表了一定大小的无限,如果状态空间中的状态并不均匀分布,就无法使用区间分块方法。但在汽车刹车问题上,区间分块方法仍具有泛用性。受限于实际情况,算法未能在真实车辆中进行测试,未来计划进一步实际研究。
参考文献:
[1]桂晶晶,吴芯洋,曾月,等.我国智能汽车发展现状及前景[J].中国高新科技,2022(4):60-61.(Gui Jingjing,Wu Xinyang,Zeng Yue,et al.Status and prospect of the development of smart cars in China[J].China High and New Technology,2022(4):60-61.)
[2]赵子骏,段希冉.智能汽车安全风险分析与应对路径[J].中国电子科学研究院学报,2022,17(8):822-827.(Zhao Zijun,Duan Xiran.Analysis of intelligent vehicle safety risks and their countermea-sures[J].Journal of China Academy of Electronics and Information Technology,2022,17(8):822-827.)
[3]肖凌云,胡文浩.智能汽车事故分析与安全应对策略研究[J].人工智能,2022(4):88-96.(Xiao Lingyun,Hu Wenhao.Research on intelligent vehicle accident analysis and safety response strategies[J].AI-View,2022(4):88-96.)
[4]李百明.汽车追尾预警系统设计[J].机电技术,2015(6):126-127,137.(Li Baiming.Design of automobile rear end warning system[J].Mechanical & Electrical Technology,2015(6):126-127,137.)
[5]Mamat M ,Ghani M N.Fuzzy logic controller on automated car braking system[C]//Proc of IEEE International Conference on Control and Automation.Piscataway,NJ:IEEE Press,2009:2371-2375.
[6]Ariyanto M,Haryadi D G,Munadi M,et al.Development of low-cost autonomous emergency braking system for an electric car[C]//Proc of the 5th International Conference on Electric Vehicular Technology.Piscataway,NJ:IEEE Press,2018:167-171.
[7]黃志芳,宋世杰,陈泽锐,等.汽车智能防撞系统[J].物联网技术,2020,10(5):67-69.(Huang Zhifang,Song Shijie,Chen Zerui,et al.Intelligent collision prevention system for automobiles[J].Internet of Things Technologies,2020,10(5):67-69.)
[8]黄志清,曲志伟,张吉,等.基于深度强化学习的端到端无人驾驶决策[J].电子学报,2020,48(9):1711-1719.(Huang Zhiqing,Qu Zhiwei,Zhang Ji,et al.End-to-end autonomous driving decision based on deep reinforcement learning[J].Acta Electronica Sinica,2020,48(9):1711-1719.)
[9]Silver D,Huang A,Maddison C J,et al.Mastering the game of go with deep neural networks and tree search[J].Nature,2016,529(7587):484.
[10]Sutton R S,Barto A G.Reinforcement learning:an introduction[M].2nd ed.Cambridge,CA:MIT Press,2018.
[11]王扬,陈智斌,吴兆蕊,等.强化学习求解组合最优化问题的研究综述[J].计算机科学与探索,2022,16(2):261-279.(Wang Yang,Chen Zhibin,Wu Zhaorui,et al.Review of reinforcement lear-ning for combinatorial optimization problem[J].Journal of Frontiers of Computer Science and Technology,2022,16(2):261-279.)
[12]Richter J D,Calix A R.Using double deep Q-learning to learn attitude control of fixed-wing aircraft[C]//Proc of the 16th International Conference on Signal-Image Technology & Internet-Based Systems.Pisca-taway,NJ:IEEE Press,2022:646-651.
[13]尹燕莉,张鑫新,潘小亮,等.基于等效因子的Q学习燃料电池汽车能量管理策略[J].汽车安全与节能学报,2022,13(4):785-795.(Yin Yanli,Zhang Xinxin,Pan Xiaoliang,et al.Equivalent factor of energy management strategy for fuel cell hybrid electric vehicles based on Q-learning[J].Journal of Automotive Safety and Energy,2022,13(4):785-795.)
[14]Qu Hong,Wei Xiaolong,Sun Chuhan,et al.Research on UAV air combat maneuver decision-making based on improved Q-learning algorithm[C]// Proc of the 5th IEEE International Conference on Information Systems and Computer Aided Education.Piscataway,NJ:IEEE Press,2022:55-58.
[15]Wu Zhaohui,Liu Yanfei,Pan Gang.A smart car control model for brake comfort based on car following[C]//Proc of IEEE Conference on Intelligent Transportation Systems.Piscataway,NJ:IEEE Press,2009:42-46.
[16]杜康豪,宋睿卓,魏慶来.强化学习在机器博弈上的应用综述[J].控制工程,2021,28(10):1998-2004.(Du Kanghao,Song Ruizhuo,Wei Qinglai.Review of reinforcement learning applications in machine games[J].Control Engineering of China,2021,28(10):1998-2004.)
[17]Lyu Le,Shen Yang,Zhang Sicheng.The advance of reinforcement learning and deep reinforcement learning[C]//Proc of IEEE International Conference on Electrical Engineering,Big Data and Algorithms.Piscataway,NJ:IEEE Press,2022:644-648.
[18]Janeway N R.Vehicle vibration limits to fit the passenger[J].SAE J,1948,56(8):48-49.
(上接第182页)
[12]Diehl P U,Pedroni B U,Cassidy A,et al.TrueHappiness:neuromorphic emotion recognition on TrueNorth[C]//Proc of International Joint Conference on Neural Networks.Piscataway,NJ:IEEE Press,2016:4278-4285.
[13]Han Bing,Srinivasan G,Roy K.RMP-SNN:residual membrane potential neuron for enabling deeper high-accuracy and low-latency spiking neural network[C]//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE Press,2020:13558-13567.
[14]Sengupta A,Ye Yuting,Wang R, et al.Going deeper in spiking neural networks:VGG and residual architectures[J].Frontiers in Neuroscience,2019,13.https://doi.org/10.3389/fnins.2019.00095.
[15]Kim S,Park S,Na B,et al.Spiking-YOLO:spiking neural network for energy-efficient object detection[C]//Proc of the 34th AAAI Confe-rence on Artificial Intelligence.Palo Alto,CA:AAAI Press,2020:11270-11277.
[16]Ding Jianhao,Yu Zhaofei,Tian Yonghong,et al.Optimal ANN-SNN conversion for fast and accurate inference in deep spiking neural networks[C]//Proc of the 30th International Joint Conference on Artificial Intelligence.Palo Alto,CA:AAAI Press,2021:2328-2336.
[17]Li Yuhang,Deng Shikuang,Dong Xin,et al.A free lunch from ANN:towards efficient,accurate spiking neural networks calibration[C]//Proc of the 38th International Conference on Machine Learning.2021:6316-6325.
[18]Bu Tong,Fang Wei,Ding Jianhao,et al.Optimal ANN-SNN conversion for high-accuracy and ultra-low-latency spiking neural networks[C]//Proc of International Conference on Learning Representations.2022:1-19.
[19]Cubuk E D,Zoph B,Mane D,et al.AutoAugment:learning augmentation strategies from data[C]//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE Press,2019:113-123.
[20]George M,Roger M.MIT-BIH arrhythmia database[DB/OL].(2005-02-24)[2023-07-15].https://www.physionet.org/content/mitdb/1.0.0/-31.
[21]張驰,唐凤珍.基于自适应编码的脉冲神经网络[J].计算机应用研究,2022,39(2):593-597.(Zhang Chi,Tang Fengzhen.Self-adaptive coding for spiking neural network[J].Application Research of Computers,2022,39(2):593-597.)
[22]Rathi N,Roy K.DIET-SNN:a low-latency spiking neural network with direct input encoding and leakage and threshold optimization[J].IEEE Trans on Neural Networks and Learning Systems,2023,34(6):3174- 3182.
[23]Horowitz M.1.1 computings energy problem(and what we can do about it)[C]// Proc of IEEE International Solid-State Circuits Conference Digest of Technical Papers.Piscataway,NJ:IEEE Press,2014:10-14.
[24]Deng Shikuang,Gu Shi.Optimal conversion of conventional artificial neural networks to spiking neural networks[C]//Proc of International Conference on Learning Representations.2021:1-14.
[25]Yan Zhanglu,Zhou Jun,Wong W F.Near lossless transfer learning for spiking neural networks[C]//Proc of the 35th AAAI Conference on Artificial Intelligence.Palo Alto,CA:AAAI Press,2021:10577-10584.
