HHUIM:一种新的启发式高效用项集挖掘方法
2024-02-18高智慧韩萌李昂刘淑娟穆栋梁
高智慧 韩萌 李昂 刘淑娟 穆栋梁
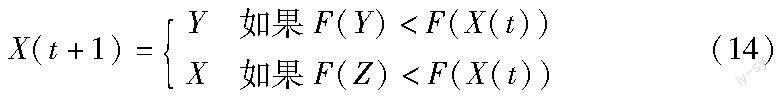
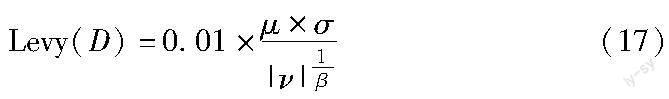
摘 要:针对基于启发式的高效用项集挖掘算法在挖掘过程中可能丢失大量项集的问题,提出一种新的启发式高效用项集挖掘算法HHUIM。HHUIM利用哈里斯鹰优化算法进行种群更新,能够有效减少项集丢失。提出并设计了鹰的替换策略,解决了搜索空间较大的问题,降低了适应度函数值低于最小效用阈值的鹰的数量。此外,提出存储回溯策略,可有效防止算法因收敛过快陷入局部最优。大量的实验表明,所提算法优于目前最先进的启发式高效用项集挖掘算法。
关键词:哈里斯鹰优化算法; 高效用项集挖掘; 启发式算法; 智能优化算法
中图分类号:TP311 文献标志码:A 文章编号:1001-3695(2024)01-015-0094-08
doi:10.19734/j.issn.1001-3695.2023.05.0198
HHUIM: new heuristic high utility itemset mining method
Abstract:In response to the problem of potentially losing a large number of itemsets during the mining process of heuristic-based high utility itemset mining algorithms, this paper proposed a new heuristic-based high utility itemset mining algorithm, called HHUIM. HHUIM utilized the Harris hawk optimization algorithm for population update, effectively reducing the loss of itemsets. This paper also introduced and designed a hawk replacement strategy to solve the problem of a large search space by decreasing the number of hawks with fitness values below the minimum utility threshold. Furthermore, this paper proposed a storage backtracking strategy to prevent premature convergence to local optima. Extensive experiments demonstrate that the proposed algorithm outperforms the state-of-the-art heuristic-based high utility itemset mining algorithms.
Key words:Harris eagle optimization algorithm; high utility itemset mining; heuristics; intelligent optimization algorithms
0 引言
高效用项集挖掘(HUIM)是数据挖掘领域中的一个重要课题[1],并受到广泛关注。已经提出了许多确定性的算法来有效地挖掘高效用项集(high utility itemsets,HUIs)[2~5],然而这些算法的性能会随着数据集的增大以及不同项总数的增大而降低[6,7]。此外,高效用项集往往分散在搜索空间中,这就要求传统的确定性算法要花费许多时间和空间来判断大量的候选项集是否为高效用项集。而启发式算法具有解决复杂、线性和高度非线性问题的能力,可以探索大型问题空间,根据适应度函数找到最优或接近最优的解决方案。因此,启发式算法与高效用项集挖掘的结合可以很好地解决上述问题,即可以在较短的时间内快速找到很多的HUIs。
Kannimuthu等人[8]将遗传算法(genetic algorithm,GA)应用于HUIM,提出需要指定最小效用阈值的HUPEUMU-GARM算法和不需要指定最小效用阈值的HUPEWUMU-GARM算法,这是启发式算法在高效用项集挖掘中的首次应用,能够在指数搜索空间中快速有效地挖掘HUIs,但是会丢失大量的项集。与基于GA的HUIM方法相比,基于粒子群优化(particle swarm optimization,PSO)的技术需要的参数更少[9],无须多次实验以找到合理的交叉和变异率,可以很容易实现[10]。Lin等人[11]首次将PSO应用于HUIM,在粒子更新过程中采用sigmoid函数,并开发了OR/NOR-tree结构,通过早期修剪粒子的无效组合来避免数据库的多次扫描。但由于限制了搜索空间,导致种群的多样性降低,会造成项集的大量丢失。Song等人[12]从人工蜂群(artificial bee colony,ABC)算法的角度对HUIM问题进行建模,利用位图进行信息表示和搜索空间剪枝,加速了HUIs的发现。Song等人[13]从人工鱼群(artificial fish swarm,AF)算法的角度研究了HUIs挖掘问题,并提出一种名为HUIM-AF的高效用项集挖掘算法。Pazhaniraja等人[14]提出一种基于灰狼优化和海豚回声定位优化的方法DE-BGWO来寻找高效用项集。此外,启发式算法还可以用于挖掘高效用项集的复杂模式,例如:Song等人[15]提出了基于标准PSO方法的HAUI-PSO算法来挖掘高平均效用项集(high average utility itemsets,HAUI);Pramanik等人[16]提出了挖掘CHUI-AC方法,首次使用自启发的蚁群算法挖掘闭合高效用项集(closed high utility itemsets,CHUIs);Lin等人[17]提出了一种基于GA的算法DcGA,在有限的时间内高效地挖掘CHUIs;Song等人[18]提出了基于交叉熵的算法TKU-CE+,用于啟发式地挖掘top-k高效用项集;Luna等人[19]提出用于挖掘top-k高效用项集的TKHUIM-GA算法,通过考虑每个项的效用来生成初始解,并相应地组合解决方案来指导搜索过程,可以减少运行时间和内存。
所有的这些算法都能够在较短的时间内快速找到很多高效用项集。然而这些算法因智能优化算法具有较强的随机性,或者由于其算法本身的特性很容易达到局部最优而不会继续探索下去,从而丢失一定的项集。比如基于遗传算法的HUIM具有交叉率和突变率,这是种群保持多样性的关键,而同时也会给算法带来一定的随机性,因此设置一个合适的突变率和交叉率是十分重要的,若设置不当,很容易导致算法陷入局部最优,进而导致算法不能继续挖掘出新的HUI。基于粒子群的算法在进行粒子的初始化时,要随机初始化粒子的速度以及位置,进行种群更新时,会根据轮盘赌选择法或者基于sigmoid函数,然而这两种算法都具有随机性。同样地,蝙蝠、人工蜂群、人工鱼群等群智能算法同粒子群一样,在种群初始化以及进行种群更新时,都具有随机性,因此会遗漏一定数量的高效用项集。所以,基于智能优化算法的HUIM在所有数据集中以及所有的阈值下,在一定的迭代次数内都能找到所有的高效用项集是十分困难且没有必要的。因此,怎样减少项集的丢失是一个研究重点。
值得注意的是,遗传算法、粒子群优化算法、蚁群算法、人工鱼群算法、人工蜂群算法等启发式算法对初始解的选择非常敏感。不同的初始解可能导致不同的搜索轨迹和最终结果。如果初始解选择不当,可能会导致算法陷入局部最优解或搜索效率低下。而哈里斯鹰优化算法(HHO)[20]对初始解的选择相对不敏感,能够处理不同类型的问题,并且对问题空间中的噪声和不确定性具有一定的鲁棒性,这使得它在处理高效用项集挖掘问题中表现良好。其次,由于遗传算法的强项是全局搜索,对于问题的局部优化可能相对较弱。遗传算法通过种群的多样性来探索解空间,但在确定局部最优解时可能需要更多的迭代和调整。人工鱼群算法在局部搜索中表现良好,通过觅食和尾随行为进行局部搜索;然而,在全局优化方面,算法可能受到限制,并且可能需要更多的迭代和调整才能找到全局最优解。而HHO具有探索性强、收敛性能好的优点,能够在较少的迭代次数内快速寻找最优解或近似最优解,是高效用项集挖掘问题的一个较优选择。
本文提出基于哈里斯鹰优化的高效用项集挖掘算法HHUIM(Harris hawks optimization-based high utility itemsets mi-ning)。为了有效表示项集的超集形成,本文提出并设计了基于位图的项集扩展策略。其次,为了解决搜索空间较大的问题,提出了鹰的替换策略,降低了适应度函数值低于最小效用阈值的鹰的数量。此外,为了防止算法因收敛过快陷入局部最优,提出存储回溯策略。
本文的主要贡献如下:a)首次提出基于哈里斯鹰优化的高效用项集挖掘方法HUIM-HHO,能够在较少的迭代次数内快速挖掘出较多的结果集;b)本文研究并设计了基于位图的项集扩展策略,基于此提出鹰的替换策略,有效缩减了搜索空间;c)为了避免算法因收敛过快陷入局部最优,本文提出存储回溯策略,保持了种群的多样性;d)在密集数据集和稀疏数据集中进行了大量的对比实验,结果表明,本文算法在时空效率、所挖掘出来的高效用项集的数量等方面优于目前最先进的算法。
1 基本概念
1.1 高效用项集挖掘基本概念
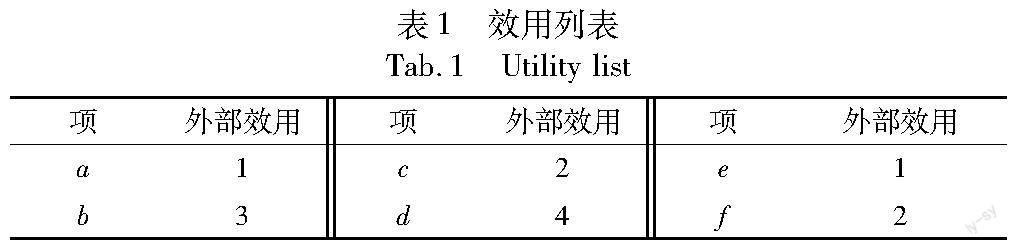
本节介绍高效用项集挖掘的相关定义。令I={i1,i2,i3,…,in}是由一组项组成的集合,令DB是一个数据库,这个数据库中有一个效用列表(表1)和一个事务列表(表2)。效用列表中的每个项I都有一个效用值。事务列表中的每个事务T都有一个唯一的标识符tid,且T是I的一个子集,其中每个项都与一个计数值相关联[21]。若一个项集是I的子集,且包含k个项,则称之为k-项集[22]。
定义1[2] 项i的外部效用(external utility),表示为eu(i),是DB效用表中i的效用值。例如,在表1中,项a的外部效用eu(a)=1。
定义2[2] 事务T中项i的内部效用(internal utility),表示为iu(i,T),是DB的事务表中与T中i相关联的计数值。例如,在表2中,事务T1中项a的内部效用iu(a,T1)=4。
定义3[3] 事务T中项i的效用,表示为u(i,T),是项i在事务T中的内部效用与项i的外部效用的乘积,即iu(i,T)和eu(i)的乘积,被定义为
u(i,T)=iu(i,T)×eu(i)(1)
例如,事务T1中项a的效用,计算为u(a,T1)=iu(a,T1)×eu(a)=4×1=4。
定义4[3] 事务T中项集X的效用,表示为u(X,T),是项集X中所有项的效用之和,其中X包含于T,被定义为
例如,事务T1中项集{a,b}的效用,u({a,b},T1)=u(a,T1)+u(b,T1)=4×1+4×3=16。事务T3中项集{a,b}的效用,u({a,b},T3)=u(a,T3)+u(b,T3)=2×1+1×3=5。
定義5[4] 项集X的效用,表示为u(X),是数据库DB中所有包含X的事务T中项集X的效用之和,被定义为
例如,项集{a,b}的效用为其在事务T1中的效用加上{a,b}在事务T3中的效用,即u({a,b})=u({a,b},T1)+u({a,b},T3)=16+5=21。
定义6[4] 事务T的效用(utility of transaction),表示为tu(T),是T中所有项的效用之和,其中,数据库DB的总效用是DB中所有事务的效用之和,被定义为
表2的最右列显示了每个事务的效用,例如,tu(T1)=u(a,T1)+u(b,T1)+u(d,T1)=4×1+4×3+3×4=28。表2中数据库的总效用为所有事务效用之和,即tu(T1)+tu(T2)+tu(T3)+tu(T4)=28+23+27+23=101。如果u(X)不小于用户指定的最小效用阈值(用minutil表示),或者不小于阈值δ(如果δ是一个百分比)与被挖掘数据库的总效用的乘积,则项集X是高效用项集[2]。给定一个数据库和一个最小效用阈值minutil,高效用项集挖掘问题是从数据库中发现效用不小于minutil的项集[5]。
定义7[2] DB中项集X的事务加权效用(transaction weighted utility),表示为twu(X),是数据库DB中包含项集X的所有事务的效用之和,定义为
例如,项集{a}的事务加权效用被计算为twu({a})=tu(T1)+tu(T3)=28+27=55。数据库中所有1-项集的twu如表3所示。
定义8[23] 若在数据库DB中,项集X的事务加权效用不小于minutil,则项集X是高事务加权效用项集(high transaction weighted utilization itemset,HTWUI)。
定义9[23] 若在数据库DB中,项集X的事务加权效用小于minutil,则项集X是低事务加权效用项集(low transaction weighted utilization itemset,LTWUI)。
例如,若minutil=50,則数据库DB中的1-HTWUI一共有5个,分别为{a},{b},{c},{d},{f},而1-LTWUI仅有{e}。
1.2 哈里斯鹰优化算法
在HHO中,候选解由鹰来表示,最优解(或近似最优解)被称之为猎物。HHO分为探索阶段和开发阶段,其中在开发阶段,鹰根据猎物的逃逸能量来改变自己的行为。猎物的逃逸能量E如式(6)所示。
其中:t是当前的迭代次数;T是最大的迭代次数;E0是猎物的初始逃逸能量(由式(7)可得);r是[0, 1]的随机数。
1)探索阶段
在探索阶段,鹰的位置通过式(8)进行更新。其中:X是鹰的位置;Xk是随机选择的一只鹰的位置;Xr是猎物的位置(全局最优解gbest);ub和lb是搜索空间的上界和下界;r1、r2、r3、r4以及q是五个[0,1]的随机数。Xm是当前鹰群的平均位置,可以用式(9)来计算。Xn是鹰群的第n只鹰,Num是鹰的个数(种群大小)。
2)开发阶段
a)软围攻状态。当r≥0.5且|E|<0.5时,进入软围攻状态,利用式(10)更新鹰的位置。其中,ΔX是猎物和当前鹰之间的距离,J是跳跃能量,计算如式(11)(12)所示。r5是每次迭代产生的[0,1]随机数。
X(t+1)=ΔX(t)-E|JXr(t)-X(t)|(10)
ΔX(t)=Xr(t)-X(t)(11)
J=2(1-r5)(12)
b)硬围攻状态。当r≥0.5且|E|<0.5时,进入硬围攻状态。在此状态下,通过式(13)进行鹰位置的更新。
X(t+1)=Xr(t)-E|ΔX(t)|(13)
c)渐进式快速俯冲的软包围。当r < 0.5且|E| ≥ 0.5时,执行渐进式快速俯冲的软包围,鹰的位置通过式(14)进行更新。
其中:F(·)为适应度函数;Y和Z为新生成的两只鹰,分别由式(15)(16)所得。式(16)中:D表示鹰的维度;α是一个D维的随机向量;Levy是莱维飞行函数(式(17))。
Y=Xr(t)-E|JXr(t)-X(t)|(15)
Z=Y+α×Levy(D)(16)
其中:μ、 ν是由正态分布生成的两个独立随机数;σ定义为式(18);β为常量,设置为1.5。
d)渐进式快速俯冲硬包围。当r<0.5且|E|<0.5时,HHO执行渐进式快速俯冲硬包围。在此状态,利用式(19)进行鹰的位置更新。
其中:F(·)为适应度函数;Y和Z分别是最近生成的两只鹰,分别由式(20)(21)所得。
Y=Xr(t)-E|JXr(t)-Xm(t)|(20)
Z=Y+α×Levy(D)(21)
Too等人[24]提出了二进制哈里斯鹰优化算法BHHO用于特征选择。第t次迭代时,第i只鹰的第d维度的位置是Xdi(t),利用HHO得到的t+1次迭代时的位置为ΔXdi(t+1),此时ΔXdi(t+1)为连续变量,BHHO利用式(22)(23)将连续变量转换为布尔变量。
2 HHUIM算法
与许多基于智能优化的HUIM类似,本文算法HHUIM是一种迭代算法,在每次迭代中产生大量的项集,并且通过计算项集所对应个体的适应度函数值来判断其是否为HUIs。
2.1 基于位图的项集扩展策略
HHUIM使用位图进行编码。如图1所示,每一只鹰用一个向量来表示。鹰的总长度为数据库中1-HTWUI的数量。以表2中的数据库为例,假设最小效用阈值为50,则1-HTWUI一共有5个,分别为{a},{b},{c},{d},{f}。鹰的每一个维度分别代表一个独立的项,若鹰的第i个位置设置为1,说明第i个项被选择组成一个项集,否则说明该项未被选择。如图1所示的向量X1=〈10100〉表示项集{a,c}。此外,表2中的数据库可以转换为图2的位图形式。
HHUIM使用位图来编码项集,项集X被表示为一个二进制的向量。假设向量最后一个1的后面有num0个0,随机选择k个0使其变为1,得到的新向量所对应的项集即为项集X的超集,其中k不大于num0。例如,图3为项集{a,c}的超集形成过程。项集{a,c}用向量可以表示为〈10100〉,最后的1在第3位,其后有两个0。若将第一个0变成1,此时向量变为〈10110〉,代表超集{a,c,d};若将最后一个0变成1,则向量变为〈10101〉,代表项集{a,c,f};若将项集{a,c,d}所对应向量的最后一个0变成1,形成〈10111〉,代表超集{a,c,d,f}。
2.2 鹰的替换策略
因启发式算法的随机性,出现在挖掘过程中的鹰hawki有可能是有效鹰也有可能是无效鹰,即hawki的适应度函数值可能大于minutil也可能小于minutil。因此本文提出鹰的替换策略,以缩小算法的搜索空间,加快算法的收敛,从而增加获得HUIs的概率,使算法以更少的迭代次数挖掘出较多的HUIs。在介绍鹰的替换策略之前,先进行一些定义。
定义10 鹰hawki的适应度函数值为其所对应项集Xi的效用值,记为fitness(hawki),定义为
fitness(hawki)=u(Xi)(24)
例如,如表2所示的数据集,假设鹰hawk3=〈110000〉,其所对应的项集为{a,b},则鹰hawk3的适应度函数值fitness(hawk3)=u({a,b})=21。
定义11 记鹰hawki所对应的位图为Biti,若鹰hawkk的位图满足式(25),则被称为鹰hawki的相反鹰,记为rehawki。
其中:Bitkj为鹰hawkk位图的第j维;temp为Biti的最后一个1所在的位置。例如,若鹰hawk1的位图为〈10100〉,则其相反鹰为〈00011〉。
定义12 鹰的局部突变(hawk local mutations)。在鷹的位图向量的第1到第temp个位置,随机选择1个位置进行比特变换,即将此位置的0变成1,或将此位置的1变为0。
定义13 鹰的超突变(hawk hypermutation)。在鹰的位图向量的第temp+1到第L个位置,随机选择k个位置进行比特变换,即此位置的0变成1,或将此位置的1变为0。其中1 鹰的替换策略伪代码如算法1所示。在算法运行的过程中,会判断当前hawki是否为有效鹰(步骤a))。若当前hawki的适应度函数值不小于minutil,则为有效鹰,将其所对应的项集输出为HUIs(步骤b))。若hawki为无效鹰,此时进入鹰的替换策略(步骤c)~j))。首先形成hawki的相反鹰rehawki(步骤d))。判断hawki的适应度函数值加上其相反鹰的适应度函数值是否大于minutil(步骤e))。若不小于minutil,则进行鹰的超突变,形成新的鹰hawki+1来替换鹰hawki(步骤f))。若小于minutil,则进行鹰的局部突变,形成新的鹰hawki+1来替换鹰hawki(步骤g)h))。 算法1 鹰的替换策略 输入:鹰hawki。 输出:新的鹰hawki+1。 a) if fitness(hawki)≥minutil b) SHUI←hawki+1所对应的项集 c) else if fitness(hawki) d) 形成hawki+1的相反鹰rehawki+1 e) if fitness(hawki)+fitness(rehawki)≥minutil f) 进行鹰的超突变,形成鹰hawki+1 g) else if fitness(hawki)+fitness(rehawki) h) 算法进行鹰的局部突变,形成鹰hawki+1 i) end if j) end if 例如,假设当前鹰hawki的位图向量为〈10100〉,图4显示了鹰的替换过程。首先计算hawki的适应度函数值fitness(hawki),若fitness(hawki)≥minutil,则将其所对应的项集输出为HUIs。若fitness(hawki) 2.3 存储回溯策略 为了防止算法因收敛过快容易陷入局部最优,提出存储回溯策略,以保持种群的多样性,使算法能够挖掘更多的HUIs。如图5所示,横坐标表示迭代次数,纵坐标表示所挖掘的高效用项集的数量,实线表示HUIs的数量随着迭代次数而变化的趋势。可以看出,HUIs的数量随着算法的迭代逐渐收敛。P点为HUIs的数量增长速率最快的点,此时种群的多样性是最大的。将P点的鹰群放入存储池中。当某次迭代挖掘出的HUIs的数量较小时,到达Q点。此时鹰群的多样性较低,算法接近收敛。将Q点的鹰群替换为存储池中的鹰群,使算法跳出局部最优,沿着虚线继续运行。存储回溯策略的伪代码如算法2所示。 算法2 存储回溯策略 输入:鹰群populationt;存放HUIs的集合SHUI;上次迭代产生的HUIs数量lastHUI;本次迭代产生的HUIs数量ΔHUI;ΔHUI的最大值maxHUI;存放在存储池内的鹰群Pc;种群大小pop_size。 输出:新的鹰群hawki+1。 a)ΔHUI=SHUI.size()-lastHUI; b)lastHUI=SHUI.size(); c)if ΔHUI>maxHUI d) maxHUI=ΔHUI e) Pc←populationt //将此时的鹰群放入存储池中 f)else if ΔHUI g) populationt←Pc //用存储池中的鹰群替换当前种群 h) end if 2.4 算法描述 本文HHUIM的伪代码如算法3所示。该方法的输入为事务数据集DB、最小效用阈值minutil以及最大的迭代次数T。算法一共分为数据初始化部分、种群初始化部分、种群更新部分以及高效用项集的识别部分四个部分。 第一个部分是数据初始化部分,包括对数据库的扫描以及重组数据库。步骤a)扫描数据库,计算所有1-项集的twu,若1-项集的twu小于minutil,说明这是没有希望的项,其超集不可能是HUIs,因此将该项从数据库中删除。步骤b)将重组后的数据库转换为如图2所示的位图形式。 第二个部分是种群初始化部分(步骤d)),随机初始化Num只鹰。其中鹰的大小为原始数据库中1-HTWUL的数量。分别计算每只鹰的适应度函数值,若适应度函数值不小于minutil,说明这个鹰所对应的项集是HUI,则将其放入SHUI中,并寻找适应度函数最高的那只鹰,作为gbest。 第三部分为种群更新部分(步骤g)~t)),对于当前种群中的每一只鹰,利用哈里斯鹰优化算法进行位置更新,形成新的种群。 第四部分是高效用项集的识别部分。步骤u)对更新位置后的鹰计算其适应度函数值,若适应度函数值不小于minutil,说明当前鹰所对应的项集为HUI,则将其放入SHUI集合中。然后更新gbest,算法迭代继续进行,直到达到最大的迭代次数。最后输出SHUI中所有的高效用项集以及项集的个数。 算法3 HHUIM 输入:事务数据集DB;最小效用阈值minutil;最大的迭代次数T。 输出:一组高效用项集。 a) 扫描数据库DB,计算所有1-项集的twu,将所有的1-LTWUI从DB中删除。 b) 将数据库转换为位图的形式。 c) SHUI=null。 // 将存放HUIs的集合初始化为空 d) 种群初始化。 e) t=1 to T f) 对于当前种群中的每一只鹰hawk(i)。 g) 生成一个随机数r,分别使用式(7)(12)计算E0和J,利用式(6)更新能量E。 h) if (|E|≥1) i) 搜索阶段,利用式(8)(17)更新鹰的位置。 j) else if (|E|<1) k) if (r≥0.5且|E|≥0.5) l) 软围攻阶段,利用式(10)(22)更新鹰的位置。 m) else if (r≥0.5且|E|<0.5) n) 硬围攻阶段,使用式(13)(22)进行位置的更新。 o) else if (r<0.5且|E|≥0.5) p) 漸进式快速俯冲的软包围,使用式(14)(22)更新位置。 q) else if (r<0.5且|E|<0.5) r) 渐进式快速俯冲的硬包围。使用式(19)(22)更新位置。 s) end if t) end if u) if fitness(hawki)≥minutil v) SHUI←hawki所对应的项集。 w) end if x) 更新gbest。 y) 算法循环迭代,直到达到最大的迭代次数。 z) 输出所有的高效用项集。 2.5 举例说明 为了演示算法HHUIM的挖掘过程,本节将举例说明,以表2中数据库为示例,并假设用户定义的最小效用阈值minutil=31,种群大小为3,最大迭代次数为5。挖掘过程如图6所示。 首先进行数据的处理。数据集中1-项集有{a},{b},{c},{d},{e},{f},其twu分别为55,101,73,78,46,50,均大于31,因此该窗口内所有的1-项集均为1-HTWUI。与此同时,将数据集转换为位图的形式,其中位图的长度为数据集中1-HTWUI的数量,即为6。 随后进入利用哈里斯鹰优化挖掘高效用项集阶段,其迭代过程如图6所示。首先初始化种群,即随机生成3个长度为6的向量,代表种群中3只鹰的位置,分别为Hawk01〈000100〉、Hawk02〈101001〉、Hawk03〈111100〉。接下来以Hawk02为例说明鹰Hawk02如何通过哈里斯鹰优化更新为Hawk12。 在初始种群中,适应度函数值最高的鹰为Hawk01〈000100〉,所以将Hawk01视为全局最优,用Xr来表示,此时Xr=Hawk01=〈000100〉。首先计算猎物的初始逃逸能量E0、逃逸能量E以及跳跃能量J。假设随机数r=0.7,r5=0.3,则根据式(6)(7)和(12)可得 因为|E|=0.64<1,且r=0.7≤0.5,所以进入软围攻阶段。根据式(10)(11)可得 ΔX12=X(t+1)=ΔX(t)-E|JXr(t)-X(t)|=Xr(t)-X(t)-E|JXr(t)-X(t)|= 〈000100〉-〈101001〉-0.64|1.4〈000100〉-〈101001〉|= 〈-1.64,0,-1.64,0.104,0,-1.64〉 此时ΔX12=〈-1.64,0,-1.64,0.104,0,-1.64〉是连续变量,需要将其转换为布尔变量。根据式(23)可得 假设rand0=0.1,rand1=0.3,rand2=0.7,rand3=0.4,rand4=0.6,rand5=0.1,根据式(22)可得X12=〈110101〉,即Hawk12=〈110101〉。 以第一次迭代为例,对于新种群中的每一只鹰,计算其适应度函数值。鹰Hawk11〈010100〉,Hawk12〈110101〉,Hawk13〈001100〉的适应度函数值分别为52,21,30。其中fitness(Hawk11)=52>31,说明Hawk11对应的项集X11={b,d}为高效用项集,则将项集{b,d}存入SHUI中。第一次迭代结束后,此时所有的HUIs只有{b,d}。算法进行迭代时,每当鹰的位置更新后,都需要判断其适应度函数值是否大于minutil,如果大于,则将其所对应的项集输出为HUIs。当达到最大的迭代次数时,算法结束,此时的高效用项集有7个,分别为{b,d},{a,b,d},{b},{b,c},{b,c,f},{b,c,d}和{b,c,e}。 3 实验 本章从HUIs的数量、算法运行时间、内存等方面进行了大量的对比实验,将HHUIM与目前较为先进的启发式高效用项集挖掘算法HUIM-BPSO[11]、HUIM-SPSO[25]、Bio-HUIF-PSO[23]、HUIM-AF[13]、Bio-HUIF-BA[23]以及Bio-HUIF-GA[23]进行对比。实验运行环境为16.0 GB可用RAM,Intel Core-i5-1235U@1.30 GHz CPU以及Windows 11操作系统。其中对比实验的源码以及数据集均下载于SPMF平台。因为智能优化算法具有极强的随机性,导致结果的偏差很大,本章所有实验数据均为运行10次取平均得到。实验所使用的数据集为chess、connect、mushroom、accidents、foodmart以及retail,其参数如表4所示。为了测试所提出策略的有效性,将鹰的替换策略与存储回溯策略分别加入HHUIM中,命名为HHUIM-R和HHUIM-S,并将其作为对比实验与HHUIM一起比较。 启发式HUIM因其迭代次数由用户指定,具有可随时获得结果的优点;此外,种群大小对实验结果的影响也很大。因此启发式HUIM大多数比较的是在相同迭代次数和相同种群大小的前提下,算法的运行时间以及能够挖掘出来HUIs的数量。而传统确定性算法需等待算法全部运行结束后才可以获得结果,且挖掘的项集是全部的HUIs,因此确定性算法比较的是时空效率。启发式HUIM与确定性算法是没有可比性的,因此本章未将确定性算法作为对比算法。 哈里斯鹰优化算法的时间复杂度主要取决于种群初始化、适应度值的计算以及鹰的位置更新。在本文中,面向高效用项集挖掘问题,对于N只鹰,初始化的时间复杂度为O(N),計算适应度函数值并寻找最优解的时间复杂度为O(T×N),假设数据集中1-HTWUI的数量为D,最大迭代次数为T,则鹰进行位置更新的时间复杂度为O(T×N×D)。因此,在HUIM中,影响时间复杂度的主要参数为迭代次数、种群大小以及数据集中1-HTWUI的数量D。但是D对于每一个数据集是固定不变的,无法人工设置,因此,T和N越大,算法的运行时间越长。然而,若T和N过小,则会丢失大量的项集。因此,需要根据经验以及多次的实验和分析,找到最优的参数组合。表5为先前算法的参数设置。本文根据以往经验,利用二分法将种群大小设置为20~500,迭代次数设置为100~10 000。实验中,在算法的运行时间以及查全率之间进行权衡,得到最终参数为:种群大小100,最大迭代次数1 000。 图7展示了随着阈值变化,算法挖掘出来的HUIs数量变化趋势。可以看出,HUIs的数量与阈值大小成反比,且随着阈值的增加,各算法所挖掘出来的HUIs数量达到了接近的水平。在chess数据集中(图7(a)),HHUIM及其变体HHUIM-R和HHUIM-S能够挖掘出最多的HUIs,当阈值为27%时,所挖掘出来的HUIs的数量是HUIM-BPSO、HUIM-SPSO以及HUIM-AF的两倍多。同样地,在connect(图7(b))以及mushroom(图7(c))数据集中,本文算法同样能够挖掘出最多的HUIs。图7(d)是在accidents数据集中挖掘出来的HUIs的数量,值得注意的是,在12%的效用阈值下,各算法均未能挖掘出所有高效用项集。这是因为实验参数设置种群大小为100,最大迭代次数为1 000,当达到最大迭代次数时,部分算法尚未收敛。如果能延长最大迭代次数,所能挖掘出的HUIs数量将进一步增加。将1 000次作为最大迭代次数是因为启发式算法的HUIM具有可以随时停止的优点,所以取1 000次作为最大迭代次数是完全合理的,即使此时算法尚未收敛。在稀疏数据集中,算法HUIM-SPSO和HUIM-AF的执行时间超过20 h仍未获得结果,因此不在图中显示。在foodmart中(图7(e)),本文算法挖掘到的HUIs数量略少于算法Bio-HUIF-PSO和Bio-HUIF-BA,这是因为foodmart数据集的平均事务长度最短,而HHO具有探索性较强的特点,所以挖掘出来的HUIs数量可能会有所丢失。在retail数据集中(图7(f)),本文算法能够挖掘到最多的高HUIs。Bio-HUIF-PSO和Bio-HUIF-BA算法的表现则会随着minutil的减小而出现HUIs数量减少的趋势。这是因为在实验过程中,这两个算法往往会产生空值,即挖掘出的HUIs数量为0。即使有时它们能够挖掘到更多的HUIs,但求平均后仍会出现此类现象。此外,从图中可以看出,HHUIM-R以及HHUIM-S能够有效提高稀疏数据集中算法能够挖掘出来的HUIs的数量。 图8展示了各算法在不同数据集上的运行时间。在chess数据集中,HHUIM和HHUIM-S的运行时间远远小于其他对比算法,其中HUIM-AF的运行时间是其3.5倍。在connect和mushroom数据集中,HHUIM以及HHUIM-S的运行时间最短,其中HHUIM-S比HHUIM更快一些。在connect数据集中,除算法HUIM-SPSO外,HHUIM、HHUIM-S以及HHUIM-R的运行时间远小于其他对比算法。图8(e)(f)为两个稀疏数据集,其中在foodmart数据集中,算法HHUIM和HHUIM-S的运行时间在18 s左右,在retail数据集中,运行时间为41 s左右。算法HHUIM-R需花费大量时间进行鹰的替换策略,因此所花费的时间大于算法HHUIM和HHUIM-S。 图9展示了算法在不同数据集上的内存占用对比。图9(a)(b)分别为数据集chess和connect,其密度分别为49.33%和33.33%,是相对密集的数据。HHUIM-R所占用的内存明显小于HHUIM和HHUIM-S,这是因为鹰的替换策略中,若当前鹰的适应度函数值小于最小效用阈值,则不将其作为下一次迭代初始种群中的个体,而是进行替换,相当于对搜索空间进行了剪枝,所以鹰的替换策略可以有效减少内存的使用。未来,可以将鹰的替换策略扩展为种群中个体的替换,以在密集数据集中降低内存消耗。在mushroom数据集中,本文算法所占用的内存仍然是最少的,而在最大的数据集accidents中,所占用的内存相对较多。在稀疏数据集retail中,算法HHUIM-S的内存占用要小于算法HHUIM和HHUIM-R,这是因为数据集retail为极度稀疏的数据集,大部分搜索空间是未被搜索到的,鹰的存储回溯策略在保持种群多样性的同时,可以帮助算法存储并追踪已经访问过的搜索空间位置,从而有效减少内存的使用。 经过综合比较算法执行时间、内存以及所挖掘出来的HUIs的数量,本文算法在性能方面表现最佳。其中,鹰的替换策略和存储回溯策略是有效的,它们可以在一定程度上增加算法所能夠挖掘出来的HUIs的数量。此外,在密集型数据集上,鹰的替换策略能够有效减少内存的使用;而在稀疏数据集上,存储回溯策略能够有效降低内存的占用。需要注意的是,算法的性能受到数据集特征、参数配置等多方面因素的影响,所以使用时需要综合考虑不同因素的影响,并进行适当优化。 4 结束语 高效用项集挖掘旨在挖掘出事务数据库中具有重要意义的项集。近年来,启发式算法得到了快速发展和广泛应用,并成为许多复杂问题求解的有效策略。其中,启发式算法与HUIM的结合能够有效提高海量数据中高效用项集的挖掘效率,因此这也成为了一个新兴的研究方向。然而,目前基于启发式的HUIM存在着容易丢失大量项集的问题,因此本文提出了一种新的基于哈里斯鹰优化的启发式高效用项集挖掘算法HHUIM。此外,本文提出了鹰的替换策略,该策略可大大缩小算法的搜索空间,降低适应度函数值低于最小效用阈值的鹰的数量;同时,针对算法因多样性下降而导致的收敛过快和大量项集丢失问题,提出了存储回溯策略。 为了测试本文算法的性能,在真实数据集中进行大量的实验,结果表明,本文算法优于目前最先进的启发式高效用项集挖掘算法。同时,鹰的替换策略和存储回溯策略也能够有效提高算法所挖掘出来的HUIs的数量,鹰的替换策略在密集数据集中,以及存储回溯策略在稀疏数据集中均能够减少内存的使用。 未来,本研究组将继续开发更加高效的高效用项集挖掘算法,并对鹰的替换策略进行优化。 参考文献: [1]Lin J C W, Djenouri Y, Srivastava G, et al. Efficient evolutionary computation model of closed high-utility itemset mining[J].Applied Intelligence,2022,52(9):10604-10616. [2]Liu Mengchi, Qu Junfeng. Mining high utility itemsets without candidate generation[C]//Proc of the 21st ACM International Conference on Information and Knowledge Management.New York:ACM Press,2012:55-64. [3]Zida S, Fournier-Viger P, Lin J C W, et al. EFIM: a fast and memory efficient algorithm for high-utility itemset mining[J].Knowledge and Information Systems,2017,51(2):595-625. [4]Fournier-Viger P, Wu C W, Zida S, et al. FHM:faster high-utility itemset mining using estimated utility co-occurrence pruning[M]//Andreasen T, Christiansen H, Cubero J C, et al. Foundations of Intelligent Systems.Cham:Springer,2014:83-92. [5]Cheng Zaihe, Fang Wei, Shen Wei, et al. An efficient utility-list based high-utility itemset mining algorithm[J].Applied Intelligence,2023,53(6):6992-7006. [6]Nawaz M S, Fournier-Viger P, Yun U, et al. Mining high utility itemsets with hill climbing and simulated annealing[J].ACM Trans on Management Information System,2021,13(1):1-22. [7]Fang Wei, Li Chongyang, Zhang Qiang, et al. An efficient biobjective evolutionary algorithm for mining frequent and high utility itemsets[J].Applied Soft Computing,2023,140:110233. [8]Kannimuthu S, Premalatha K. Discovery of high utility itemsets using genetic algorithm with ranked mutation[J].Applied Artificial Intelligence,2014,28(4):337-359. [9]吳大飞,杨光永,樊康生,等.多策略融合的改进粒子群优化算法[J].计算机应用研究,2022,39(11):3358-3364.(Wu Dafei, Yang Guangyong, Fan Kangsheng, et al. Improved particle swarm optimization algorithm with multi-strategy fusion[J].Application Research of Computers,2022,39(11):3358-3364.) [10]Lin J C W, Yang Lu, Fournier-Viger P, et al. A binary PSO approach to mine high-utility itemsets[J].Soft Computing,2017,21:5103-5121. [11]Lin J C W, Yang Lu, Fournier-Viger P, et al. Mining high-utility itemsets based on particle swarm optimization[J].Engineering Applications of Artificial Intelligence,2016,55:320-330. [12]Song Wei, Huang Chaoming. Discovering high utility itemsets based on the artificial bee colony algorithm[M]//Phung D,Tseng V, Webb G, et al. Advances in Knowledge Discovery and Data Mining.Cham:Springer,2018:3-14. [13]Song Wei, Li Junya, Huang Chaoming. Artificial fish swarm algorithm for mining high utility itemsets[M]//Tan Ying, Shi Yuhui.Advances in Swarm Intelligence.Cham:Springer,2021:407-419. [14]Pazhaniraja N, Sountharrajan S, Suganya E, et al. Optimizing high-utility item mining using hybrid dolphin echolocation and Boolean grey wolf optimization[J].Journal of Ambient Intelligence and Huma-nized Computing,2023,14(3):2327-2339. [15]Song Wei, Huang Chaoming. Mining high average-utility itemsets based on particle swarm optimization[J].Data Science and Pattern Recognition,2020,4(2):19-32. [16]Pramanik S, Goswami A. Discovery of closed high utility itemsets using a fast nature-inspired ant colony algorithm[J].Applied Intelligence,2022,52(8):8839-8855. [17]Lin J C W, Djenouri Y, Srivastava G, et al. A predictive GA-based model for closed high-utility itemset mining[J].Applied Soft Computing,2021,108:107422. [18]Song Wei, Zheng Chuanlong, Huang Chaomin, et al. Heuristically mining the top-k high-utility itemsets with cross-entropy optimization[J].Applied Intelligence,2022,52:17026-17041. [19]Luna J M, Kiran R U, Fournier-Viger P, et al. Efficient mining of top-k high utility itemsets through genetic algorithms[J].Information Sciences,2023,624:529-553. [20]Heidari A A, Mirjalili S, Faris H, et al. Harris hawks optimization:algorithm and applications[J].Future Generation Computer Systems,2019,97:849-872. [21]孫蕊,韩萌,张春砚,等.精简高效用模式挖掘综述[J].计算机应用研究,2021,38(4):975-981.(Sun Rui, Han Meng, Zhang Chunyan, et al. Survey of algorithms for concise high utility pattern mining[J].Application Research of Computers,2021,38(4):975-981.) [22]张春砚,韩萌,孙蕊,等.高效用模式挖掘关键技术综述[J].计算机应用研究,2021,38(2):330-340.(Zhang Chunyan, Han Meng, Sun Rui. Survey of key technologies for high utility patterns mining[J].Application Research of Computers,2021,38(2):330-340.) [23]Song Wei, Huang Chaomin. Mining high utility itemsets using bio-inspired algorithms:a diverse optimal value framework[J].IEEE Access,2018,6:19568-19582. [24]Too J, Abdullah A R, Mohd Saad N. A new quadratic binary Harris hawk optimization for feature selection[J].Electronics,2019,8(10):1130. [25]Song Wei, Li Junya. Discovering high utility itemsets using set-based particle swarm optimization[M]//Yang Xiaochun, Wang Changdong, Islam M S, et al. Advanced Data Mining and Applications.Cham:Springer,2020:38-53. [26]Wu J M T, Zhan J, Lin J C W. An ACO-based approach to mine high-utility itemsets[J].Knowledge-Based Systems,2017,116:102-113. [27]Arunkumar M S, Suresh P, Gunavathi C. High utility infrequent itemset mining using a customized ant colony algorithm[J].International Journal of Parallel Programming,2020,48:833-849. [28]Pazhaniraja N, Sountharrajan S, Sathis Kumar B. High utility itemset mining: a Boolean operators-based modified grey wolf optimization algorithm[J].Soft Computing,2020,24:16691-16704.
