基于Spark和NRSCA策略的并行深度森林算法
2024-02-18毛伊敏刘绍芬
毛伊敏 刘绍芬
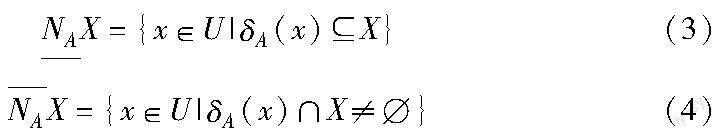
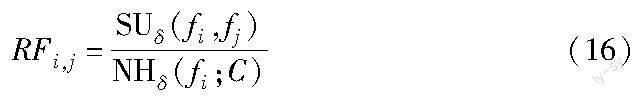
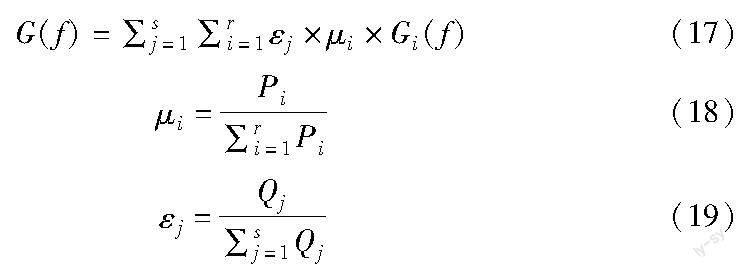
摘 要:針对并行深度森林在大数据环境下存在冗余及无关特征过多、两端特征利用率过低、模型收敛速度慢以及级联森林并行效率低等问题,提出了基于Spark和NRSCA策略的并行深度森林算法——PDF-SNRSCA。首先,该算法提出了基于邻域粗糙集和Fisher score的特征选择策略(FS-NRS),通过衡量特征的相关性和冗余度,对特征进行过滤,有效减少了冗余及无关特征的数量;其次,提出了一种随机选择和等距提取的扫描策略(S-RSEE),保证了所有特征能够同概率被利用,解决了多粒度扫描两端特征利用率低的问题;最后,结合Spark框架,实现级联森林并行化训练,提出了基于重要性指数的特征筛选机制(FFM-II),筛选出非关键性特征,平衡增强类向量与原始类向量维度,从而加快模型收敛速度,同时设计了基于SCA的任务调度机制(TSM-SCA),将任务重新分配,保证集群负载均衡,解决了级联森林并行效率低的问题。实验表明,PDF-SNRSCA算法能有效提高深度森林的分类效果,且对深度森林并行化训练的效率也有大幅提升。
关键词:并行深度森林算法; Spark框架; 邻域粗糙集; 正弦余弦算法; 多粒度扫描
中图分类号:TP181 文献标志码:A 文章编号:1001-3695(2024)01-019-0126-08
doi:10.19734/j.issn.1001-3695.2023.05.0196
Parallel deep forest algorithm based on Spark and NRSCA strategy
Abstract:Aiming to address several issues encountered by parallel deep forest algorithms in big data environments, such as excessive redundancy and irrelevant features, low utilization rate of features at both ends, slow model convergence speed, and low parallel efficiency of cascading forests, this paper proposed a parallel deep forest algorithm based on Spark and NRSCA strategy (PDF-SNRSCA). Firstly, the algorithm proposed a feature selection strategy (FS-NRS) based on neighborhood rough sets and Fisher score, which measured the correlation and redundancy of features to effectively reduce the number of redundant and irrelevant features. Secondly, it proposed a scanning strategy based on random selection and equidistant extraction (S-RSEE) to ensure that all features were utilized with the same probability and solved the problem of low utilization rate of two ends in multi-granularing scanning. Finally, combining with the Spark framework, the algorithm realized the parallel trai-ning of cascading forests, and it proposed a feature filtering mechanism based on the importance index (FFM-II) to balance the dimensions of enhanced class vectors and original class vectors, thereby accelerating the model convergence speed. Meanwhile, the algorithm designed a task scheduling mechanism based on SCA (TSM-SCA) to redistribute tasks and ensure load balancing in the cluster, which solved the problem of low parallel efficiency of cascading forests. Experiments show that the PDF-SNRSCA algorithm can effectively improve the classification performance of deep forests and greatly enhance the efficiency of parallel training of deep forests.
Key words:parallel deep forest algorithm; Spark framework; neighborhood rough sets; sine cosine algorithm; multi-granularing scanning
0 引言
深度森林[1]是基于森林的集成学习方法,其超参数较少,具有良好的表征学习能力,被广泛应用于图像识别[2,3]、故障诊断[4]、指标预测[5]等各个领域。然而随着大数据时代的到来,各个领域的数据量和特征量呈指数级增长,深度森林面对数据量和特征量的增长,其训练代价明显增加,训练效果下降。因此,改进深度森林训练模型,提高其并行化效率刻不容缓。
针对大数据规模庞大且计算复杂等问题,谷歌公司开发的Spark[6]计算速度快,通用性强,易于使用,并且支持多种语言,受到了广大学者的青睐。目前已有基于Spark框架的并行深度森林算法投入到实际应用当中。例如文献[7]在潜在客户离网预测系统中,提出了基于Spark的并行深度森林算法(pa-rallel deep forest algorithm based on Spark,PDFS),该算法提出了基于索引的多粒度扫描算法和随机采样构造随机森林的方法,以解决多粒度扫描阶段存储空间占用大的问题。文献[8]提出了一种基于并行深度森林的网络入侵检测算法(network intrusion detection algorithm based on parallel deep forest,NID-PDF),该算法使用效率排序和分区完整性检查的方式优化了RDD缓存替换策略,从而提高了并行作业效率。为了进一步提高并行深度森林的效率,文献[9]提出了基于Spark框架的并行深度森林算法(bag of little bootstraps-gcForset,BLB-gcForest),该算法使用了自助采样机制,减少了大量数据样本在级联森林层中的传输,并且提出自适应子森林划分算法,提高了各节点的利用率。以上三种改进的深度森林算法在分类效果和训练效率上相比原始深度森林算法有了一定的提升,但是仍存在以下不足:a)在特征选择阶段,没有对原始数据的特征进行有效划分和筛选,导致级联森林训练过程中存在冗余特征过多的问题;b)在多粒度扫描阶段,原始扫描方法采用滑动方式会导致两端特征利用率过低;c)在模型并行化训练阶段,原始类向量和增强类向量维度相差过大,使得增强类向量淹没在原始类向量中,导致模型收敛速度慢,并且任务调度不均衡将造成集群负载不均衡,级联森林并行化效率低下的情况。
针对以上问题,本文提出了基于邻域粗糙集改进的并行深度森林算法——PDF-SNRSCA,算法的主要工作如下:
a)在特征选择阶段,提出了基于邻域粗糙集和Fisher score的特征选择策略(feature selection strategy based on neighborhood rough sets and Fisher score,FS-NRS),通过衡量特征的相关性和冗余度,筛选出信息量较大的特征,解决冗余及无关特征过多的问题。
b)在多粒度扫描阶段,提出了一种随机选择和等距提取的扫描策略(scanning strategy for random selection and equidistant extraction,S-RSEE),替代原始的多粒度扫描策略,解决多粒度扫描两端特征利用率低的问题。
c)在模型并行化训练阶段,提出了基于重要性指数的特征筛选机制(feature filtering mechanism based on importance index,FFM-II),以此平衡增强类向量与原始类向量维度,解决了模型收敛速度慢的问题;同时设计了基于SCA的任务调度机制(task scheduling mechanism based on SCA,TSM-SCA),将任务重新分配,保证集群负载均衡,提高了级联森林并行化效率。
1 相关概念介绍
1.1 邻域粗糙集
邻域粗糙集[10]是粗糙集的邻域近似扩展,是在δ邻域的基础上建立基于距离度量函数的邻域关系,其研究对象是邻域信息系统。
定义1 邻域信息系统[11]。设一个数据样本集U={x1,x2,…,xn},其中F={f1,f2,…,fm}是它的特征属性集, C={c1,c2,…,ca}是它的标签属性集,则三者构成的系统NS=〈U,F,C〉即为邻域信息系统。
a)在NS=〈U,F,C〉中,对于任意样本xi,xj∈U,xi在IF下的邻域集可表示为
δI(xi)={xj∈U|disI(xi,xj)≤δ}(1)
其中:δI(xi)表示样本xi在特征子集I下,以δ大小为半径的邻域信息粒;dis为距离函数。样本xi和xj在属性fp∈I下的绝对距离可表示为
disI(xi,xj)=∑|I|i=1|H(xi,fp)-H(xj,fp)|(2)
其中:H(x,fp)为样本x在属性fp上的取值。
b)在NS=〈U,F,C〉中,令邻域半径为δ,特征子集IF在U上确定的邻域关系为NI,对于近似对象集XU关于NI的邻域下近似集和领域上近似集可分别表示为
定义2 邻域信息熵[12]。给定邻域信息系统NS=〈U,F,C〉,令邻域半径为δ,当f∈F,f的邻域信息熵定義为
其中:δf(xi)是样本xi根据属性f在U上的邻域关系计算得到的邻域集;NHδ(f)度量特征中信息量的大小,NHδ(f)越大,信息量越大。
定义3 邻域互信息[12]。给定邻域决策信息系统NS=〈U,F,C〉,令邻域半径为δ, 当f∈F, f与C的邻域互信息定义为
其中:δC(xi), δf(xi), δf∪C(xi)是样本xi根据属性集f;C在U上的邻域关系计算得到的邻域集;NHδ(f;C)度量特征与标签之间的相关性,NHδ(f;C)越大,特征与标签相关性越强。
定义4 邻域对称不确定性[13]。给定邻域决策信息系统NS=〈U,F,C〉,令邻域半径为δ,当f∈F,f与C的邻域不确定性定义为
其中:NHδ(f;C)表示f和C的邻域互信息;NHδ(f)表示f的邻域信息熵;NHδ(C)表示C的邻域信息熵;SUδ(f,C)度量特征与标签之间的相关性,SUδ(f,C)越大,特征与标签的相关性越强。
1.2 Fisher score
Fisher score[14]是通过衡量特征在同一类别和不同类别的取值差异来衡量特征的重要性,Fisher score的值越高,表明特征在不同类别之间的差异性越大,在同一类别中的差异性越小,特征越重要。假设有特征i和类别j,则其Fisher score FSi的定义为
其中:μij和ρij分别是特征i在类别j中的均值和方差;μi为特征i的均值;nj为类别j中的样本数。
1.3 正余弦算法
正余弦算法(sine cosine algorithm,SCA)[15]利用正弦函数和余弦函数的数学性质,通过自适应改变正弦函数和余弦函数的振幅来平衡算法在搜索过程中的全局探索和局部开发能力,并最终找到全局最优解。其主要步骤为:
a)初始化种群。初始化种群数量为M,Xi=(xi1,xi2,…,xiN)表示第i(i=1,2,…,M)个个体,个体的搜索空间维度为N,每个个体的初始位置为
xij=xmin,j+r(0,1)×(xmax,j-xmin,j)(9)
其中:xmax,j和xmin,j分别为个体在维度j上的上下限;r(0,1)为(0,1)内的随机量。
b)定义个体的适应度函数。当各节点的负载率与平均负载率方差最小时,表明达到均衡状态,因此,本文定义个体适应度函数如下:
其中:ηi表示节点Ni(i=1,2,…,n)当前的负载率;η0表示达到平衡时各节点的平均负载率。
c)更新个体位置。通过目标函数,计算个体的适应度,寻找全局最优解,最优解表示为Pg=(pg1,p2,…,pgN),并且迭代更新个体的位置,更新可通过下式计算得出
其中:xt+1ij为个体i在维度j上的更新位置; xtij为个体i在维度j上的原位置; pgj为当前全局最优解的j维位置;r2、r3和r4为三个服从均匀分布的随机数,r2∈[0,2π],r3∈[-2,2],r4∈[0,1];r1为振幅控制参数,其表达式为
d)种群迭代。重复步骤c),直到满足设定条件,输出全局最优的个体Pg。
2 PDF-SNRSCA算法
PDF-SNRSCA算法主要包含特征预处理、多粒度扫描、级联森林并行化训练三个阶段。a)特征预处理阶段提出FS-NRS策略,通过衡量特征的相关性和冗余度,过滤冗余及无关特征;b)多粒度扫描阶段设计S-RSEE策略,利用随机扫描和等距提取相结合的方法,使得特征同概率被选取,解决了两端特征利用率过低的问题;c)级联森林并行化训练阶段首先结合Spark框架搭建并行森都森林模型,提出FFM-II机制,通过模型的训练准确率计算特征的重要性指数,剔除非关键特征,平衡增强类向量与原始类向量维度,加快模型收敛速度;同时设计TSM-SCA机制,通过SCA算法来迭代寻找最优的调度方案,实现负载均衡,提高并行化效率。
2.1 特征预处理
针对原始特征集中冗余及无关特征过多的问题,提出了FS-NRS的特征选择策略,该策略主要包含两个步骤:
a)筛选无关特征。为了准确筛选出原始特征集中存在的大量无关特征,提出了特征分割参数FSP将原始特征集划分为无关特征集和候选特征集。其划分过程如下:首先计算出每个特征Fisher score FSf和SUδ(f,C);然后根据FSf和SUδ(f,C)计算原始特征集中每个特征的特征分割参数FSP,并且根据FSP的大小进行降序排序;最后按照FSP值,从高到低将原始特征集划分为候选特征集合和无关特征集合两部分。
定义5 特征分割参数FSP。已知样本集合中,类别数量为k,特征f的特征分割参数FSP为
FSP=FSfSUδ(f,C)(13)
其中
证明 根据邻域对称不确定性定义可知, SUδ(f,C)可以衡量当前特征f和标签集C的相关性,当SUδ(f,C)较大时,表明当前特征f和標签集C的相关性越大;根据Fisher score定义可知,FSf可以衡量特征f的重要性,FSf越大,表明特征f的重要性越高。FSP设定成邻域对称不确定性与Fisher score的乘积,同时考虑了特征相关性和特征重要性,当所选特征与标签具有高相关性且特征重要性越高时,FSP的值越大,重要特征被选出,因此可用FSP作为特征分割,证毕。
b)过滤冗余特征。经过无关特征的初步过滤后,候选特征集合依旧存在着大量的冗余特征,因此提出了冗余系数RF,对候选特征集进行过滤,进一步筛选出大量冗余特征,获取优质特征集。该过程如下:首先计算特征与标签间的邻域互信息NHδ(fi;C)以及特征间的邻域不确定性SUδ(fi,fj);然后利用NHδ(fi;C)和SUδ(fi,fj)计算特征间的冗余系数RF,并且根据冗余系数和阈值比较,进一步消除冗余特征,获取优质特征集。
定义6 冗余系数RF。已知存在特征fi、fj,则两个特征的冗余系数RFi,j为
证明 SUδ(fi,fj)为特征和特征之间的邻域对称不确定性,根据邻域对称不确定性可知,SUδ(fi,fj)可以度量特征和特征之间的相关性程度,SUδ(fi,fj)越大,表示特征与特征之间的相关性越大,特征间信息的冗余程度越大; NHδ(fi;C)为特征和标签之间的邻域互信息,根据邻域互信息可知,NHδ(fi;C)可以度量特征和标签之间的相关程度,NHδ(fi;C)越大,表示特征与标签之间的相关信息量越大。当SUδ(fi,fj)越大,NHδ(fi;C)越小时,表明特征fi、fj之间重叠的信息量越大,特征fi与标签C相关度越小,此时SUδ(fi,fj)/NHδ(fi;C)比值越大,特征之间存在巨大冗余,因此冗余系数RF可以衡量特征冗余信息量的大小,证毕。
算法1 FS-NMI策略
输入:样本集合U,标签集合C,特征集合F={f1,f2,…,fm},参数θ和η。
输出:特征子集L。
1) 筛选无关特征
//Q表示中间数据集合,用来暂时存储已计算FSP值的特征
Q=;
//θ表示划分的比例系数
determine the division ratio:θ;
for k=1 to m do
calculate FSfk for fk in the sample set;
calculate FSP=FSfkSUδ(fk,C)for in the sample set;
Q=Q+{fk}
end for
order Q in descending FSP value;
//根据θ将中间数据集合Q划分为无关特征集合和候选特征集合
divide the Q into two parts at the ratio θ:independent feature set,candidate feature set L;
output feature subset L;
2) 过滤冗余特征
//η表示阈值
defined threshold:η;
//fi表示第一候选特征
for fi∈L
calculate NHδ(fi;C);
//fj表示第二候选特征
for fj∈L-{fi}
calculate SUδ(fi,fj);
calculate RFi,j;
if RFi,j>η
L=L-{fj};
end for
end for
output feature subset L;
2.2 多粒度扫描
经过特征预处理阶段获取的优质特征集,被送入多粒度扫描阶段处理,然而传统多粒度扫描存在两端特征利用率过低的问题,为此提出S-RSEE的特征扫描策略。该策略具体流程如下:
a)随机扫描。特征预处理阶段得到特征集合L,其大小为x,类别数为y,从L中随机抽取h个特征组成一个特征片段,重复抽取b次,共生成b个特征片段,将每个特征片段导入到随机森林中训练,得到b个y维的类向量。
b)等距提取。将特征集合L等分为b个特征片段,每份大小为x/b」,将每个特征片段导入到完全随机森林中训练,同样得到b个y维的类向量。
c)初始化类向量。重复上述两个阶段z次,将z次训练后得到的类向量进行拼接,最后得到2zby维的原始类向量E。
算法2 S-RSEE策略
输入:特征子集L,子集大小为x,类别数为y,参数h、b、z。
输出:原始类向量E。
initialization parameters h,b,z;
/*h表示随机抽取特征的数量,b表示重复抽取的次数,z表示重复两个阶段的次数*/
define variable H,W,B1,B2;
/*H用来存储随机抽取的特征,W表示等距划分后,特征片段的大小,B1存储随机扫描训练后的类向量,B2存储等距提取训练后的类向量*/
for k=1 to z do
//随机扫描阶段
for i=1 to b do
randomly sample h features from the original feature set L;
combine feature h features into a feature segment H;
get one y-dim class vector from random forest (H);
end for
B1=B1 + Get b y-dim class vectors;
//等距提取階段
divide the feature set L equally into b parts, each of size W=x/b」;
for i=1 to B2 do
get one y-dim class vector from complete random forest (W);
end for
B2=B2+get b y-dim class vectors;
end for
//初始化类向量阶段
merge B1 and B2 into the original class vector E
2.3 级联森林并行化训练
针对并行训练过程中模型收敛速度慢、级联森林并行训练效率低的问题,本文结合Spark对每层级联森林模型进行并行化训练,该过程分为两个阶段:a)并行构建级联森林,利用Spark框架搭建并行深度森林,提出了FFM-II的特征筛选机制,根据级联森林训练得出的准确率剔除非关键特征,平衡增强类向量和原始类向量维度;b)负载均衡,设计了TSM-SCA的任务调度机制,利用SCA算法计算出最优的任务分配方案,然后Spark集群按照方案分配任务。
2.3.1 并行构建级联森林
在利用Spark构建并行级联森林过程中,由于级联森林训练得到的增强类向量维度远低于原始类向量维度,导致模型收敛速度慢,因此提出FFM-II的特征筛选机制,通过模型的训练准确率计算特征的重要性指数,以此剔除部分非关键特征,平衡增强类向量和原始类向量维度,从而加快模型收敛速度,该策略过程如下:
a)过滤特征。首先根据当前层级联森林的训练准确率,计算每个特征的重要性指数G(f),并根据G(f)的值对原始类向量中的特征从低到高排序;然后提出自适应比例系数QDF,按照当前原始类向量的特征数量计算自适应比例系数QDF;最后根据QDF值将排好序的原始类向量E分为非关键类向量和有效类向量,将非关键类向量放入到非關键类向量集合R。
b)合并类向量。首先拼接前面所有层级联森林训练得到的增强类向量,得到总的增强类向量D;然后将总的增强类向量D与下一层级联森林的原始类向量E′进行拼接;最后从拼接后的类向量中删除非关键类向量集合R中包含的特征,获取输入到下一层级联森林的类向量ED。
定义7 重要性指数G(f)。假设在当前层级森林中,决策树权重为μi,子森林权重为εj,特征f的重要性在第j个子森林的第i棵决策树中为Gi(f),则在当前层级联森林中,特征f重要性指数为
其中:Pi是第j个子森林中第i棵决策树的准确率;Qj是第j个子森林的准确率。
证明 假设每层级联森林中含有s个子森林,每个森林中含有r棵决策树,其中,第j个子森林中第i棵决策树的准确率为Pi,第j个子森林的准确率为Qj,准确率可以衡量决策树和子森林的分类能力。Pi与∑ri=1Pi的比值表示单个决策树预测准确率与子森林总准确率归一化权重,其值越大说明该决策树分类能力越强,在子森林中越重要。同理,Qj与∑sj=1Qj的比值反映了Qj在本层级联森林总准确率∑sj=1Qj的权重,其值越大则说明该子森林分类能力越强,在本层级联森林中越重要。Gi(f)表示特征f在第i棵决策树中的重要性,Gi(f)的值只能衡量特征在当前决策树中的重要性,若想要衡量特征f在当前层级联森林中的重要性,需要计算特征在当前层所有决策树中的重要程度,所以在当前层级联森林中,特征f重要性指数为
G(f)=∑sj=1∑ri=1εj×μi×Gi(f)(20)
定义8 自适应比例系数QDF。假设第λ层级联森林中,原始类向量的特征数量为Nλ,则第λ层的自适应比例系数QDF为
证明 当λ=1时,第1层级联森林原始向量的特征数量为Nλ,令QλDF=1/[2×(λ+1/log2Nλ)],此时QDF<0.25,则QλDF 综上QDF是一个可以根据级联森林的层数和特征数量来动态调整划分比例的系数,且级联森林的层数越多,划分比例越小。 算法3 FFM-II机制 输入:当前层的原始类向量E,下一层的原始类向量E′,前面所有层的增强类向量之和D,前面所有层的冗余类向量之和R;当前层的训练结果Pi和Qj。 输出:下一层类向量ED。 for i=1 to r do //计算决策树的权重 calculate weight μi=Pi/∑ri=1Pi for each decision tree; end for for j=1 to s do //计算子森林的权重 calculate εj=Qj/∑sj=1Qj for child forest; end for //计算特征的重要性指数 for j=1 to s do for i=1 to r do calculate the importance of each feature Gi(f) in each decision tree; Gj(f)=∑r-1i=1μi×Gi(f); end for G(f)=∑s-1j=1εj×Gj(f); end for order E in descending G(f) value; //QDF表示自适应比例系数 calculate the ratio QDF=1/[2×(λ+1/log2Nλ)] according to the number of features; divide the E into two parts at the ratio QDF:valid vectors E,redundant vectors R; //合并类向量 ED=E′+D-R; output ED; 2.3.2 负载均衡 针对Spark各节点计算能力偏差造成的集群负载不均衡,导致级联森林并行化效率低下的问题,设计了TSM-SCA的任务调度机制,通过SCA算法求解最优的调度方案,重新分配任务,使节点达到负载均衡的状态,从而提高并行化效率。具体步骤如下: a)初始化SCA种群。初始化种群数量为k,Xi=(xi1,xi2,…,xiN)表示第i(i=1,2,…,k)个个体,根据集群节点数量设置搜索空间维度为N。 b)更新个体的位置。提出基于惯性因子ω的位置更新函数W(x)来替代式(10),以此提升个体的全局搜索能力,加快算法收敛。 c)更新振幅控制参数r1。式(11)中r1是线性递减的,前期和后期递减速度相同,导致前期全局搜索不充分,后期算法无法快速收敛。为了获得更好的稳定性和更高的寻优能力,对控制参数r1提出一种基于正切函数的曲线自适应振幅调整策略,来保证解的优质性。 d)判断当前最优个体是否满足解条件。若满足条件或者设定的迭代次数达到上限,则输出当前最优个体Pg,不满足则重复b)c)。 e)任务分配。集群根据得到的任务调度方案Pg=(pg1,pg2,…,pgN)进行任务分配,实现集群的负载平衡。 定义9 位置更新函数W(x)。假设xtij为个体i在维度j上的原位置,xt+1ij为个体i在维度j上的更新位置,pgj为当前全局最优解的j维位置,ω(t)为惯性因子,位置更新函数为 其中:T为最大迭代次数;ωmax为初始惯性因子,即最大值;ωmin为迭代结束时的惯性因子,即最小值。 证明 根据惯性因子的迭代定理[15]可知,在迭代早期,较大惯性因子可以提升全局搜索能力,在迭代晚期,较小惯性因子可以增强局部开发能力,加速算法收敛。当前迭代次数t和最大迭代次数T的比值t/T表示当前迭代所处的时间段, t与T的比值在[0,1],因为函数f(t)=1-(t/T)2在t/T∈[0,1]先缓慢递减,后快速递减,且当t/T→0时,ω→ωmax,t/T→1时,ω→ωmin,所以惯性因子ω在早期取值较大,在后期取值较小,ω(t)满足了惯性因子的迭代定理。因此,使用W(t)可以提升全局搜索能力,加快算法收敛,证毕。 定义10 r1自适应振幅调整策略。假设T为最大迭代次数,a为常数,则在t次迭代时,控制参数r1为 证明 当前迭代次数t和最大迭代次数T的比值t/T表示当前迭代所处的时间段,t与T的比值在[0,1],因为函数f(t)=1-tan[(π/4)×(t/T)]在t/T∈[0,1]区间先缓慢递减,后快速递减,所以r1∈[0,a]的递减速率先慢后快。在前期r1递减缓慢,保证了前期的迭代次数比原始SCA算法更多,可以相对增加全局搜索能力,有助于在更大空间内搜寻最优解;在后期r1加速递减,加快算法收敛,可以提升SCA的寻优精度和收敛速度。因此,r1(t)可以增加全局搜索能力,加快收敛速度,提升解的精度,证毕。 算法4 TSM-SCA机制 输入:节点数Ni(i=1,2,…,n)的负载能力Li,实时负载Ri,任务数Ti(i=1,2,…,m)。 输出:最优调度方案Pg=(pg1,pg2,…,pgN)。 //k表示種群数量,T表示最大迭代次数 initialize population individual k the maximum number of iterations T for t=1 to T do //Xi表示第i个个体 for each individual Xi do calculate fitness (Xi); //Pg表示当前最优个体 update the current best candidate solution Pg update ω(t)=ωmin+(ωmax-ωmin)[1-(t/T)2]; if (r4<0.5){ xt+1ij=ω(t)×xtij+r1×sin r2×|r3pgj-xtij|; } else { xt+1ij=ω(t)×xtij+r1×cos r2×|r3pgj-xtij|; } update r1(t)=a×[1-tan(π/4×t/T)]; end for end for //得到满足条件的最优个体 output the task scheduling scheme Pg=(pg1,pg2,…,pgN) //按照最优个体分配任务 assign tasks according to the task scheduling scheme Pg 2.4 PDF-SNRSCA算法的并行流程 PDF-SNRSCA算法的并行化流程具体实现步骤如下: a)从分布式文件系统HDFS中读取数据,调用FS-NRS策略对数据集进行特征降维,获取得到优质的特征集。 b)调用textFile()将优质的特征集转换为RDD形式,利用S-RSEE策略对优质的特征集进行训练,获取原始类向量,并调用saveAsTextFile()将其存入HDFS中。 c)集群中mapper节点从HDFS中读取原始类向量,将原始类向量的数据集转换为RDD数据,针对每个RDD的分区分别搭建子森林,训练子森林,调用ResultTask计算子森林的准确率,调用ShuffleMapTask得到每个子森林,训练得到类向量,将类向量写入到ShuffleWriter。 d)利用TSM-SCA机制,将每个RDD分区产生的类向量进行分组聚合操作,得到当前层的增强类向量。 e)从每个任务收集子森林的准确率并汇总结果,判断当前结果是否满足训练终止条件,若满足则停止计算,不满足则利用FFM-II机制得到下一层级的原始类向量且重复步骤c)~e)。 算法整体流程如图1所示。 2.5 算法时间复杂度分析 PDFS[7]、NID-PDF[8]和BLB-gcForest[9]等都是基于Spark框架设计的并行深度森林算法,并且采用不同的策略提高了算法性能。例如PDFS算法采用了基于索引的多粒度扫描算法,节省了存储空间,提高了训练效率;NID-PDF算法优化了RDD缓存替换策略,提高了并行效率;BLB-gcForest算法采用自助采样机制,减少了样本在级联森林层的传输,并且提出了自适应子森林划分算法,进一步提高了并行效率。因此选取它们与PDF-SNRSCA算法进行时间复杂度分析和实验对比。 PDF-SNRSCA算法的时间复杂度主要由特征预处理、多粒度扫描和级联并行化训练三部分组成,分别记为T1、T2、T3。 a)特征预处理阶段。该阶段的时间复杂度主要由筛选无关特征和过滤冗余特征两部分组成。假设当前数据样本数量为p,特征数量为c,则筛选无关特征阶段时间复杂度为O(c×p),过滤冗余特征阶段时间复杂度为O(c2);综上,特征预处理阶段的时间复杂度T1为 T1=O(c×p)+O(c2)(25) b)多粒度扫描阶段。该阶段的时间复杂度主要由随机扫描和等距提取两部分组成。假设样本数量为p,随机扫描规模为h,次数为b次,则随机扫描阶段的时间复杂度为O(b×h),等距提取阶段的时间复杂度为O(b);假设两个阶段迭代的次数为z次,则特征扫描阶段的时间复杂度T2为 T2=O(z×b×h)+O(z×b)+O(z)(26) c)级联并行化训练阶段。该阶段的时间复杂度主要由并行构建级联森林和负载均衡两部分组成。假设传入到级联森林的原始特征个数为v,样本数量为w,每一层森林的个数为s,每个森林包含r棵树,级联森林的层数为q,每个森林可划分为u子森林,则并行构建级联森林阶段的时间复杂度为O(w×s×r×q/u)+O(v×w+u);假设迭代次数为Iter,SCA算法初始化的个体数量为k,集群中节点个数为n,任务个数为m,则负载均衡阶段的时间复杂度为O(Iter×k×n+m)。综上,则级联森林并行化阶段的时间复杂度T3为 T3=O(w×s×r×q/u)+O(v×w+u)+O(Iter×k×n+m)(27) 综上所述,PDF-SNRSCA算法的时间复杂度为T=T1+T2+T3。在大数据环境下输入数据量十分庞大,且深度森林模型的时间复杂度主要由传入级联森林训练时的特征数量以及停止训练所需的层数决定,即算法的时间复杂度T中T3的v和q决定。对于特征v,由于算法PDFS、NID-PDF、BLB-gcForest都没有进行特征预处理,导致vPDFS>>vIPDF-NRS,vNID-DF>>vIPDF-NRS, vBLB-gcForest>>vIPDF-NRS;对于层数q,由于本文采用FFM-II策略加快了模型的收敛速度,使得所需的层数减少,从而使得qPDFS>>qIPDF-NRS,qNID-DF>>qIPDF-NRS,qBLB-gcForest>>qIPDF-NRS。因此,相比于其他三种算法,PDF-SNRSCA算法具有更低的时间复杂度。 3 实验结果与分析 3.1 實验环境 为了验证PDF-SNRSCA算法的性能,本文设计了相关实验。在硬件方面,本实验设置了8个计算节点,其中包含了1个master节点和7个slaver节点。各节点的配置均为Intel CoreTM i7-12700H CPU、16 GB DDR4 RAM、1TB SSD,且各节点处于同一局域网内,并通过1 Gbps以太网进行通信。在软件方面,每个计算节点上的软件配置均为Ubuntu 18.04.6、JDK 1.8.0、Apache Hadoop 2.7.7。各节点具体配置如表1所示。 3.2 实验数据 本文采用的实验数据为四个来自UCI公共数据库的数据集,分别为Nomao、TV news channel commercial detection(TNCCD)、FMA、MicroMass。Nomao是一个记录地点信息的数据集;TNCCD是一个记录电视新闻频道商业广告信息的数据集;FMA是一个记录各类歌曲信息的数据集;MicroMass是用于探索从质谱数据中识别微生物的数据集。各数据集的详细信息如表2所示。 3.3 评价指标 1)加速比 加速比是指同一个任务在串行系统和并行系统中执行所需时间的比率,用来衡量模型在并行系统下的性能提升,其定义为 其中:T1表示在串行系统下算法的执行时间;Tp表示在并行系统下算法的执行时间。 2)准确率 准确率是指分类模型正确分类的样本数与总样本数的比值,用来衡量模型的分类效果,其定义为 其中:TP、TN、FP、FN分別对应混淆矩阵中将正类样本预测为正类的样本数、将正类样本预测为负类的样本数、将负类样本预测为正类的样本数与将负类样本预测为正类的样本数。准确率的值越大,代表该分类模型的分类效果越好。 3.4 消融对比实验 为了验证PDF-SNRSCA算法中各策略的有效性,本文以算法的加速比和准确率为评价标准,使用深度森林作为基础模型,在MicroMass、Nomao、TNCCD和FMA数据集上进行消融实验。为了保证结果的可靠性,将算法在各个数据集上运行了5次,取5次的平均值作为最终结果,集群中节点的数目为8,森林中树的个数为200。实验结果如表3所示。 从表3可以看出,PDF-SNRSCA算法中不同的策略对算法加速比和准确率的影响不同,其中TSM-SCA和FFM-II策略对算法加速比的提升效果最为明显,FS-NRS策略次之,而S-RSEE策略对其无明显影响。当处理样本少特征多的数据集MicroMass时,使用TSM-SCA、FFM-II和FS-NRS策略分别比不使用这些策略时,算法加速比提升了9.87%,5.07%,1.60%,而使用S-RSEE策略比不使用这些策略时,算法加速比基本无明显变化;当处理样本多特征多的数据集FMA时,使用TSM-SCA、FFM-II和FS-NRS策略分别比不使用这些策略时,算法加速比提升了16.11%、10.15%、3.82%,而使用S-RSEE策略比不使用这些策略时,算法加速比同样基本无明显变化。产生这样结果的原因是:a)FFM-II机制可以平衡增强向量和原始向量的维度,加快了模型收敛速度,提高了算法的加速比;b)TSM-SCA机制能够寻找最优的调度方案,实现负载均衡,进一步提高了并行化效率;c)FS-NRS策略过滤了原始数据集中大量的冗余和不相关特征,减少了冗余和不相关特征的计算,因此对加速比的提升有一定的帮助;d)S-RSEE策略只是提高了两端特征的利用率,并没有过滤特征、平衡向量的维度和重新分配集群中的任务,所以其对提升模型的并行处理能力影响不大。 对算法准确率影响较大的是FS-NRS和S-RSEE策略,FFM-II策略次之,而TSM-SCA策略对其无明显影响。当处理样本少特征多的数据集MicroMass时,使用FS-NRS、S-RSEE、FFM-II分别比不使用这些策略时,算法准确率提升了1.11%、0.63%、0.31%,而使用TSM-SCA策略比不使用这些策略时,算法准确率基本无明显变化;当处理样本多特征多的数据集FMA时,使用FS-NRS、S-RSEE、FFM-II分别比不使用这些策略时,算法准确率提升了1.56%、1.04%、0.48%,而使用TSM-SCA策略比不使用这些策略时,算法准确率同样基本无明显变化。产生这些结果的原因是:a)FS-NRS策略通过过滤冗余及不相关特征,极大地提升了算法精度;b)S-RSEE策略使得特征同概率被选取,提高了两端特征利用率,进而提高了算法的准确率;c)FFM-II策略通过重要性指数的特征筛选机制,筛选出非关键性特征,对提升算法准确率有一定的帮助;d)TSM-SCA策略将集群中的任务进行重新分配,但对算法结构没有进行优化,因此对算法的准确率没有影响。 由此可得,FS-NRS、S-RSEE、FFM-II和TSM-SCA策略在大数据环境下具有良好的可行性与有效性。 3.5 算法性能比较分析 1)算法准确率比较分析 为了验证PDF-SNRSCA的分类效果,本节以准确率作为评价指标,在上述四个数据集上对PDF-SNRSCA、PDFS、NID-PDF和BLB-gcForest算法分別进行了5次测试,并取5次准确率的均值作为最终的实验结果,如图2所示。 从图2可以看出,随着森林中决策树的增加,各个算法的准确率也在不断提升,但本算法在四个数据集上的准确率,均高于其他三个算法。其中,当森林中决策树数量为200时,在处理MicroMass数据集时,PDF-SNRSCA算法的准确率比其他三个算法分别高出了0.38%、0.83%、0.95%;在处理Nomao数据集时,PDF-SNRSCA算法的准确率、其他三个算法分别高出了0.83%、1.22%、1.55%;在处理TNCCD数据集时,PDF-SNRSCA算法的准确率比其他三个算法分别高出了0.81%、1.45%、1.67%;在处理FMA数据集时,PDF-SNRSCA算法的准确率比其他三个算法分别高出了1%、1.5%、1.93%。产生上述结果的原因如下:a)PDF-SNRSCA算法设计了FS-NRS策略,对特征进行筛选,消除了原始特征集合中大量的冗余及无关特征,提高了准确率;b)PDF-SNRSCA算法设计了S-RSEE策略,使得特征同概率被选取,解决了两端特征利用率过低的问题,提高了整个模型的准确率;c)FFM-II策略通过重要性指数的特征筛选机制,筛选出非关键性特征,也对提升算法准确率有一定的帮助。实验结果由此表明,PDF-SNRSCA算法在大数据环境下具有良好的分类性能。 2)算法运行时间实验分析 为了验证PDF-SNRSCA算法的时间复杂度,本文在上述四个数据集上对PDF-SNRSCA、PDFS、NID-PDF和BLB-gcForest算法分别进行了5次测试,并取5次运行时间的均值作为最终的实验结果,如图3所示。 从图3中可以看出,在处理四个数据集时,PDF-SNRSCA算法所需要的运行时间都是最低的,并且在处理特征数量多的数据集时,PDF-SNRSCA算法相较于其他三种算法具有更好的优势。其中,在处理特征数量较多的MicroMass时,PDF-SNRSCA算法的运行时间比其他三种算法,分别缩短了13.46%、11.12%、22.23%;在处理特征数量较少TNCCD时,PDF-SNRSCA算法的运行时间比其他三种算法分别缩短了3.23%、4.43%、9.78%。出现上述现象的主要原因为:a)PDF-SNRSCA算法设计了FS-NRS策略,对特征进行筛选,消除了原始特征集合中大量的冗余及无关特征,从而加快了训练速度;b)PDF-SNRSCA算法提出了FFM-II机制,促进了增强类向量和原始类向量的平衡,加快了模型的收敛速度。由此表明,PDF-SNRSCA算法在处理大数据问题时具有出色的性能。 3)算法加速比实验分析 为了评估PDF-SNRSCA算法在大数据环境下的并行性能,本文在上述四个数据集上对PDF-SNRSCA、PDFS、NID-PDF和BLB-gcForest算法分别进行了5次测试,并用5次运行时间的均值来计算各算法在不同计算节点个数下的加速比。实验结果如图4所示。 从图4可以看出,在处理MicroMass、Nomao、TNCCD和FMA四个数据集时,各算法在四个数据集上的加速比随着节点数量的增加而逐渐上升,并且随着数据规模的逐步扩大,PDF-SNRSCA算法在各数据集上的加速比远超其他三种算法。例如,在处理数据规模较小的数据集MicroMass时,当节点为8时(图4(a)),PDF-SNRSCA算法的加速比相较于其他三种算法分别增加了0.111、0.201、0.32;在处理数据规模较大的数据集TNCCD和FMA时,当节点为8时(图4(c)(d)),PDF-SNRSCA算法在TNCCD数据集上的加速比,相较于其他三个算法分别高了0.479、0.928、1.054,PDF-SNRSCA算法在FMA数据集上的加速比,相较于其他三个算法分别高了0.345、0.803、0.678。出现上述现象的原因为:a)当数据规模较小时,节点通信时间占总运行时间过长,通过并行计算提升的时间有限,不足以弥补通信所消耗的时间;b)当数据规模较大时,TSM-SCA机制将任务重新进行分配,实现了节点之间的负载平衡,提升了模型的并行化效率,使得算法在处理数据时具有更高的加速比。以上实验表明,PDF-SNRSCA算法在处理大数据问题时,相比其他算法具有更高的加速比。 4 结束语 为了克服在大数据环境下深度森林算法的不足,本文提出了PDF-SNRSCA算法。首先,该算法提出了FS-NRS策略,对特征进行筛选,有效减少了冗余及无关特征的数量;其次,设计S-RSEE策略,替代传统的多粒度扫描,解决了两端特征利用率过低的问题;然后,提出了FFM-II特征筛选机制,以此促进增强类向量与原始类向量之间的平衡,解决了模型收敛速度慢的问题;最后,提出了TSM-SCA任务调度机制,将节点的任务重新进行分配,解决了级联森林并行效率低的问题。为了验证本文算法性能,将其与PDFS、NID-PDF和BLB-gcForest等算法在Nomao、 TNCCD、FMA、MicroMass上进行比较验证,最终实验结果表明,PDF-SNRSCA算法可以有效处理大规模的数据集合,并且具有很好的分类效果。虽然PDF-SNRSCA算法在大数据环境下表现出良好的训练效果,但其仍有一些不足:a)特征预处理阶段计算时间过长;b)级联森林并行化阶段中,级联森林的并行粒度较低。所以未来的工作重点在于如何更加有效地进行特征筛选,以及如何进一步对深度森林进行划分,使得并行粒度和节点通信开销达到一个新的平衡。 参考文献: [1]Zhou Zhihua, Feng Ji. Deep forest[J].National Science Review,2019,6(1):74-86. [2]Mou Luntian, Mao Shasha, Xie Haitao, et al. Structured behaviour prediction of on-road vehicles via deep forest[J].Electronics Letters,2019,55(8):452-455. [3]Yaakoub B, Mohamed F, Imed R F. Remote sensing scene classification using convolutional features and deep forest classifier[J].IEEE Geoscience and Remote Sensing Letters,2019,16(12):1944-1948. [4]Hu Guangzheng, Li Huifang, Xia Yuanqing, et al. A deep Boltzmann machine and multi-grained scanning forest ensemble collaborative method and its application to industrial fault diagnosis[J].Computers in Industry,2018,100:287-296. [5]陳吕鹏,殷林飞,余涛,等.基于深度森林算法的电力系统短期负荷预测[J].电力建设,2018,39(11):42-50.(Chen Lyupeng, Yin Linfei, Yu Tao, et al. Short-term power load forecasting based on deep forest algorithm[J].Electric Power Construction,2018,39(11):42-50.) [6]毛伊敏,甘德瑾,廖列法,等.基于Spark框架和ASPSO的并行划分聚类算法[J].通信学报,2022,43(3):148-163.(Mao Yimin, Gan Dejin, Liao Liefa, et al. Parallel division clustering algorithm based on Spark framework and ASPSO[J].Journal on Communications,2022,43(3):148-163.) [7]Li Xuebing, Sun Ying, Zhuang Fuzhen, et al. Potential off-grid user prediction system based on Spark[J].ZTE Communications,2019,17(2):26-37. [8]Liu Zhenpeng, Su Nan, Qin Yiwen, et al. A deep random forest model on Spark for network intrusion detection[J].Mobile Information Systems.(2020-01-01).https://doi.org/10.1155/2020/6633252. [9]Chen Zexi, Wang Ting, Cai Haibin, et al. BLB-gcForest:a high-performance distributed deep forest with adaptive sub-forest splitting[J].IEEE Trans on Parallel and Distributed Systems,2022,33(11):3141-3152. [10]Yin Tengyu, Chen Hongmei, Yuan Zhong, et al. Noise-resistant multilabel fuzzy neighborhood rough sets for feature subset selection[J].Information Sciences,2022,621:200-226. [11]Pang Jing, Yao Bingxue, Li Lingqiang. Generalized neighborhood systems-based pessimistic rough sets and their applications in incomplete information systems[J].Journal of Intelligent & Fuzzy Systems,2022,42(3):2713-2725. [12]Sun Lin, Yin Tengyu, Ding Weiping, et al. Multilabel feature selection using ML-ReliefF and neighborhood mutual information for multi-label neighborhood decision systems[J].Information Sciences,2020,537:401-424. [13]Zhang Di, Zhu Ping. Variable radius neighborhood rough sets and attribute reduction[J].International Journal of Approximate Reasoning,2022,150:98-121. [14]Xu Sixiang, Damien M, Alain T. Sparse coding and normalization for deep Fisher score representation[J].Computer Vision and Image Understanding,2022,220:103436-103439. [15]Li Changlun, Liang Ke, Chen Yuan, et al. An exploitation-boosted sine cosine algorithm for global optimization[J].Engineering Applications of Artificial Intelligence,2023,117:105620-105630.
