3 刚度计算公式可靠性验证
3.1 有限元模型
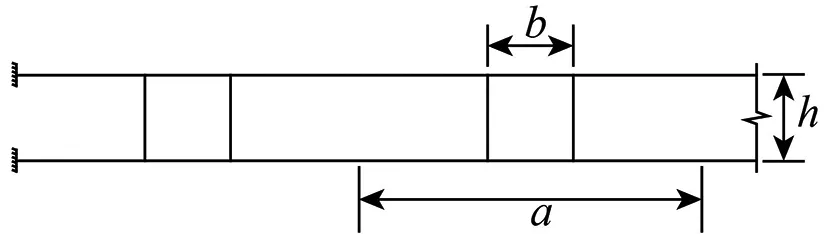
有限元模型参数如图7所示,双竖杆空腹桁架跨度L、节间距a、竖杆间距b、桁架高度h、上下弦宽度w1、上下弦高度h1、上下弦翼缘厚度t1、上下弦腹板厚度t2、竖杆截面宽度w2、竖杆高度h2、竖杆翼缘和腹板厚度t3。

(a)双竖杆空腹桁架
有限元模型采用ANSYS有限元模拟中常用的网格划分方法实现。Shen等[17]对未考虑钢筋混凝土板的空腹梁进行实验研究,把壳单元和梁单元模拟的空腹梁结果与实验结果对比分析,结果表明壳单元与梁单元模拟空腹梁精度较高,误差在5%以内。
工程实际一般采用梁单元进行结构设计,因此采用SHELL181单元和BEAM188单元模拟,并与等代刚度法计算结果对比分析。支座采用固定支承,钢材弹性模量为2.06×105MPa,泊松比为0.3,剪切模量为7.9×104MPa。
3.2 参数化分析
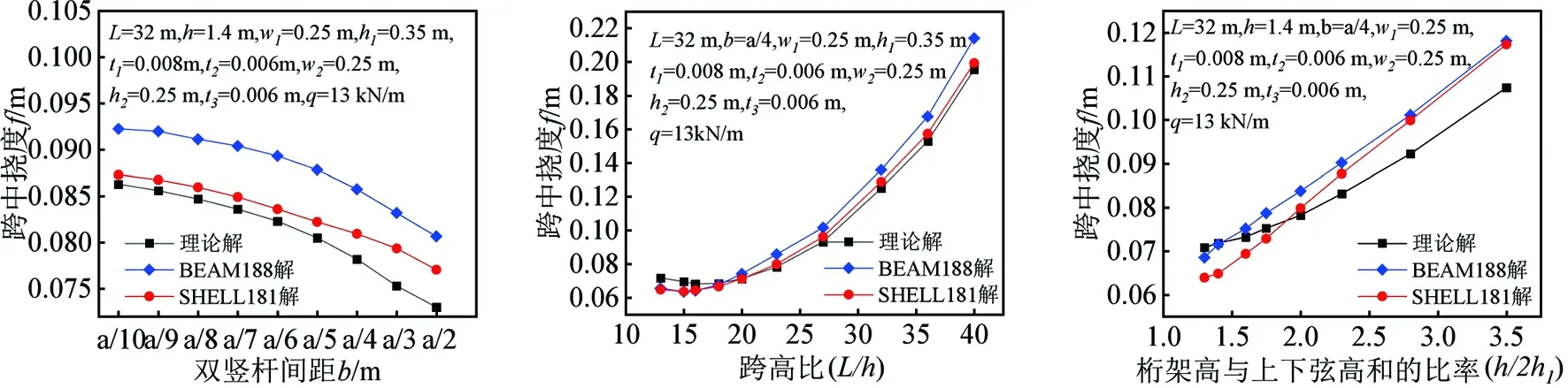
取模型初始参数:q=13 kN/m双竖杆空腹桁架跨度L=32 m、节间距a=3.2 m、竖杆间距b=a/4、桁架高度h=1.4 m、上下弦宽度w1=0.25 m、上下弦高度h1=0.35 m、上下弦翼缘厚度t1=0.008 m、上下弦腹板厚度t2=0.006 m、竖杆截面宽度w2=0.25 m、竖杆高度h2=0.25 m、竖杆翼缘和腹板厚度t3=0.006 m,建立有限元模型对比分析如图8所示。由图8可得以下几点结论:
(a)改变竖杆间距 (b)改变跨高比 (c) 改变桁架高与上、下弦高和的比率
由图8(a)所示,随着竖杆间距不断增大,跨中挠度逐渐减小,说明双竖杆空腹桁架刚度随着竖杆间距增大而增大,竖杆间距为a/2时刚度最大。
由图8(b)所示,随着跨高比的增大,跨中挠度先减小后增大;说明桁架高度过大时,腹杆长细比较大,由剪力引起的局部弯曲变形较大,从而导致跨中挠度较大;跨度不变,桁架高度减小时,桁架整体抗弯刚度减小,跨中挠度大幅增加。
由图8(c)所示随双竖杆空腹桁架高度与上下弦高度和的比率增大,桁架跨中挠度增大;双竖杆空腹桁架高度与上下弦高度和的比率较小时,上下弦截面高占桁架高度较大比重,桁架抗弯刚度与等效剪切刚度均较大,跨中挠度较小;反之,桁架抗弯刚度与等效剪切刚度均较小,跨中挠度较大。
由图8(d)、(e)所示,桁架跨中挠度随上下弦截面宽度和上下弦翼缘厚度的增加而减小;上下弦截面宽度和翼缘厚度的增加使桁架抗弯刚度大幅增加,桁架挠度自然减小。
由图8(f)所示,桁架挠度随荷载不断增加而增加,荷载与挠度成正比例关系。
图8中BEAM188、SHELL181单元模拟的双竖杆空腹桁架挠度值与理论值误差均在10%以内,理论值与SHELL181单元模拟值更接近,说明公式(5)与公式(11)用于计算双竖杆空腹桁架刚度有很高的可靠性。
4 性能对比分析
以b=a/4的固定支座双竖杆空腹桁架为例,与传统单竖杆空腹桁架进行对比研究,模型结构相关参数如图9所示。跨度L、节间距a、竖杆间距b、桁架高度h、上下弦宽度w1、上下弦高度h1、上下弦翼缘厚度t1、上下弦腹板厚度t2、竖杆截面宽度w2、竖杆高度h2、竖杆翼缘和腹板厚度t3。

(a)空腹桁架
4.1 用钢量控制相同的条件下刚度及内力对比分析
4.1.1 刚度对比
刚度等代后,用式计算双竖杆空腹桁架的跨中挠度,用式(2)计算等效惯性矩,用式(12)计算等效剪切刚度,并与传统空腹桁架对比分析。为了确保刚度是影响挠度的唯一因素,使用钢梁基本相同。传统空腹桁架等效惯性矩与双竖杆空腹桁架相同,等效剪切刚度公式为[7]:
(14)
式中弯矩和剪力引起的变形通过图乘法求出。两种结构采用式计算的跨中挠度、等效惯性矩和等效剪切刚度见表1。

表1 模型参数及计算结果
由表1可以看出,设计条件及用钢量基本相同的条件下,双竖杆空腹桁架挠度更小。双竖杆空腹桁架两种不同竖杆间距的等效剪切刚度分别是传统空腹桁架的1.3、1.4倍。两种不同的竖杆间距,最大挠度为传统空腹桁架的87%、84.4%。
4.1.2 内力对比
为了研究双竖杆空腹桁架的内力分布规律及优劣,对传统空腹桁架结构和双竖杆空腹桁架结构进行内力分析和对比,模型参数如图9所示,具体参数与表1相同。两端固定的空腹桁架内力最大处为支座附近,传统空腹桁架与双竖杆空腹桁架支座附近的内力如图10所示。
由图10可以看到,双竖杆空腹桁架的上下弦最大弯矩和最大剪力较单竖杆空腹桁架分别减小了35.3%和7.2%,双竖杆空腹桁架的腹杆最大弯矩和最大剪力较单竖杆空腹桁架分别减小了39.5%和39.1%。空腹桁架由单竖杆变为双竖杆之后,内力峰增多,峰值并趋于缓和。上下弦构件截面由最大内力控制,双竖杆空腹桁架上下弦内力沿构件分布更均匀,峰值小,理论上截面也会随之减小。

(a) 单竖杆空腹桁架弯矩图 (b) 单竖杆空腹桁架剪力图 (c) 单竖杆空腹桁架轴力图 (d) 双竖杆空腹桁架弯矩图 (e) 双竖杆空腹桁架剪力图 (f) 双竖杆空腹桁架轴力图图10 内力比较
4.2 挠度和最大应力满足规范的条件下性能对比分析
采用基于响应面法的结构优化设计方法[18]对传统空腹桁架结构与双竖杆空腹桁架结构进行优化设计,并在两种结构最优状态下对比分析其经济性及实用性。
4.2.1 设计流程
以结构质量为目标函数,最大组合应力、最大挠度和构件宽厚比为约束条件。
(15)
为防因构件局部屈服致整体结构破坏,建立应力约束条件σ≤[σ],约束值为Q345钢的屈服强度。为了满足整体结构刚度要求和舒适度要求建立最大挠度约束f≤[f],根据《钢结构设计标准》规定的楼盖挠跨比1/400[19],32 m跨度允许挠度为0.08 m。为了保证局部稳定性,根据《抗震设计规范》按一级抗震标准约束宽厚比[20],β1为上下弦翼缘宽厚比,β2为上下弦腹板宽厚比,β3为腹杆宽厚比。根据H型钢规格表获取各设计变量的取值范围,在范围内取可制造离散值。设计变量及约束条件见表2。

表2 设计变量和约束条件
设计变量、目标函数和约束条件确定后,通过Box-behken实验设计获取数值实验样本点;构建Kriging响应面,获取近似响应点;采用MOGA遗传算法,对空腹桁架进行优化设计,优化流程如图11所示。
在对脑梗塞患者进行护理期间,针对患者心理需要给予充分照顾,对于系列异常可以做到及时处理以及疏导,对于患者的积极思考加以充分引导,确保对于现实可以做到勇敢面对,将自身思维模式加以端正[2]。

图11 优化流程
4.2.2 结果分析
根据以上优化流程得到传统空腹桁架与双竖杆空腹桁架的最优解,两种结构的构件截面参数、结构最大挠度、最大组合应力、结构质量见表3。由表3可得出以下结论:
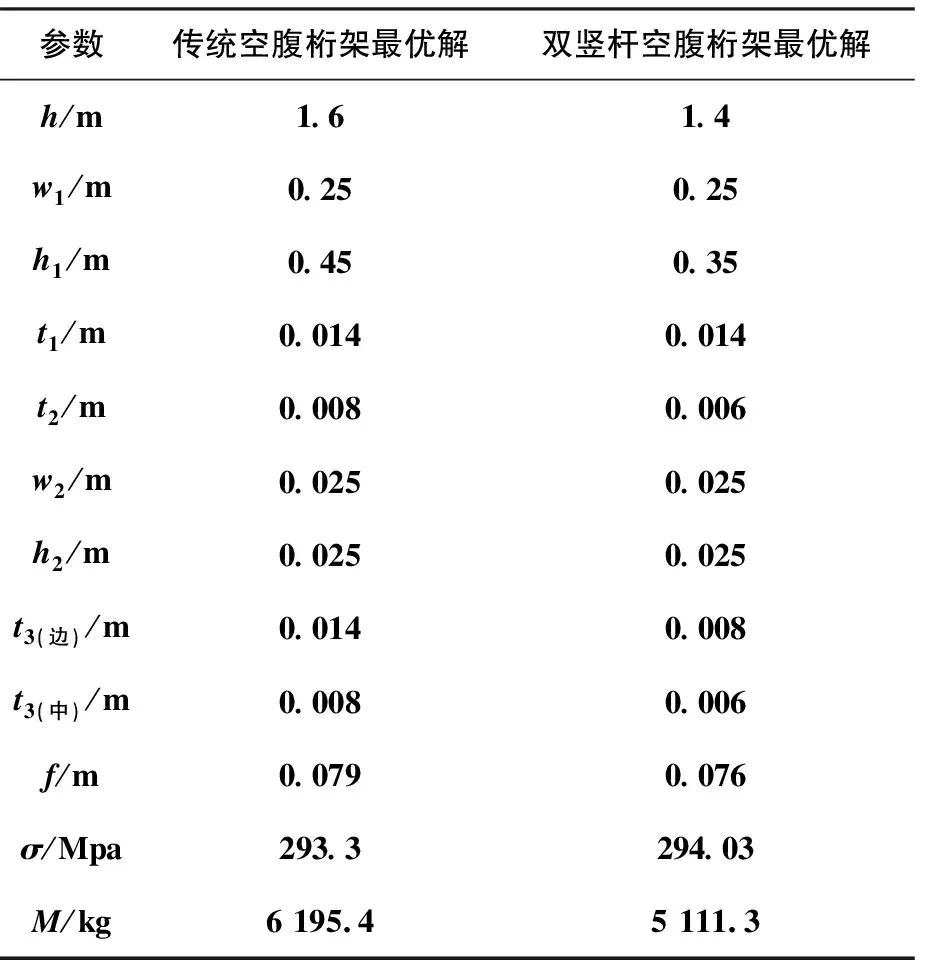
表3 优化设计结果
1)在相同条件下,双竖杆空腹桁架结构高度减小了0.2 m,在工程中应用双竖杆空腹桁架结构每层可节省层高0.2 m。
2)双竖杆空腹桁架结构上下弦高度减小了0.1 m。腹部空间净高为桁架高度减去上下弦高度,传统空腹桁架与双竖杆空腹桁架腹部空间净高均为0.7 m。说明双竖杆空腹桁架结构高度小,腹部空间大,腹部空间利用率较高。
3)挠跨比、最大组合应力满足规范要求的前提下传统空腹桁架用钢量6.2 t,双竖杆空腹桁架用钢量5.1 t,相比传统空腹桁架结构用钢量减少了1.1 t,节省用钢量17.5%。说明与传统空腹桁架结构相比,实际建筑工程采用双竖杆空腹桁架结构造价更低。
5 结论
本文通过等效剪切刚度分析与有限元相结合的方法分析了双竖杆空腹桁的整体刚度和技术经济性能,得到以下结论:
1)推导了双竖杆空腹桁架等效惯性矩和等效剪切刚度公式,并经过参数化分析验证出公式的可靠性,可用于简化求解双竖杆空腹桁架结构。
2)经过等效剪切刚度分析,得到了双竖杆合理取值范围。相同用钢量的条件下,通过刚度对比分析得出,双竖杆空腹桁架整体刚度是传统空腹桁架整体刚度的1~1.4倍。
3)在用钢量相同的条件下与传统空腹桁架静力对比分析得出,双竖杆空腹桁架的上下弦弯矩和剪力分别减小了35.3%和 7.2%,腹杆的弯矩和剪力分别减小了39.5%和39.1%。
5)双竖空腹桁架结构刚度大、桁架高度低,该类结构的建筑空间利用率高、结构造价低,具有很好的工程应用前景。
[1]童骏. 某大跨转换桁架高层钢结构设计[J]. 建筑钢结构进展, 2020, 22(4): 103-109.
[2] 张龑华, 甄伟, 盛平, 等. 某带高位长悬挑桁架的超限结构设计[J]. 建筑结构, 2020, 50(20): 23-30.
[3] 简斌, 钟庆, 甘渊, 等. 预应力混凝土空腹桁架转换结构低周反复荷载试验研究[J]. 土木工程学报, 2013, 46(12): 18-24.
[4] 丁井臻, 邢万里, 王赞, 等. 长春复华未来世界I期连体及大悬挑结构设计[J]. 建筑结构, 2019, 49(S2): 69-75.
[5] 陈方, 陈寅, 廖耘. 珠海横琴国际交易广场复杂连体结构创新设计[J]. 建筑结构, 2020, 50(4): 118-123.
[6]董石麟,马克俭,等.组合网架结构与空腹网架结构[M]. 杭州:浙江大学出版社,1992.
[7] 肖建春, 马克俭, 董石麟. 空腹网架及空腹夹层板的折算剪切刚度[J]. 建筑结构, 2000,30(4): 39-41,54.
[8] 张华刚, 马克俭. 空腹夹层板刚度分析的简化算法及其静力性能分析[J]. 贵州工业大学学报(自然科学版), 2003(5): 66-71.
[9] 李玉莹, 梁书亭, 孙修礼, 等. 空腹桁架结构受力机理研究分析[J]. 工业建筑, 2006(S1): 427-430,412.
[10]刘卓群, 肖建春, 赵勇, 等. 剪力键式钢空腹梁空腹部分内力计算方法研究[J]. 钢结构, 2017, 32(10): 19-24.
[11] 姜岚, 马克俭, 张华刚, 等. 剪力键式钢空腹梁静力计算方法[J]. 西安建筑科技大学学报(自然科学版), 2018, 50(3): 354-360.
[12] 肖建春, 谈若明, 马克俭. 双竖腹杆空腹桁架与方钢管连接π型节点的极限承载力[J]. 工业建筑, 2009(S1): 499-502,528.
[13]姚谏,董石麟.建筑结构静力计算手册[M].北京:中国建筑工业出版社,2021.
[14] 陈顺云, 肖建春, 沈睿麟, 等. 基于响应面法的钢空腹桁架结构优化设计[J]. 建筑科学与工程学报, 2022(10): 1-9.
[15] 马克俭,张华刚,郑涛. 新型建筑空间网格结构理论与实践[M].北京: 人民交通出版社,2006.
[16] 孙涛, 马克俭, 刘宪庆, 等. 钢空腹夹层板结构等效剪切刚度分析[J]. 空间结构, 2017, 23(2): 54-59,69.
[17] SHEN R, XIAO J, MA K, et al. Theoretical and experimental study on steel open-web sandwich floor with flanged cruciform section shear key[J]. Latin American Journal of Solids and Structures,2020, 17(3): e260.
[18] 柴山,尚晓江,刚宪约,等.工程结构优化设计方法与应用 [M].北京:中国铁道出版社,2015.
[19] 中华人民共和国住房和城乡建设部.钢结构设计标准:GB50017—2017 [S].北京:中国建筑工业出版社,2017.
[20] 中华人民共和国住房和城乡建设部.建筑抗震设计规范: GB50011—2010 [S].北京:中国建筑工业出版社,2010.