含孔洞多裂隙复合岩层裂纹扩展和分形特性模拟研究

汪学清 ，赵云猛 ，冯 莹 ，汪壮壮 ，李永超 ，陈 博 ，董 泽 ，吴帅军

（1.中国矿业大学（北京）力学与建筑工程学院，北京 100083；2.深海矿产资源开发利用技术国家重点实验室，湖南 长沙 410012）

在隧道、地铁、采矿等工程的洞室开挖过程中，稳定性问题一直备受关注。自然界中由2 种或2 种以上不同岩层所构成，且每层岩石的力学性质和地质状态均有较大差别的被称为复合岩层。在复合岩层中洞室开挖成为实际工程中常见的工程问题之一。在受外部荷载的作用及应力重分布下，复合地层中裂纹的起裂、扩展和贯通过程会影响洞室围岩的受力，进而导致岩体的垮塌。因此，研究含孔洞复合岩层的破坏过程对开挖工程的安全性和稳定性有着重要的意义。

考虑到原位测试的复杂性和其他不确定因素，大多数试验是在现场取样或根据相似理论[1-2]制作类岩石材料并在实验室内完成，所以单轴压缩试验[3]、三轴压缩试验[4-5]、巴西劈裂试验[6-7]等是研究复合岩层的常用方法。殷鹏飞[8]通过单轴压缩试验研究了不同的层理倾角的复合类岩层试件的破坏模式和力学特性，并结合声发射分析试样的破坏过程，详细解释了不同层理倾角的复合岩层裂纹起裂、扩展过程；邵光钦[9]利用类岩石研究了含预制裂隙的复合岩层在单轴压缩下的破坏模式，发现层理倾角较大时会发生脆性断裂，但是预制裂隙与界面贯通会影响试验结果的准确性；程建龙等[10]利用三轴试验研究了复合岩层的强度特性和破坏模式，并发现部分裂纹数量与裂纹方向符合正态分布统计规律；王辉等[11]利用巴西劈裂试验研究了页岩在不同层理倾角下的破坏模式和裂纹长度，证明了试件强度与裂纹长度有一定的关系，发现声发射得到声发射计数出现单峰陡增时，试件为拉伸破坏，出现多段增长时，试件为剪切和拉伸破坏；当岩层内含有洞室时，TANG 等[12]改变孔洞的大小、位置和分布，发现影响孔洞大小会影响裂纹起裂应力，分布会影响裂纹扩展速度和方向；张科等[13]在含孔岩石内加入预制裂隙，改变裂隙倾角将岩石破坏分为穿切裂隙剪切破坏和沿裂隙剪切破坏模式。

很多学者对含孔和裂隙的单一岩体扩展进行分析，但对复合岩层研究较少。因此，提出了一种新的含孔洞和裂隙复合岩层的模型，利用数值模拟对复合岩层的力学特性和分形特征进行研究。

1 RFPA2D 数值模型及参数

采用RFPA2D建立了含孔和裂隙的复合岩层模型，假定服从摩尔-库伦准则，包含2 种软硬岩A、B，软硬岩A、B 的细观力学参数见表1[14]。模型尺寸为130 mm×160 mm，圆孔直径32 mm，划分了260×320=83 200 个等面积细观单元。预制裂隙的细观力学参数为：弹性模量1 000 MPa，抗压强度3 MPa。

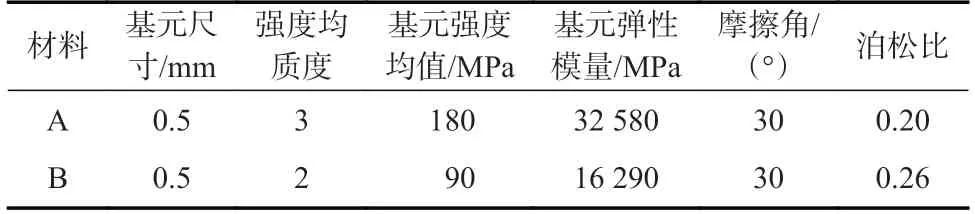
表1 软硬岩A、B 的细观力学参数Table 1 Meso-mechanical parameters of hard and soft rocks A and B

本文数值模拟与文献[14]中的复合岩层破坏模式对比如图1，试验的力-加载步数曲线如图2。

图1 本文数值模拟与文献[14]中的复合岩层破坏模式对比Fig.1 Comparison between numerical simulation in this paper and literature [13] failure modes of composite strata

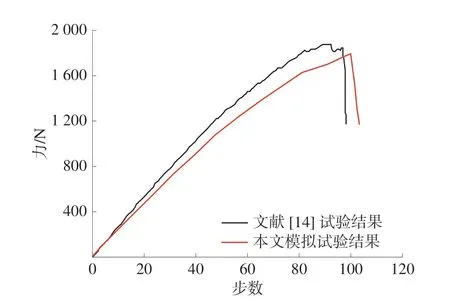
图2 试验的力-加载步数曲线Fig.2 Force-loading step curves of the test

由图1（a），加载初期裂纹从孔洞最高和最低点开始，然后沿着最大主应力方向（竖直方向）发展，随着加载步数的增加，软岩层内出现远场裂纹并主要在副对角线上扩展，远场裂纹逐渐穿过硬岩层产生拉裂纹导致模型试件发生破坏；图1（a）的试验结果与图1（b）的试验结果相比，破坏模式有较小差别。

由图2，2 次试验的力-加载步数曲线变化趋势一致，峰值力相差2.3%，这是由于基元弹性模量均质度不同，文献[14]中并未提及基元弹性模量均质度取值（表1），本文通过试错法得到材料A、B 基元弹性模量均质度取值均为3。

德国现行的垃圾处理技术政策，已经从单一的无害化向“减量化、资源化、无害化”转变：①进一步完善分类收集系统，确保将生活垃圾在源头有效分类，从而保证垃圾回收利用的效果；②开发先进的机械生物处理技术，对混合生活垃圾进行合理分选，以提高垃圾资源利用的效果；③对焚烧技术进一步优化，以适应各种垃圾的性质、降低污染物排放、提高能源利用效率的目标；④充分发挥创新精神，将科技运用到各种细节中，如垃圾收运车采用混合动力或绿色动力等。同时，德国部分垃圾处理设施是以园区的形式建设的，集垃圾处理、环保公园、动物饲养、休闲娱乐等设施于一体，园区边界与居民区之间没有防护距离，取得公众的高度信任。

为简化分析，数值模型未考虑开挖过程、岩石支护和加固的影响，数值模型如图3。

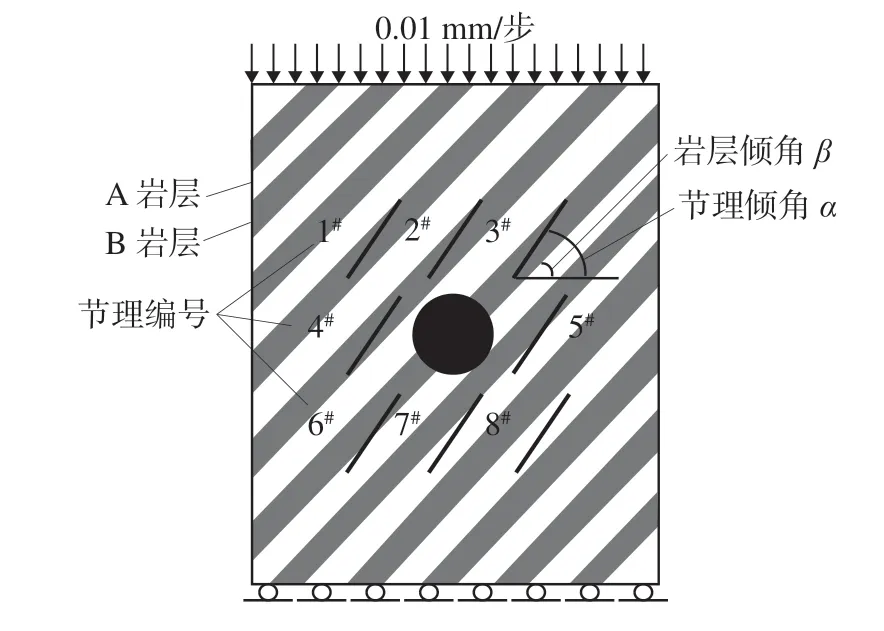
图3 数值模型Fig.3 Numerical model

为了模拟完整的应力-应变曲线，以0.01 mm/步的位移速度控制加载大小。在位移控制下竖向加载直至模型失稳，每一步基元都会在过度的张力下屈服于摩尔-库仑准则而发生损坏，然后在每个基元破裂后，RFPA2D软件会瞬间调整整个模型试件的应力和变形分布，使其重新达到平衡状态。由于应力的重新分布，模型试件承受的载荷增加可能会引起进一步的断裂。重复该过程，直到基元中不再发生失稳，然后施加更多的外部荷载，在加载过程中能量被存储在基元中，这种能量在基元失效时以声发射的形式释放出来。

2 数值模拟结果

RFPA2D模拟了复合岩层完整的破坏过程，从裂纹的开裂到扩展再到贯通，为了便于描述不同裂纹的发育过程，将裂纹分为拉伸裂纹（T）、剪切裂纹（S）、远场裂纹（R）。在RFPA2D声发射中定义拉伸裂纹为红色，剪切裂纹为蓝色，远场裂纹的定义是根据裂纹在除预制裂隙和圆孔的位置开裂。

2.1 裂隙倾角（α）对含孔复合岩层的影响

数值试验过程中，复合岩层倾角（β）不变，裂隙倾角0°、30°、45°、60°、90°变化，不同裂隙倾角下裂纹扩展过程和声发射图如图4，图4 中裂隙编号与图3 中同位置裂隙编号相同。

图4 不同裂隙倾角下裂纹扩展过程和声发射图Fig.4 Crack propagation process and AE diagrams at different inclination angles

加载初期，初始裂纹均会从圆孔上下两应力集中区开裂，随着不断地加载，裂纹沿着最大主应力方向（竖直方向）扩展到圆孔上下两预制裂隙处，然后预制裂隙两端开始萌生剪切裂纹，由于裂隙倾角不同导致裂纹开裂的方式和时间也不同。根据开裂后裂纹的整体分布，破坏模式被分为2 类：Y 型破坏模式和X 型破坏模式。

1）当α=0°、60°、90°时，裂纹主要沿着对角线（α=0°、60°为副对角线；α=90°为主对角线）一侧最大主应力方向扩展。初始裂纹到达上下两预制裂隙后扩展速度变慢，对角线处预制裂隙两端开始产生拉伸翼形裂纹，并沿模型试件的对角线上下扩展，1 个角处（图4（a）3#、图4（b）6#、图4（c）8#）裂纹扩展速度较快，其余3 个角处扩展较慢。继续加载，裂纹与圆孔贯通，裂隙另一端（图4（a）3#右端、图4（b）6#左端、图4（c）8#下端）剪切裂纹扩展速度加快，最后到达模型试件边缘也随之发生失稳破坏，其整体破坏为Y 型破坏模式。

2）当α=30°、45°时，随着不断地加载，副对角线预制裂隙两端发生应力集中的现象，拉伸翼形裂纹从裂隙（图4（d）3#和6#、图4（e）3#和6#）两端开始扩展，圆孔一侧的裂纹（#3#左端和#6#右端）沿着副对角线方向达圆孔边缘。随后另一端（3#右端和6#左端）产生的剪切裂纹沿着最大主应力方向扩展与边界连通，孔洞发生垮塌，随后模型试件整体贯通形成沿裂隙面滑移的宏观剪切破坏，其整体破坏为X 型破坏模式。

2.2 裂纹扩展的力学和声学解释

绘制了裂隙倾角0°、30°、45°、60°、90°的应力-应变曲线和声发射数-步数曲线，不同裂隙倾角的应力-应变曲线、声发射数-步数和分形维数-步数曲线如图5。

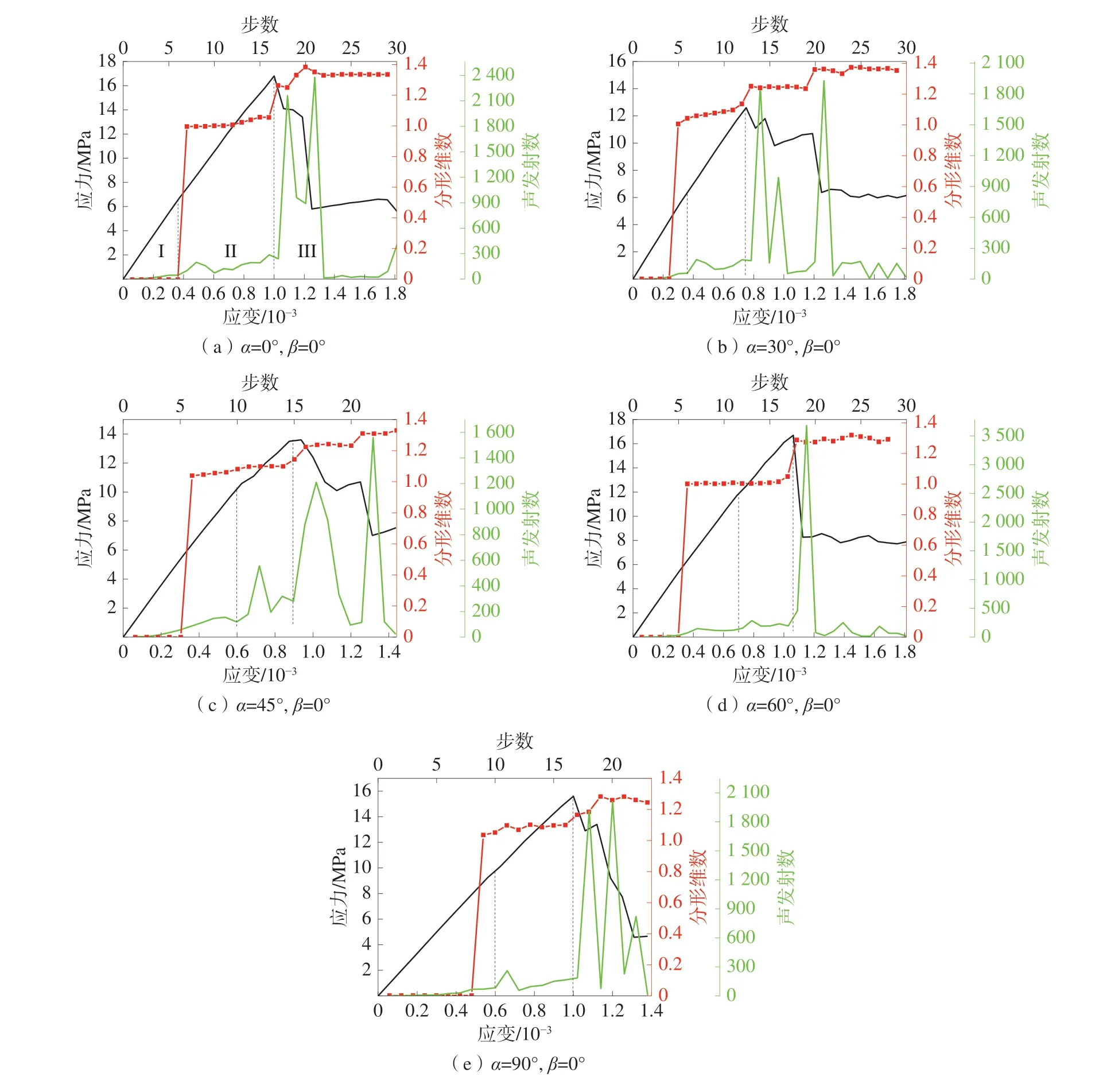
图5 不同裂隙倾角的应力-应变曲线、声发射数-步数和分形维数-步数曲线Fig.5 Stress-strain curves,AE numbers-step curves and fractal dimensions-step curves of different fracture inclination angles

不同裂隙倾角的应力-应变曲线大致可分为3个阶段：弹性阶段（I）、弹塑性阶段（II）和脆性破坏阶段（III）。在前期的弹性阶段（I），单轴压缩下裂隙会受到挤压而发生变形，随着上下界面的相对移动，裂隙空间逐渐被挤压，由于裂隙空间较小且挤压速度较快，岩石破坏释放的能量也较少，因此记录释放能量多少的声发射数也会较低；继续加载，释放声发射数开始出现第1 个峰值，说明在复合岩层的局部位置发生破坏，在应力集中的位置开始萌生裂纹，并逐渐沿着最大主应力方向扩展，岩层进入塑性破坏阶段（II）；本次模拟试验除了外边界，还存在圆形内部边界，当裂纹扩展到一定程度会开始集中向边界延伸，扩展到圆形内部边界和外边界时，模型试件发生瞬时破坏并释放很高的能量，应力-应变曲线在峰值后会发生1～3 段骤降，而声发射曲线会骤升达到1～3 个峰值且与应力-应变曲线对应，该阶段破坏较快且岩层破坏程度大，可将此过程看做脆性破坏阶段（III）。值得注意的是应力-应变曲线在峰值后又出现多个小峰值，这表明1 条预制裂隙与内边界或外边界贯通后的复合岩层还有一定的强度，其他裂隙又相继开裂并扩展到边界以致贯通整个模型试件。应力-应变曲线取得峰值后开始陡降时，声发射曲线刚好开始骤升，这是由于模型试件破坏失稳会快速释放能量使得声发射数快速增加，在声发射数-步数曲线中表现为多个峰值。

2.3 裂纹扩展的分形特性

RFPA2D运算可得到裂纹图像，然后对图片进行尺寸处理排除尺寸效应，并进行灰度处理和二值化。在Matlab 的编码过程中，将图像的颜色阈值调整到0.1，使得裂纹部分全部为黑色，其他部分全部为白色。裂纹扩展的灰度图像和二值化图像如图6。

图6 裂纹扩展的灰度图像和二值化图像Fig.6 Gray image and binarized image of crack propagation

盒维数法[15]是利用长度为δi的正方形网格覆盖裂纹图像，得到所需网格数分别为Ni。不断地改变盒子的尺寸得到多组网格数，分形维数与网格数之间的关系为：

式中：Ni、Ni+1为长度为δi、δi+1的网格数；δi、δi+1为网格的长度；D为分形维数。

通过Matlab 拟合得到了不同裂隙倾角和复合岩层倾角对应的双对数曲线，相关度R2均大于0.85，说明含孔多裂隙复合岩层在单轴压缩下得到的裂纹具有分形特征。拟合出的lgN（δ）-lgδ双对数曲线如图7。

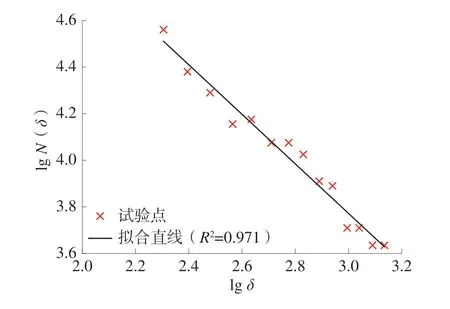
图7 lgN（δ）-lgδ 双对数曲线Fig.7 lgN（δ）-lgδ logarithmic curve

分形维数为拟合直线斜率的负值：

通过式（1）和式（2）计算得到不同裂隙倾角试件裂纹的分形维数-步数曲线，分形维数在整体上随步数的增加而增加，但曲线也会存在多个峰值点，最终范围在1.2～1.4 之间。对比声发射数-步数曲线，发现分形维数曲线中的峰值点总会在声发射曲线峰值点之前，这是由于分形维数会受到盒子尺寸的限制，当裂纹开口较大时，盒子数不会发生变化，分形维数达到峰值，但是裂纹会继续开裂并导致岩层破坏以声发射形式释放能量，所以分形维数对岩层破坏有一定的表征作用。

图4 中模型试件弹性阶段中裂纹出现较少且D趋近于0；初期裂纹会从孔洞最高点和最低点起裂沿着最大主应力方向扩展近似形成1 条近似直线裂纹，α=0°、60°、90°时的初期裂纹分别对应在图5（a）中7～14 步、图5（b）中12～17 步、图5（c）中10～16 步，而在这3 个阶段中的D在1 附近；在岩层脆性破坏阶段，裂纹会演变出次生裂纹，裂纹扩展路径变得越来越复杂，而D也会相应地变大，该结果与彭瑞东等[16]的结论一致。

2.4 岩层倾角（β）对含孔复合岩层的影响

不同岩层倾角下复合岩层破坏模式和声发射图如图8。

图8 不同岩层倾角下复合岩层破坏模式和声发射图Fig.8 Failure model and AE diagrams of composite strata with different dip angles

α=0°不变，改变β=0°、30°、45°、60°、90°，根据裂纹的开裂形式和扩展位置将破坏模式分为2 类：穿切软岩破坏模式（图8（a）、图8（b）、图8（c））和沿软岩破坏模式（图8（d）、图8（e））。

1）当β=0°、30°、45°时，加载初期拉伸裂纹从孔洞的最高和最低点开始沿着最大主应力方向分别向上或向下扩展直至孔洞上下两预制裂隙处；然后对角线处的裂隙两端开始萌生拉伸裂纹和远场裂纹，拉伸裂纹穿过岩层扩展，而远场裂纹沿着软岩层A 扩展；随着加载步数的增加，裂纹在软硬岩层之间穿插，最终导致模型试件整体失稳。

2）当β=60°、90°时，拉伸裂纹从圆孔最高和最低点处开裂并沿着软岩层不断扩展，在拉伸裂纹接近模型边界时，对角线处裂隙开始沿着软岩层A 产生裂纹并沿着该岩层不断扩展；与此同时，其他软岩层内开始出现远场裂纹；部分拉伸裂纹沿着软岩层临近边界衍生出剪切裂纹，裂纹与边界贯通，模型试件发生失稳破坏。

3 α 和β 对峰值抗压强度的影响

改变α和β得到多种不同的模型试件，然后根据应力-应变曲线得到峰值抗压强度（σ），不同α和β模型试件的抗压强度如图9。

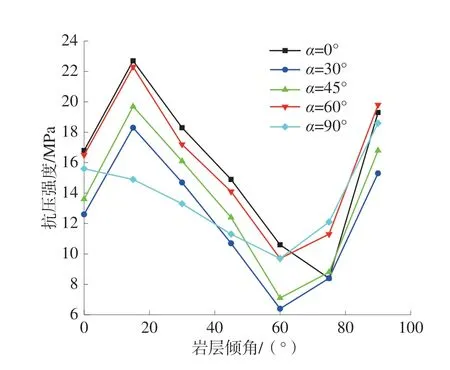
图9 不同α 和β 模型试件的抗压强度Fig.9 Compressive strength of specimens with different α and β models

α=0°、30°、45°、60°时的σ变化趋势相同，均为先增大后减小再增大；β=15°时σ取得最大值，最小值在β=60°取得（α=0°时最小值在β=75°），该结论与文献[17]的研究结果一致；α=90°时σ随着β的变化先减小再增大，并在β=60°时取得最小值；β＜60°时，α=0°的σ比其他α对应的σ都大；所有模型试件的σ最大值在α=0°、β=15°时取得，最小值在α=30°、β=60°时取得；β=0°、15°、30°、45°、60°、75°、90°时，σ随着α改变涨幅分别为33.3%、52.3%、37.6%、31.9%、65.6%、44%、29.4%；α=0°、30°、45°、60°时，σ随着β改变涨幅最大为186%、最小为91.8%。因此，岩层倾角对含孔洞复合岩层的抗压强度影响更大。

4 分形维数量化分析

不同α、β模型试件裂纹的分形维数见表2。

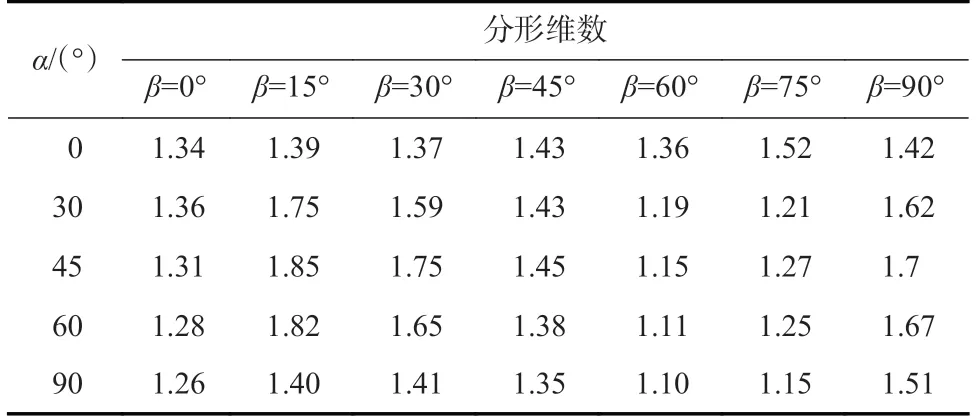
表2 不同α、β 模型试件裂纹的分形维数Table 2 Fractal dimension of cracks in specimens with different α and β models

由表2 可知：分形维数值的变化范围为1.10～1.85，符合彭瑞东等[16]的结论；当α=0°时分形维数的变化不是很明显，增幅最大为13.4%；当α=30°、45°、60°、90°时，分形维数的增幅均超过35%，随着β的变化分形维数先增大后减小再增大，其变化规律与抗压强度相似。

当α=30°、45°、60°时，将不同的β模型试件对应的D和σ模拟试验点绘制在图中并拟合（图略），发现拟合直线的相关度R2均大于85%，所以它们具有高度的线性关系。σ会随着D的增加而增大，这是由于强度越高的岩层在受压破坏时会释放越多能量，其中一部分能量会以裂纹的形式释放，且耗散能量与分形维数呈正比[18]，那么裂纹的数量增多且路径越来复杂，就会导致D相应地增加。将模拟试验点拟合与文献[14]中物理试验点拟合得到的公式进行对比，发现模拟试验和物理试验中σ与D均呈正比例关系，拟合直线的变化率差别为8.4%～9.57%，证明了模拟结果的有效性。

5 结语

通过RFPA2D数值试验研究了在单轴压缩下含孔多裂隙复合岩层的破坏模式和裂纹扩展机制，并运用分形理论量化了裂纹的分形特征。

1）岩层倾角为0°时，改变裂隙倾角可将含孔复合岩层破坏模式分为2 类：X 型破坏模式和Y型破坏模式。不同裂隙倾角的岩层模型对应的应力-应变曲线出现陡降时，声发射数会相应地骤增，声发射曲线可以很好地解释岩石破坏过程中的能量变化。声发射曲线峰值大多出现在分形维数曲线峰值之后，说明分形维数对复合岩层破坏有一定的表征作用。

2）裂隙倾角为0°时，改变岩层倾角对应含孔复合岩层的破坏模式可分为2 类：穿切软岩破坏模式和沿软岩破坏模式。由应力-应变曲线可知：β=0°～90°，抗压强度的涨幅范围为91.8%～186%；α=0°～90°，抗压强度的涨幅范围为29.4%～65.6%。因此岩层倾角对含孔洞复合岩层的破坏影响更大。

3）α=30°、45°、60°时，模型试件裂纹的分形维数与抗压强度随着岩层倾角的变化规律一致，将试验点拟合发现D与σ存在较强的正相关关系（R2＞0.85），拟合得到的关系式分别为σ=18.81D-14.9（R2=0.932）、σ=15.58D-9.82（R2=0.884 8）、σ=15.77D-7.04（R2=0.851 8）。