外肢体机器人驱动单元低速死区自适应补偿方法

陈重远 陈珂 刘浩 欧阳小平

摘要：为提高外肢体机器人高功率密度驱动单元的控制精度，提出一种低速死区自适应补偿方法。首先基于最小二乘系统辨识与阻尼辨识方法建立驱动单元模型，然后提出驱动单元的计算力矩控制方法，最后提出驱动单元的低速死区自适应补偿方法，并进行了实验验证。研究结果表明，与传统PID控制方法相比，采用计算力矩控制方法后驱动单元最大角度跟踪误差减小了约53%，平均角度跟踪误差减小了约38%；在计算力矩控制方法的基础上，采用低速死区自适应补偿方法后，驱动单元最大角度跟踪误差减小了约45%，平均角度跟踪误差减小了约60%，驱动单元的控制精度得到了显著提高。

关键词：驱动单元；死区补偿；控制方法；外肢体机器人；系统辨识

中图分类号：TP182

DOI：10.3969/j.issn.1004132X.2024.01.005

Low-speed Dead Zone Adaptive Compensation Method for Drive Units of

Supernumerary Robotic Limbs

CHEN Zhongyuan1，2 CHEN Ke1，2 LIU Hao1，2，3 OUYANG Xiaoping1，2

1.School of Mechanical Engineering，Zhejiang University，Hangzhou，310027

2.State Key Laboratory of Fluid Power and Mechatronic Systems，Hangzhou，310027

3.Institute of Advanced Technology，Zhejiang University，Hangzhou，310027

Abstract： To improve the control accuracy of high power density drive units in supernumerary robotic limbs， a low-speed dead zone adaptive compensation method was proposed. Firstly， the drive unit model was established based on the least square system identification and damping identification methods. Then， a computed torque control method for the drive units was proposed. Finally， an adaptive compensation method for the low-speed dead zone of the drive units was proposed and verified. The experimental results show that compared with the traditional PID control method， the maximum angle tracking errors of the drive units are reduced by about 53% and the average angle tracking errors are reduced by about 38% after the computed torque control method is utilized. Based on the computed torque control method， the maximum angle tracking errors of the drive units are reduced by about 45% and the average angle tracking errors are reduced by about 60% after the low-speed dead zone adaptive compensation method is adopted. The control accuracy of the drive units is significantly improved.

Key words： drive unit; dead zone compensation; control method; supernumerary robotic limbs; system identification

0 引言

外肢體机器人泛指一类带有一个或多个自主运作机械臂并用于辅助人体进行多工况作业的机器人［1］，它可以不需要人类肢体引导就独立完成特定工作任务，在工厂作业、日常生活辅助、紧急救援等领域具有广阔的应用前景。近年来，国内外学者对外肢体机器人进行了广泛研究。

驱动单元指能够为机器人提供扭矩输出的机械结构或机械组件，是外肢体机器人的核心部件之一，决定了机器人的输出性能上限。驱动单元一般由电机、减速器和驱动器三个部分组成，目前主要有两种主流类型［2-3］，一种是高转速永磁内转子伺服电机搭配大减速比谐波减速器，另一种是外转子电机搭配内嵌行星减速器。尽管第二种类型存在输出回差大等缺点，但总体特性更符合外肢体机器人的实际应用需求，且对机器人的结构布置包容性更强。因此，本文的研究对象是第二种类型的高功率密度驱动单元。

在实际应用过程中，驱动单元控制存在低速死区问题，即驱动单元在低速区域，尤其是速度零点附近，控制精度较差。低速死区形成的主要原因包括：部件加工精度影响、三相逆变器死区影响［4-5］、永磁同步电机齿槽波动力矩和电磁波动力矩影响［6］、低速下驱动单元传动过程中非线性摩擦转矩影响［7］等。

目前，驱动单元的死区补偿方法主要有两种：①优化三相逆变方式，改善电流环。在驱动器磁场定向控制（FOC）的电流内环进行补偿，通过在相电流过零点附近添加可变电流带、加入相电流阈值等方式抑制低速反电动势高次谐波，从而提高驱动单元电机的低速稳定性［5］。该方法的优点是可以显著抑制反电动势振荡，提高电机低速控制性能，但缺点是需要对三相逆变器底层控制逻辑作出修改，且具有一定程度的硬件依赖性，更换不同的设备后往往不能取得最佳补偿效果。②进行摩擦补偿，抑制非线性摩擦力矩影响。具体包括基于摩擦模型的补偿方法和不基于摩擦模型的补偿方法。前者需要观测状态变量并依据辨识模型给出力矩补偿，本质上是一种前馈控制。后者可细分为高增益控制、高频抖动补偿、脉冲补偿等［7］，都是通过在较短时间尺度上对控制量进行大幅修正来达到补偿目的。

外肢体机器人高功率密度驱动单元润滑状态存在时变且动摩擦个体差异明显的特征，不适合通过单一的精确摩擦模型进行补偿。同时，高频冲击类补偿会显著缩短减速器齿面接触疲劳寿命。因此，本文提出了驱动单元的低速死区自适应补偿方法。具体地，首先对外转子电机与行星减速器进行建模，采用最小二乘系统辨识方法获得驱动单元空载开环拟合传递函数。然后，通过实验测量获得驱动单元简化线性负载的阻尼模型，建立前馈反馈控制机制，提出驱动单元的计算力矩控制方法。最后，提出低速死区自适应补偿方法提高驱动单元的控制精度。

1 高功率密度驱动单元

1.1 应用对象

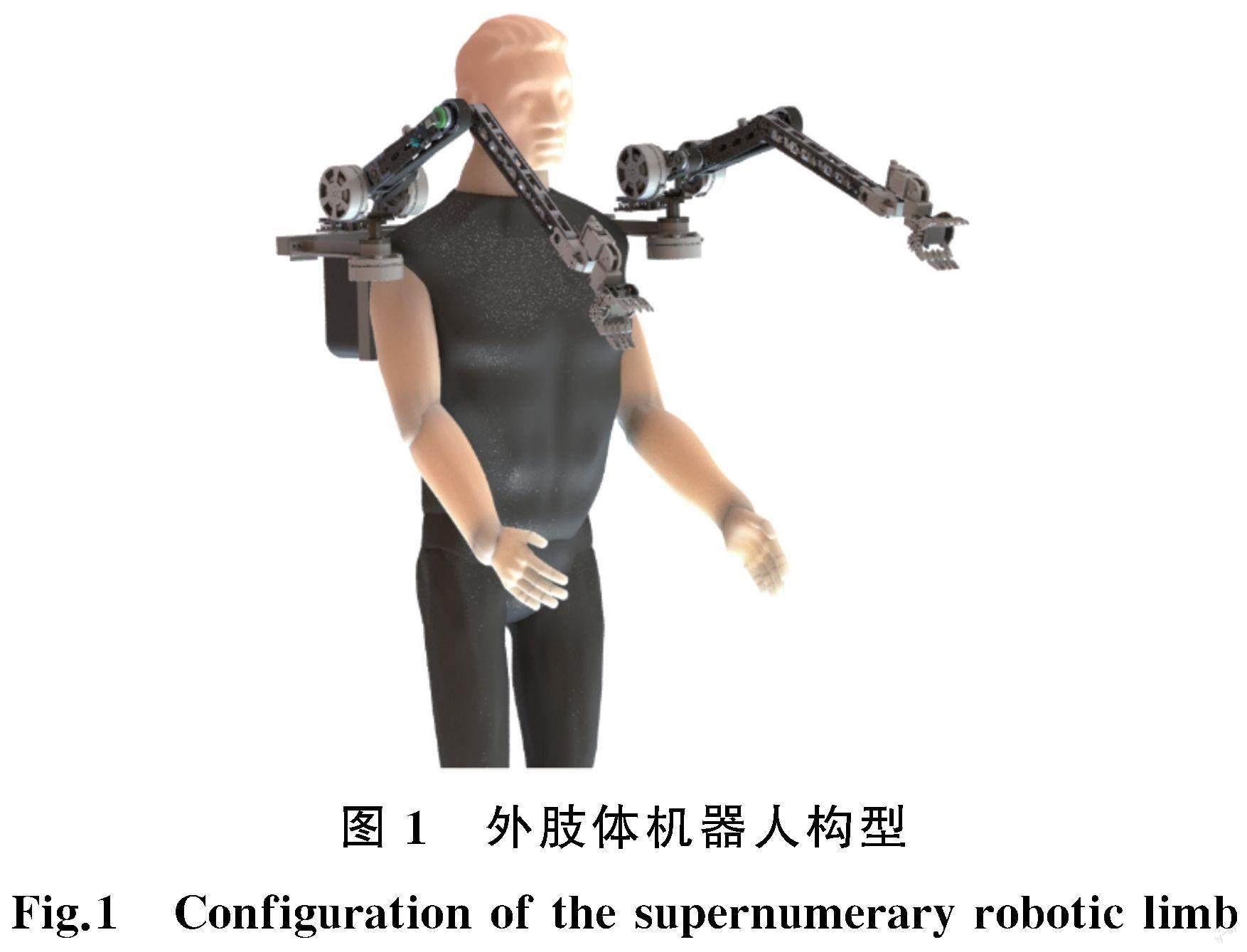
本文研究的驱动单元应用于由两条三自由度串联机械臂与末端执行器构成的外肢体机器人上，如图1所示。该外肢体机器人的目标应用场景为工业装配生产线。

1.2 驱动单元结构

为了实现外肢体机器人低速大扭矩输出以及高精度运动控制的目标，驱动单元选择了中小减速比两级行星减速器搭配小长径比高扭矩外转子永磁同步电机的设计方案，其结构如图2所示。

该驱动单元中减速器的单级减速比为4.4，多级减速比为19.36。在电机额定转速下，驱动单元的功率密度高达360 W/kg，能够满足外肢体机器人的应用需求，驱动单元实物如图3所示。

2 高功率密度驱动单元建模

分别对驱动单元中的外转子永磁同步电机和两级行星减速器进行建模，在此基础上建立驱动单元模型并进行系统辨识。

2.1 外转子永磁同步电机模型

永磁同步电机的三维结构如图4所示。该电机为42极36槽外转子表贴式凸极转子结构永磁同步电机，每极每相槽数为4/7，计算得到电机绕组系数为0.904，较大的绕组系数表明电机具有较大的输出扭矩［8］。

永磁同步电机是强耦合非线性变参数系统，其精细化建模非常复杂且计算负担重，在实际电机特性分析过程中，往往需要对电机模型进行适度简化。

通过机电能量法获得电机扭矩公式如下：

式中，pn为电机极对数；iq为电机q轴电流；id为电机d轴电流；Lq为电机q轴电感；Ld为电机d轴电感；ψf为电机磁链（ψf=0.0035 Wb）。

将id = 0与电机磁链数值代入式（1）可得电机理论扭矩公式如下：

Te=0.22iq（2）

由于驱动单元中电机与转子分别直接连接减速器且电机本身无轴承等固体摩擦支撑件，因此电机转动阻力仅需考虑空气黏滞阻尼项。此时，电机输出的机械运动方程为

式中，ωm为电机机械角速度；Jm为电机转子转动惯量；Te为电机电磁扭矩；TB为电机转子空气阻尼力矩；Tout为電机输出扭矩。

假设电机转子外壁空气速度始终等于转子速度，且实验空间空旷半径大于等于2 m，可进一步采用牛顿黏滞定律［9］对空气阻尼力矩进行估计如下：

式中，η为实验室环境空气黏滞系数；de为转子外径；ωe为转子角速度；Le为转子长度；Lt为实验空间空旷半径，本文取值为2 m。

经计算，在额定转速为1350 r/min时，电机转动黏滞阻尼力矩约为8.68×10-7N·m。这个数量级的空气阻尼几乎不会对电机的运动造成干扰，故可以忽略。因此，电机的转子动力学模型可进一步简化为

2.2 两级行星减速器模型

行星减速器的三维结构如图5所示，该减速器被包含在永磁同步电机定子内部。驱动单元的机械负载主要来自减速器内齿轮和行星架的惯性负载以及12处齿轮啮合、6处滑动接触和2处滚动轴承接触。减速器的主要阻尼包括线性黏滞阻尼、流体阻尼、库仑摩擦阻尼、滞后阻尼和结构阻尼等。

KAHRAMAN［10］、鲍和云［11］和莫文超［12］对行星减速器的纯扭转动力学建模如下：

为了简化模型，本文将减速器零件视为刚度无穷大的刚体，进而忽略形变形成的阻尼项，默认转动惯量为绕质心的转动惯量，可获得如下动力学模型：

式中，i为行星减速器的单级减速比；JFS为第一级太阳轮及输入法兰的转动惯量；ωFS为第一级太阳轮的转动角速度；JSS为第二级太阳轮及第一级行星架的转动惯量；ωSS为第二级太阳轮的转动角速度；JSH为输出法兰的转动惯量；ωSH为输出法兰的转速；JmPn为第n级行星轮绕瞬心转动时的转动惯量；ωPn为第n级行星齿轮的合成运动角速度；TL为减速器的负载扭矩；Tf为减速器的库仑摩擦扭矩；Tin为减速器的输入扭矩；BRe为减速器的阻尼系数；sgn（ωFS）为符号函数，其正负性随运动状态改变。

减速器行星齿轮的复合运动可以分解为绕定轴旋转的牵连运动和绕动轴旋转的相对运动，其合成运动角速度ωPn等于相对角速度ωrn与牵连角速度ωHn的差值，即ωPn = ωrn - ωHn。如图6所示，点C为行星轮的运动瞬心，该点位置满足：

式中，vCHn为行星齿轮运动瞬心的牵连速度；vCrn为行星轮运动瞬心的相对速度；O1为定轴轴心；O2为动轴轴心;lO1O2为O1到O2的长度，其他同类符号含义类此。

减速器行星架的牵连角速度ωHn与定轴轮系下行星齿轮转动的相对角速度ωrn可分别按照如下公式进行计算：

式中，Zp为行星轮齿数；Zs为太阳轮齿数。

依据转动惯量的平行轴定理［13］，每个行星齿轮绕瞬心旋转的转动惯量JmPn为

式中，JPn为行星齿轮绕质心的转动惯量；mPn为行星齿轮质量。

减速器的空载模型为

式中，Jrecal为行星减速器的总转动惯量。

2.3 驱动单元模型

结合电机扭矩系数km与式（12），驱动单元空载条件下的模型为

式中，Jtotal为总转动惯量，且Jtotal = Jm+ Jrecal；I为电机q轴电流值。

在式（13）的基础上增加负载项与负载摩擦项，获得驱动单元在负载条件下的模型如下：

式中，CL为负载阻尼系数。

忽略初始阻尼项后，通过拉普拉斯变换获得驱动单元在空载条件下的理论传递函数为

2.4 驱动单元系统辨识及特性分析

尽管获得了驱动单元在空载条件下的一阶理论传递函数，但式（15）中符号函数sgn（ωFS）的正负性会随运动状态改变，并且在实际应用中减速器的阻尼变化与润滑脂液化状态、输出绝对角度、减速器组件精度、减速器组件刚度均有关联，系数存在时变，模型并非严格线性，因此，需要进一步通过系统辨识方法［14］来获得驱动单元的最佳拟合傳递函数。

由于外肢体机器人实际运行过程中，驱动单元运行速度的最大值不超过180°/s，关节完成单一动作的作动频率不超过15 Hz，因此，系统辨识实验选择频率范围为0.1～15 Hz、最大幅值为209°的正弦曲线作为目标输入。辨识实验时间共30 s，控制频率为500 Hz，共计15 000个数据点。

由于被辨识的系统需要具有稳定性，因此在驱动单元控制环节加入了比例控制，在不改变系统阶数的情况下使系统构成闭环，如图7所示。

系统辨识过程中闭环系统的部分目标输入与实际响应如图8所示。

采用最小二乘辨识方法获得该系统的1阶、2阶、3阶、4阶模型，拟合结果如图9所示。可以看出，2阶模型与1阶模型的拟合度最佳。其中，1阶拟合传递函数平均拟合误差为0.1594 rad/s，2阶传递函数平均拟合误差为0.1591 rad/s，3阶传递函数平均拟合误差为0.1625 rad/s，4阶传递函数平均拟合误差为1.4622 rad/s。从拟合出的传递函数可知，2阶模型零极点位置与1阶模型类似。

其中1阶传递函数为

2阶传递函数为

本文以上述拟合结果为依据，通过零极点配置的方法可以获得驱动单元的最优控制参数。

2.5 驱动单元负载阻尼辨识

负载阻尼辨识是为了建立驱动单元的线性简化负载摩擦模型，并为控制环节的前馈量设定提供依据。驱动单元的负载实验系统如图10所示。驱动单元外侧装有绝对值关节编码器用于反馈运动信息。实验数据由CAN总线汇集，并以UDP数据包的形式通过控制器节点与上位机建立的以太网有线连接进行上传。其中，连杆自身质量为538 g，连杆质心距离转动中心的距离为216 mm，负载质量为3 kg，负载质心距离转动中心的距离为334 mm。

为了获得驱动单元的负载阻尼特性，实验过程中控制驱动单元匀速转动，使连杆与负载的重力垂直分量引起的重力负载转矩以及负载阻尼转矩始终与驱动单元输出转矩平衡，分别测量出不同负载转矩下驱动单元负载阻尼转矩的大小。如图11所示，驱动单元以不同方向同一速度匀速转过同一角度时，驱动单元输出转矩差值为两倍的负载阻尼转矩（图中，Tdrive-unit为驱动单元输出转矩；G为负载所受重力）。

在不同转速下，驱动单元输出端负载转矩Tload（4～11 N·m）与驱动单元电机侧负载阻尼转矩Tfe的关系如图12所示。

由于实验中驱动单元的输出角加速度不能精确控制为零，且驱动单元在不同位置润滑与啮合情况不同，因此图12中由驱动单元电机q轴电流换算得到的负载扭矩存在波动。由图12可知，驱动单元在不同转速下的负载阻尼转矩处于相近分布范围，且与负载扭矩成近似线性关系。

根据拟合结果，本文中驱动单元的负载阻尼转矩特性可近似表示为

Tf=0.0295TL+0.035（18）

负载阻尼系数CL为

CL=0.0295i2=0.571（19）

在摩擦力作用下，驱动单元输出端每承受1 N·m负载，可等效为无摩擦负载1.571 N·m，负载效率为63.7%。

3 高功率密度驱动单元控制

3.1 PID控制

驱动单元PID控制框图见图13，包含了电流环、速度环、位置环的控制。本文将PID控制方法作为基准对比方法。

在离散系统中，PID控制模型可表示为

式中，u（k）为PID输出量；e（k）为输入误差量；KP为比例系数；KI为积分系数；KD为微分系数；k为周期总数；T为控制周期。

3.2 计算力矩控制

计算力矩控制方法［15］以被控系统的动力学模型为基础，通过加入位移反馈、速度反馈和加速度前馈得到响应控制律，并通过在内控制回路中引入非线性补偿，使被控系统转化为易于控制的线性定常系统。

图10所示的机器人关节负载试验系统的动力学模型为

在计算力矩控制实验中，驱动单元的角度跟踪效果如图15所示，角度跟踪误差如图16所示，电机q轴电流变化如图17所示。

采用计算力矩控制方法后，驱动单元的最大角度跟踪误差约为2.876°，平均角度跟踪误差约为0.847°。相比于PID控制方法（最大角度跟踪误差约为6.114°，平均角度跟踪误差约为1.369°），计算力矩控制方法的精度有明显提高，最大角度误差下降了约53%，平均角度误差下降了约38%。同时，驱动单元电机q轴电流的振颤现象得到了有效抑制。但可以发现，驱动单元在低速换向时仍然存在死区问题，需要进行死区补偿。

4 高功率密度驱动单元低速死区自适应补偿

通过控制实验可以发现，驱动单元在大负载条件下进行换向操作时存在明显的低速死区现象，具体表现为：在转速接近零时驱动单元会提前停止或启动滞后，导致输出角度无法精确跟踪目标角度，如图15所示。

4.1 低速死区自适应补偿方法

本文提出的驱动单元的低速死区自适应补偿方法在驱动单元运行时，根据实时角度跟踪误差与转速判断是否处于低速死区，并在死区内进行电机q轴电流补偿。低速死区的判别原理如图18所示，根据两个条件判断驱动单元是否存在低速死区：①驱动单元的角度误差是否会超过阈值；②驱动单元转速是否换向。

驱动单元处于低速死区时， q轴电流补偿公式如下：

其中，Icomp为补偿电流值， θtran为目标轨迹的换向角度，θ1为死区自适应补偿的介入角度，θ为驱动单元实时角度，I1为电机q轴补偿电流的初始值，I2为电机q轴补偿电流的最终值，其原理如图19所示。参数θ1、I1、I2的值直接决定了驱动单元死区补偿的效果，而三个参数值的选择依赖于自适应迭代优化算法。

具体地，本文提出的低速死区自适应补偿方法包含三个步骤：

（1）参数初始值与调节范围的确定。根据经验、驱动单元性能和实验测试数据，设定参数θ1、I1、I2的初始值，并确定各个参数的调节范围。

（2）模糊推理系統的建立。基于参数θ1、I1、I2的初始值与调节范围，建立用于三个参数优化调节的模糊推理系统，将实验测试获取的最大角度跟踪误差作为输入，经过模糊化、模糊推理和去模糊化处理后，输出参数θ1、I1、I2的调节量k。其中，根据驱动单元最大角度跟踪误差越大，参数I1、I2的值越大，θ1越远离θtran的原则，建立模糊规则。

（3）参数的迭代优化。在参数θ1、I1、I2的迭代优化过程中，每一次迭代都需要将前一个测试周期中驱动单元最大角度跟踪误差作为模糊推理系统的输入，输出为参数θ1、I1、I2调节后的值，θ1←θ1-kθ1，I1←I1+kI1，I2←I2+kI2。此处值得注意的是，如图20所示，若当前死区类型为反向死区，则模糊推理获得的参数调节量k需减半；若当前死区类型为双向死区，则调节量直接取前两次测试周期获得的调节量平均值，并在下一测试周期完成后，基于最大角度跟踪误差从最近三个测试周期中选取最佳的参数值组合。本文提出的死区自适应补偿方法的流程如图21所示。参数θ1、I1、I2依据调节量k变化的过程即为自适应迭代优化的过程。

图22显示了在计算力矩控制方法下，采用低速死区自适应补偿方法后驱动单元的角度跟踪效果与电机q轴电流变化情况。图22c中黄色阴影内的黑色曲线为进行死区补偿后的电机q轴电流变化曲线，绿色曲线为未进行死区补偿的电机q轴电流变化曲线。在进行死区补偿后电机q轴电流出现了一次明显的线性阶跃，后续由于计算力矩控制的反馈补偿作用，电机q轴电流逐渐又被拉回补偿前的水平，驱动单元在死区内的角度跟踪误差得到了明显的改善。

4.2 低速死区自适应补偿实验

4.2.1 参数初始值与调节范围

根据经验、驱动单元性能和实验测试数据，设定参数θ1、I1、I2的初始值分别为θ1=70°、I1=2 A、I2=1 A。进一步，确定参数θ1的初始调节量为10°，参数I1和I2的初始调节量分别为2 A和1 A。

4.2.2 模糊推理系统

基于参数θ1、I1、I2的初始值与调节范围，对模糊推理系统输入变量最大角度跟踪误差进行模糊化处理，如表1所示。在本文的实验中，未进行死区自适应补偿时，驱动单元的最大角度跟踪误差约为2.9°。因此，本文将模糊推理系统输入变量的范围设定为［-3，3］，并划分为5个集合：负大（NB）、负小（NS）、零（ZO）、正小（PS）、正大（PB）。

类似地，模糊推理系统的输出变量同样被分为5个集合：负大（NB）、负小（NS）、零（ZO）、正小（PS）、正大（PB），如表2所示。

根据驱动单元最大角度跟踪误差emax越大，参数I1、I2的值越大，θ1越远离θtran，k值越大原则建立模糊规则如下：

（1）若emax为NB，则k为NB；

（2）若emax为NS，则k为NS；

（3）若emax为ZO，则k为ZO；

（4）若emax为PS，则k为PS；

（5）若emax为PB，则k为PB；

模糊推理系统的输出变量u可由emax与模糊关系矩阵R进行计算获得：

u=emax R（24）

其中，模糊关系矩阵R为

4.2.3 参数迭代优化

在建立模糊推理系统后，即可进行参数θ1、I1、I2的自适应迭代优化。如图23所示，按照参数θ1、I1、I2的初始值进行死区补偿后，最大角度跟踪误差为2.04°，隶属于PS与PB集合，模糊推理系统的输出可表示为

根据重心法进行去模糊化计算，并对uPS和uPB求平均后乘以接近1的随机比例系数（为了给相对公式化的模糊控制提供随机变动空间以求结果相对多样）获得参数调节量的变化倍率为2.08，本次迭代获得的参数调节量k=2.08，参数θ1、I1、I2的变化量如下：

经过第一次迭代优化后，参数θ1、I1、I2的值分别为49.2°、6.16 A和3.08 A，如图23所示。在下一个测试周期中采用以上参数值进行死区补偿后，最大角度跟踪误差为0.78°，隶属于PS和ZO集合，模糊推理系统的输出可表示为

再次根据重心法进行去模糊化计算，并对uPS和uZO求平均后乘以接近1的随机比例系数获得参数调节量的变化倍率为0.73，本次迭代获得的参数调节量k=0.73，参数θ1、I1、I2的变化量如下：

经过第二次迭代优化后，参数θ1、I1、I2的值分别为41.9°、7.62 A和3.81 A，如图23所示。采用以上参数值进行死区补偿后，最大角度跟踪误差为0.84°。同时，死区补偿后的最大反向跟踪误差为-0.34°，说明死区补偿过度，该次测试周期的死区为双向死区。选择前两次测试周期中参数θ1、I1、I2的平均值作为本次迭代获得的参数值，分别为45.6°、6.89 A和3.45 A。采用以上参数值进行死区补偿后，对比最近三个测试周期的补偿效果，基于最大角度跟踪误差从最近三个测试周期中选取最佳的参数值组合，为49.2°、6.16 A和3.08 A。

采用最佳的参数值组合进行死区补偿后，驱动单元的角度跟踪结果如图24所示。低速死区补偿后的驱动单元最大角度跟踪误差约为1.573°，仅有未进行死区补偿前最大角度跟踪误差的54.5%，且最大角度跟踪误差出现在死区补偿开始介入的时刻。低速死区补偿后的驱动单元平均角度跟踪误差约为0.335°，仅有未进行死区补偿前平均角度跟踪误差的39.6%。

5 结论

（1）提出了一种外肢体机器人用高功率密度驱动单元的参数辨识与建模方法，并进行了控制验证。基于阻尼辨识方法建立了驱动单元负载阻尼特性模型，提出了基于动力学模型的计算力矩控制方法。实验结果显示，在采用基于动力学模型的计算力矩控制方法时，驱动单元最大角度跟踪误差相较于PID控制方法减小了约53%，平均角度跟踪误差减小了约38%。

（2）针对驱动单元控制的低速死区问题，提出了一种低速死区在线自适应补偿方法。实验结果显示，在计算力矩控制方法的基础上采用死区自适应补偿方法，驱动单元最大角度跟踪误差相较于死区补偿前减小了约45%，平均角度跟踪误差减小了约60%。实验结果验证了死区自适应补偿方法在外肢体机器人驱动单元控制上的有效性。未来，将针对驱动单元即时死区补偿开展研究，以便于更快地适应多变工况。

参考文献：

［1］ 荆泓玮， 朱延河， 赵思恺， 等. 外肢体机器人研究现状及发展趋势［J］. 机械工程学报， 2020， 56（7）：1-9.

JING Hongwei， ZHU Yanhe， ZHAO Sikai， et al. Research Satus and DevelopmentTrend of Supernumerary Robotic Limbs［J］. Journal of Mechanical Engineering， 2020， 56（7）：1-9.

［2］ KATZ B， CARLO J D， KIM S. Mini Cheetah：a Platform for Pushing the Limits of Dynamic Quadruped Control［C］∥IEEE International Conference on Robotics and Automation （ICRA）. Montreal， 2019：6295-6301.

［3］ PARIETTI F， CHAN K， ASADA H H. Bracing the Human Body with Supernumerary Robotic Limbs for Physical Assistance and Load Reduction［C］∥IEEE International Conference on Robotics and Automation （ICRA）. Seattle， 2014：141-148.

［4］ 李长磊. 永磁同步电机低速控制研究［D］.合肥： 中国科学技术大学， 2016.

LI Changlei. Research on Low Speed Control of Permanent Magnet Synchronous Motor［D］. Hefei：University of Science and Technology of China， 2016.

［5］ 刘青. 永磁同步电机无传感器性能提升实现及死区补偿［D］.武汉： 华中科技大学， 2019.

LIU Qing. Sensorless Performance Improvement and Dead-time Compensation of Permanent Magnet Synchronous Motor［D］. Wuhan：Huazhong University of Science and Technology， 2019.

［6］ 刘洪玉. 转台伺服系统低速性能分析与摩擦补偿研究［D］. 哈尔滨：哈尔滨工业大学， 2006.

LIU Hongyu. Low-speed Performance Analysis and Friction Compensation Research of Turntable Servo System［D］. Harbin： Harbin Institute of Technology， 2006.

［7］ 郑耿峰. 动态目标仿真轉台控制及摩擦补偿研究［D］. 长春：中国科学院研究生院（长春光学精密机械与物理研究所）， 2011.

ZHENG Gengfeng. Research on Control and Friction Compensation of Dynamic Target Simulation Turntable［D］. Changchun：Graduate School of Chinese Academy of Sciences （Changchun Institute of Optics， Fine Mechanics and Physics）， 2011.

［8］ 徐玉婷. 四足机器人用关节电机设计与分析［D］. 杭州：浙江大学， 2020.

XU Yuting. Design and Analysis of Permanent Magnet Motors for Quadruped Robot［D］. Hangzhou：Zhejiang University， 2020.

［9］ 董艳红， 许震天， 卢颖. 牛顿黏滞定律中黏滞系数两种推导方法［J］.佳木斯大学学报（自然科学版）， 2003，21（3）：323-325.

DONG Yanhong， XU Zhentian， LU Ying. Two Derivation Method of Viscosity Coefficient in Newton's Viscosity Law［J］. Journal of Jiamusi University （Natural Science Edition）， 2003，21（3）：323-325.

［10］ KAHRAMAN A. Natural Modes of Planetary Gear Trains［J］. Journal of Sound Vibration， 1994， 173（1）：125-130.

［11］ 鲍和云. 两级星型齿轮传动系统分流特性及动力学研究［D］. 南京：南京航空航天大学， 2006.

BAO Heyun. Study on Load-split Characteristics and Dynamics of Two-stage Gear Trains［D］. Nanjing：Nanjing University of Aeronautics and Astronautics， 2006.

［12］ 莫文超. 船用汽轮机-行星齿轮减速器轴系动力学特性研究［D］. 哈尔滨：哈尔滨工业大学， 2020.

MO Wenchao. Study on Dynamic Characteristics of Marine Steam Turbing-planetary Gear Reducer Shafting［D］. Harbin：Harbin Institute of Technology， 2020.

［13］ 哈尔滨工业大学理论力学教研室. 理论力学［M］.北京： 高等教育出版社， 1997.

Teaching and Research Section of Theoretical Mechanics of Harbin Institute of Technology. Theoretical Mechanics［M］.Beijing： Higher Education Press， 1997.

［14］ 庞中华， 崔红. 系统辨识与自适应控制MATLAB仿真.［M］. 2版.北京： 北京航空航天大学出版社， 2013.

PANG Zhonghua， CUI Hong. MATLAB Simulation of System Identification and Adaptive Control［M］. 2nd ed. Beijing：Beihang University Press， 2013.

［15］ 霍偉. 机器人动力学与控制［M］. 北京：高等教育出版社， 2005.

HUO Wei. Robot Dynamics and Control［M］.Beijing： Higher Education Press， 2005.