有限元方法在电磁场边界条件教学中的应用

摘""要：电磁场的边界条件是电磁场理论教学中尤为重要的部分，是后续诸多教学内容的基础。然而电磁场在不同材料、不同方向的边界条件各不相同，学生往往难于理解、记忆。用有限元方法设计了带电金属球壳、带电介质球、同轴传输线、波导管、电介质平板波导等几种稳恒电磁场和时谐电磁场模型，展示并讨论了不同情形下电、磁边界条件的特点，使得电磁场边界条件的教学内容更丰富、直观，有助于学生区分和理解不同情形下电、磁边界条件各自的特点，提高教学质量。

关键词：电磁场""边界条件""有限元方法""电磁场理论教学

中图分类号：G642

Application"of"Finite"Element"Method"in"Teaching"Electromagnetic"Boundary"Conditions

FU"Yulan

School"of"Physics"and"Optoelectronic"Engineering，"Beijing"University"of"Technology，"Beijing，"100124"China

Abstract："The"boundary"conditions"for"electromagnetic"fields"are"an"essential"part"of"electromagnetic"field"theory"teaching，"and"they"are"the"basis"of"many"subsequent"teaching"contents."However，"the"boundary"conditions"of"electromagnetic"fields"vary"in"different"materials"and"directions，"making"it"difficult"for"students"to"understand"and"remember."The"finite"element"method"is"used"to"design"several"stable"electromagnetic"field"and"time-harmonic"electromagnetic"field"models，"such"as"charged"metal"spherical"shells，"charged"dielectric"spheres，"coaxial"transmission"lines，"metal"waveguides，"and"dielectric"planar"waveguides."The"characteristics"of"electric"and"magnetic"boundary"conditions"under"different"situations"are"demonstrated"and"discussed，"making"the"teaching"content"of"electromagnetic"field"boundary"conditions"richer"and"more"intuitive，"which"helps"students"distinguish"and"understand"the"characteristics"of"electric"and"magnetic"boundary"conditions"under"different"situations，"and"improves"the"teaching"quality.

Key"Words："Electromagnetic"field;"Boundary"Conditions;"Finite"element"method;"Electromagnetic"field"theory"teaching

电磁场理论是光电信息科学与工程专业及其相近专业的核心课程之一，以“场”的观点讲授电磁运动规律，是后续诸多专业课程的重要基础。电磁场的边界条件是电磁场理论的教学重点与难点，它是后续讲授静态电磁场边值问题，以及电磁波传播中波导管、谐振腔模式求解的必要条件和重要基础。电磁场的边界条件涉及微分方程在几何界面具体化的问题，在不同物理情境下又各不相同，对学生的数学基础和空间想象力有较高要求，在教学中需要一种清晰、具体的方法辅助学生区分记忆。有限元方法是求解电磁问题的有效数值方法[1-2]。将有限元方法应用于电磁场教学中可以直观的展示电磁场各方面的特性[3-4]。本文利用基于有限元方法的COMSOL软件[5]，分别给出静态场和电磁波边界条件的几个模型，以便学生理解不同物理情景下的电磁场各物理量的边界条件。

1""静电场的边界条件

1.1""带电金属球壳的电场边界条件

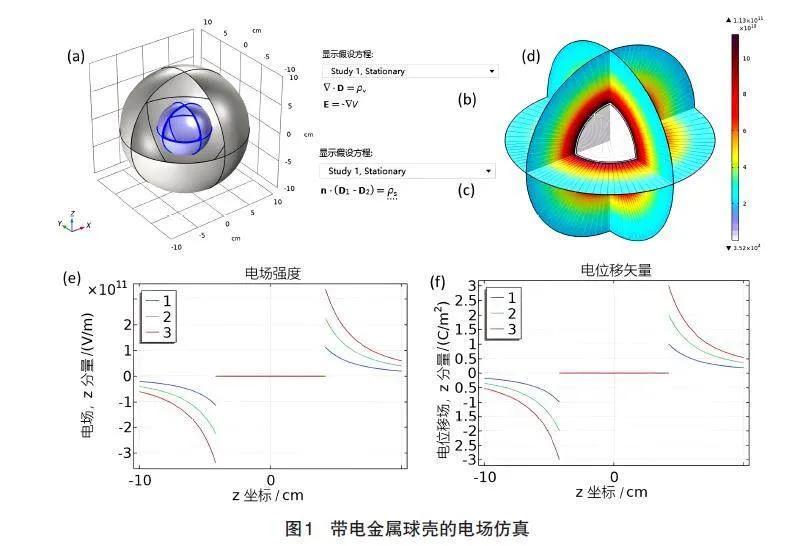
在几何中建立半径分别为4"cm、4.2"cm、10"cm的3个同心球，它们构成3个域，中间一个域为厚度为0.2"cm的球壳，如图1（a）所示。在材料库中添加空气和铜两种材料，选择球壳材料为铜，球壳内外均为空气。在静电模块的设置菜单“方程”下拉选项中可以看到求解的方程即为电场高斯定理和电场-电势关系方程，如图1（b）所示。在物理场中添加“表面电荷密度”边界条件，从设置菜单中可以看到这一边界条件处理的方程为电位移矢量D的边界条件，如图1（c）所示。设置表面电荷密度ρs为“rho”，并在参数设置中将rho赋值为1。在“图形”界面中，选择“表面电荷密度”边界条件的作用区域为铜球壳外表面。添加“接地”边界条件，选择半径为10"cm的球面接地。为使获得电场的解更为准确，在网格设置中，设置“物理场控制网格”的单元大小为“更细”。在“研究”中求解稳态场。为体现电场分布随电荷密度的变化，在研究中添加参数扫描，扫描rho的取值为1、2、3"（C/m2）。

通过求解即可得到带电金属球壳及其周围环境的电场分布，图1（d）给出了电场模和电场线的空间分布。可以看到在球壳外部电场线垂直于球壳表面放射性发出，电场自球壳向远处逐渐减小。而在球壳内部，电场强度为0，无法正确绘制电场线。在z轴上建立自z=-10"cm至z=10"cm的截线，绘制沿这一截线的电场z分量Ez和电位移矢量z分量Dz的分布曲线，分别如图1（e）和图1（f）所示。可以看到，电场强度和电位移矢量分布规律相似，在金属球壳外表面均不连续，在球壳外部向远处衰减，在球壳内部为0。从图1（f）中还可看出，球壳外表面电位移矢量大小的阶跃值恰为参数扫描所设置的面电荷密度rho的取值，即满足图1（c）所示的金属界面电位移矢量的边界条件。而此时E和D的x、y分量均为零，即金属球壳表面切向电场为零，电场方向沿球壳表面法相。可以选择其他截线或界面进行验证和展示。

1.2""电介质球的电场边界条件

在几何中建立半径分别为4"cm、10"cm"的两个球。在材料中添加空气和云母，并选择半径4"cm的球为云母，其外部为空气。在静电模块中添加空间“空间电荷密度”域条件，设置电荷密度为“rho”，并选中云母球区域。在设置中可以看到此条件对应的方程为电场的高斯定理。注意，这里rho的单位不同于上一节，为C/m3。同样对rho进行1-3"（C/m3）的参数扫描。添加“接地”边界条件，另外部大球表面接地。网格的设置与上一节相似。

通过求解得到均匀带电云母球的电场分布。在球的外部，电场线垂直于球面，电场向远处衰减，这与金属球壳类似。不同的是，电场是由球心发，球内部电场强度不为零。同样沿z轴做z=-10"cm到z=10"cm的截线。可以看到，在云母球外表面电位移矢量法向连续和电场强度法向不连续。

2"稳恒磁场的边界条件

2.1"同轴传输线的磁场

同轴传输线是稳恒磁场教学中的常用案例，由于可以认为传输方向无限长，我们只需建立二维模型求解。在几何中分别建立半径为1"cm、3"cm、4"cm、10"cm的同心圆。在材料中添加空气和铜，将半径1"cm的内圆和内径3"cm外径4"cm的圆环设置为铜，构成同轴传输线。其他区域设为空气。采用“磁场”物理场，在设置中可以看到求解的方程为安培光路定理、磁感应强度和磁矢势关系、扩展的欧姆定律。假设同轴传输线内、外层总电流为±1"A，电流密度为总电流与截面面积的比值。添加两个“外部电荷密度”域条件，分别设置内、外层的z方向电流密度为3183.1"A/m2和-545.7"A/m2。网格设置与前文类似。求解后，可以绘制磁场强度H大小“normH”的分布图，可以看出磁场分布在同轴传输线内部，外部磁场为0。建立沿x轴自x=0至x=5"cm的截线，绘制磁场强度y分量Hy沿的分布曲线，可以看出磁感强度在空间始终保持连续。

2.2"有面电流时的磁场边界条件

改变上一节电流密度分布的条件，在上节建立的模型中将两个“外部电流密度”域条件禁用，添加两个“表面电流密度”边界条件，分别选中半径1"cm和半径3"cm的圆，即同轴传输线内层的外表面和外层的内表面。依然假设它们的z方向总电流为±1"A，电流密度为总电流与圆周长的比值，分别为15.92"A/m和-5.31"A/m。在设置中可以看到此条件对应的方程即为有面电流时的磁场边界条件。求解后绘制此时的磁感应强度模的分布图，发现此时磁场只位于内、外导线之间，导线内部磁场为零。

3"电磁波的边界条件

虽然电磁场的边界条件在静态电磁场部分讲授，但在时变电磁场部分仍有重要应用，如求解电磁波的波动方程，下面分别以矩形金属波导管和电介质平板波导为例，考察电磁波在界面处的边界条件。这里应该注意，COMSOL是在频域求解，假定所考察的是单色时谐波，稳态求解器所求解的电磁场是不含时的，即求解复振幅。COMSOL的射频模块和波动光学模块均可仿真电磁波，为方便比较波长和波导尺寸的关系，这里采用波动光学模块。

3.1"波导管

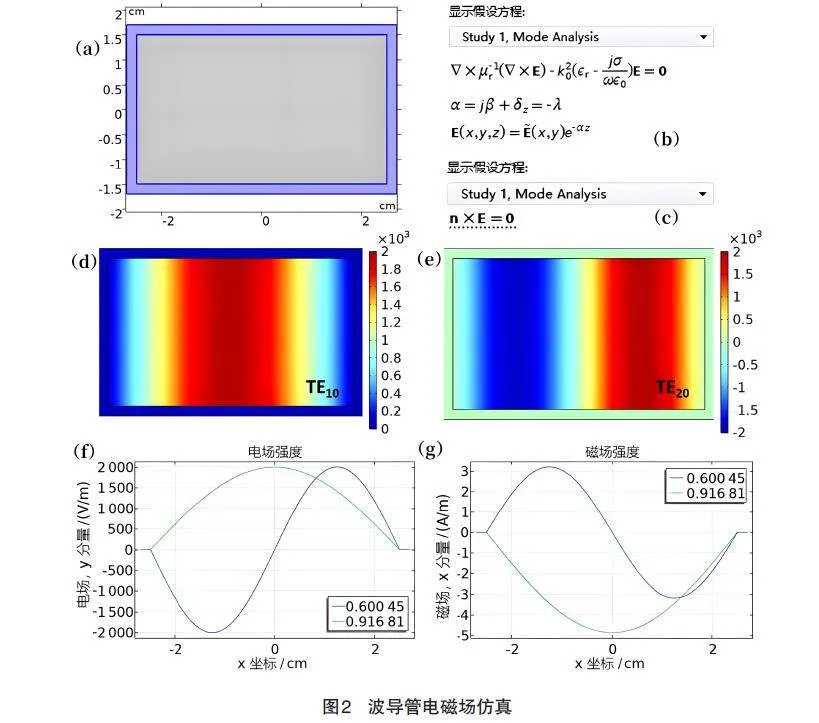
在几何中建立长、高分别为5"cm和4"cm的矩形，作为波导管的内表面；建立长、高分别为5.4"cm和5.4"cm的矩形，和前一矩形共心，作为波导管的外表面。波导管壁厚0.2"cm。在材料中添加空气和铜，将波导管壁设为铜，其内部为空气，如图2（a）所示。金属外部电磁波衰减为0，因此不需要设置外部环境。选择“电磁波，频域”物理场，从设置中可以看到此时求解的方程即为电磁场的波动方程，如图2（b）所示。添加“理想电导体”边界条件，选中波导管内表面，从设置中可以看到此条件对应的方程正为导体的电场边界条件，如图2（c）所示。求解电磁波时的网格大小一般为波长的1/10～1/5，由于趋肤效应，电磁场只在金属表面很小的范围内存在，因此金属表面附近的网格需要进一步细化。这里将波导管内表面上的网格尺寸最大值设为0.1"cm，其他区域设为0.2"cm。在“研究”中添加“模式分析”步骤，求解波长为4"cm的电磁波在波导管中各模式的有效折射率。设置求解有效折射率在1附近的5个模式。

求解得到有效折射率分别为0.916"81、0.745"72、0.629"37、0.629"36、0.600"45，分布对应TE10、TE01、TE11、TM11、TE20"这5个模式，这也是这一波长的电磁波在该波导中能存在的所有模式。考虑到各模式电磁场各分量数量级的差异，这里以TE10和TE20两个模式为例进行讨论，其电场的y分量Ey空间分布分别如图2（d）和图2（e）所示，可以看出TE10模式在波导管中有一个半波分布，而TE20模式在波导管中有正负两个半波分布。沿波导x轴自x=-2.7"cm至x=2.7"cm做截线，图2（f）和图2（g）分别为沿这一截线Ey和Hx的分布曲线。可以看到：Ey在波导管x方向的两个表面上为零，满足切向电场为零的边界条件；Hx在这两个表面上也为0，满足法向磁场为零的边界条件。

3.2"电介质平板波导

这里考虑一个通信波段的平面光波导。在几何中建立一个长6"μm、高4"μm的矩形作为波导。建立一个长6"μm、高6"μm的矩形，与前一矩形共心。两个矩形之间厚度为1"μm，设为空气层。在材料中分别建立折射率为1和1.5的两种材料，波导内部折射率设为1.5，外部折射率设为1。同样采用“电磁波，频域”物理场。由于波导x方向也为无限长，需要添加一对“周期性边界条件”，选中x=-3和x=3两条边界，这样可以保证两侧电场分布相等。在设置中选择周期性类型为“连续性”。在“模式分析”中，求解波长为1"550"μm，有效折射率在1.5附近的10个解。

在求出结果中，只有有效折射率为1.489"8、1.488"6、1.459、1.454四个解为平面光波导的导波模式，分别为TE0、TM0、TE1、TM1。TE0的电场在波导中没有节点，而TE1的电场在波导中有一个节点。沿着y轴自y=-3至y=3做截线。二者的电场在波导内部分别为余弦和正弦分布，在波导外部均向远处呈幂指数衰减，在波导表面Ex连续。即电介质界面处，法向电位移矢量连续，法向电场强度不连续。

4"结语

本文利用有限元方法仿真了几种静态电磁场和电磁波的模型，在模型建立过程中结合边界条件设置和相应的方程讨论不同情形下不同电磁场的边界条件，根据仿真结果绘制电磁场空间分布图和分布曲线，直观展示边界上电磁场切向、法向的特点。以上模型在电磁场教学中具有典型性，又灵活多变，反应了根据电磁场在边界上的各方面特点，方便学生区理解、区分和记忆。本文主要讨论了有限元方法在电磁场边界条件教学中的应用，从本文中也可看出，有限元方法在电磁场及电流求解、模式分析等电磁场理论的多个方面都有强大的计算能力和直观展示性，可以在电磁场理论教学中发挥巨大的作用。此外，可以进一步引导学生自行设计模型来展示电磁场边界条件特点，增强教学的趣味性，提高学生的自主学习能力。

参考文献

[1]"GRAND"J，"ERIC"C"L"R."Practical"implementation"of"accurate"finite-element"calculations"for"electromagnetic"scattering"by"nanoparticles[J].Plasmonics，2020，15（1）：109-121.

[2]"任贺.静电/磁力探针表征介电及铁磁纳米薄膜有限元电磁场模拟[D].哈尔滨：哈尔滨理工大学，2021.

[3]"曾冲，向静，周登梅.基于三维有限元仿真技术的电磁场课程教学方法[J].现代信息科技，2021，5（3）：196-198.

[4]"高永潘，芦鹏飞，王川.有限元仿真辅助电磁场时域频域性质教学[J].物理与工程，2022，"32（4）：39-45.

[5]"崔小斌，季文杰."COMSOL"Multiphysics"软件在矩形波导课堂教学中的应用[J].实验室研究与探索，2021，40（11）：130-135.