基于相变技术的便携式储冷箱性能研究

2024-02-05张文宇赵长颖

制冷学报 2024年1期

张文宇赵长颖

(上海交通大学工程热物理研究所上海 200240)

随着人们生活水平的提高和科技的发展,人们对冷链运输的需求也正逐步增加。根据一项市场调研预计,2023年全球的冷链运输市场将达到3 000亿美元[1],然而目前冷链需求的快速发展却存在很多问题。一方面,近年来世界各地的食品冷链出现了很多温度失效的问题[2-3],该问题会使冷冻或保鲜食品出现微生物繁殖而造成食品变质,增加了食物中毒的风险[4]。在医药冷链领域,对储存温度极为苛刻的疫苗等药品会出现产品效力消失的问题,甚至可能出现因变质而导致的副作用[5]。因为温度失效的问题而导致每年约有35%的冷冻食品在物流运输过程中损耗[6]。另一方面,冷链的快速发展会造成能源不必要的浪费,传统冷藏车内大功率的压缩机造成额外的化石能源消耗并排放更多的温室气体,与节能降碳的理念背道而驰[7]。

为解决冷链运输中温度失效的问题,研究人员提出了很多相关的解决方案,例如建立冷链温度实时监测系统[8]、提高装载货品期间的温度标准[9]、研究冷链运输新技术[10]等。对于新技术的研究,使用相变材料作为冷链运输中冷能存储的介质是目前研究中广泛采用的方案。相变材料是在自身的相变温度附近发生物相转变时释放/吸收大量潜热的一种材料[11],它可以利用相变潜热储存夜间用电低峰时制造的冷量[12],并在后续冷链运输中将冷量释放至环境和货品中以达到延长储冷时间的效果。该模式使用了夜间电网低谷时所产生的电量,减轻了用电高峰季电网的负担,也减少了化石能源的消耗[13]。

目前相变材料已在电力调峰储能、建筑保温、废热回收、冷链运输[14-17]中被广泛研究。在冷链运输领域,现有冷链解决方案研究方向主要集中于冷藏集装箱和小型储冷箱及其储冷材料的研究[18-21]。对于储冷箱的研究,由于便携式储冷箱体积灵活、运输便捷,因此更适合在冷链末端开发应用[22]。Nie Binjian 等[23]设计了用于运输疫苗和新鲜食品的储存箱,储存温度范围为2～8 ℃,研究结果表明,使用相变材料可将便携箱维持2～8 ℃的时间延长至11.5 h,且使用复合相变材料后充冷效率和整体能量效率分别提升了6.09%和12.58%。Du Jianping等[24]对含有相变材料板的储冷箱进行了数值模拟研究,储存箱的使用温度区间同样为2～8 ℃,研究了相变材料的5种布局和2种保温材料对箱体的有效保冷时间的影响。研究发现,相变材料的不同布局对箱体的保冷时间影响显著,不同种PCM对保冷时间也有影响,但并未分析具体的原因。Xu Xiaofeng等[25]研究了一种基于相变材料和真空板的多温区储冷运输单元,其中3个存储温度区间分别为常温(20 ℃)、7～10 ℃和-3～-1 ℃,最终保温箱的中温区和低温区可以分别在7～9 ℃和-2～0 ℃保持约13 h。S. Burgess等[26]在Du Jianping等[24]研究的基础上,探讨了存在负载情况下相变材料在箱体内的布局。认为最佳布局方式为PCM在箱体的顶部、底部和长侧面各分布25%。在储冷时间方面,具有高潜热的PCM表现更优且较低的PCM熔化温度会导致较高的放电效率和较低的温度不均匀性。与相变材料配合延长整体保冷时间的保温材料通常为真空板,作为新型保温材料,真空板因结构特殊具有超低的导热系数[0.008 W/(m·K)],可以应用于不同的保温场景[27-28]。在上述研究中已有涉及真空板作为保温材料对储冷箱性能改进[24-25]的探索,并且研究表明真空板的存在可以大幅延长储冷箱的保温时间。

分析上述研究发现,现有研究整体聚集于食品保鲜即2～8 ℃的温度区间内[23-24,26],而涉及冷冻区间(<-18 ℃)的保冷研究则相对较少。在对真空板的研究中,没有分析真空板在箱内的具体布局以及真空板厚度参数对整体保温效果的影响,缺乏对真空板作用效果的系统分析。在对PCM的布局进行分析时,S. Burgess和Du Jianping均在恒定PCM质量情况下,对不同位置的相变材料平均分配或固定分配以分析不同相变材料布局的性能,但由于每个位置能够放置的相变材料质量会因尺寸等关系而随之变化,因此该方法并不能分析箱内不同位置的PCM(顶部、底部和侧面)对储冷性能的单独贡献情况。

为解决上述问题,本文设计了一种相变材料和真空板耦合的适用于存储冷冻产品的冷能储存箱,对储冷箱性能进行模拟分析,并对结果进行实验验证。本文通过有效保冷时间、PCM的冷量功耗和单板保冷系数等参数对储冷箱进行了优化设计,并对不同的环境温度、不同相变温度的PCM和真空板空间位置与厚度参数对冷藏箱性能的影响进行了分析。在每个位置可能承载的最大PCM的基础上,对箱内不同位置的相变材料对储冷性能的贡献程度进行了量化。通过上述研究可以对应用于冷冻货品末端运输的储冷箱设计及相变材料和真空板在储冷箱内的使用起到一定的指导作用。

1 实验与数值模型

1.1 实验材料

实验设计的储冷箱如图1所示,其外部尺寸为260 mm×350 mm×445 mm,内部容积为27.62 L。箱体主体使用外部聚乙烯(PP)材料(1 mm)保护、内部聚氨酯(PU)材料(19 mm)保温;PCM装填在由聚乙烯材料制成的板壳内而组成PCM板,且PCM板通过内附的方式贴附在箱内的各个面上,板的厚度为20 mm。根据储冷箱的实际储冷温度,选择十一烷(相变温度为-25.75 ℃,上海迈瑞尔化学试剂有限公司)作为相变材料,使用相变材料的总体积为6.19 L。使用置于箱体底部中心的冰块(200 mm×80 mm×160 mm)作为内容物,该冰块在箱内有效空间中体积占比为15.15%,处于实际应用工况范围之内,且较低的体积占比可以更好的观察内部温度场的变化。为了解在储冷过程中箱体内部温度分布状况,使用误差为±0.4%的T型热电偶收集箱内温度,共设置9个温度采集点,其中6个分布于PCM板内表面各面中心处、2个分别设置在冰块体积中心处和上表面中心处,1个设置在储冷箱外部以采集环境温度。使用盘古KT612R无纸记录仪记录实验过程中温度随时间的变化。

图1 储冷箱

1.2 实验方法

实验开始前,将实验所需的冰块通过冰箱降温至-20 ℃并保持恒定,同时使用冰箱将相变材料板的温度控制在-30.7 ℃。将储冷箱所处的室内温度控制在约25 ℃,当冰块和相变材料温度均达到相应的设定温度后,将其同时按顺序放入储冷箱中,并将储冷箱的顶部盖合。此时使用热电偶采集相应温度测点的温度,记录储冷箱内温度场和环境温度的变化,直至冰块中心温度高于-18 ℃为止。

1.3 物理模型

通过SolidWorks建立仿真所需几何模型,模型包含PP+PU聚氨酯箱体、相变材料板、真空板(vacuum insulation panel,VIP)和所存储的冰块,具体尺寸与实验设计的储冷箱相同,如图2所示。使用COMSOL Multiphysics软件对建立的模型进行储冷箱内部温度场的瞬态分析,储冷箱外部模拟空气的自然对流,相变材料板内部考虑材料自然对流,储冷箱内仅考虑热传导。由于储冷箱在热耗散过程中主要为箱体表面的自然对流和内部的热传导,因此忽略储冷箱在开合过程中的冷量损耗,忽略材料和箱体材料之间的热辐射。为了简化计算,忽略存储相变材料和冰所使用的容器厚度,假设不同组分之间无间隙。此外,假设空气为理想气体,其余材料均假定各向同性。

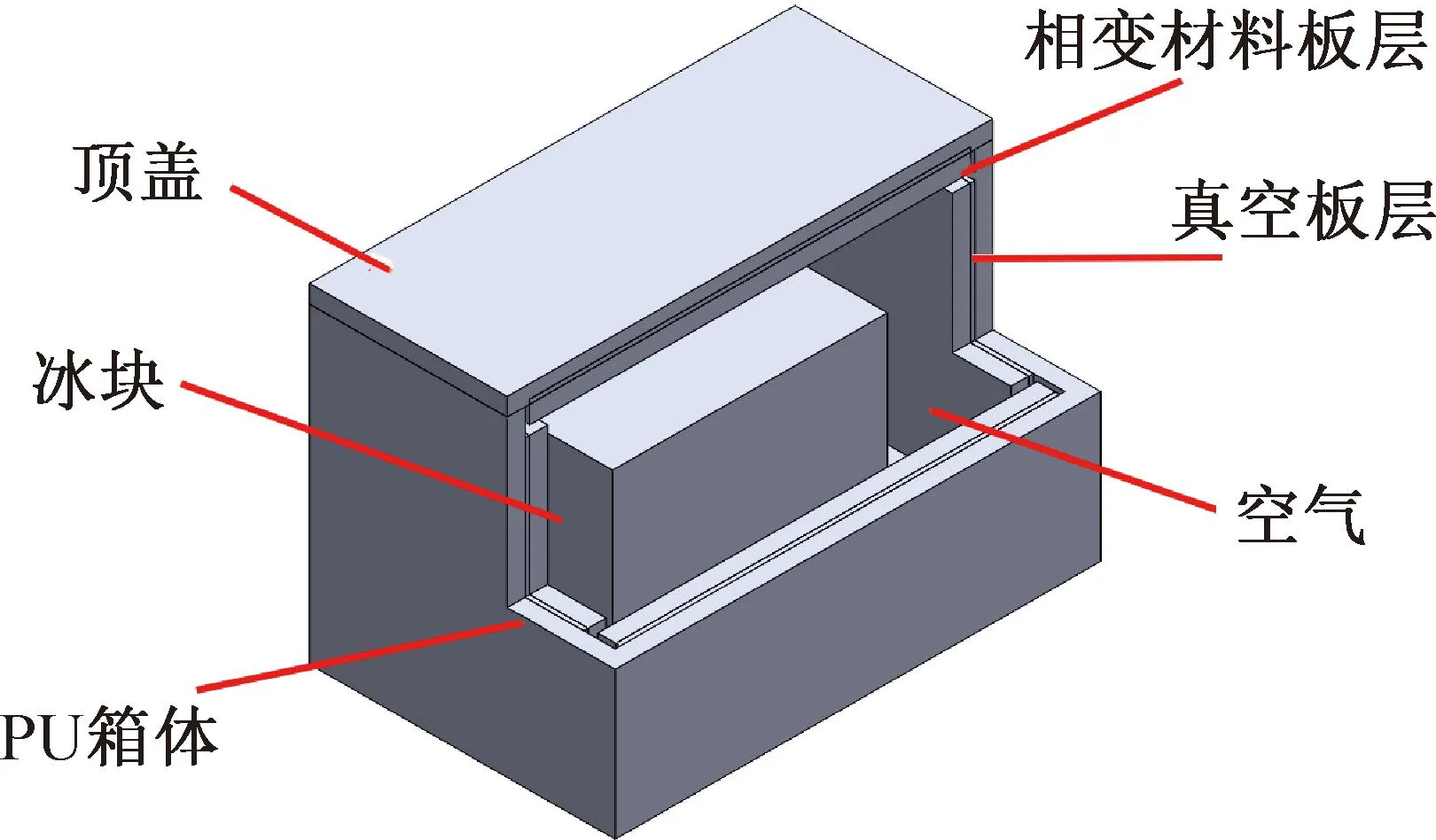
图2 储冷箱几何模型(仿真)

1.4 数学模型

根据建立的几何模型推导发现,本模型在冷量耗散过程中主要方式为固液之间的热传导、箱体外部空气的自然对流和环境对箱体的热辐射。因此,固体和液体热传导的瞬态方程为:

(1)

(2)

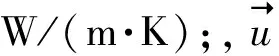
在相变材料熔化时,会因重力作用而在板内形成对流,其质量守恒和动量守恒方程为:

(3)

(4)

(5)

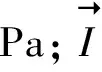
ρ=ρsolid

(6)

(7)

(8)

k=θ1k1+θ2k2

(9)

θ1+θ2=1

(10)

式中:Lm为材料在相变过程中的相变潜热,J/kg;θ1、θ2为相变前后的相分数;cp,1、cp,2分别为相变前、后的比定压热容,J/(kg·K);k1、k2分别为相变前、后材料的导热系数,W/(m·K);ωm为相变后液体状态的质量分数。在储冷箱外部,为简化模型设置,6个面均简化为在环境温度下空气的自然对流,其中侧面遵循垂直壁自然对流模型,其传热方程和对流传热表面传热系数的表达式为:

(11)

q0=h(Text-T)

(12)

(13)

式中:q0为边界上的总热量,W/m2;h为对流传热表面传热系数,W/(m2·K);Text为外部环境温度,K;L为箱体壁表面的特征长度,m,此处为储冷箱侧壁的高度;RaL为瑞利数,其表达式为:

(14)

式中:β为流体的体积膨胀系数;ν为流体运动粘度,m2/s;α为热扩散系数,m2/s。

1.5 初始参数设定

将物理模型导入仿真软件后,为能够更全面的计算和得到更精确的结果,需要对模型的初始值和边界条件进行设定:

1)在标准参照模型中,PCM的初始温度设置为-30.75 ℃,比相变温度低5 ℃;

2)环境温度设置为25 ℃,以符合正常的存储条件;

3)VIP的厚度设置为5 mm,导热系数为0.008 W/(m·K)[29];

4)VIP和冰块的起始温度设置为-20 ℃;

5)箱体外部的表面发射率设置为0.9,以衡量环境对箱体外表面的热辐射;

6)使用软件中自带的网格工具划分网格,网格类型为自由四面体网格。网格包括221 002个单元,以网格偏度为基准的平均单元质量为0.657 8;

7)使用具有0.1 h初始步长和0.001容差的瞬态求解器进行模拟计算;

8)当箱体中心冰块的平均温度达到-18 ℃时,停止计算并收集数据。

1.6 性能参数设定

为了能够对不同变量控制下的算例之间储冷性能进行对比,本文规定-18 ℃为储冷箱内冰块的临界存储温度,当箱内存储温度高于临界存储温度时储冷箱的储冷性能失效;箱内冰块平均温度到达临界存储温度所经历的时间称为有效保冷时间,记作tecp(h);PCM完全熔化所需要的时间称为熔化时间,记作tmelt(h);在储冷箱内因为PCM的存在冰块所降至的最低温度称为Tmin(℃)。

同时为衡量PCM对冰块释放冷量的均匀性,本文引入均匀系数的概念,计算式为:

ε=tmelt/tecp

(15)

该系数表示PCM完全熔化时间所占有效保冷时间的比例。均匀系数可以在一定程度上表示该PCM在储冷箱内的适宜程度,系数太小则说明PCM熔化过快,相变潜热的利用率低;同时若该系数越大,PCM完全熔化所用的时间占总保冷过程的时间的比例越大,其冷量可以在箱内更均匀的释放,达到更优的储冷效果。

从能量利用角度分析,达到相同的tecp所使用的PCM冷量越少表示冷量利用的比例越高,同一时间内冷量耗散小,可以进一步降低储冷箱在储冷过程中的碳排放。为了对比不同参数变量影响下PCM冷量使用的高低,本文定义冷量功耗的概念,表述为在有效保冷时间内PCM所释放的冷量与释放时间的比值:

(16)

式中:mi为不同位置PCM的质量,kg;Ti和θi分别为不同位置PCM在Tmin时的温度(℃)和相变程度;Tinit为PCM的初始温度,℃。在相同的有效保冷时间内,冷量功耗越低代表消耗的冷量越少,功耗越高代表能源浪费越严重。因此,在其他参数相同的条件下,对PCM的选择应同时考虑冷量功耗高低所带来的影响。

2 结果与分析

2.1 结果验证

2.1.1 网格无关性验证

在对模型进行计算的同时,网格单元尺寸的大小可能会影响计算的精确度。为了对模型的网格独立性进行验证,本文使用相同方式生成了常规、细化和较细化3个级别的自由四面体网格,其单元数依次为100 811、221 002和620 601。对3种单元数的模型进行计算,对比其内部冰块温度随时间的变化,结果如图3所示。由图3可知网格数量越多冰块温度变化越缓慢,但当规格为细化和较细化时,其整体变化相差较小,其在达到-18 ℃所使用的时间仅相差0.85%。因此,本文认为网格规格为细化和较细化两者之间存在无关性,为了节省计算资源,选择单元数为221 002的细化网格进行后续的模拟计算。

图3 不同规格网格下冰块温度的变化

2.1.2 实验验证

为验证仿真结果的准确性,建立了与上述实验模型相同的物理模型,便于对比实验结果和仿真结果。为保证实验与仿真算例的一致性,仿真模型的环境参数使用实验过程中采集到的温度数据。经过实验和模拟计算,对比了实验和仿真算例在冰块中心和底部PCM板中心这两个位置的温度变化,对比结果如图4所示。由图4可知,在所测位置实验与模拟算例的温度趋势基本一致,并且在5 h时,冰块中心处的温度差仅为0.42 ℃。在有效保冷时间方面,实验过程的有效保冷时间为7.4 h,仿真情况下有效保冷时间则为7.72 h,两者相差0.32 h,差距为4.32%。出现差距的原因可能来自于实验箱体各部件之间存在的微小缝隙,导致一部分冷量从缝隙中泄漏,进而使实验所得温度有所偏高,使有效保冷时间tecp缩短。

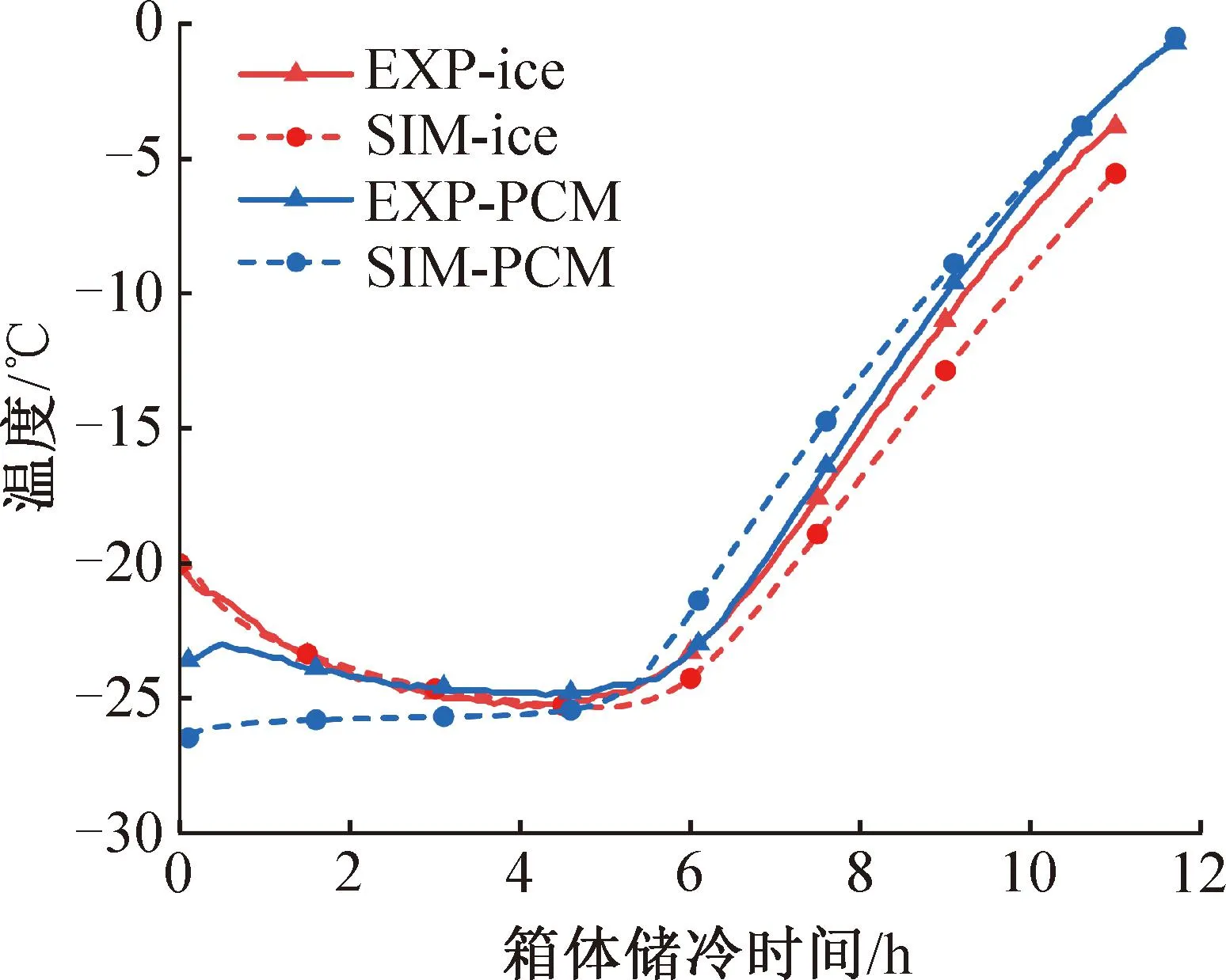
图4 数值模拟与实验结果对比

2.2 不同环境温度的影响

在储冷箱的实际使用过程中,外界环境温度的高低变化是影响储冷箱保冷性能的关键因素。对照算例(环境温度为25 ℃,相变材料为十一烷,真空板厚度为5 mm)中的环境温度分别设定为20、25、30、35 ℃,并分别进行计算,得到不同环境温度下储冷箱内冰块平均温度随时间的变化,如图5所示,记环境温度为Tamb,分析储冷箱工作环境温度的高低对储冷箱性能的影响。由图5(a)可知,在相同的时间条件下,储冷箱所处的环境温度越高,其内部冰块的平均温度越低,说明环境温度的变化对箱内储冷过程的温度场影响显著。分析了环境温度和冰块初始存储温度的温差与有效保冷时间之间的关系,如图5(b)所示。PCM的熔化时间随着冰块初始温度与外界温差的扩大而不断减小。与此同时,当温差为40～55 ℃时,其内部有效保冷时间依次为29.27、25.78、23.22、21.55 h,由此可知,温差越大,有效保冷时间越短。温差每升高5 ℃时,有效保冷时间最大缩短了3.49 h;并且以环境温度25 ℃为基准,温差上升22.2%时,有效保冷时间降低了4.23 h,降幅为16.4%。该数据表明,环境温差较大时会显著降低储冷箱的有效保冷时间,在实际应用中应避免储冷箱所处的环境温度过高。

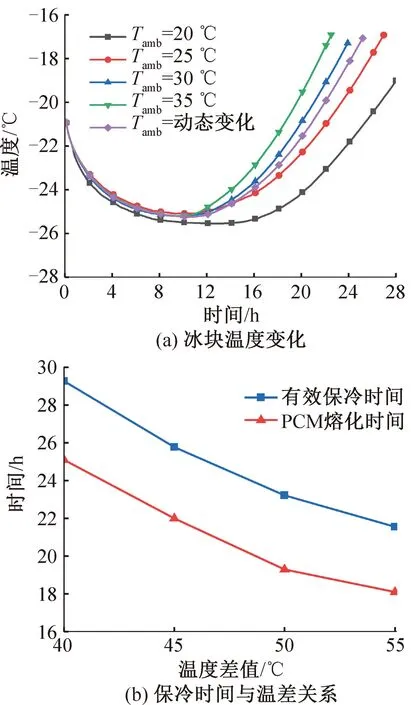
图5 不同环境温度下储冷箱储冷性能变化

为了探究储冷箱在实际使用过程中内部温度的变化,将固定的环境温度替换为一天内实时变化的温度,导入Comsol中进行计算,得到更符合实际的内部温度场随环境温度的变化。选取上海测温站夏季某天历史温度记录作为实时变化的环境温度数据,将该环境温度记为Tvar,虽然此温度在一天内波动较大,但由图5(a)可知在储冷箱内部PCM温度和所存储冰块的平均温度变化曲线表现出较好的平稳性,并未产生明显的波动,说明储冷箱对外部温度波动具有很好的抵抗性。产生该结果的原因主要是箱体隔热材料自身的低热阻使外部温度变化时通过箱体壁的热流量变化较小。Tvar的平均温度为28.35 ℃,且其相变材料熔化速度和内部存储冰块平均温度的变化曲线均在Tamb=25℃和Tamb=30℃的曲线之间,符合其平均温度在25～30 ℃的预期。说明当外界环境温度波动时,储冷箱可以依靠PCM的温度缓冲能力中和环境温度变化带来的影响。并且面对实际使用过程中不断变化的环境温度,在分析其对储冷箱有效保冷时间的影响时,可以取环境温度平均值对储冷箱保冷时间进行初步估计。

2.3 真空板的保冷作用

2.3.1 真空板厚度

真空板(VIP)作为保温材料有着比PU材料更低的导热系数,保冷性能更优。为探究VIP在储冷箱中的使用效果,以算例中VIP厚度作为变量,其他条件不变,研究VIP厚度对保冷时间的影响。VIP厚度分别定为0(无真空板)、2.5、5.0、7.5 mm。分析5 h时不同厚度算例的温度云图(图6)可知,当VIP存在时,箱体内部温度明显降低且温度均匀性优于无VIP时的算例,且这一特征随着VIP厚度的增大而更加显著。因为VIP厚度增加可以有效降低箱体壁的热阻,减缓箱体内部冷量的散失,从而使箱体内部温度一致性提高。该结果表明,VIP可以有效隔绝外部热量的侵蚀,使箱体内部在一定时间内维持较低的温度。

为分析不同VIP厚度下箱体储冷性能的差异,以VIP厚度5.0 mm为基准,分析VIP厚度分别增加/减少50%时的保温效果。分析不同厚度下PCM完全熔化时间和箱体的有效保冷时间,结果如图7所示。VIP的存在使相变材料熔化速度明显放缓,相变材料完全熔化所需时间大幅延长。VIP从无到有可以使相变材料的熔化时间最大延长14.6 h,延长了136.4%;同时使有效保冷时间延长19.43 h,增幅为197.7%。分析tecp和VIP厚度的关系时,可以发现储冷箱的tecp随VIP厚度的线性增长而不断增加,当VIP厚度由d增加50%变为1.5d时,可以使有效保冷时间延长13.3%。其余算例的有效保冷时间、增量以及增幅的具体数值如表1所示,分析数据可知,tecp随VIP厚度的增长而不断增加,但增幅明显降低。例如在VIP厚度从0增至0.5d和从d增至1.5d时增幅相同,但由此产生的有效保冷时间变化后者仅为前者的31.1%。该结果可由通过壁面的热流密度与厚度之间的关系得到验证,仅考虑导热时从箱体冰块至外部环境的导热公式为:

(17)

图7 VIP厚度对有效保冷时间和PCM熔化时间的影响

式中:r0为除真空板热阻之外的总热阻,K·m2/W。

由式(17)可知,热流密度q与真空板厚度d之间为反比例关系,当d不断增加时,q的减少并非线性,而q的大小决定了有效保冷时间的长短,因此可以推断d的增加对保冷效果的提升存在一定的边际效应。分析不同厚度VIP的算例中均匀系数ε和冷量功耗Pcold(图8)发现,当箱体内存在VIP时PCM的ε会有较大的提高;且冷量功耗随着VIP厚度的增加而不断下降,当VIP厚度为1.5d时冷量功耗仅为无VIP的34.57%,再一次验证了VIP在储冷箱内的重要性。

图8 VIP厚度改变时均匀系数和冷量功耗的对比

2.3.2 真空板位置

在标准对照算例中,PU材料、相变材料和真空板从外到内布置形成了储冷箱保冷的复合结构。但3种材料因导热系数等性质的不同,其布置顺序可能也会影响储冷箱的保冷效果,为分析该布置顺序对保冷效果的影响,对照算例的3种材料进行重新排序并计算分析。由于PU材料需要作为外壳材料以保证储冷箱足够的物理强度,因此本文分析内部相变材料和真空板的相对位置对储冷效果的影响,结果如图9所示。在算例1中,PCM层位于VIP层的外侧;在算例2中,则位于VIP层的内侧。对于这两种不同算例,其中PCM层及VIP层厚度和热物理性质与参照算例中相同。由图9可知,当真空板在外部布置时,相变材料的熔化速度明显放缓,最终tmelt比其在内部布置延长了9.5 h,且有效保冷时间从16.71 h增至25.78 h,延长了54.3%。在有效保冷时间内,冰块的平均储存温度也不尽相同,VIP在外侧的布置可以使冰块平均温度Tave由-20.88 ℃降至-23.26 ℃,降低了2.38 ℃。这是因为当VIP布置在PCM外侧时,VIP层可以在很大程度上阻挡向内的热量,使PCM有足够长的时间使用其相变潜热进行保冷。在PCM相变期间,由于PCM的等温特性,内部温差减少,从而降低了内部的传热速率和通过箱体内壁的热通量。该原因可以从两种布置方式下ε和Pcold的差异中得到佐证,通过计算得出算例2的ε和Pcold分别为0.64和25.30 W,均优于算例1的0.53和39.62 W,说明算例2中PCM的相变潜热得到了更长时间和更有效的利用。因此VIP在外侧可以将PCM冷量更均匀的传递给冰块同时降低冷量功耗,进而延长有效保冷时间。所以本文认为在其余参数相同的情况下,真空板在外侧、相变材料在内部的布置方式能够减少冷量损失,增强储冷箱性能。

图9 相变材料和真空板排列顺序对温度场的影响

2.4 不同种相变材料的影响

相变材料作为储冷箱中最为重要的储冷保温材料之一,不同种类相变材料的选择直接决定了其保冷效果的差异。为研究不同热物理性质的相变材料对储冷箱保温效果的影响,并根据实际的保冷温度需要,选择2-辛酮、正十一烷、正癸烷和2-辛酮与正癸烷混合物(50:50质量百分比)4种不同的有机相变材料对其储冷效果进行研究,分别记为PCM1～4,具体物理性质如表2所示,模型中其余参数均与参照算例中相同。

表2 PCM的热物理性质[30]

由表2可知,因其同属于有机相变材料中的烃类和酮类,本文采用的4种相变材料具有相似的导热系数和密度,同时这4种材料在相变温度和相变潜热方面则存在较大差异,其中PCM1的相变温度最低,PCM3的相变温度最高且与冰块的初始存储温度仅相差1.55 ℃。图10(a)～(b)为4种相变材料的相变速度和相变材料温度的变化,可以看出,PCM3的相变速度最慢且在相变时温度变化程度小的平台期持续时间很长;同时在相同时间内PCM2的相变进程最快,这也导致其温度在短时间内迅速上升。PCM的相变速度和相变温度的区别直接导致了有效保冷时间上的差异,图10 (c)为使用4种PCM的箱体内部冰块的平均温度变化,分析可知,虽然PCM3的冰块最低温度明显高于其他PCM,但其最低温度最为稳定,且PCM3具有最长的有效保冷时间33.94 h。当选用PCM1时冰块温度最低达到-28.64 ℃,但冰块温度并未保持且随着时间的推移迅速升高,最终有效保冷时间为31.29 h。对于PCM相变潜热对保冷时长的影响,通过对比PCM2和PCM4发现二者具有相似的相变温度和初始温度,但相变潜热的不同导致有效保冷时间不同,在箱内装载PCM4时比PCM2的有效保冷时间长6.16 h,延长了23.89%。在PCM的其他热物理性质基本相同的情况下,出现该现象是因为PCM的相变潜热可以在PCM相变过程中持续为箱内提供冷量,减缓箱内温度升高致使PCM的潜热越大,对箱内传递冷量越多,即提供更长的保冷时间。

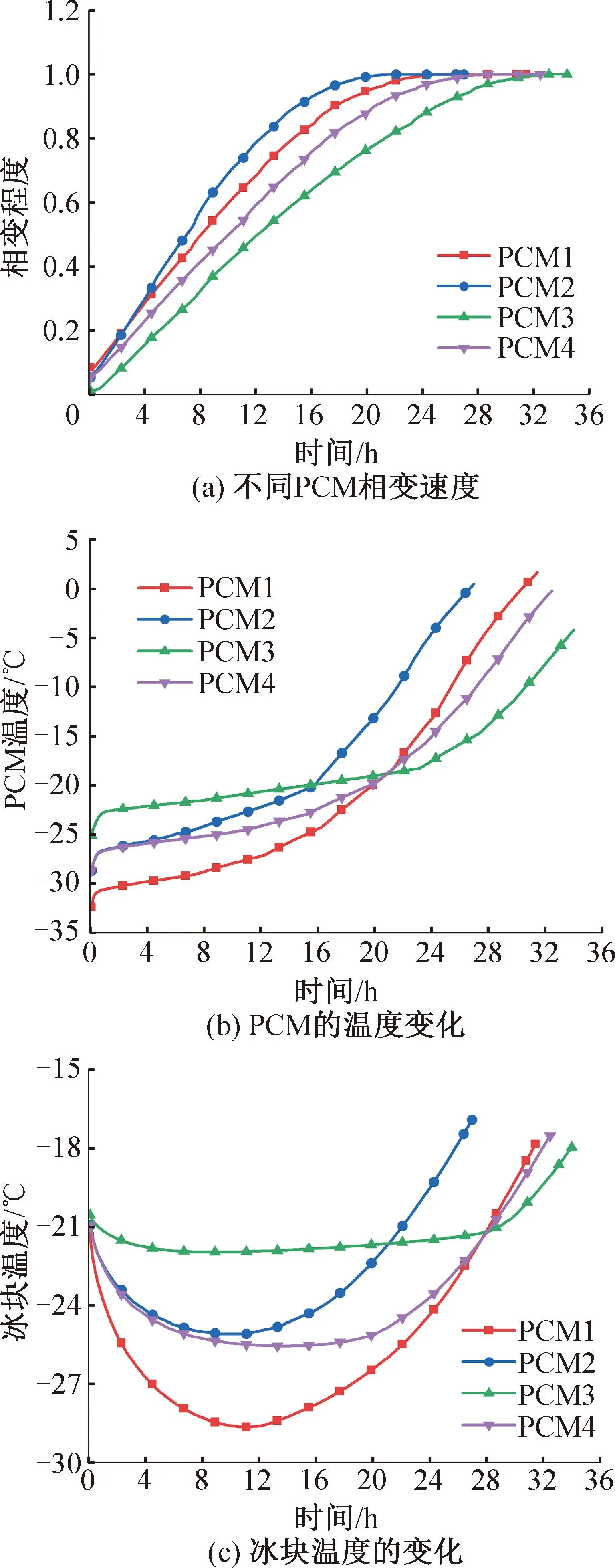
图10 不同相变材料相变速度及箱内温度变化

分析PCM1、PCM3和PCM4在箱内的保冷过程,3种PCM具有基本一致的相变潜热,相变温度和相变材料的初始温度不同,导致不同相变材料初始温度与冰块初始温度之间的温差存在差异:PCM3的相变温度与冰块初始存储温度的温差最小,PCM1的温差最大。由图10可知,对比3种材料的相变速度和温度以及箱内冰块温度变化情况可知:PCM3的性能表现最优,具有最长的有效保冷时间;而相变温度最低的PCM1反而因为后期温升速度过快而表现最差。分析产生该现象的原因可能为PCM1因为较大的温差而与外界环境在箱体壁上产生较大的热流量,较大的热流量又导致PCM熔化速度的变快,造成初期相变潜热的不合理释放,进而缩短了整体的保冷时间。装载不同PCM的储冷箱性能分析如图11所示,通过分析三者的均匀性系数验证了该结论,PCM1的均匀系数为0.62,在3种材料中最低,而PCM3的均匀系数达到0.88,在3种材料中最高。这表明虽然PCM3的相变温度与初始存储温度温差最小,但其相变潜热向箱内释放最均匀,达到最佳的有效保冷时间。进一步分析了PCM1和PCM3算例中通过箱体底部的热流量差异,结果如图12所示。由图12可知,在开始的一段时间内,由于PCM1的初始温度较低且外界环境的温差更大,因此热流量更大,相变速度也加快。随着相变过程的进行,固态的相变材料逐步转变为液态,导热系数随之下降,PCM3因为更快的相变速度,导热系数下降更快,通过壁面的热流量也下降更快,因此出现了PCM1中的热流量在19 h后低于PCM3的结果。PCM1因为相变温度和冰块存储温度的温差很小,初始相变速度更慢,允许其在相变期间释放的冷量均匀的转移至冰块中,从而壁面热流量释放更均衡,延长了储冷箱的有效保冷时间。通过上述分析,推断PCM的相变温度与冰块的起始存储温度之间的温差对其均匀系数有一定影响,具体为在其他热物理性质相同的情况下两者的温差越大,冷量释放的均匀性越低,均匀系数的数值越低,进而导致保冷性能下降。

图11 装载不同PCM的储冷箱性能分析

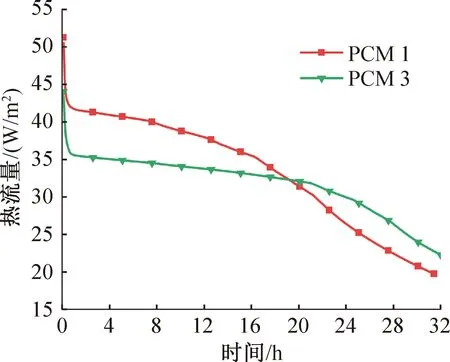
图12 PCM1和PCM3的箱底热流量变化

本文从储冷过程中冷量损耗的角度出发,分析4种PCM在能源消耗方面的差异,寻找在整个储冷周期内能源使用最合理的材料。在箱体储冷过程中,PCM的冷量主要有两个去向,一方面通过箱体壁向环境释放,另一方面向箱内冰块中释放。因此影响冷量功耗的主要因素为箱体壁热阻大小和PCM与冰块之间的温差,而在本组算例中除PCM的种类不同外并无其他差异,因此不同PCM的冷量功耗差距并不显著。4种PCM的冷量功耗差异关系如图11所示,冷量功耗最低的为PCM3,仅为24.22 W;最高的为PCM1,达到27.36 W。更低的冷量功耗可以降低因PCM蓄冷所产生的电力成本和碳排放。可知在储冷箱使用PCM3作为相变材料时,消耗的能源更少,更有利于行业的节能减碳。

本节主要研究不同PCM算例的有效保冷时间、均匀系数和冷量功耗之间的差异,综合考虑上述3种性能指标,将不同PCM的性能指标数值进行线性函数归一化分析,选取每种指标中最优值为1,结果如表3所示。PCM3为本研究中最适合存储温度为-20 ℃的PCM种类,归一化性能总分为3.00。因此PCM3在本研究所考虑的3种性能指标中均为最优,其有效保冷时间最长,均匀系数最佳,说明PCM的相变潜热利用最充分。在其余3种PCM中,PCM2在性能排行中表现最差,归一化性能分仅为2.44。

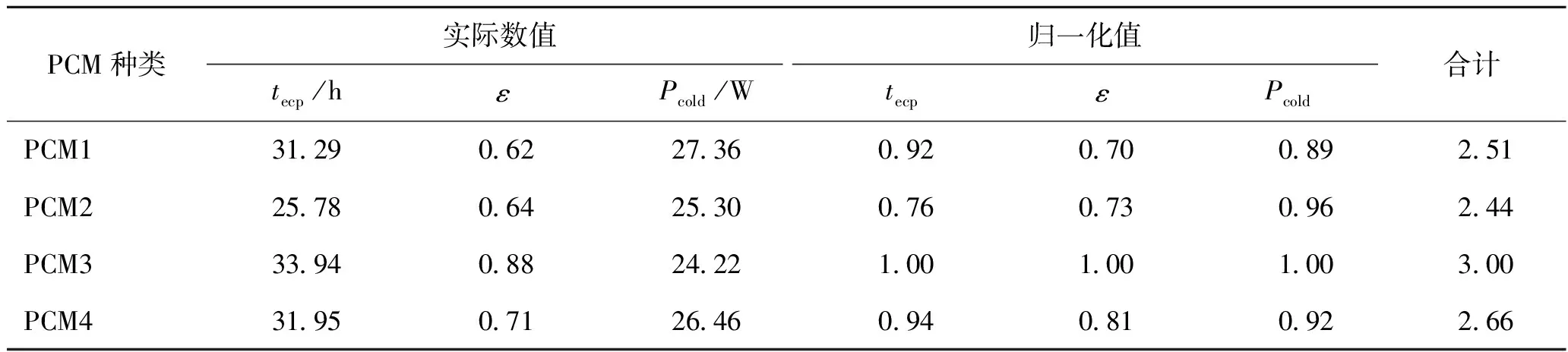
表3 不同种PCM的性能系数对比

本研究中分析了PCM的相变潜热、相变温度和冰块初始温度的差值等性质对箱体保冷时间的影响。然而PCM的其他一些性质并未被考虑,例如导热系数、密度和比热容等热物理性质,其数值差异同样可能对储冷性能产生影响。因此本文将标准算例中正十一烷材料的导热系数、密度及比定压热容的数值通过控制变量的方法分别降低50%和增加50%后进行模拟计算,以分析它们对储冷箱有效保冷时间的影响。不同工况下有效保冷时间及差异如图13所示,由图可知,PCM的密度变化对有效保冷时间的影响最大,其次是导热系数和比定压热容。其中密度的增加会使PCM的有效保冷时间大幅延长,增强箱体的保冷性能;而PCM的导热系数和比定压热容的增加则会减少储冷箱的有效保冷时间。分析导致该结果的原因应为本模型中PCM为控制体积,更大的密度意味着更多质量的PCM在其中发挥作用,有更多的相变潜热可以利用,因此对箱体的保冷时间影响最大。导热系数和比定压热容的变化对保冷时间的影响较为温和,单独减少50%的导热系数和比定压热容仅分别增加了0.79 h和0.11 h有效保冷时间。但值得一提的是,当PCM的密度越大时,意味着整个箱体的质量越大,会增加箱体在运输中的成本和降低使用体验。

图13 相变材料的热物理性质对有效保冷时间的影响

2.5 不同位置相变材料的保冷能力

在前文所述的参照模型中,箱体内相变材料板在6个面上均有附着,但不同位置的相变材料板因与储存介质的空间位置关系和自身质量的不同,其保冷效果会存在差异。为研究不同位置相变材料板对整体保冷效果的影响,在其他条件保持不变的情况下,根据箱体的对称性分别只保留参照模型中单侧短边、单侧长边、底部和顶部的相变材料板,记为位置1～4,如图14所示,对4个位置的PCM板分别单独存在时的仿真模型进行计算,研究其内部温度分布情况和不同位置板的贡献度。为量化不同位置PCM板的贡献程度,本文定义单板保冷系数的概念,记为ηi,计算如下:

图14 不同位置的PCM示意图

ηi=tecp,单板/tecp

(18)

式中:tecp,单板为只有单相变材料板存在时的有效保冷时间,h;tecp为所有位置相变材料均存在时参照算例的有效保冷时间,h。单板保冷系数可以在一定程度内有效量化不同位置的相变材料对箱体保冷性能的贡献大小,其数值越大,说明PCM板单独存在时的保冷时间越长,占总保冷时间的比例即越大,对箱内总保冷性能的贡献越大。

不同位置PCM板单独存在时的相变速度及冰块温度变化如图15所示。由图15(a)不同位置PCM的相变速度可知,当PCM单独存在时,相变速度均有所加快,位置3算例的完全相变时间仅为11.2 h,但由图15(b)箱内冰块温度可知,位置3处的PCM具有最佳的保冷效果,其有效保冷时间tecp达到11.7 h,比时间最短的位置1多了434.2%。5 h时箱体横截面不同位置PCM算例的温度云图如图16所示。由图16可知,当相变材料板在底部时,相变材料与冰块的温度均匀性最好且趋于一致。出现上述结果的原因为底部相变材料板因与冰块直接接触,相变材料的冷量更多的通过热传导转移至冰块中,加快了PCM的相变速度,使同一时间时冰块的温度较其他位置更低,达到更长的保冷时间。其余3个位置的算例虽然PCM的相变速度很慢,但因未与冰块接触,PCM的冷量只能通过与冰块之间的空气进行热传导而将冷量传导入冰块中。而该过程的冷量远小于冰块散失的冷量,因此如图15(b)所示,冰块的温度从一开始就出现了上升,且该处PCM的冷量大多散失于环境中。

图15 不同位置PCM板单独存在时的相变速度及冰块温度变化

图16 5 h时箱体横截面不同位置PCM算例的温度云图

对不同位置PCM的单板系数计算结果如表4所示。当相变材料在底部单独存在时其单板系数最大,达到0.454;其余3个位置的单板系数均低于0.1,数值最低的是单侧短边的单板系数,仅为0.085。根据单板系数的定义可以得出,在储冷过程中,对箱体保冷贡献最大的为箱体底部的相变材料,贡献最小的为侧面短边的相变材料。虽然该系数可能会因为所存储货品的位置不同而发生变化,但通过本研究仍可以认为与货品直接接触的PCM板对其保冷性能的贡献将会最大,PCM将冷量释放至冰块的过程和比例直接影响了有效保冷时间的长短。同时,通过计算可得6个面总的单板系数之和为0.907,并未达到最大值1,即当不同位置的PCM均存在时,各位置PCM对箱体的保冷存在协同作用。