求解量子控制问题的一种直接离散方法

梅自艳,王汉权

(1.云南财经大学 统计与数学学院,云南 昆明 650221;2.云南大学滇池学院,云南 昆明 650504)

量子力学中的薛定谔方程描述了量子系统的运动.随着量子信息技术和量子计算的不断发展,为满足对复杂量子系统进行操纵和控制的要求,这就需要从控制论的角度对微观量子系统的行为进行建模、分析和主动控制,于是量子控制论应运而生.量子控制的研究始于20世纪70年代末,是量子力学和控制理论交叉的结果,目标是建立对量子系统进行控制的普遍理论和方法.随着量子力学的发展,量子控制模型也相应发生改变[1].

Bennett 等先提出一种新的通信和计算量子理论,其中传输或处理的不是经典信息,而是量子态的任意叠加[2].随后,Doherty等指出鲁棒控制理论中的分析和综合技术的应用将发挥重要作用,且在量子计算等新兴量子技术的发展中发挥着重要作用[3].针对量子通信和量子计算等量子信息学的发展趋势,陈宗海等对量子控制系统全面地介绍了量子控制实验研究现状并进行了相关研究展望,并阐述了一些新的研究思路[4-5].对于在开环量子控制领域,Dong等综述了量子系统可控性的概念,提出了几种控制设计策略,包括最优控制、基于 Lyapunov方法、变结构控制和量子非相干控制;在闭环量子控制领域,该文回顾了闭环学习控制以及与量子反馈控制相关的几个重要问题,包括量子滤波、反馈稳定、线性二次高斯控制和鲁棒量子控制[6].本文主要考虑量子控制问题中的一种特殊但又相对重要的情况：如何最优地把激发态解操控至基态解.针对此问题,文中提出一种直接方法：通过离散方法,把量子控制泛函极小值约束问题转化为普通的优化问题进行求解.

前期,对量子最优控制的问题已经开展了较多的研究.Rabitz 等对量子系统最优控制问题解的存在性、数学近似处理方法和最优控制的应用等进行了详细的论述[7].近年来,D’Alessandro等在量子最优控制方面做了大量工作,并通过李群分解的分析方法给出了一些控制场能量最优的量子控制结果[8].Wu等总结了时间最优时量子控制的一般特征,并给出了一些特殊情况下的最优极值的结构[9].Petersson等研究了在封闭量子系统中实现逻辑门的最优控制问题[10].Boscain等综述了各种量子控制问题,并描述了适合于最优控制的数学公式,详细介绍了不同低维量子系统的最优解,说明了数学工具是在实际中如何应用的[11].薛拾贝等对量子系统时间最优控制问题进行了描述,并提出一类同伦算法[12].Dong 概述了量子系统最优控制的基于梯度的学习、量子系统学习控制的进化计算、基于学习的量子鲁棒控制和量子控制的强化学习等方面[13].近年来提出许多求解约束条件为Gross-Pitaevskii 方程(GPE)的数值方法,如有限元法[14]、有限差分法[15]、无网格法[16]和时间分裂伪谱法[17]等.对于GPE方程的离散方法,相关学者也介绍了一些相应的方法,比如Chebyshev谱方法[18],有限差分法[19].通过这些方法把方程进行离散,能更好的进行数值求解.对于求解控制问题所需的优化方法,常见的有最速下降法、牛顿法、拟牛顿法、共轭梯度法等等[20].

针对如何最优地把激发态解操控至基态解这一特殊量子控制问题,本文提出一种直接离散方法：先把连续性泛函及约束条件离散,使原控制问题变为普通的优化问题,然后采用普通的优化方法求解.重点讨论如何对量子控制问题进行直接离散,如何把量子最优控制问题转化为普通的优化问题,探讨该数值方法的特点.本文的结构安排如下：第2节中将对量子控制方程的模型及解满足的Euler-Lagrange(EL) 方程进行介绍及求解.第3节主要对连续性泛函及约束条件的直接离散方法进行详细的推导.第4节将根据推导的结果进行数值试验,并对结果进行分析,验证这一直接方法在求解量子控制问题上的高效性.第5节将对本文内容进行小结及展望.

1 一种量子控制问题模型及EL方程

本节主要介绍把激发态解操控至基态解的一种量子控制问题模型,并运用相关变分法理论找出对该模型解满足的EL方程.

1.1 一种量子控制问题模型

近年来,不少学者对量子控制问题进行了研究,其中Ulrich Hohenester等在量子控制理论中寻找控制参数λ(t)的时间变化,讨论了如何最优地把激发态解操控至基态解这一特殊量子控制问题,并提出如下量子控制问题的模型[21]：

(1)

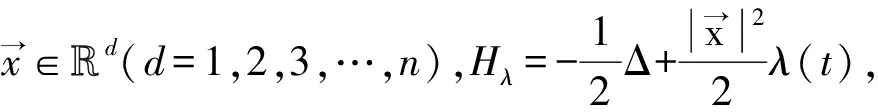
1.2 量子控制问题(1)满足的EL方程

(2)

因ψ和p是复数,所以将之改写

(3)

这里,

(4)

为求出泛函(3)的变分导数(或微分),先引入一般线性空间中的泛函导数的定义[24]：

设X是线性空间,Y是赋范空间,给定T：X→Y,∀x∈X,T(x)∈Y,定义在定义域D⊂X,值域R⊂Y.

定义：设x∈D⊂X,且在X中取一个h,若极限

(5)

存在,则其被称为T在X处增量为h的Gateaux微分.如果∀h∈X极限(5)都存在,那么变换T在x处是Gateaux可微的.

推论：若泛函T(x)∈,x∈X,T的Gateaux微分存在,则

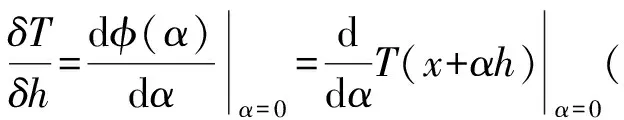
(6)

对泛函(3),利用变分原理[19]及上面的泛函导数的定义(6),有

其中,

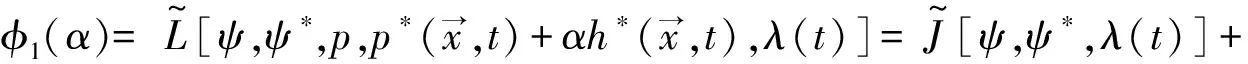
(7)

故

(8)

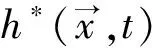
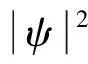
(9)

其中,

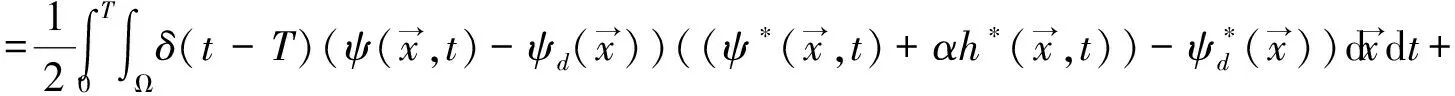
(10)

故

(11)

同理,

(12)

对方程(12),假设p是一个连续的函数,考虑在很短的时间Δτ对其两边关于T进行积分

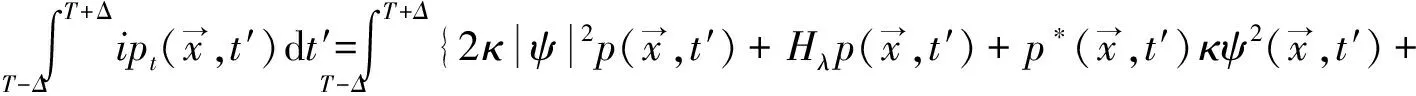
(13)

取Δτ趋近于0的极限,通过p的连续性,方程(13)的左边会趋近于0,右边的前3项也会趋近于0.但是,t中的δ函数在这个极限下产生了最终的时间条件：

(14)

(15)

故

(16)

对任意的h(t),有

(17)

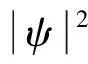
(18)

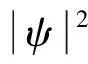
(19)

(20)

前人在设计数值方法时,通常基于EL方程(18)-(20)来找量子控制原问题(1)的解.本文不采用此方法,下一节介绍了一种直接离散方法.

2 量子控制问题的直接离散

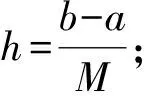
2.1 离散方法

(21)

(22)

在点(xj,tn)上进行直接离散,时间t方向采用最简显格式(或向前Euler法),空间x方向采用二阶中心差分,即

(23)

(24)

(25)

2.2 求解过程

基于上节内容,得到求一维量子控制问题(1)的具体过程为：

(3)计算xj=a+jh(j=0,1,2,…,M),以及tn=nΔt(n=0,1,2,…,N).

(4) 初始条件和边界条件的离散形式为(25).

(5) 方程(22)的离散形式为(24),泛函J(ψ,λ)的离散形式为(21).

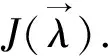
(7)利用fminunc得到函数ψ(x,t)在节点(xj,tn)处的近似值及λ(t)在点和tn处的近似值,输出结果.

3 数值结果分析

首先考虑κ=10,x0=1时,对γ取不同的值,对不同的v(x,λ(t))进行结果分析：

从图1-3可知,无论势函数v(x,λ(t))为哪一种形式,随着γ的减小T时刻得到的ψ(x,T)的值均与期望的ψd越来越接近,说明此方法在求解量子控制问题上具有一定的高效性.

再考虑γ=0.01,x0=1时,考察κ取不同的值的影响,并针对不同的v(x,λ(t))进行结果分析：

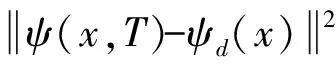
(a)λ(t)的结果 (b)ψ(x,T)的结果图1 当时,取不同γ时得到的数值结果

(a)λ(t)的结果 (b)ψ(x,T)的结果图2 当时,取不同γ时得到的数值结果

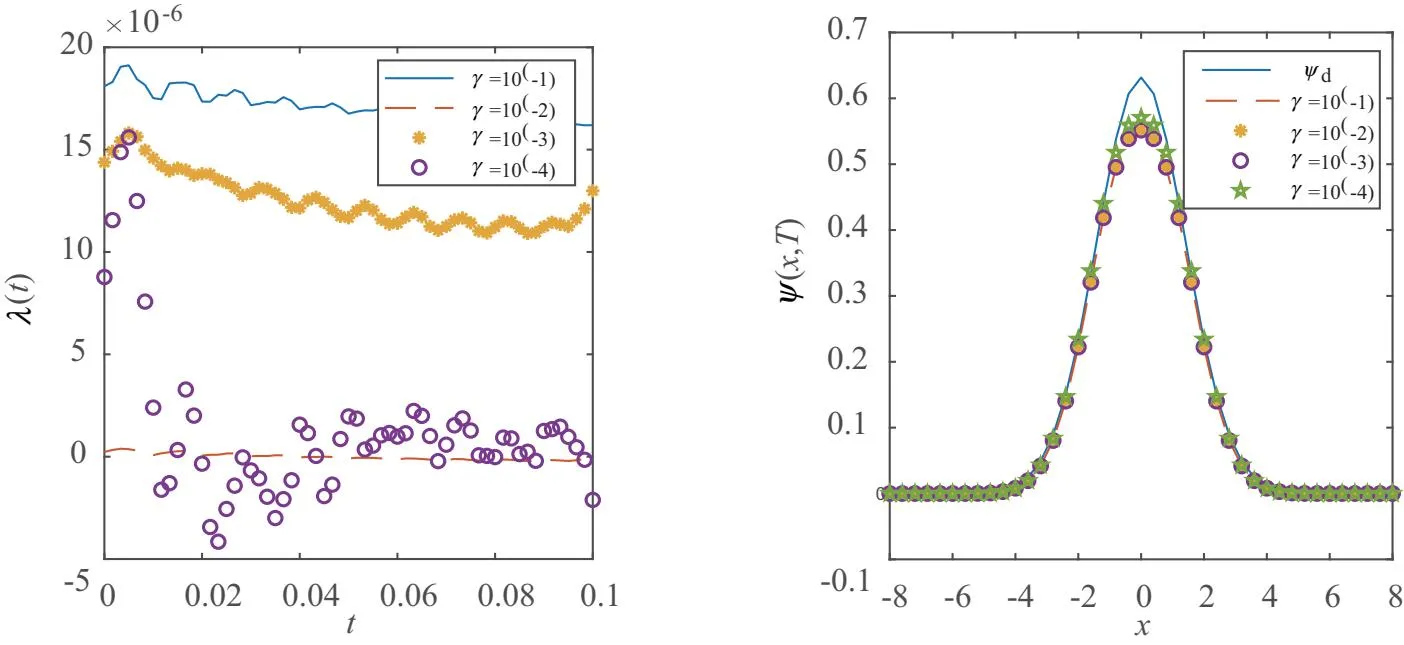
(a)λ(t)的结果 (b)ψ(x,T)的结果图3 当时,取不同γ时得到的数值结果

(a)λ(t)的结果 (b)ψ(x,T)的结果图4 当时,取不同κ时得到的数值结果

(a)λ(t)的结果 (b)ψ(x,T)的结果图5 当时,取不同κ时得到的数值结果

(a)λ(t)的结果 (b)ψ(x,T)的结果图6 当时,取不同κ时得到的数值结果

4 小结与展望

在本文中,理论上我们用相关变分法理论推出量子控制问题满足的Euler-Lagrange方程.数值上主要考虑了一维量子控制问题中一种特殊而又相对重要的情况：如何最优地把激发态解操控至基态解.针对此问题,提出一种直接离散方法：先把连续性泛函及约束条件离散,使量子控制泛函极小值约束问题转化为普通的优化问题,然后采用普通的优化方法求解.重点讨论对一维量子控制问题进行直接离散,把量子最优控制问题转化为普通的优化问题,在求解过程中,大大简化了计算量.基于γ和κ的值的变化,运用MATLAB 编写程序将其所得的数值结果与期望结果进行比较,验证了这一直接离散方法在求解此类问题模型具有一定的高效性.

针对本文所考虑的问题模型,仍有很多方面值得我们做进一步研究：还可以考虑高维问题的直接离散,泛函及约束条件的直接离散还可以考虑高阶高效的数值方法时间分裂谱方法等.相信未来,这一直接离散方法可以在更一般的控制模型问题中得到更加广泛的应用.