基于改进CRITIC-TOPSIS的电能质量评估方法
2024-02-05谢宗效杨留方曹伟嘉毛玉明
谢宗效,杨留方,曹伟嘉,毛玉明
(云南民族大学 电气信息工程学院,云南 昆明 650504)
随着电力系统引入了大量的非线性和其他负荷,目前电能质量问题日益严重[1].近年来随着技术的快速发展,用户侧设备对电能质量问题愈发敏感[2-3],所以,对于电能问题的治理和电价的分级收费,电能质量的综合评估具体重要作用.
电能质量的合理评估,确定权重和构建合理的评估模型是关键一环[4].文献[5]根据多个专家意见,各项指标的权重通过AHP确定从而评估电能质量.文献[6]采用多目标决策方法和模糊层次分析法(主观赋权法)来评估电能质量.文献[7]通过对熵权法的改进,使最终评估结果不会因为微小的差距而引起成倍的变化.文献[8-9]采用 DEA方法对客观数据进行分析,从而得到评估结果,但未考虑指标之间的相关程度以及可靠性差.文献[10]采用CRITIC法确定电能质量指标权重,并采用逼近理想解排序法进行排序,评估结果相对合理.但指标冲突性、相关性和重要性程度方面存在一些问题.
当前对电能质量综合评估的方法,文章提出了一种基于改进CRITIC算法优化权重和通过加权广义马氏距离代替欧式距离改进的TOPSIS法对电能质量开展综合评估,得到的权重值和评估结果更加客观准确.用本文的模型对某供电地区的电能质量监测点数据进行评估,最后计算的结果以及对比其他方法,说明基于改进CRITIC法和TOPSIS的电能质量综合评估方法有合理性.
1 质量评价指标体系
1.1指标体系构建
为了评估结果的真实和准确,指标体系的合理构建是电能质量评估的重要一步.通过对电能质量特点和现实条件的分析以及指标彼此之间差异性和内在关系的考虑,把电压波动、电压偏差、电压暂降、电压谐波、三相不平衡、频率偏差、供电可靠性和服务性指标纳入电能质量评估指标,结合传统指标和可靠服务性指标,能够得到更加准确、全面和接近实际的评估结果.电能质量综合评估指标体系如图1所示.
1.2 标准化处理
1.2.1 国家相关标准
根据国家有关标准将电能质量划分为五个等级[11],I-V 分别表示优秀、良好、中等、合格、不合格,各电能质量等级中的单个指标值如表1所示.
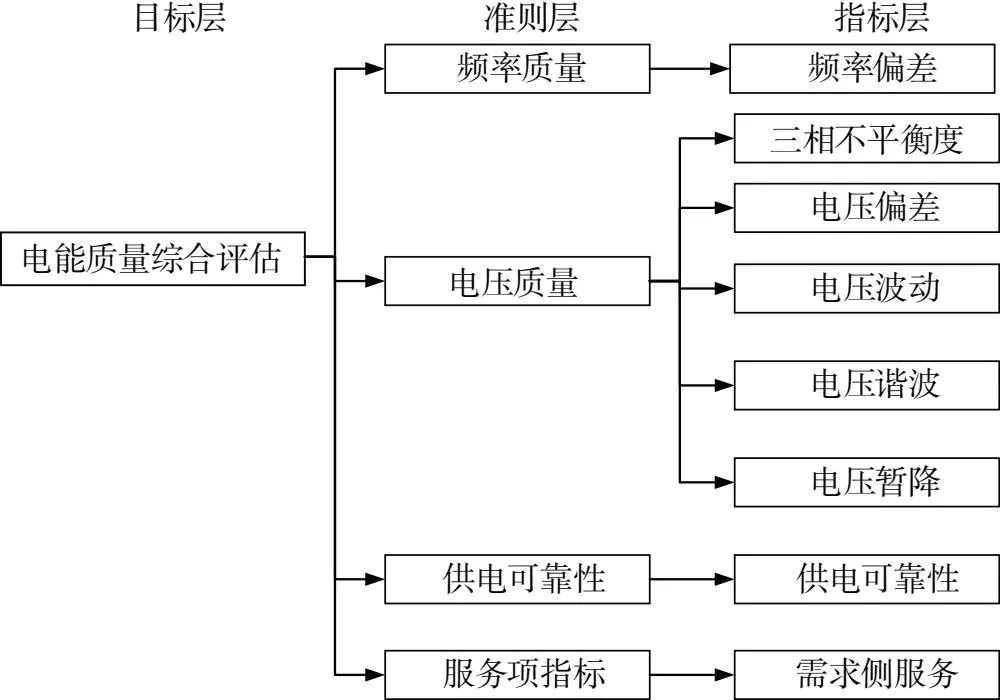
图1 电能质量综合评估指标
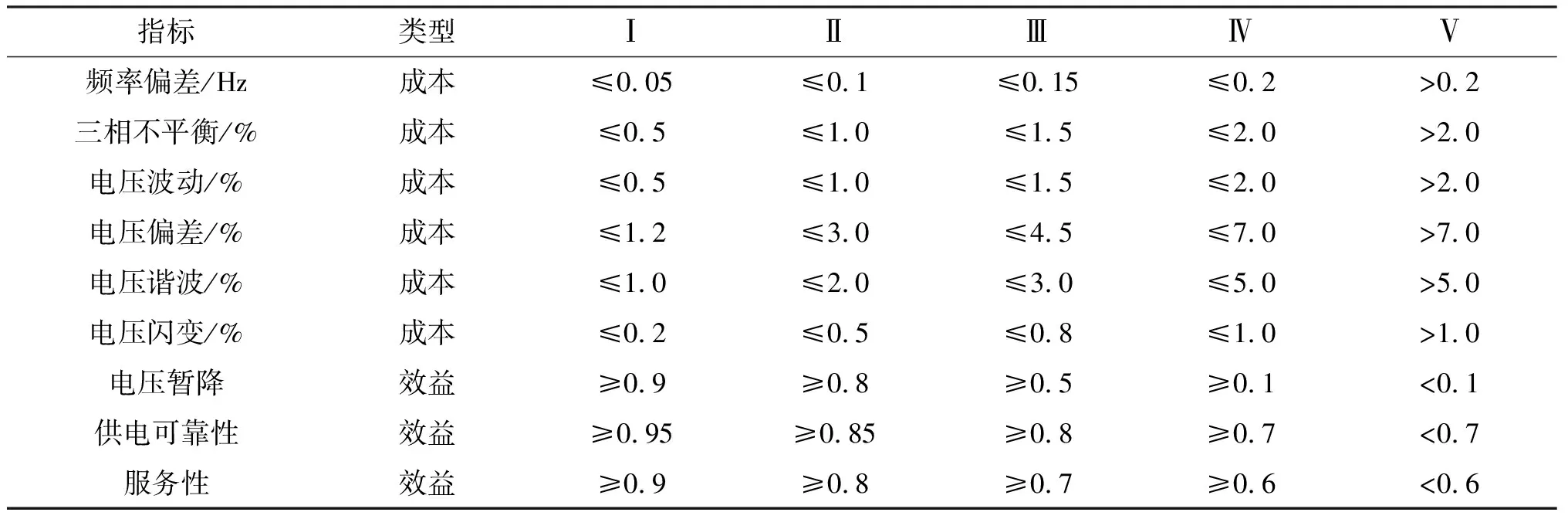
表1 电能质量指标分级情况
1.2.2 标准化处理
1) 效益型指标和成本型指标
效益型指标
(1)
成本型指标
(2)
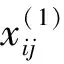
2) 指标数据标准化处理
因为各个指标量纲不同,可能影响到评估结果的准确性,所以需要对指标进行标准化处理,标准化过程如式(3)所示.
(3)
2 决策模型
2.1 改进CRITIC法计算权重
CRITIC法是一种客观赋权法,学者Diakoulaki于1995年率先提出,通过指标的对比强度和冲突向来表明信息量,根据信息量来确定指标的客观权重[12].这个方法的计算公式存在一些不足,文献[13]进行了改进,第一是用标准差系数来衡量辨别力,第二是通过对相关系数取绝对值来更准确的反应冲突性问题.
其具体步骤如下:
1) 建立规范评估矩阵
假设有n个监测点,m个评价指标.将两者一一对应,便可得到初始评判矩阵.考虑到指标间的量纲和数量级不同,需要对矩阵进行规范化处理.
运用式(1~3)各指标进行无量纲处理.
2)计算冲突性.
相关系数表示指标之间的相关性,取值越大,相关性越强,根据式(4)求取评价指标之间反映相关性的相关系数rij
(4)
然后相关系数组成相关系数矩阵,根据相关系数矩阵可求得冲突性cj,计算公式如式(5)所示
(5)
3)计算对比强度
用标准差系数来表示对比强度,计算公式如式(6)所示
(6)
式中:σi表示评估矩阵中第j个列向量均方差.
4) 计算指标之间的信息量
根据对比强度与冲突性概念,定义信息度衡量指标Ci,计算公式如式(7)所示
(7)
Ci的取值越大,也就说明信息量越大.
5)计算权重
由上述所求数据可得第j个指标的客观权重,计算公式如式(8)所示.
(8)

图2 CRITIC法流程图
2.2 加权广义马氏距离改进 TOPSIS算法评估模型
TOPSIS法是由Hwang和Yoon首先提出,是一种在解决多属性问题中比较实用的方法[14].通过求解欧式距离得到相近贴进度进行方案的排序评估,但是欧式距离存在指标变量之间的相关性干扰,从而影响评估结果.用数据的协方差距离表示马氏距离,数据之间的相关性问题得以解决,但协方差矩阵不可逆的问题以及指标的重要性差异未被考虑进去,因此考虑用加权广义马氏距离[15]代替欧式距离,从而使得到的结果更加合理.
基于广义加权马氏距离改进TOPSIS方法基本步骤如下:
1)构建包含m个监测点,n个指标标准化矩阵
(9)
2)确定正理想解F+与负理想解F+,计算公式如式(10-11)下:
F+=max1≤i≤mxij,
(10)
F-=min1≤i≤mxij.
(11)
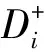
(12)
(13)
4)计算各监测点相对理想解的贴近度Ci,计算公式如下:
(14)
5)进行方案排序,贴近度的值越大,方案越优.
计算流程如图 2 所示.
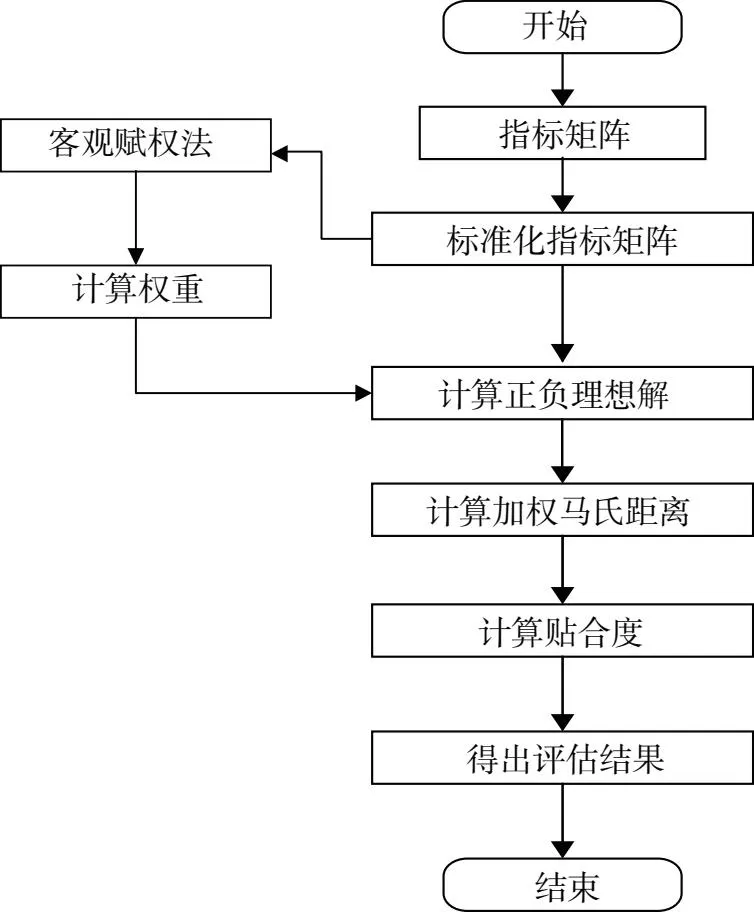
图3 计算流程图
3 算例分析
选取某个观测地域内5个不同观测点[16],获得了各监测点指标的数据如表2所示.
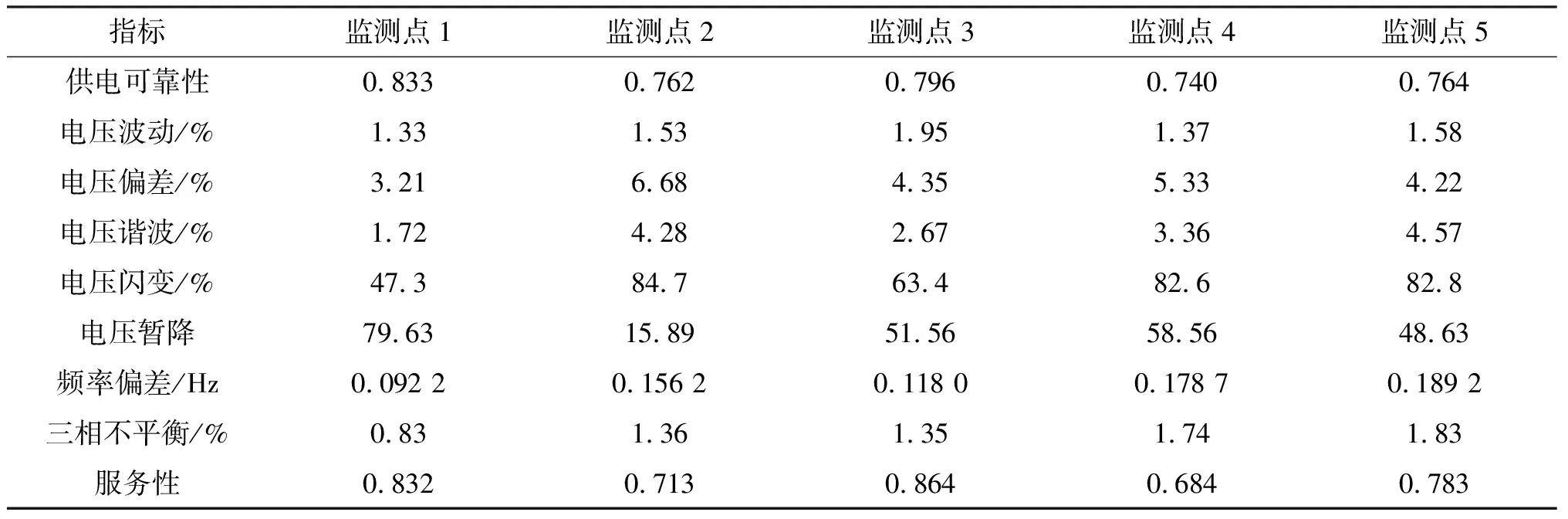
表2 监测点指标数据
3.1 计算过程
1)按式(1)~(3)对表 2 中的数据进行标准化处理,得标准化矩阵:
2)确定指标权重
采用改进CRITIC,按式(4)~(8)计算得各指标权重w=(0.011 9,0.124 8,0.206 0,0.356 4,0.016 3,0.157 7,0.034 9,0.048 6,0.043 3).
3)计算正负理想解
根据式(10)~(11)可得各监测点的正负理想解分别为
F+=(0.319 6 0.289 7 0.324 5 0.382 4 0.331 8 0.387 9 0.338 0 0.351 4 0.343 5),
F-=(0.283 9 0.182 2 0.027 4 0.027 4 0.282 7 0.077 4 0.257 6 0.240 6 0.271 9).
4)计算加权广义马氏距离
根据式(12)~(13)计算 5个监测点到“正理想解”的距离D+和“负理想解”的加权广义马氏距离D-分别为:
5)计算贴近度
根据式(14)得到 5个监测点的贴近度分别为:
C1=0.991 9,C2=0.259 7,C3= 0.343 5,C4=0.401 2,C5=0.490 0.
3.2 结果分析
由上述计算结果可得5个监测点的贴近度大小排列为:监测点1>监测点5>监测点4>监测点3>监测点2,监测点1的电能质量较优.分别算取传统TOPSIS法、马氏距离改进TOPSIS法和广义马氏距离改进TOPSIS法的贴近度以及本文所用方法的贴进度,详细结果见表3.并对贴进度排序,结果见表4.

表3 不同计算方法的方案贴进度

表4 不同计算方法的方案排序
从结果可以看出,监测点的相对排序性大体上一致,特别是与传统TOPSIS法的排序只有监测点4、5有分歧,说明本文使用方法的可信性.考虑到指标之间的重要性差异和相关性等问题和多方面因素,可认为本方法更准确.
4 结语
电能质量综合评估反映的是电力系统所提供电能整体的质量水平,根据评估结果可以合理治理和按质定价,同时也可以为供用双方明确质量责任提供依据.本文构造CRITIC-TOPSIS模型,提供了一种比较合理的电能质量评估方法.
1)通过参考相关文献和询问专家,再综合对电能质量特点的考虑,最后确定电能质量评估指标体系由电压波动、电压偏差、电压暂降、电压谐波、三相不平衡、频率偏差、供电可靠性和服务性指标这些指标构成.
2)考虑避免人为因素的影响,采用CRITIC法对数据分析计算指标权重,得到更加现实和科学的权重结果.
3)加权广义马氏距离替代欧式距离对TOPSIS法进行改进应用到电能质量综合评估中,在相关文献中尚未发现此方法在电能评估中的应用.评估模型解决了协方差矩阵不可逆的问题以及指标之间的重要性差异和相关性问题,使评估的结果更科学合理,最后实例分析结果表明方法的可行性.
