基于轻型自限制注意力的结构光相位及深度估计混合网络
2024-02-05朱新军赵浩淼王红一宋丽梅孙瑞群
朱新军,赵浩淼,王红一,宋丽梅,孙瑞群
(天津工业大学 人工智能学院,天津 300387)
1 引言
光学三维测量是光学计量和信息光学中最重要的研究领域和研究方向之一[1]。结构光三维测量技术是光学三维测量的重要方式[2],具有速度快和精度高等优点,在机器人引导、虚拟现实、人机交互、文物保护、机器人视觉、生物医学等领域有相当广阔的应用前景[3]。在过去的研究中,可以把传统的结构光相位提取技术主要分为两类:以傅立叶变换法为代表的单幅图相位提取方法[4]和相移方法[5]。傅立叶算法只需要单个条纹图案并可直接获得包裹相位图。该方法受物体运动影响的程度较低但存在相位提取精度较低和计算时间长等问题。相移算法至少需要3 幅条纹图像[6],通过相移计算获得相对相位图。该方法对于投影光栅的标准性和相移量准确度的要求较高。其精度高但受运动环境影响较大。以上方法获得的相位通常为包裹相位,需要通过一些展开方法将相对相位图变换为绝对相位[7]。此外,在结构光深度估计方面,传统方法需要进行系统标定、相位深度映射完成深度测量与三维测量。
综上所述,准确的条纹相位估计与深度估计是结构光测量的主要挑战。近年来,在结构光三维重建领域中出现了许多基于深度学习的方法。Feng 等人通过实验证明深度神经网络可以显著提高单个条纹图案的相位估计精度[8],具体来说,通过卷积网络预测中间结果,最终得到高精度相位图。Nguyen 等人提出了一种端到端的方法,使用全卷积网络由条纹图得到深度图[9]。Jeught 等人提出了一种完全基于深度学习的从单个变形条纹图案中提取深度信息的方法[10]。张钊等人提出了一种多阶段深度学习单帧条纹投影的三维测量方法,通过分阶段学习方式依次获得物体的深度信息[11]。其中,大部分结构光相位估计方法都基于卷积网络,不利于上下文信息的特征捕获,而Transformer 的优势是利用注意力的方式捕获全局的上下文信息,以对目标建立远距离依赖,提取有力的特征。文献[12-14]对这两种网络进行优势互补[12-14]。Zhu 等人开发了一种混合CNN-Transformer 模型,该模型通过条纹级次预测进行相位展开[15],在条纹级次预测方面取得了较好的效果。
本质上,基于深度学习的相位估计和深度估计都属于回归预测问题。目前上述的模型虽然取得了较好的效果,但存在较大的误差,仍有可提升的空间。为此,本文提出了一种CNN-Transformer 相结合的模块,分4 个阶段应用在U 型总体架构中,将局部特征与全局特征相融合,并更新了注意力机制的算法,在网络中使用轻型自限制注意力(Light Self-Limited-Attention,LSLA)机制以节省计算成本和参数数量。最后,将所提出的网络在结构光深度估计和相位估计两个任务中都进行了实验。
2 条纹投影轮廓术原理
典型的条纹投影轮廓术(Fringe Projection Profilometry,FPP)系统由投影仪和相机组成[16],图1 为FPP 系统原理图,投影仪将条纹图案投影到目标物体上,变形的条纹包含了物体的特征信息,然后由相机捕获并输出数字图像。在多频率的FPP 中,投影仪会投射多个不同频率的条纹图案,相机捕获多张图片,然后通过相位解算得到物体表面的三维形状信息。
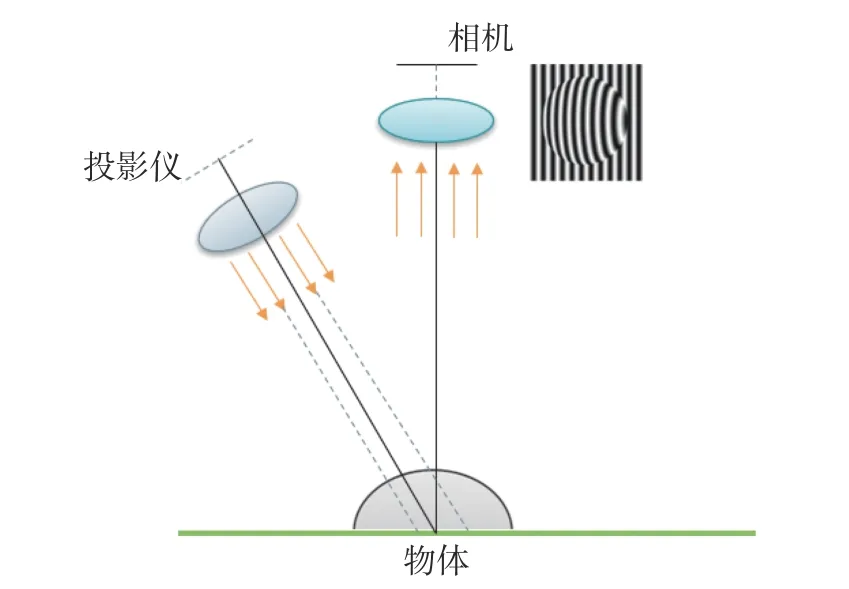
图1 FPP 系统原理图Fig.1 Schematic diagram of the FPP system
通过分析捕获的变形条纹,解出相位跳变的包裹相位。图像中的条纹可以表示为:
其中,In(x,y) 为某一像素点 (x,y) 的光强,A(x,y)为该像素点的背景光强,B(x,y)为该点的调制光强,φ(x,y) 为该点的相位值,n=0,1,···,N-1,为相移的步数。根据公式(1)计算出包裹相位:
包裹相位存在 2π的相位跳变。为得到连续的相位信息,需要将相位跳变的包裹相位展开,相位展开公式如下:
其中,ϕ(x,y) 是展开相位,k(x,y)是条纹级数。
根据标定相位与三角坐标的关系,可以得到绝对相位,根据绝对相位可以直接获取三维高度信息。
3 基于轻型自限制注意力的混合网络
3.1 总体结构
网络的总体结构是U 型结构,网络结构图如图2 所示。其由一个编码器-解码器组成。该模型的输入是结构光图像,在编码器网络中,通过下采样方式将输入图像的分辨率降低,提取低分辨率特征,经过4 次下采样后,进入解码器网络,再进行相同次数的上采样操作,将编码器学习的低分辨率特征映射到高分辨率像素空间中。该模型还使用了跳连接,在解码器网络中将浅层特征和深层特征相融合,从而提高边缘信息的精细度。
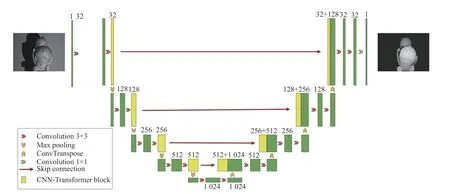
图2 网络结构图Fig.2 Network structure diagram
太窄的网络每一层能捕获的模式有限,此时即使网络再深也不可能提取到足够信息往下层传递。加宽网络可以让每一层学习到更丰富的特征,比如不同方向,不同频率的特征。但宽度增加会导致计算量成平方数增长。考虑到效率问题,要适当调整网络宽度。经实验发现,把网络加宽到1 024 时效果最优。
3.2 CNN-Transformer 相结合模块
CNN 是一种前馈神经网络,它的特点是卷积层和池化层交替使用,其可以直接处理高维数据,自动提取图像的特征信息,提高模型的计算效率,但不利于上下文信息的特征捕获;Transformer 是一种基于自注意力机制的神经网络模型,可以学习全局信息,提高模型的表达能力。在结构光图像处理过程中,由于图像数据的维度较高,使用传统的Transformer 模型会导致计算量过大,将CNN 和Transformer 结合可以提高模型的计算效率,同时将CNN-Transformer 的优势相结合,使用CNN 提取图像的局部特征,Transformer 学习图像的全局信息,局部特征与全局特征相融合,提升模型的表达能力。基于此,本文在CMT[17]的基础上进行了改进,模块可分为3 个部分,模块的结构图如图3 所示。
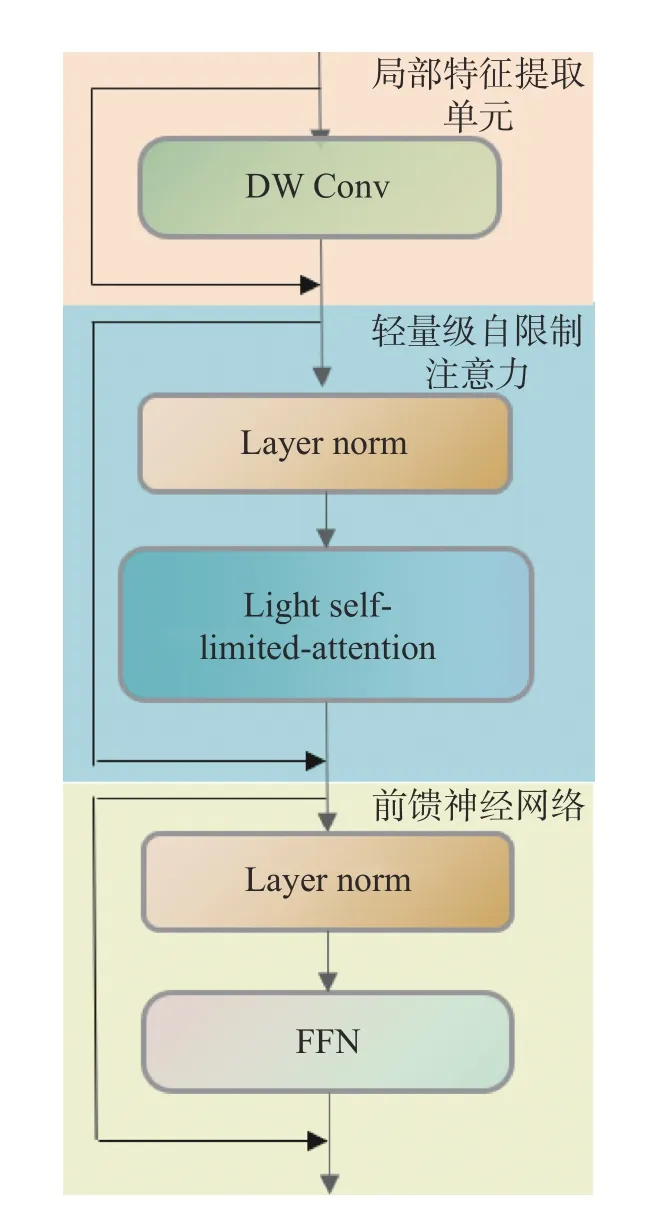
图3 CNN-Transformer 模块结构图Fig.3 Structure of the CNN-Transformer module
3.2.1 局部特征提取单元
由于Transformer 的特性可能会忽略图像的部分局部信息,为了更有效地提取图像的局部特征,使用深度卷积提高网络的非线性能力和网络的表达能力,如公式(4)所示:
其中,LFE代表局部特征提取单元,x∈RH×W×d,H×W是当前阶段输入的分辨率,d表示特征的维度,DWConv表示深度卷积。深度卷积完全是在二维平面内进行。这种运算对输入层的每个通道独立进行卷积运算,可以减少卷积的计算量,高效获取图像的局部信息,但存在不能有效利用不同通道在相同空间位置上的特征信息的问题,由于输入的结构光图像是单通道,故可以避免深度卷积存在的这个问题。
3.2.2 轻量级自限制注意力
Transformer 可以有效地学习图像的全局特征,然而在结构光图像处理中,数据的维度通常很高,使用全局自注意力的计算成本非常高。本文通过LSLA 机制[18]进行全局特征的提取,将全局自注意力分解为局部和全局两个部分,并使用位置信息模块以及限制注意力模块来增强位置信息以及控制注意力权重大小。在减少计算量的同时还可以利用图像的空间结构信息,从而对位置信息进行更好的建模。
在传统的自注意力机制中,键值对通常表示不同的语义信息。例如,在自然语言处理中,键可能表示输入句子中的不同单词,而值则表示与这些单词相关联的特征向量。在图像领域,键和值通常表示不同的位置特征和图像特征。然而,在LSLA 机制中,由于涉及图像信息的处理,因此,将键值对替换为输入X,这样可以有效减少计算成本和模型参数量。此外,在图像处理时,相邻像素通常具有相似的特征,这也使得使用相同的输入 X 作为键和值是可行的。这可以显著减少 LSLA机制的计算成本,并使其适用于需要高效处理的应用场景。
LSLA 机制包含位置信息模块和限制注意力模块。位置信息模块使用了一个自适应的位置编码向量,增强了位置信息的表达,可以更好地处理输入数据中位置信息的变化。限制注意力模块可以控制注意力权重的大小,避免出现过于集中的注意力分布,从而提高了模型的鲁棒性和泛化能力。具体来说,在LSLA 机制中,对于每个输入位置,首先使用一个局部自注意力模块计算局部上下文信息。然后,使用一个全局自注意力模块计算全局上下文信息,再进行融合,得到最终的特征表示。另外,限制注意力模块在softmax 函数之后使用外部位置偏差来限制一些较大的注意力权重值。内外部位置偏差和动态尺度相互配合,LSLA机制的公式定义为:
其中,X为原始输入数据,Q是查询矩阵,DS表示查询块附近的块具有较大的动态尺度和内部位置偏差值,Bi和B0分别是内部位置偏差和外部位置偏差。
3.2.3 前馈神经网络
模块的最后一部分使用比较简单的前馈神经网络(Feedforward Neural Network,FFN)。FFN 的信号从输入层到输出层单向传递,网络的目标是通过调整权值使预测输出与实际输出之间的误差最小。使用的FNN 包含两个线性层和一个GELU激活函数。第一个线性层将输入的尺寸扩大4倍,第二个线性层以相同的比例进行尺寸缩小。这种缩放操作有助于保留有用的信息并去除不必要的信息,中间使用GELU 激活分离,因为GELU在负数输入下更具有平滑性。
4 实验与结果
为了证明所提出的网络对于结构光图像处理的有效性,本文进行了两种实验:结构光相位估计(利用条纹图像预测包裹相位)和深度估计(利用条纹图预测深度图),并且在真实数据集和仿真数据集上分别做了实验。所提出模型的深度学习框架为Pytorch,实验GPU 为24 GB 内存的NVIDIA GeForce RTX3090。
4.1 结构光相位估计实验
4.1.1 数据准备
在结构光图像到包裹相位的预测实验中,本文使用的真实数据集和仿真数据集都由1 000 个样本组成。本论文使用的是由Blender 生成的仿真数据集和Feng 等人制作的真实数据集[8],部分数据示例图如图4 所示。每个样本的大小均为640 × 480,按照8∶1∶1 的比例划分训练集、验证集和测试集。实验以输入结构光图像,计算高精度的包裹相位为最终目标。

图4 部分数据示例图。第一行为仿真数据,第二行为真实数据。(a)仿真条纹图;(b)仿真条纹图D;(c)仿真条纹图M;(d)仿真条纹图包裹相位;(e)真实条纹图;(f)真实条纹图D;(g)真实条纹图M;(h)真实条纹图包裹相位Fig.4 Sample maps in some datasets.The first lines are simulation data,the second lines are real data.(a) Simulation fringe map;(b) simulation fringe map D;(c) simulation fringe map M;(d) simulation fringe wrapped phase;(e) real fringe map;(f) real fringe map D;(g) real fringe map M;(h) real fringe wrapped phase
在大多数相位解调技术中,背景强度A(x,y)被视为干扰项,要从总强度中去除。根据公式(2)可以将包裹相位公式简化为:
其中,c是取决于相位解调算法的常数(傅立叶方法中c=1/2,N步相移法中c=N/2),M(x,y)和D(x,y) 分别表示分子项cB(x,y)sinφ(x,y)和分母项cB(x,y)cosφ(x,y)的简写。
从结构光图像预测包裹相位有直接预测包裹相位及先预测出分子项D 和分母项M,再通过公式(6)对包裹相位进行计算两种方式。由于相位信息通过反正切运算被约束在-π 到π 之间,因此,包裹相位会存在2π 的跳变。直接使用深度学习方法难以精确预测跳变位置,而通过预测中间变量D 和M 的方法不存在跳变,因此,利用D 和M 可以获得更高质量的包裹相位。实验中,使用UNet 网络对这两种方式进行训练,比起直接预测包裹相位,通过训练得到D 和M 再计算包裹相位的预测精度提升了约60%。对于单输入双输出任务,需要预测的D 和M 有强关联性,在原本网络的基础上添加一个分支对结果准确率略有提升,而且双输出模型只需要训练一次,减少了训练时间,结果见表1。因此,本文把实验的重点放在同时预测D 和M 上。
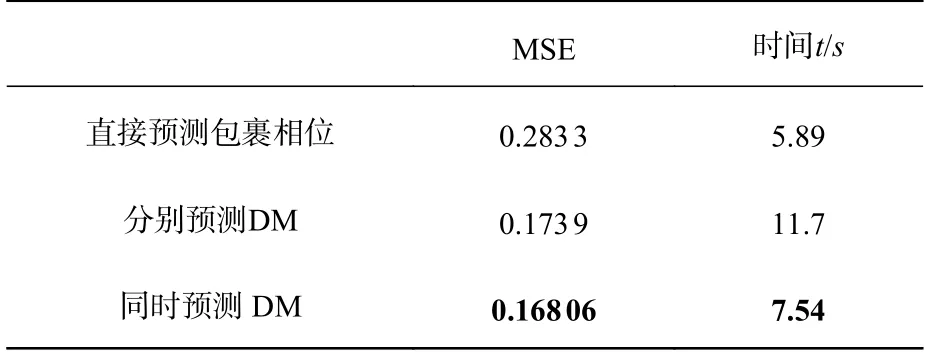
表1 不同包裹相位计算方法比较Tab.1 Comparison of the different wrapped phase calculation methods
4.1.2 实验结果分析
在计算预测结果的损失时,背景误差也会算入其中并且对结果有较大影响,而研究的重点应该在有条纹部分的物体上。所以,本文提前批量制作了测试集的背景模板,以便获得更准确的实验结果。使用由同一频率的四步相移获得的条纹图制作背景模板。
相移法的实现一般需要使用投影仪向被测对象投射多张固定位置的光栅条纹图像,同时使用相机采集。利用N 步相移法经被测对象调制后的变形条纹公式如式(7)所示,数据均由四步相移所得,I0(x,y)、I1(x,y)、I2(x,y)、I3(x,y)分别为相移0、π/2、π、3π/2 后的光栅图像,可得到背景模板A(x,y),公式如下:
得到背景部分后,将背景部分设置为一个恒定值(实验中背景部分为1),将模板和预测的包裹相位进行比较,然后去掉包裹相位图的背景部分,可使得到的包裹相位部分的损失更准确。
本文使用Unet[19]、DPH[20]、R2Unet[21]、SUNet[22]等网络在相同数据集上进行训练。得到D 和M 后,根据公式(7)得到包裹相位后计算损失值,结果见表2。从表2 可以看出,本文模型提高了包裹相位预测的精度,预测时间较UNet 和SUNet 长,较其他网络短。图5(彩图见期刊电子版)显示了所提出网络与其他网络的比较结果及局部放大图。从局部放大图可以看出,在相位边缘及物体不连续处,本文方法比其他方法预测结果更接近标签数据。为了更直观地比较5 种网络的预测结果,绘制了预测得到的包裹相位图的第200行曲线图,如图6(彩图见期刊电子版)所示。可以看出所提出模型得到的结果细节信息比其他网络更加接近标签。
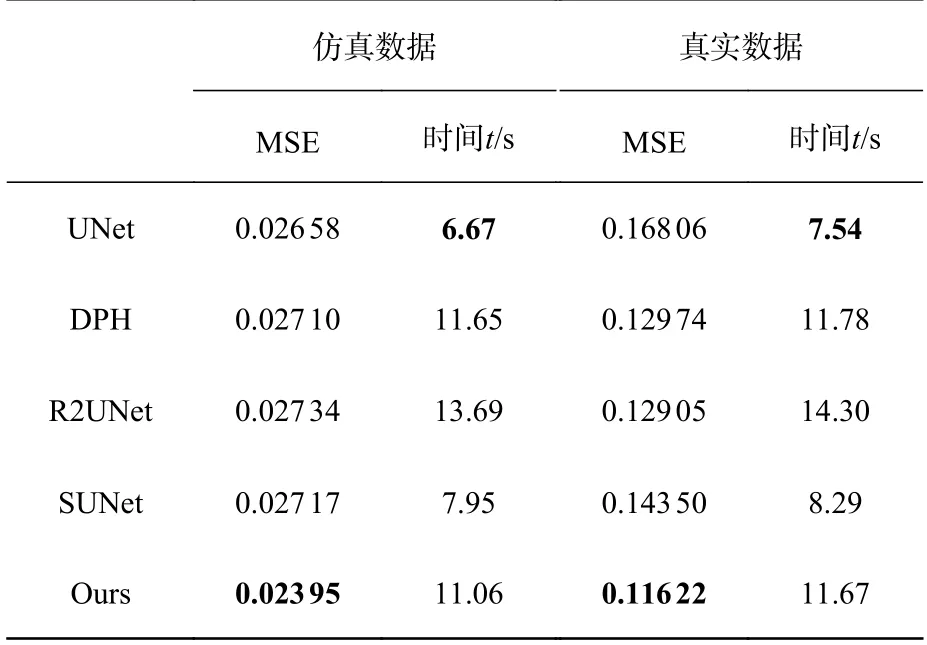
表2 包裹相位预测方法比较Tab.2 Comparison of the wrapped phase prediction methods
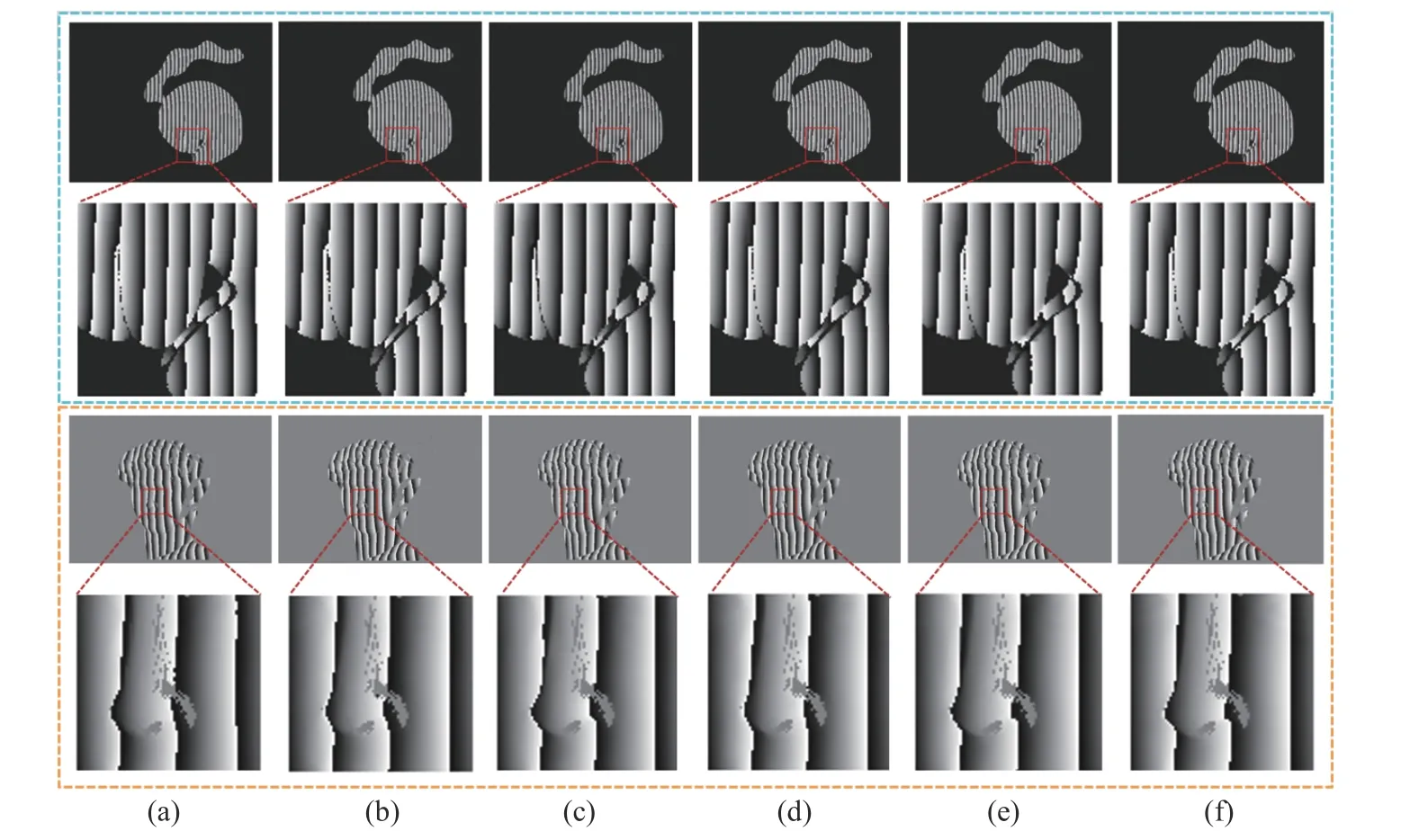
图5 不同网络仿真和真实数据包裹相位对比。蓝色框为仿真数据,橙色框为真实数据。(a)UNet;(b)DPH;(c)R2UNet;(d)SUNet;(e)Ours;(f)标签Fig.5 Comparison of different network simulation and real data wrapped phases.The blue boxes are the simulation data,and the orange boxes are the real data.(a) UNet;(b) DPH;(c) R2UNet;(d) SUNet;(e) Ours;(f) Label
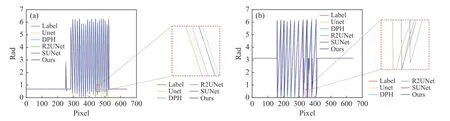
图6 包裹相位结果曲线图。(a)仿真数据结果比较;(b)真实数据结果比较Fig.6 Wrapped phase curves.(a) Comparison of simulation data;(b) comparison of real data
4.2 结构光深度估计实验
4.2.1 数据准备
由于公开的结构光深度数据集比较少,本文使用Blender 制作部分仿真数据集[23],生成数据集的流程如图7(彩图见期刊电子版)。Blender 可以通过调整对象模型、相机和投影仪来模拟真实世界的场景,使用相机捕捉和渲染物体图像并输出深度图。
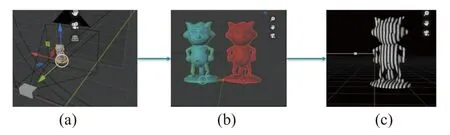
图7 生成数据集流程图。(a) 模型导入;(b) 调整大小;(c) 投影条纹Fig.7 Flowchart of dataset generation.(a) Model import;(b) adjust of the model size;(c) projection fringe
生成数据集的具体步骤如下:将stl 格式的模型导入到Blender 中。选中导入的模型,使用变换工具调整它的大小和位置,以适应深度数据集的尺寸和视角。在Blender 中添加一个平面,将条纹图像贴在平面上,然后将相机对准模型和平面。确定相机的位置、方向、焦距等参数,以保证生成深度数据集的质量。在Blender 中安装“Structured Light Scanning”插件,设置条纹图像的参数和输出路径,然后点击“扫描”按钮开始生成深度数据集。在插件设置界面可以调整结构光的编码方式、条纹图像的数量和周期、相机参数等。点击“生成数据集”按钮,Blender 会根据这些参数生成深度图像数据集。
本文使用的真实结构光数据集是Nguyen 等人使用由相机和投影仪组成的FPP 系统重建的深度图[9]。将具有不同空间频率的一组条纹图案投影到目标物体表面上,捕获变形的结构光图案,计算相移条纹和深度图的相位分布。仿真数据集和真实数据集包含540 张灰度图像,图像大小是640 × 480,按照8∶1∶1 的比例划分训练集、验证集和测试集,部分数据示例图像如图8 所示。

图8 部分数据示例图。(a)仿真条纹图;(b)真实条纹图;(c)仿真深度图;(d)真实深度图Fig.8 Sample maps in the dataset.(a) Simulated fringe map;(b) real fringe map;(c) simulation depth map;(d) real depth map
4.2.2 消融实验
为了证明所提出的网络结构确实有效,本文在真实数据集上进行了消融研究,逐步修改模块结构并评估结果。首先,在CMT 模块进行实验并把它作为基线模型,将CMT 模块中的注意力机制改为LSLA 机制;然后,将CMT 模块中最后的部分换为较为简单的FFN;将CMT 模块放到U 型结构中,分为4 个阶段的上采样和下采样,每个阶段的CMT 模块重叠两次。
实验结果如表3 所示,通过替换注意力机制和改善网络的总体结构,网络性能得以逐渐提高。具体地,将注意力机制替换为LSLA 后,MSE下降了18.9%,模型预测时间也略有减少;将CMT 原本的反向残差前馈网络替换为更为简单的FFN 后,MSE 几乎没有下降,但是预测时间减少了19.5%;最后把CMT 模块应用在U 型结构中,分为编码器和解码器逐步提取图像特征,结果表明放入U 型结构后精度提升了21%。
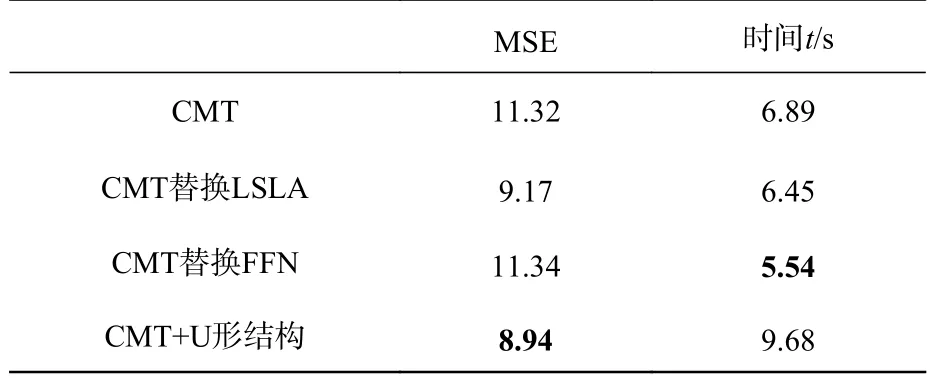
表3 消融实验结果比较Tab.3 Comparison of ablation experiment results
4.2.3 实验结果分析
对于结构光图像的深度估计性能评价,本文选用了几个有代表性的卷积网络和混合网络与本文提出的网络进行比较,在仿真数据集和真实数据集上进行实验,比较结果如表4 所示。从表4可以看出,所提模型的精度较其他几种网络高,模型预测的时间较DPH 和R2Unet 少,总体预测效率较高。图9(彩图见期刊电子版)显示了本文方法与其他网络在仿真数据集与真实数据上的视觉比较效果。前两行是仿真数据及结果,后两行是真实数据及结果。由图9 可以看出:相较其他网络,本文所提出的网络在边缘处理和细节处理方面更优,预测结果更接近真实标签数据。
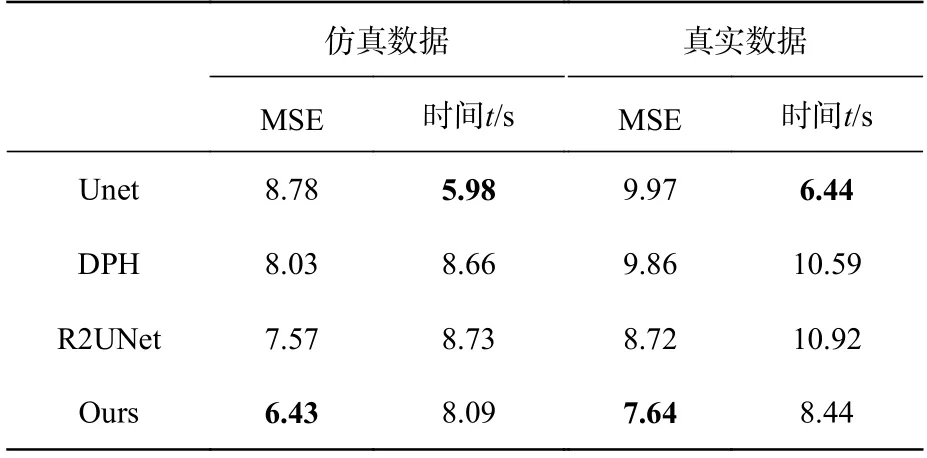
表4 不同方法深度估计结果比较Tab.4 Comparison of the depth estimation results by different methods

图9 不同方法深度估计视觉结果比较。蓝色框为仿真数据,橙色框为真实数据。(a) 输入数据;(b) UNet;(c) DPH;(d) R2UNet;(e) Ours;(f)标签Fig.9 Comparison of the visual results of depth estimation by different methods.The blue boxes are the simulation data,and the orange boxes are the real data.(a) Input data;(b) UNet;(c) DPH;(d) R2UNet;(e) Ours;(f) Label
5 结论
本文提出一种基于LSLA 的结构光估计混合网络,用于处理结构光图像的相关任务,如由结构光图像预测包裹相位、对结构光图像进行深度估计。所提出的网络使用U 型结构架构,分4 个阶段对结构光图像进行上采样和下采样,每个阶段都使用了两个重复的CNN-Transformer 模块。实验证明将LSLA 机制应用在结构光预测时可以减少预测时间,提高预测精度。为了评估所提出网络的性能,挑选了几个有代表性的网络分别在真实数据集和仿真数据集上做对比实验。结果表明:本文提出的网络可以提高结构光图像深度估 中,精度最高提升26%,在结构光相位预测实验计和相位估计的性能。在结构光深度估计实验 中,精度最高提升31%。
猜你喜欢
杂志排行
中国光学的其它文章
- Design of all-optical logic gate based on two-dimensional photonic crystal
- All-solid-state acousto-optic mode-locked laser operating at 660 nm
- Stimulated brillouin scattering in double-clad thulium-doped fiber amplifier
- Optical simulation design of surface mounted device beads for wide beam and high uniformity display
- 用于紫外光谱仪的探测器温度控制系统
- TDLAS 气体激光遥测高灵敏光电探测电路设计
