用于紫外光谱仪的探测器温度控制系统

蒋 雪，侯 汉，马庆军，林冠宇

（中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033）

1 引言

大气臭氧（O3）、平流层气溶胶等微量气体的密度和垂直分布情况，对气候变化和大气环境研究有重要价值。FY-3 紫外临边光谱仪是借助卫星平台观测地球临边大气紫外-可见波段太阳后向散射的光学遥感仪器。探测获得的光谱遥感信息对于农业、气候、军事等方面的发展具有重要意义[1-3]。

FY-3 紫外临边光谱仪，选用的是英国e2v 公司生产的背照式互补金属氧化物半导体（CMOS）探测器，测量范围是290 nm～500 nm 紫外波段。CMOS 探测器和电荷耦合器件（CCD）探测器性能相当，但是CMOS 探测器具有驱动时序复杂度低、开发周期短、成本低的优点。CMOS 探测器分为背照式和正照式两种。背照式CMOS 探测器的结构布局使其不受遮挡，故其比正照式CMOS 探测器接收光子的能力更强，灵敏度更高，更适合用于航天领域。因此，本文选用背照式CMOS 探测器。但是，由于背照式CMOS 探测器的工艺特殊，在常温条件下产生的暗电流较高，噪声较大，为了提高图像质量，需要将背照式CMOS 探测器置于低温条件下应用。除此之外，极速的温度变化产生的温度冲击可能会对背照式CMOS 探测器造成不可逆的损伤，导致探测器获取的图像出现大量的异常像素。这些异常像素的光响应情况不同于正常像素的感光情况，将影响图像质量。为了解决上述问题，本文设计了探测器温度控制系统，以使探测器的温度达到控制要求。

本文设计的探测器温度控制系统核心采用的是PID 控制。PID 控制算法是一种应用于过程控制的闭环控制算法，可以起到动态修正实测值与目标值之间偏差的作用，广泛应用于各种工业控制中的连续系统[4-5]。传统的温控系统是在硬件上搭建PID 控制单元，用模拟控制的方式调节探测器温度。这种模拟控制方式的灵活度很低，不易更改，调试难度较高[6-7]。本文设计的温度控制系统是基于FPGA 实现的数字PID 控制。这种数字控制方式灵活度很高，可以在软件界面预留参数输入入口。通过更改控制参数，灵活调整制冷目标温度、温变速度与温控精度，这种调节的灵活性大大提高了仪器的研制效率，而且在轨观测时，如遇突发状况也可以灵活应对。但是直接使用PID 控制算法会带来一些问题，比如，偏差过大引起的温度冲击问题[8-10]，积分饱和问题。本文通过加入输入过渡过程和抗积分饱和处理对基础PID 控制进行改进，最终达到探测器温度的控制要求。

本文介绍了FY-3 紫外临边光谱仪探测器温度控制系统的组成、工作原理和实现方法。通过多次大型整机环境实验验证该系统性能。结果表明：本系统可实现对FY-3 紫外临边光谱仪CMOS探测器温度的精确控制，探测器目标温度可以灵活更改，并且在指定控制参数下，可以使探测器温度变化速率和控温精度均满足控制要求。

2 温度控制系统的构成及其工作原理

FY-3 紫外临边光谱仪的安装位置是舱内，在轨运行时，仪器的环境温度是室温。根据探测器的特性和探测需求，需要将CMOS 探测器的工作温度保持在-10 °C，低于环境温度。所以设计的CMOS 探测器的温度控制系统需具备降温功能。而对于探测器工作结束后的回温过程，则可以通过逐渐减弱制冷器的制冷强度，再通过探测器自身与环境的热交换，使探测器温度恢复到环境温度，故CMOS 探测器的温控系统不需要具备升温功能。除此之外，还需要保证探测器的温度不被周围电源模块、汞灯、钨灯等其他辐射源干扰。

2.1 CMOS 温度控制系统的构成

图1 为温度控制系统结构图。本温控系统由温度采集单元、算法控制单元、功率控制单元、半导体制冷器、CMOS 探测器组成。

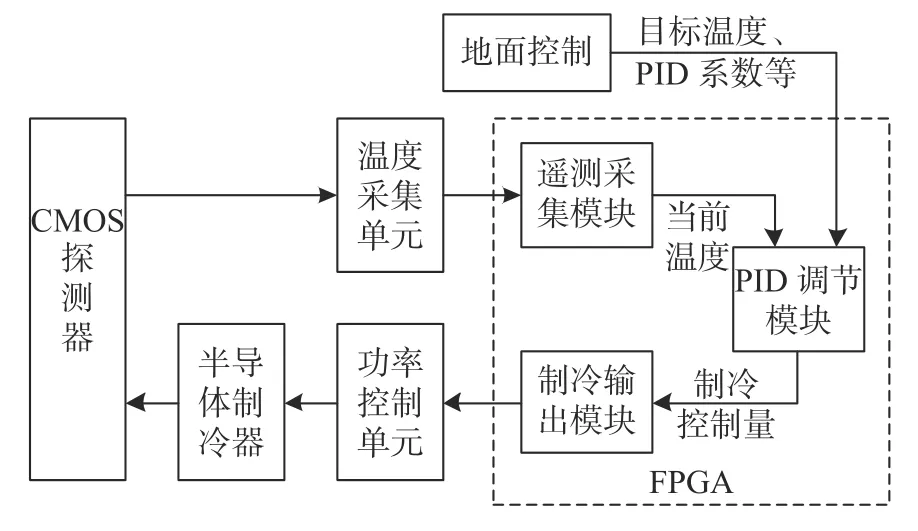
图1 温度控制系统结构图Fig.1 Block diagram of temperature control system

探测器内置MF501 测温热敏电阻。温度采集单元由多路选择器、运算放大器、A/D 转换器组成。功率控制单元由D/A 转换器、运算放大器、场效应管组成。算法控制单元由FPGA 实现，内含遥测采集模块、PID 调节模块、制冷输出等模块。

2.2 温度控制系统的工作原理

系统采用帕尔贴效应对探测器制冷。制冷器与焦平面之间安装了导热块。探测器的温度通过导块传输到焦平面，进而传输到用于整机散热的热管中。

设定遥测采集周期为500 ms，FPGA 控制遥测采集模块每间隔500 ms 驱动一次外部DAC，采集探测器当前温度遥测值。PID 调节单元根据来自地面注入的目标温度、PID 系数，结合当前温度遥测值，利用增量式PID 算法计算出制冷控制增量，控制增量与上次输出的控制量叠加得到当前控制量，然后制冷输出模块驱动外部DAC 将当前控制量输出到功率控制单元，功率控制单元将制冷控制量作用到制冷器上，实现对探测器制冷。

周期地循环上述过程，即可实现对探测器温度的动态调节。合适的制冷电流变化规律可以使探测器以指定的温变速率变化到目标温度，并且以一定精度稳定在目标温度。本系统中，FPGA输出的制冷控制量越大，制冷电流越大，系统制冷强度越强。制冷控制量与制冷强度正相关。

3 温度控制系统的关键算法

3.1 PID 算法

PID 控制原理图如图2 所示。PID 算法由比例项（Proportion）、积分项（Integral）、微分项（Differential）组成。设目标值为r(t)，实测值为y(t)，PID 控制算法的输入为目标值与实测值的偏差e(t)，输出为u(t)。PID 算法对一段时间以来的偏差e(t)进行比例、积分、微分计算，得到控制值u(t)，将控制值u(t)作用到被控对象，即可实现对被控对象的控制[10]。

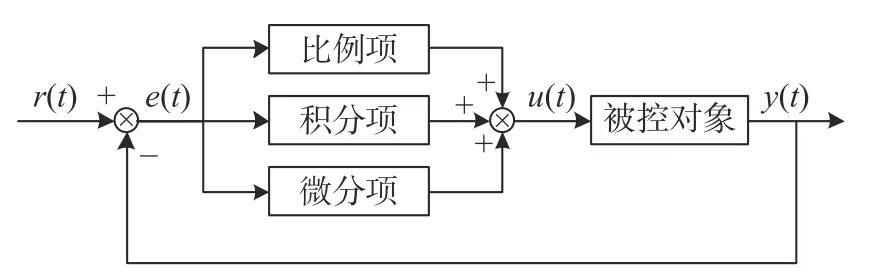
图2 PID 控制原理图Fig.2 Schematic diagram of PID control

设比例项系数为Kp，积分时间常数为Ti，微分时间常数为Td，PID 控制算法在连续系统中的公式为：

由式(1)可知，当温度偏差存在时，比例项将针对当前偏差立即起到减小偏差的作用；积分项是针对过去所有的偏差，起到消除系统偏差的作用；微分项是根据偏差的变化规律提前阻止即将发生的变化。对于这种结合现在、过去、将来的控制，理论上，如果系数合适，即可实现对被控对象的动态校正。

3.2 数字PID 算法

由于数字控制是一种离散采样的过程，需要将模拟PID 控制算法离散转化成数字PID 算法后，才能应用于数字控制中。数字PID 算法有两种：位置式PID 算法和增量式PID 算法。

3.2.1 位置式PID 算法

位置式PID 算法是由模拟PID 算法离散化后直接得到的。设采样间隔为T，采样序号为k，模拟PID 算法离散化后，即得到位置式PID 算法表达式：

其中，Ki是积分项系数，Kd是微分项系数。

3.2.2 增量式PID 算法

增量式PID 算法是由位置式PID 算法变形而来，它的输出为控制量的增量 Δuk。增量式PID 算法与位置式PID 算法的关系为：

将式(2)位置式PID 算法的表达式带入式(3)，得到增量式PID 算法表达式：

对比式(2)和式(4)可以看出，位置式PID 算法需要对历次的偏移量进行累加和计算，而增量式PID 算法只需要计算最近三次的偏移量。二者相比较，增量式PID 算法的计算量更小、稳定性更强，更适用于基于FPGA 的数字控制系统。

由于本系统内的功率控制单元不具备记忆能力，不能接收控制增量只能接收控制量，所以选择用FPGA 储存上次的控制量，利用式(3)，将上次的控制量与本次计算的控制增量相加，得到本次控制量，最终将本次控制量输出到功率控制单元实现控制。

3.3 算法的改进

3.3.1 目标值过渡过程

PID 算法是一种快速调整偏差的算法，如果实测值与目标值的偏差很大，为了快速校正偏差，会产生较大的控制量。在本系统中，当系统刚启动或探测器目标温度改变时，制冷目标温度与探测器当前温度可能会相差较大。这种情况下，为了使探测器温度达到目标温度，PID 控制会连续产生最大制冷电流，使探测器温度快速下降。但是由于背照式CMOS 探测器的工艺特性，温度冲击可能会对探测器造成不可逆的损坏。为了提高系统稳定性，延长探测器寿命，要求探测器的温度按照4 °C/min～5 °C/min 的速度变化。

考虑到探测器要求的温变速率区间较小，但是探测器温度对制冷电流的响应很快，设计时在PID 算法的前端增加了一个过渡过程控制。使输入到PID 算法的探测器目标温度按照要求的温变速率缓慢变化。

已知要求的变化速率为4 °C/min～5 °C/min，那么将4.5 °C/min 作为目标温度过渡过程的变化速率v。为了便于调试，将时间步长n与温度增量ΔT均设计为界面可输入的参数。则有，

由于系统采样间隔是500 ms，所以时间步长的单位是500 ms。这个过渡过程可使每间隔n个500 ms，输入到PID 控制器的目标温度增加或减少 ΔT。通过多次单机、整机、整星大型环境实验可以证明，当设置n=8，ΔT=0.3 °C 时，在回温和制冷的过程中，均可使探测器温度变化速度达到要求的4 °C/min～5 °C/min。

3.3.2 抗积分饱和控制

PID 调节单元输出的制冷控制量是通过外部DAC 作用到制冷器的。真正作用到制冷器的控制量的范围受DAC 的量化位数限制。本系统中使用的DAC 是12 位量化，那么，实际可输出的控制量的码值范围是000H 至FFFH。

本系统有制冷功能没有加热功能。控制探测器制冷是增大控制量的过程；控制探测器回温是减小控制量的过程。PID 调节单元输出到DAC的控制量越大，那么制冷电流越大，系统的制冷强度越强。当控制量为FFFH 时，制冷电流达到最高，值为1.1 A。反之，PID 调节单元输出到DAC的控制量越小，那么制冷电流越小，系统的制冷强度越弱，当控制量为000H 时，制冷电流达到最小，值为0 A。此时制冷电路的开关状态不变，只是不起制冷作用。

当PID 算法得到的控制量低于极限小值000H，或高于极限大值FFFH 时，如果不对输出做限幅处理而直接截断输出，那么实际制冷作用可能会与预期相差较大，甚至相悖。这种情况将会导致制冷时间过长，甚至出现震荡而无法制冷，达到目标温度。

这种现象是由积分饱和导致的，解决的办法是对PID 调节单元的输出做限幅处理，即，当PID 算法得到的控制量超过FFFH，那么PID 调节单元将输出最大边界值FFFH，并且取消积分作用，即将积分项系数置0；当PID 算法得到的控制量是负值，那么PID 调节单元将输出最小边界值000H，并且取消积分作用，即将积分项系数置0。只有当控制量在000H 至FFFH 范围时，才执行积分运算，并输出控制量。

4 温度控制系统的实现

4.1 数字PID 算法

由图3 探测器温度码值曲线可知，探测器的温度越低，对应的码值越大；在本系统中，输出控制量越大，制冷效果越强。在本系统中，偏差为目标值减去实测值，即：

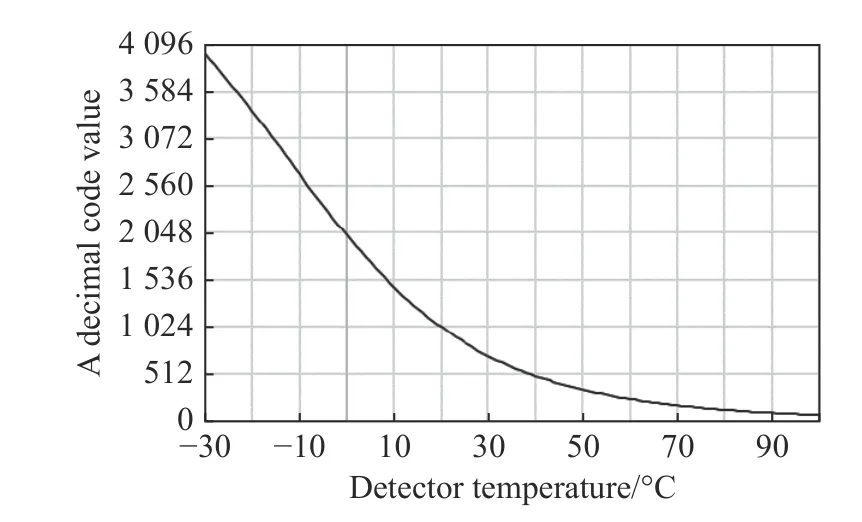
图3 探测器温度和码值关系曲线Fig.3 Relationship between detector temperature and code values

即，当制冷目标温度大于当前温度时，温度偏差的符号为正，否则为负。

图4 为此温度控制系统的软件实现流程。按照系统要求，遥测采样的间隔为500 ms。在温控流程中，每个遥测采样时刻均为一次温度调节的开始时刻。此温控系统的实现流程为：

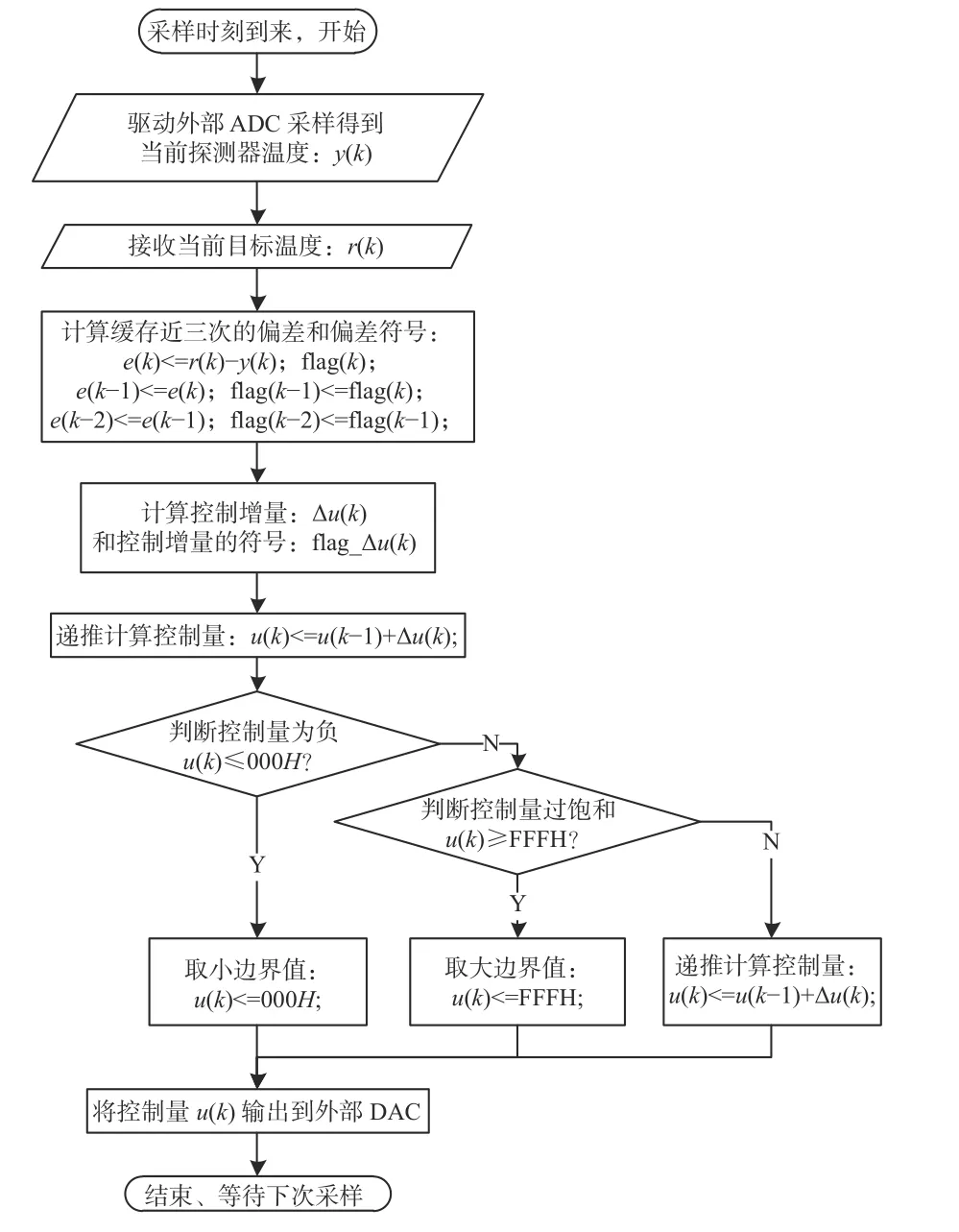
图4 温度控制系统的软件流程图Fig.4 Flow chart of temperature control system software

当采样时刻到来时，首先，从遥测采集模块读取探测器当前温度遥测值，同时读取经过前置滤波器的当前目标温度 ；

接着，计算当前温度遥测与目标温度值的偏差，并标记偏差的符号，同时缓存前两次的温度偏差和偏差的符号；

然后，将最近三次的偏差和偏差符号带入增量式PID 算法，计算控制增量并标记控制增量的符号；

利用式(3)，将控制增量与上一次的控制量叠加，得到当前控制量；

再对当前控制量做限幅处理，得到最终要输出的控制量；

最后，驱动外部DAC 将限幅后的控制量输出到功率控制单元，进而作用到制冷器。此时一次温度调节结束，等待下一次采样时刻到来，重复上面过程，开展新一次温度调节。

4.2 PID 参数整定

PID 控制算法由比例项、积分项、微分项组成，每一项的系数决定了该项作用的强弱。

比例项的作用是快速修正偏差，比例项系数越大，效果越强，但如果比例项系数过大，将会产生较大超调；积分项的作用是补偿系统的静差，积分时间常数越小，积分项作用越强，消除系统静差的时间越短，但如果积分项作用过强，将会引起振荡；微分项的作用是提前阻止偏差的变化，在偏差变化之前进行修正，适用于噪声较小的系统，微分时间常数越大，微分项作用越强，合适的微分项系数可以加快修正速度，提高系统稳定性。

PID 参数整定方法有临界比例法、反应曲线法、衰减法和经验法。本系统采用经验凑试法，通过多次试验，根据实际控制情况，按照比例系数、积分系数、差分系数的顺序调整，最终选择合适的PID 系数。

5 测量实验与结果

经过多次整机温度循环、老炼等环境实验发现，FY-3 紫外临边光谱仪探测器温控系统制冷或回温的温度变化速率均可通过数据注入灵活调节，目标温度也可通过数据注入灵活控制。该系统可在指定参数下满足探测器温度的控制要求。

系统要求探测器制冷和回温的速率均满足4 °C/min～5 °C/min。在多次环境实验中，随机提取一次制冷过程曲线如图5（彩图见期刊电子版）所示，一次回温过程曲线如图6（彩图见期刊电子版）所示。

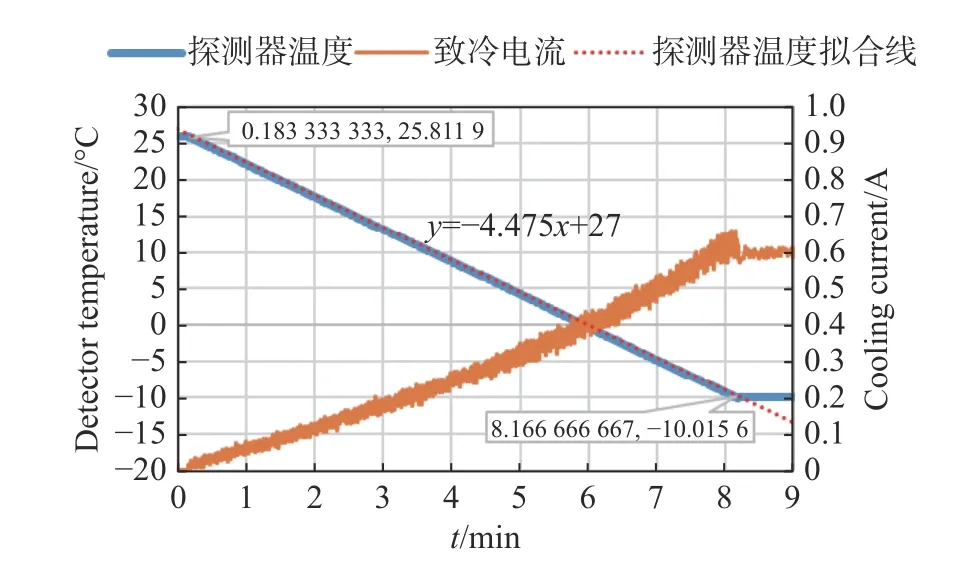
图5 制冷过程曲线Fig.5 Temperature cooling curve of the detector

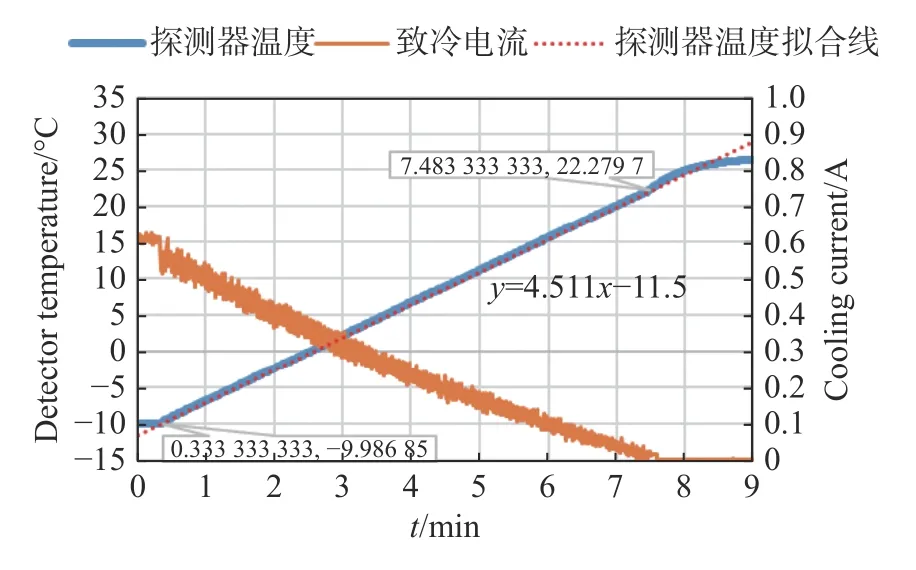
图6 回温过程曲线Fig.6 Temperature rising curve of the detector

由图5 制冷过程曲线可以看出，随着制冷电流的增大，探测器温度在降低。由图6 回温过程曲线可看出，随着制冷电流减小，探测器温度在升高。制冷电流在变化过程中有微小的调整，使得探测器温度基本呈线性变化。将图5 和图6 中探测器温度曲线在温度变化阶段进行拟合。可以看出，探测器温度的变化速率控制在了(4.5±0.05) °C/min内，满足指标范围要求。

探测器制冷目标温度默认为-10 °C，但也可根据实验情况随时调整，如图7 和图8 分别为制冷目标温度为-5 °C 和-10 °C 时，在一个轨道时间内持续工作过程中，探测器温度散点图。可见，目标温度分别为-5 °C 和-10 °C 时，控制误差均可以达到±0.1 °C，优于指标±0.2 °C。

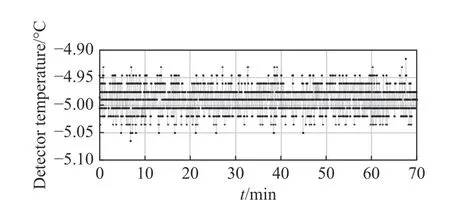
图7 目标温度为-5 °C 时的温度散点图Fig.7 Scatter plot of temperature at a target temperature of-5 °C

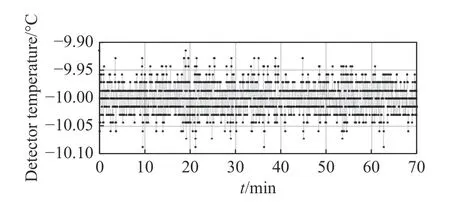
图8 目标温度为-10 °C 时的温度散点图Fig.8 Scatter plot of temperature at a target temperature of-10 °C

FY-3 紫外临边光谱仪使用的探测器有效感光区域为2 000×100，光谱维覆盖2 000 行，空间维覆盖100 列。在轨运行时，对有效感光图像的光谱维2 000 行不合并，空间维100 个像元合并后再下传。

使用钨灯作为标准光源，积分时间设置为12 s，分别在室温23 °C 条件和制冷到-10 °C 条件下拍摄100 帧，曲线对比情况如图9（彩图见期刊电子版）所示。图9 横坐标为有效感光区域的光谱维行序号1～2 000；纵坐标为有效感光区域的空间维100 个像元合并后的DN 值。

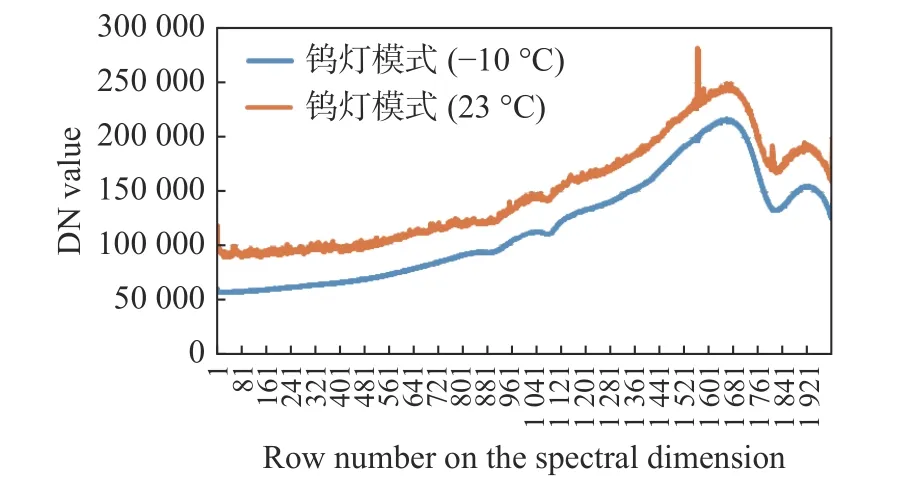
图9 不同温度的钨灯曲线图Fig.9 Temperature curves of different tungsten lamps

由图9 可看出，常温下，曲线有两处尖峰，这是由探测器上的坏点造成的，它们对于光响应与其他正常像素的反应不同。通过使探测器降温，异常像素的光响应将恢复正常，曲线的异常尖峰值也将消失。并且，温度的降低使得探测器的暗电流降低，光谱曲线向下平移，并且噪声减小，光谱曲线更加平滑。取对应像元在100 帧内的平均值作为信号值，标准差作为噪声，信号值除以噪声可得到信噪比。绘制信噪比曲线如图10 所示。可见，信噪比在探测器温度为-10 °C 时比温度为23 °C 时有所提高。

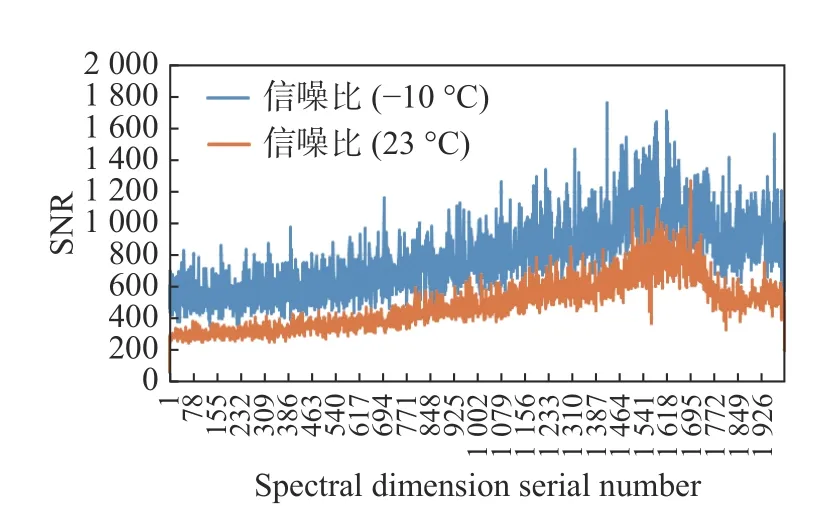
图10 不同温度的信噪比曲线Fig.10 SNR curves at different temperatures

将入光口遮住，使探测器置于暗场环境，积分时间设置为12 s，分别在室温23 °C 条件和制冷到-10 °C 条件下拍摄100 帧图像。剔除上述两处尖峰位置的异常点，计算对应像元在100 帧的标准差，作为暗噪声，绘制曲线如图11 所示。可见，在制冷的作用下，探测器暗噪声得到了有效抑制。

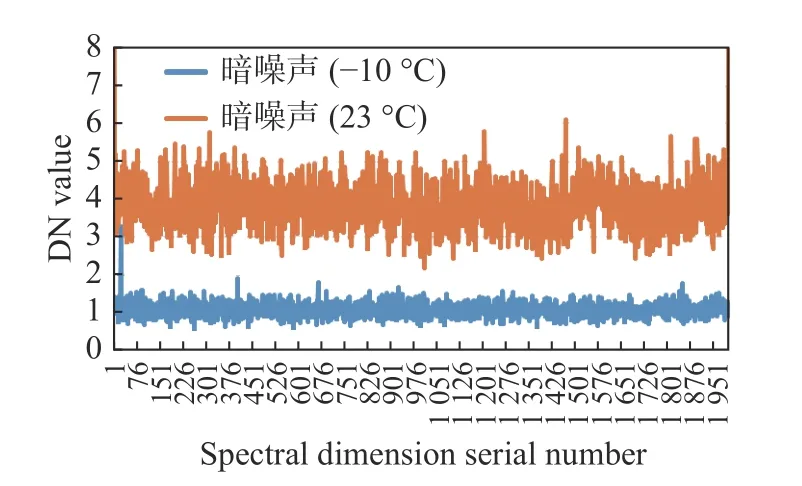
图11 不同温度的暗噪声曲线Fig.11 Dark noise curves at different temperatures

6 结论

本文介绍了一种FY-3 紫外临边光谱仪探测器的温度控制系统。通过对比实验看出，低温条件下，FY-3 紫外临边光谱仪探测器的噪声得到了有效抑制。通过多次大型整机环境实验可以证明，此温控系统的目标温度和温变速率均可通过数据注入灵活调节。在指定参数下，制冷速率和回温速率均可以控制在(4.5±0.05) °C/min，满足4 °C/min～5 °C/min 的指标要求。在不同目标温度下，控温精度均可达到±0.1 °C，优于指标要求。本文所设计的探测器温度控制系统具有灵活度高，控温精度高，抗干扰能力强的特点。