动态工况下基于WOA-BiGRU的PEMFC性能退化预测

杨 柳,王 巍

(1.湖北开放大学 机电工程学院, 武汉 430074;2.中南财经政法大学 信息与安全工程学院, 武汉 430074)

0 引言

质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)在现代可持续清洁能源系统中发挥着关键作用[1-2]。PEMFC是一种轻量化、功率密度高的清洁发电装置,因此在军事、交通等领域得到广泛应用。然而PEMFC的老化现象和寿命问题限制了其进一步商业化和大规模应用[3-4]。

现有的PEMFC预测方法主要分为模型驱动方法和数据驱动方法[5]。模型驱动方法可以反映PEMFC老化涉及的物理和化学过程[6]。Zhou等[7]基于电化学反应原理建立了一种多物理老化模型,通过考虑欧姆效应、活化损耗和反应物传质损失来预测PEMFC的性能退化。Moein-Jahromi等[8]和Futter等[9]从组件层面考虑了PEMFC的老化,分别解释了催化剂层和质子交换膜的老化原理。Liu等[10]提出了一种基于模式识别的方法,使用经验模型从极化曲线中提取静态特征,然后利用专家知识和参数建模从电化学阻抗谱中提取动态特征。

模型驱动方法中的一些参数通常被假设为常数以简化建模过程。但PEMFC老化机制尚未研究透彻,各种老化模型通常未经证明,模型驱动方法的预测准确性通常无法保证。因此,研究人员提出了数据驱动方法。

数据驱动方法基于充足的寿命数据预测PEMFC的老化过程和剩余使用寿命,无需考虑其老化原理。主流的数据驱动方法主要基于神经网络,Liu等[11]提出了一种循环神经网络方法(recurrent neural network,RNN),采用规则间隔采样和局部加权散点平滑来实现数据平滑与重构,在反向传播神经网络的基础上,使用长短期记忆方法(long short term memory,LSTM)将预测精度提高了28.46%。Long等[12]使用与Liu等类似的处理步骤进一步证明门控循环单元(gated recurrent unit,GRU)优于LSTM。Hua等[13]使用基于RNN的回声状态网络(echo state network,ESN)进行预测,使用反映神经元动态的随机生成库替换ESN中的隐藏层,以提高预测效果。

数据驱动方法属于黑盒模型,缺少对PEMFC多样性老化因素的考虑。Ma等[14]的研究表明,燃料电池内部电化学反应会改变内部温度、气体流量和溶液条件,导致电极、气体扩散层、催化剂层和质子交换膜发生老化,从而导致PEMFC的性能出现退化。因此,提出的各种预测模型应当能够充分适应并反映其退化趋势。此外,现有方法缺少对电压恢复现象的考虑。Chu等[15]对3个燃料电池堆分别进行了2 500 h的耐久性测试,表明导致燃料电池性能下降的部分组件的老化是可逆的。操作条件的变化可能会导致部分组件和整体PEMFC系统的性能显著恢复,这种性能恢复导致随着运行时间增加,PEMFC的输出电压整体呈下降趋势,但会在局部出现回升,称为电压恢复现象。

综上所述,现有的数据驱动预测方法缺少对老化机制的考虑,同时,PEMFC的复杂工作机制也给模型驱动方法的使用带来了挑战。在动态工况下,PEMFC频繁启停导致的性能退化和电压恢复现象更加明显。

因此,提出一种双向门控循环单元方法(bi-directional gated recurrent units,BiGRU),并使用鲸鱼优化算法(whale optimization algorithm,WOA)优化BiGRU网络的超参数,以应对PEMFC性能退化和电压恢复现象。以PEMFC电压作为反映整体性能的指标,在动态工况下进行验证,通过与现有方法的对比,证明了WOA-BiGRU方法的优势。

1 实验数据分析

1.1 参数设置与电流等级划分

使用提出的方法对动态工况的实验结果进行研究,该实验包含3 076次动态负载循环过程,共计1 008 h。单次循环内的电压变化如图1所示,关键参数设置见表1。每隔50 h关闭1次以测量PEMFC内部物理状态,关闭到再次开启期间,PEMFC工作状态发生显著变化,导致组件性能恢复。

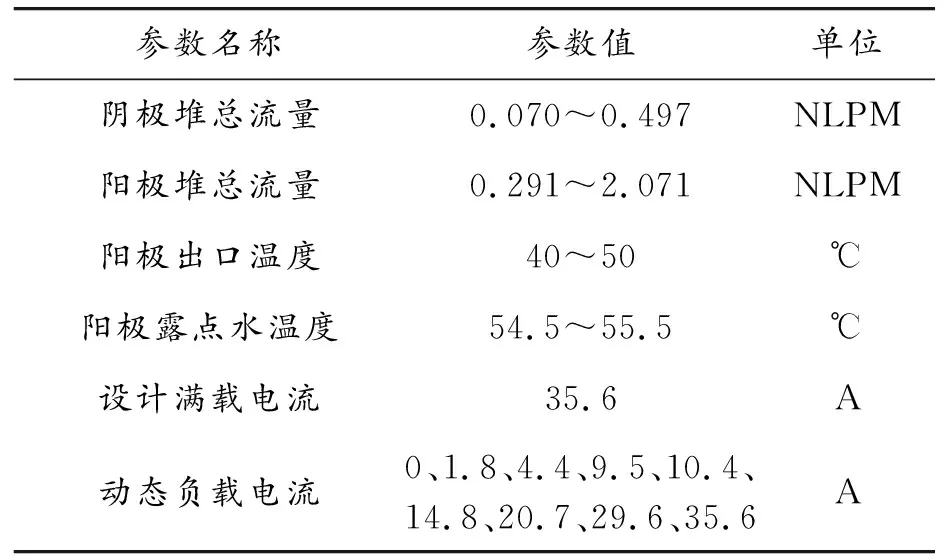
表1 关键工作参数(部分)

图1 单次循环电压变化

实验负载电流分为9个等级,使用10.4 A负载电流下的电压数据表征PEMFC性能,以1 h为间隔取用前1 000 h电压数据,如图2所示。动态工况下的电压恢复现象使燃料电池的老化机制变得复杂,预测也更加困难。而提出的WOA-BiGRU数据驱动方法可以获得更好的模型参数,很好地适用这种情况。

图2 10.4 A负载电流下电压变化

2 模型建立

2.1 预测方法框架

WOA-BiGRU方法的预测原理如图3所示。

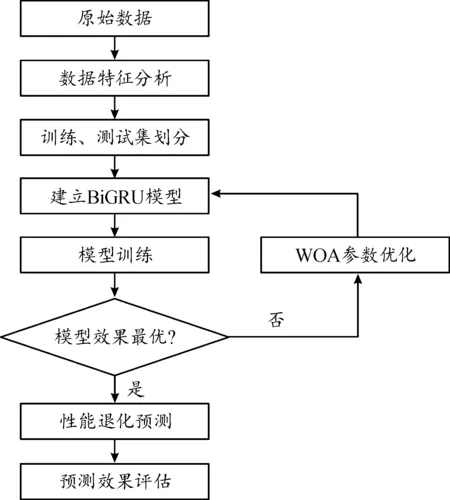
图3 预测方法框架

在提出的混合预测模型中,首先使用随机森林算法进行数据特征分析,确定模型训练使用的特征量。然后建立BiGRU模型,并使用WOA算法进行参数优化。最后,使用经过优化的BiGRU模型进行PEMFC性能退化预测,并进行预测效果评估。下文对模型的建立过程展开说明。

2.2 随机森林

使用随机森林进行数据特征分析,以明确各个变量的重要程度。随机森林具有处理高维数据和快速训练的能力。因此,选择它作为对原始数据进行预处理的方法。主要步骤如下:

1) 以基尼系数(Gini coefficient,GI)和特征重要性(variable importance measure,VIM)作为衡量贡献度的指标。对第m个节点有:

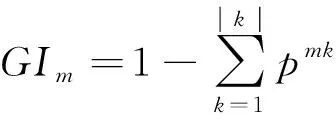
(1)

式中:k表示特征数量,pmk是第k个特征在第m个节点上的分数。则特征Xj在第m个节点的重要性计算为:

VIMjm=GIm-GIl-GIr

(2)

式中:GIl和GIr分别为对应分支前后2个节点的基尼系数。

2) 当特征Xj包含在决策树I的不同节点,设m属于集合M(m∈M),则第i个树的重要性可表示为:

(3)

此时,Xj的特征重要性表示为:

(4)

2.3 BiGRU

BiGRU由正向GRU和反向GRU组成,单个GRU的结构如图4所示。

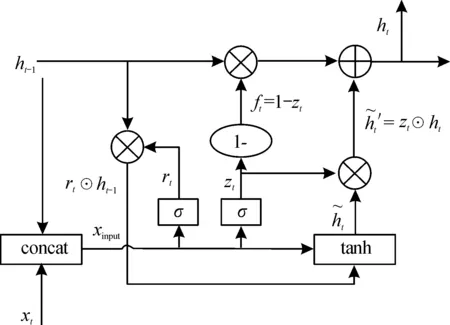
图4 GRU结构

各环节计算原理为:

zt=σ(Wz·[ht-1,xt])

(5)

rt=σ(Wr·[ht-1,xt])

(6)

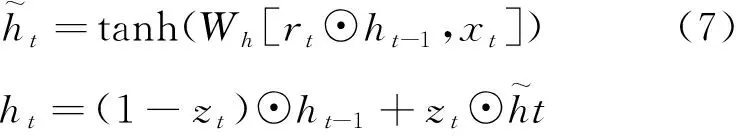
(8)

式中:Wz、Wr和Wh分别是更新门、重置门和候选状态的网络权重,σ、tanh均为激活函数。

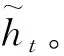
BiGRU的隐藏状态由正、反2个GRU的状态共同决定,如图5所示。此时,BiGRU隐藏状态的生成过程可表示为:

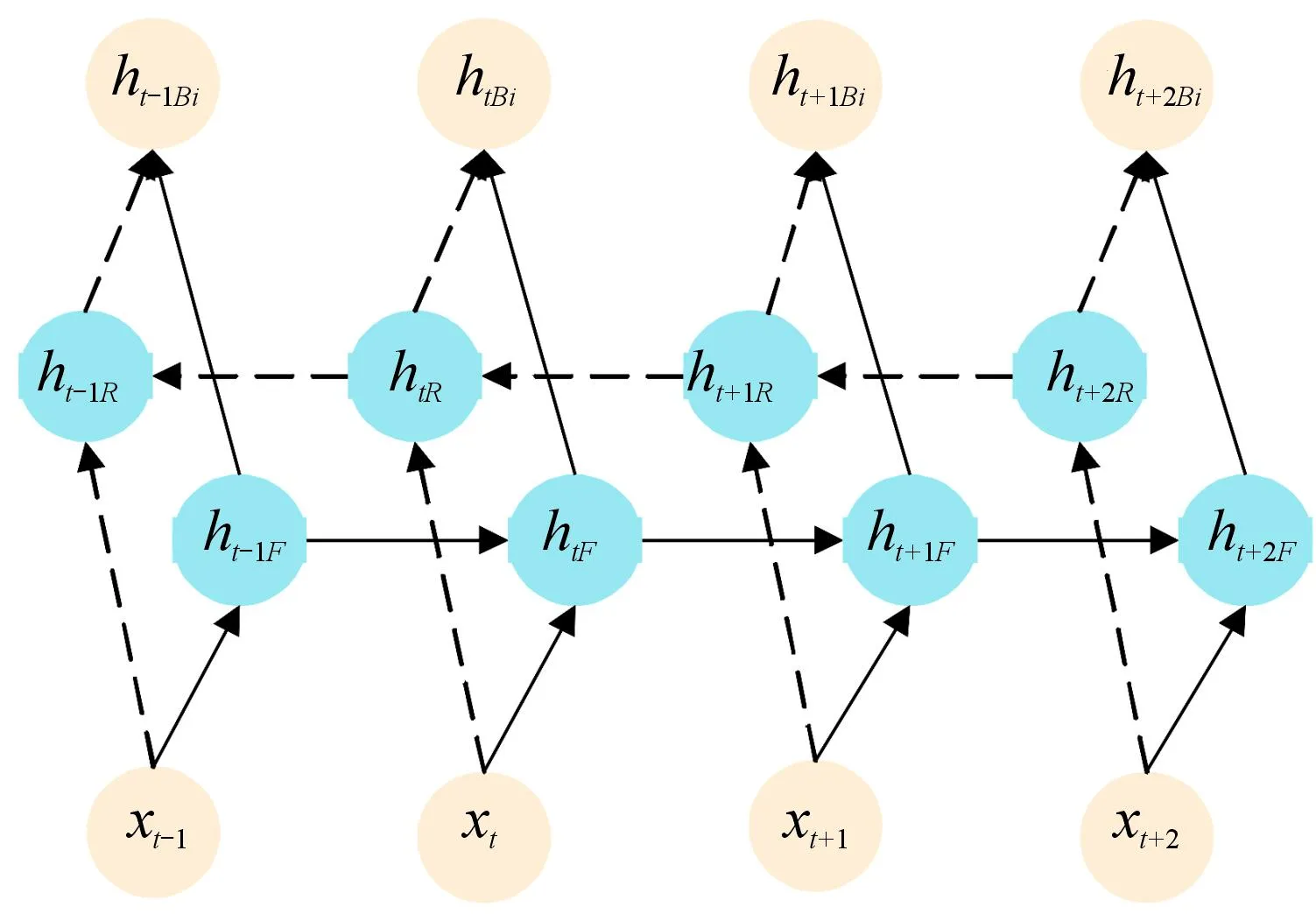
图5 BiGRU结构

htBi=Bi(htF,htR)

(9)

式中:htBi为BiGRU在当前时刻的隐藏状态,htF和htR分别表示正向和反向GRU的隐藏状态。这种双向结构使BiGRU可以更好地提取电压变化特征,提高对电压变化的预测效果。

2.4 WOA算法

使用WOA算法获取最佳的BiGRU模型参数。WOA算法是模仿自然界中鲸鱼捕食行为的群体优化算法,包括包围猎物、狩猎行为和搜索猎物3个步骤[16-17]。

X(t+1)=Xp(t)-A·D

(10)

D=|C·Xp(t)-X(t)|

(11)

式中:t为迭代次数,X(t)为鲸鱼个体当前的位置向量,X(t+1)为鲸鱼个体下一迭代内的位置向量,Xp(t)为猎物的位置向量,A和C为系数向量,随迭代次数进行更新。

2) 狩猎行为。在狩猎阶段,WOA算法对包围区域内的潜在解进行搜索,使算法更快地接近最优解,并一定程度上避免陷入局部最优解。其数学模型表示为:

X(t+1)=D·ebl·cosθ+Xp(t)

(12)

式中:常量系数b决定鲸鱼个体螺旋前进时的螺旋线形状,b取值为1时即为普通的对数螺旋线;l∈[-1,1],θ∈[-2π,2π]。同时,利用p(p∈[0,1])判别位置更新采用的方式,其数学模型为:

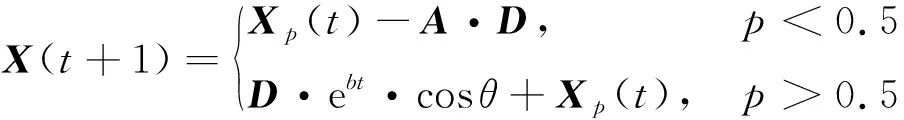
(13)

3) 搜索猎物。WOA算法模拟鲸鱼搜索猎物的行为,使用参数A控制处于搜寻猎物或包围猎物阶段,以通过实现全局搜索策略。当|A|>1时,鲸鱼缺乏猎物有效信息,需要通过随机方式发现猎物线索并进行搜索。该算法的数学模型为:

D=|C·Xrand(t)-X(t)|

(14)

X(t+1)=Xrand(t)-A·D

(15)

式中:Xrand(t)为随机生成的鲸鱼个体位置向量。

3 实验效果分析

3.1 误差指标

采用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)来表征预测效果,相应数学表达式如下:

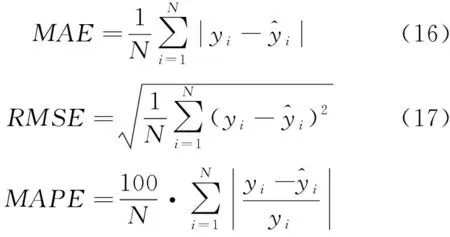
(18)

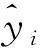
3.2 实验结果分析

3.2.1 特征重要性

使用随机森林算法分析原始数据中的各种信息,对得到的重要性进行归一化,如表2所示。

表2 随机森林特征重要性

使用10.4 A电流条件下的电压数据,可以视为电流恒定,因此功率与电压呈线性关系,这与表2中功率重要性最高的结果相符。此外,表2中显示阴极堆、阳极堆总流量的重要性最高,进口、出口温度的重要性其次,各处压力的重要性最小。

根据表2中特征重要性,选用功率、阴极堆总流量、阳极堆总流量进行模型训练。

3.2.2 WOA-BiGRU预测结果

使用前500 h数据进行训练,后500 h数据进行预测,评估WOA-BiGRU方法的预测效果。得到的预测电压如图6所示,每小时预测值的误差值如图7所示。

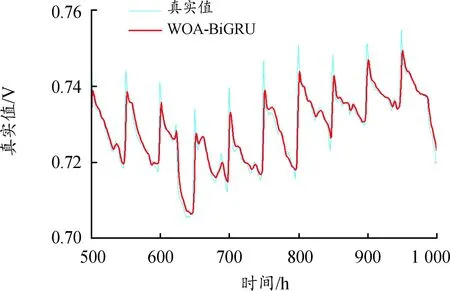
图6 500 h的WOA-BiGRU预测电压曲线

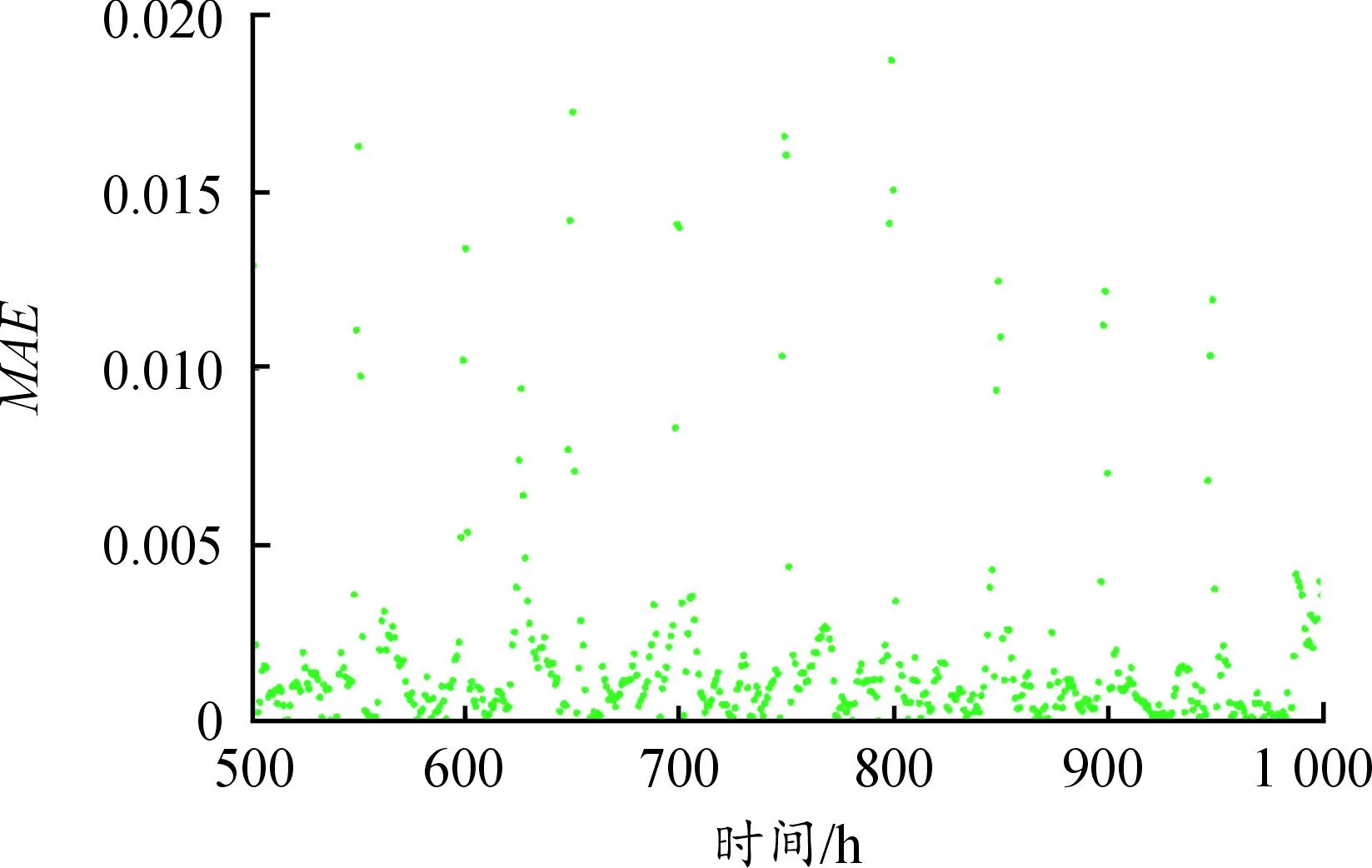
图7 500 h的预测误差值

如图6和表3所示,预测电压和真实电压之间具有良好的相关性,但存在局部预测效果的下降。图6中,波峰波谷处的预测值普遍偏小,表明了电压恢复现象对预测效果的影响。

表3 多训练集比例、多方法误差对比

图7显示,大部分预测误差的数值在0.005以下,表明WOA-BiGRU方法具有较为稳定的预测效果。此外,少部分预测误差在0.005～0.020的范围间波动,这表明局部电压剧烈波动对WOA-BiGRU方法的预测效果影响有限,说明了WOA-BiGRU方法对电压恢复现象的良好适应性能。

4 优越性验证

4.1 双向机制优越性

为验证使用的双向机制的优势,分别使用LSTM、BiLSTM、GRU、BiGRU方法进行验证。与前文相同,使用前500 h数据进行训练,后500 h数据用于验证。预测结果如图8所示,相应的预测误差见表3。

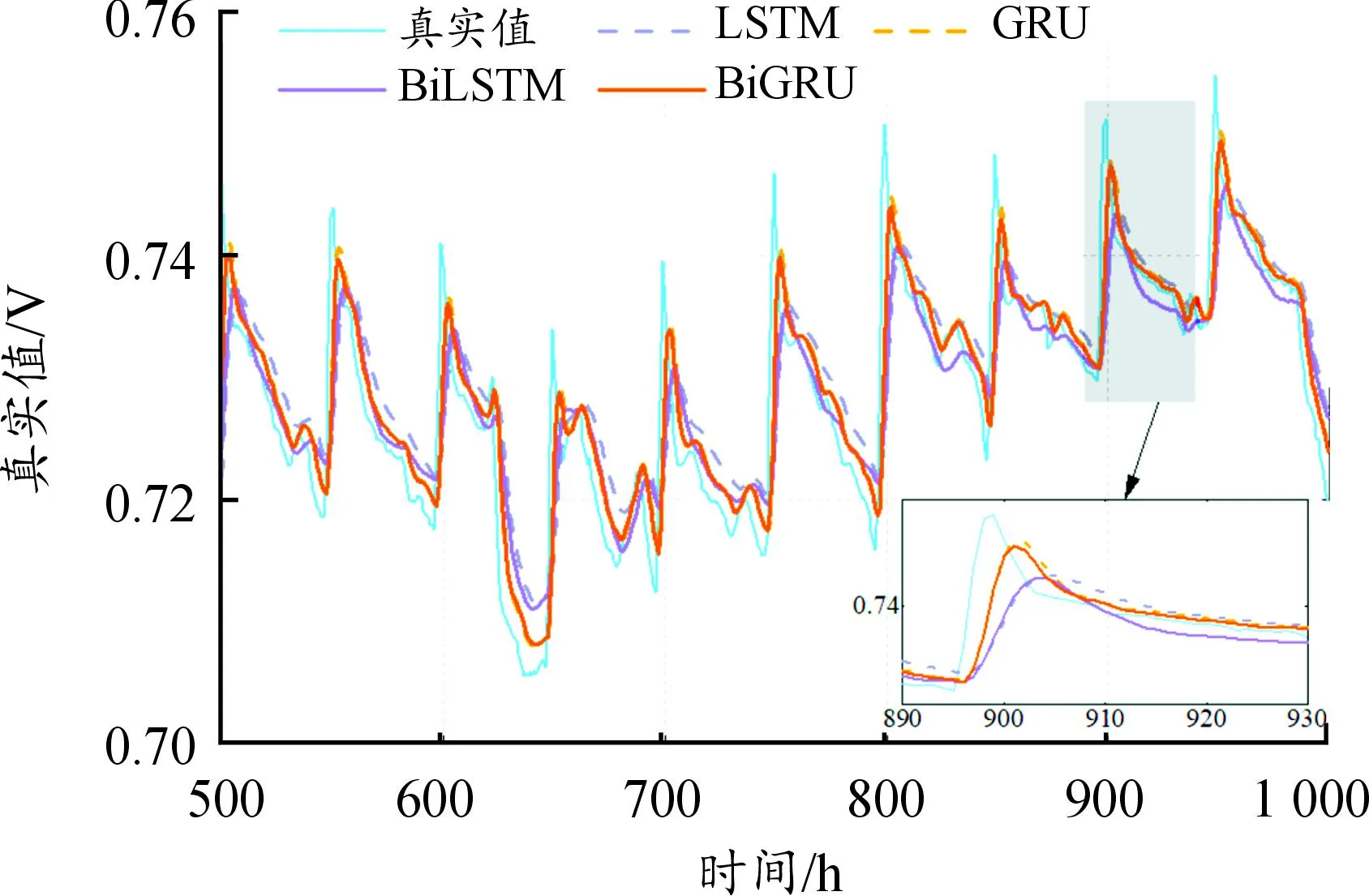
图8 500 h双向机制优势验证

由图8中可以看出,4种方法都可以实现预测目的,但整体预测性能存在差异。对比BiLSTM和LSTM,可得BiLSTM的预测值普遍更小,而且在650～800 h区间内最为明显,这表明引入双向机制有效提高了LSTM的预测性能。根据图8和表3中500 h下的预测误差,这种引入双向机制的优势对GRU仍然成立。

由图8可得,在波峰、波谷处,BiGRU的预测性能比BiLSTM更好,这一现象在650 h处波谷、700 h波峰处表现最为明显。因此选用BiGRU结合WOA算法,通过优化BiGRU的参数以进一步提高预测效果。

4.2 WOA参数优化

为验证WOA算法的作用,分别使用BiGRU、WOA-BiGRU进行验证。训练、测试集设置与上文相同。得到的预测结果如图9所示,相应的预测误差见表3。

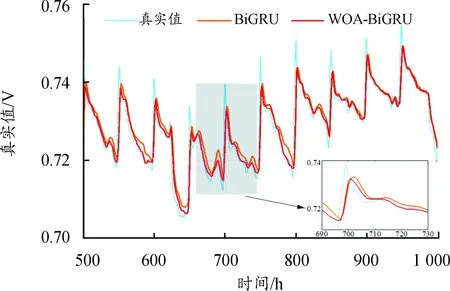
图9 WOA算法优势验证

由图9可以看出,2种方法都可以实现预测目的,但WOA-BiGRU对波谷的预测性能更好,这一优势在650 h处的波谷表现最为明显。此外,根据图9中的放大图,在698～705 h的电压上升阶段,2种方法的预测效果相同,而在690～698 h、705～730 h的下降阶段,WOA-BiGRU的预测值更接近真实值。这表明在电压恢复阶段,2种方法的预测性能接近,在其他时间,WOA-BiGRU的预测效果更好。这表明使用WOA算法调整BiGRU参数可以实现更好的预测性能。

4.3 不同训练集比例下预测结果对比

使用多种训练集、多种方法进行对比研究,以验证WOA-BiGRU算法在不同训练集条件下的预测稳定性。得到的预测误差如表3所示,相应的变化趋势如图10—图12所示。使用的算法参数如表4所示。

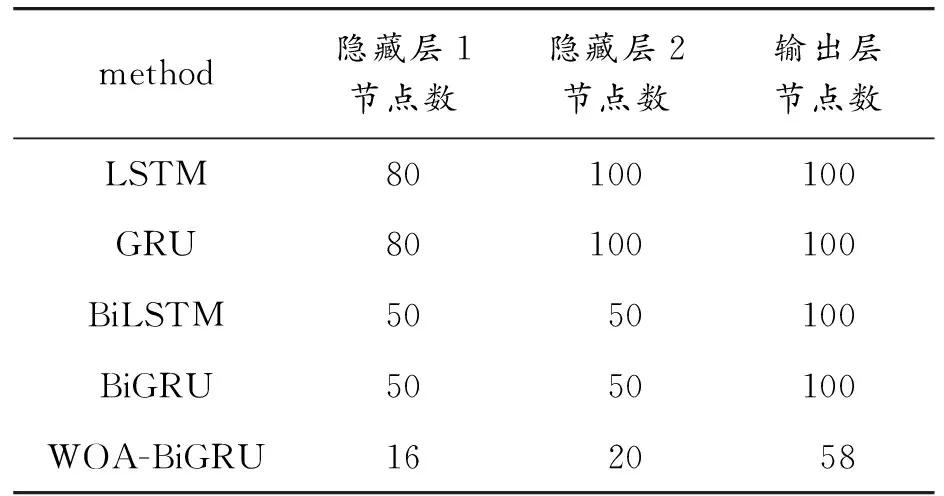
表4 算法参数设置

图10 MAE对比

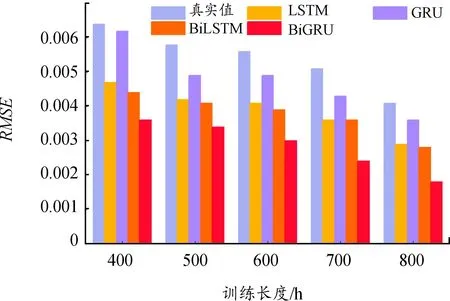
图11 RMSE对比

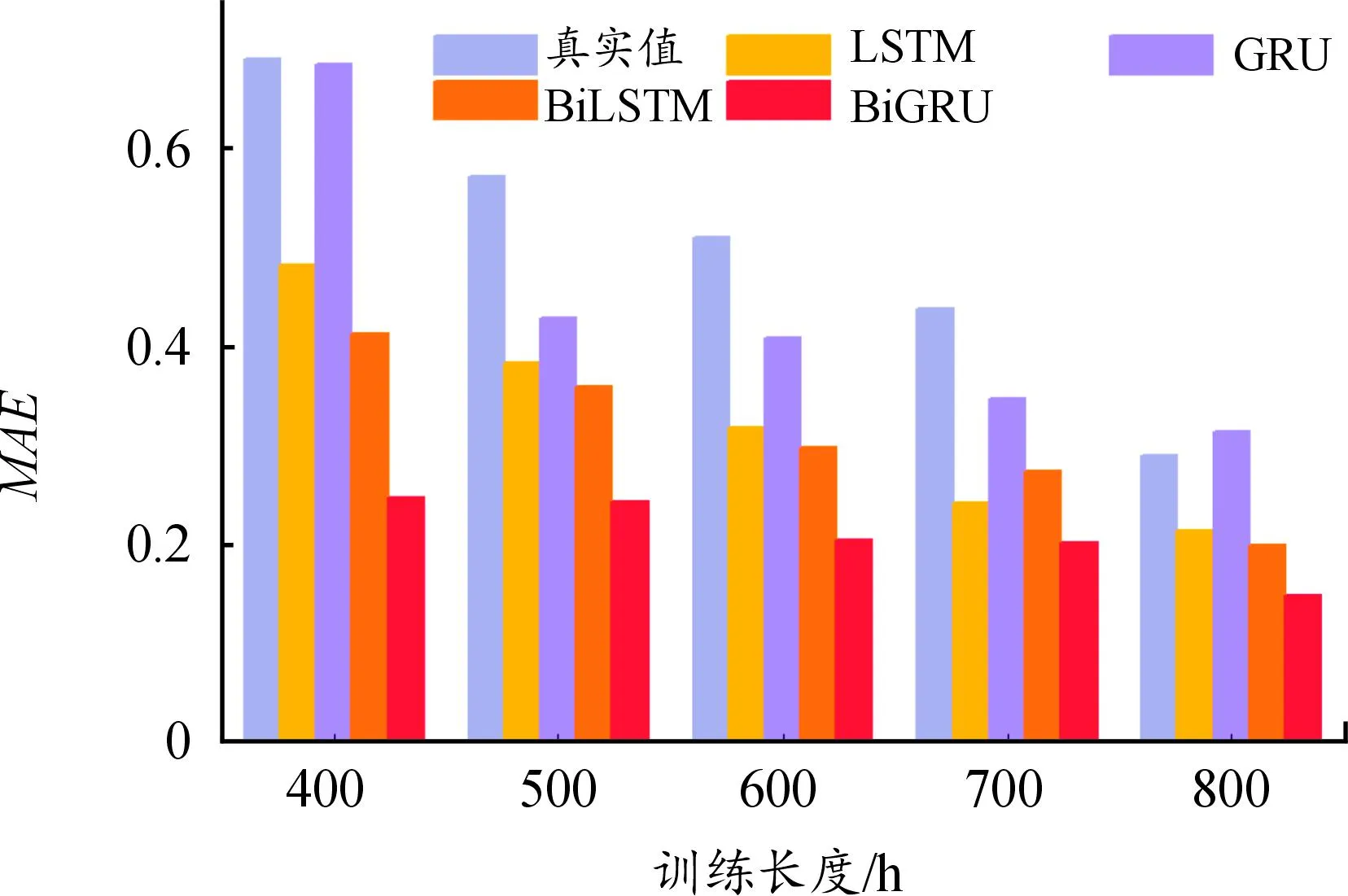
图12 MAPE对比

对比LSTM,BiLSTM的效果提升了10.9%～11.8%。对比GRU,BiGRU的效果提升了3.4%～4.2%。2项对比证明了在多个训练条件下,引入双向机制的优势。而BiGRU比BiLSTM的效果更佳,因此使用WOA算法进一步提高其预测效果。

WOA-BiGRU的效果较BiGRU提高了25.5%～31.2%,较GRU提高了28.1%～33.7%。这表明结合双向机制与WOA优化算法,可以有效提高对PEMFC性能退化的预测能力。

5 结论

1) 使用随机森林进行特征重要性计算,提取3种与电压退化强相关的运行信息进行模型训练。在GRU中引入双向机制,更好地提取数据的变化特征。

2) 使用WOA算法优化BiGRU的模型参数,提高预测模型对电压变化的适应能力,增强预测效果。在500 h训练长度下,将MAE减小到0.001 8,RMSE减小到0.003 4。

3) 结合WOA和BiGRU方法,对比单独GRU方法,更好地适应PEMFC退化过程中的电压恢复现象,将预测效果提高了28.1%～33.7%。

提出的方法可以有效完成PEMFC性能退化预测工作,未来应考虑将该方法扩展到长期预测领域,进一步应用于剩余使用寿命预测。