波浪作用下临海基坑非等长双排钢板桩受力性状研究
2024-02-03罗战友奚灵智俞建强莫修栋
罗战友,李 博,奚灵智,俞建强,莫修栋
(1.宁波大学 岩石力学研究所,浙江 宁波 315211;2.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122;3.宁波市轨道交通建设分公司,浙江 宁波 315000)
双排桩支护结构布桩形式灵活,具有较好的空间刚度,能适应复杂荷载状况,有效控制基坑变形,极大地降低基坑施工对地下空间及周边环境的影响[1-2],在工程中得到广泛应用.诸多研究表明,双排桩结构的内力变形规律受其布置形式、所处地层及荷载条件的影响,存在较大差异.
Phillip 等[3]、Ricardo[4]及Ilyas[5]分析了水平荷载作用下双排桩结构的内力变形特征,发现在适当的范围内增加排距能减小桩体的侧向位移变形.刘钊[6]基于Winkler 弹性地基假设,提出考虑桩土相互作用的双排桩计算模型.何颐华等[7]通过室内试验及工程实测,分析了双排桩的内力、变形及土压力分布特征,提出比例系数法对结构所受土压力进行分配,建立了双排桩平面刚架计算模型.郑刚等[8]对已有双排桩计算模型进行分析,提出了一种可考虑排桩间土层分布变化、压缩性、桩间土加固等影响因素的平面杆系有限元双排桩计算模型.曹俊坚等[9]考虑圈梁对桩空间作用的影响,根据变形协调原理,推导出一种新的双排桩支护计算方法.熊巨华[10]针对排间距小于四倍桩径的双排桩结构,提出一种等效抗弯刚度计算方法,建立了可利用弹性支点法分析的双排桩计算模型.《建筑基坑支护技术规程》[11](以下简称规范)基于大量试验及工程数据,综合多种计算模型,规定出适用范围更为广泛的等长双排桩结构的计算模型.上述研究主要针对常规荷载环境下非连续布置的等长双排桩结构进行分析,当荷载环境及结构布置形式发生变化时,此类计算模型的适用性难以考究.
临海或海上基坑工程受到风、浪等作用,受荷状况十分复杂,地下水位存在较大波动[12].为减小由于风浪作用引起结构产生的振动,避免沉降过大导致结构失稳以及海洋环境下基坑渗流破坏[13],提高工程经济性与效率,部分临海基坑采用非等长双排钢板桩进行支护.
石钰锋等[14]假定围堰芯填土不可压缩,提出一种软土地层双排桩围堰水平位移简化计算方法,结合实测数据及有限元模拟结果对比验证,发现该简化计算方法具有较好的合理性及适用性.罗毅等[15]基于深圳某海底隧道工程建立数值有限元模型,研究了海域双排钢板桩围堰与明挖基坑变形特性及相互影响的规律,发现基坑内支撑形式对钢板桩围堰变形有较大影响,而基坑开挖步序对钢板桩围堰变形影响较小.张逸帆等[16]以澳门某取水口基坑围护结构为例,通过理论计算及数值模拟,分析了有无动水条件下双排桩结构的内力变形特征,发现波浪作用对双排桩的变形影响主要集中在坑底以上部位.张玉成等[17]综述了几种双排桩计算方法,简化了双排桩土压力计算方法,建立有限元双排钢板桩围堰的计算模型,对其位移及变形进行分析,对比现场监测结果发现该计算模型偏安全.侯永茂等[18]对某船坞工程中的大跨度等长双排钢板桩围堰进行现场监测,发现其变形较大,有显著三维空间效应,且前、后排钢板桩变形特性存在差异.朱艳等[19]利用贝叶斯方法将工程经验数据和实际案例数据进行有效综合,对船坞双排钢板桩围堰稳定性进行了可靠度分析,发现该方法比常规方法更准确.李小军等[20]、丁勇春等[21]利用有限元法对船坞坞口临海基坑中非等长双排钢板桩围护结构进行了分析,发现排桩布置形式及受荷条件的差异导致该类结构的变形及受力性状与陆上基坑存在明显差异.虽然较多学者对临海基坑工程双排钢板桩支护结构开展了系列研究,但缺少针对波浪作用下非等长双排钢板桩结构的计算模型及其内力变形规律的理论分析.
综上所述,目前双排桩计算模型通常是针对等长双排桩结构建立的,对于非等长双排钢板桩结构的适用性难以考究,且现有针对临海基坑非等长双排桩结构的研究多采用数值模拟、室内试验及工程监测分析,缺少用于临海工程支护结构设计的理论支撑.本文结合临海基坑非等长双排钢板桩的受荷及结构特点,对规范模型中前、后排桩的约束形式及土压力分配模式进行了调整,并对桩间土与排桩相互作用力的计算方法进行了改进,提出临海基坑非等长双排钢板桩结构计算模型,以分析波浪作用下此类结构的内力变形性状规律.
1 非等长双排钢板桩计算模型及内力变形计算方法
1.1 非等长双排钢板桩计算模型
现有国家规范中的双排桩计算模型适用于半无限土体空间中的等长双排桩支护结构,该计算模型根据比例系数对桩间土初始土压力进行分配,并假设桩间土为薄压缩层,利用土体压缩模量计算桩间等效弹簧刚度,以考虑桩间土体与排桩的相互作用.但临海基坑支护结构前后排桩非等长且连续的布置形式使计算模型中排桩初始土压力分配方法不再适用,同时计算模型中桩土相互作用力的计算方法未考虑土体压缩模量随深度的变化规律[22],造成桩土作用力的计算误差随土层深度的增加而变大.
大量实际工程证明,若将双排钢板桩假定为悬臂梁,则按桩顶位移相等条件计算其受力性状与实际情况存在较大偏差,而将前、后排桩视为独立单排桩进行计算时,又无法考虑双排桩支护结构的整体性及相互作用.本文结合临海基坑工程地层及结构受荷条件,对规范计算模型中排桩土压力、桩土相互作用力的计算方法及排桩约束形式进行改进.首先,规定后排桩B 临海侧嵌固端以上作用海水压力及波浪力,嵌固端以下作用主动土压力;前排桩A 基坑侧开挖面以下部分作用地基土抗力;双排桩桩间侧均受桩间土主动土压力作用.其次,假设桩间土为连接前、后排桩的等效受压弹簧以考虑桩土相互作用力.最后,考虑实际工程中双排桩结构竖向位移较小,对结构水平位移及内力影响不显著,且排桩底部均为自由端,不存在弯矩,故假设双排桩底端均为固定铰支座.此外,由于双排桩顶部与混凝土圈梁整体浇筑,具有较大刚度,故将非等长双排钢板桩结构视为平面刚架结构进行计算.改进后的计算模型如图1 所示,其中桩间土抗力的等效弹簧刚度根据考虑深度变化的土体压缩模量计算,地基土抗力按m法计算.
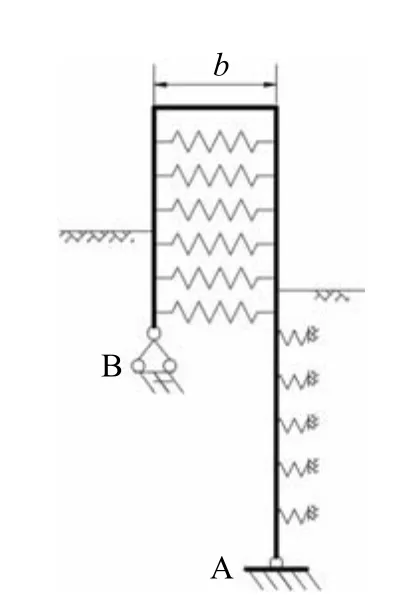
图1 非等长双排钢板桩计算模型
桩间土对前、后排桩的综合作用力与地基土水平抗力计算式分别为
式中:Fzk为桩间土综合作用力;Es,0.1~0.2为桩间土压缩系数,取计算深度处土层压缩模量均值;z为计算深度;ξ为影响系数(2.5~10.0),根据地层特性取值,土层越坚硬,ξ越小;Δ(z) 为计算深度处前、后排桩挠度差值,当两者相对位移减小时为正值,当两者相对位移增加时取Δ (z)=0 ;b为排桩排距;γ为土层平均重度;Ka为主动土压力系数;KF为地基土水平抗力;m为地基土水平抗力系数的比例系数;ωA(z)为计算深度处基坑侧排桩A 的挠度.
1.2 非等长双排钢板桩内力变形计算方法
非等长双排钢板桩计算模型为超静定平面刚架结构,排桩底部为固定铰支座,顶部与圈梁刚接,当结构受到海洋波浪作用力时,桩间土体产生形变,以系列独立受压的弹性支撑形式作用在前、后排桩上,此时前、后排桩相当于竖向放置在弹性地基上的梁而受到桩间土反作用力,因此可根据文克尔弹性地基梁理论计算排桩截面的内力及挠曲变形.由材料力学可知,
式中:θ为计算转角;ω为计算深度处排桩挠度;M为计算弯矩;EI为抗弯刚度;Fs为计算剪力.
任一计算深度处的结构微段如图2 所示.建立力与力矩平衡方程并忽略剪力对结构挠度影响,得到
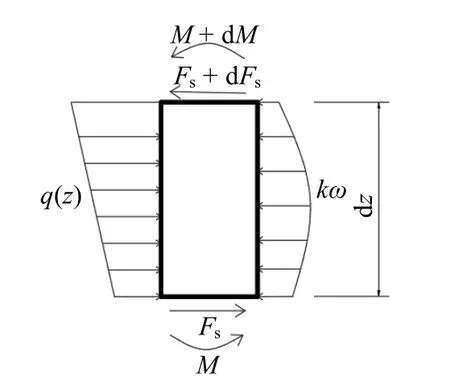
图2 计算深度处结构微段
式中:k(z) 为计算深度处弹簧刚度系数;q(z) 为计算点处荷载大小.
由于计算模型中考虑了等效弹簧刚度随计算深度的变化规律,最终的挠曲微分方程(4)为四阶变系数微分方程,无法利用连续积分、分离变量、常数变易等方法求出解析解,因此,按照幂级数法对结构挠度方程进行近似求解[23],并根据结构边界条件,联解得到结构任意截面处的内力及变形分布.特别地,前排桩嵌固段计算深度处的弹簧刚度远大于桩间土弹簧刚度,由式(4)可知,前排桩嵌固段内力及变形的计算结果将存在较大不同,影响其悬臂段的内力及变形,而圈梁只能传递集中弯矩及桩顶位移,故前、后排桩的内力及变形将存在一定的差异.
2 非等长双排钢板桩计算模型验证
为验证非等长双排钢板桩计算模型的合理性,在不考虑波浪作用的情况下,分别利用有限元数值模拟软件以及非等长双排钢板桩计算模型对浙江岱山某城防海塘工程中非等长双排桩结构的内力变形性状进行计算分析.
2.1 工程概况
岱山县城防海塘位于岱山本岛东南沿海侧,东起大浦门村,西至浪激渚二村,整体呈东西走向,横贯高亭镇.本工程除局部塘段采用透空式结构海塘轴线外移和局部塘段沿滨港道路布置调整外,基本沿原海塘走向进行加固建设,加固后海塘轴线全长约8.5 km.
2.2 材料参数及计算模型
该海塘工程的主要地层有: ①素填土、②淤泥质粉质黏土、③粉质黏土、④含砾沙粉质黏土、⑤强风化凝灰岩、⑥中风化凝灰岩.各土层主要物理力学指标见表1,强度指标参照直剪试验中的固结快剪取用,其中重力加速度取g=10 m·s-2.
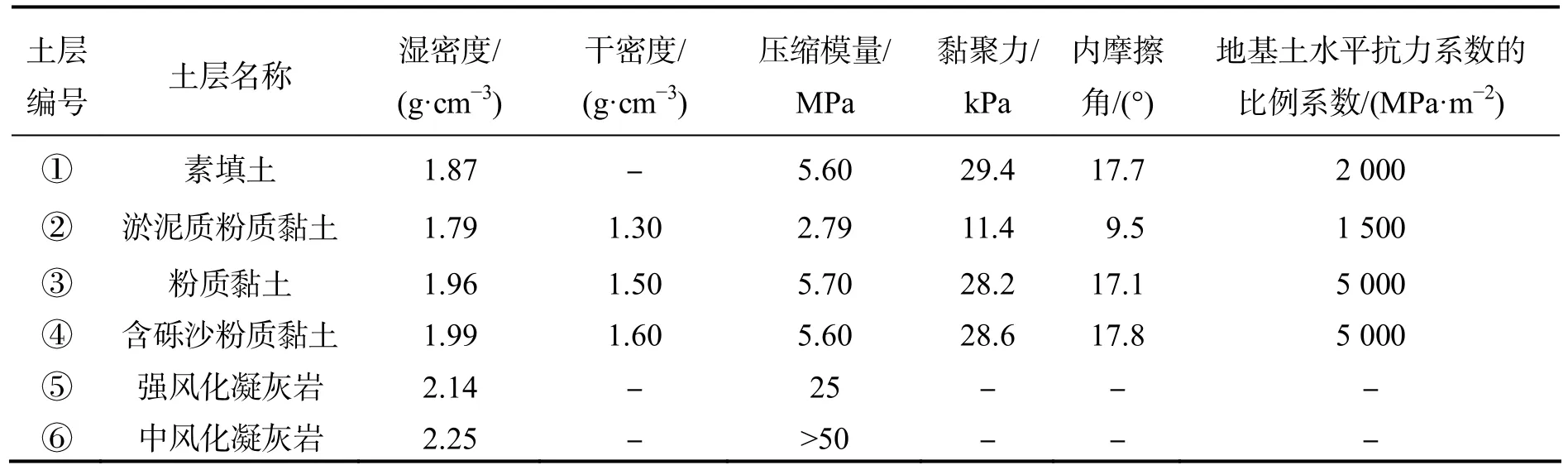
表1 各土层物理力学指标
基坑开挖计算深度9 m,底部高程-11 m;基坑临海侧泥面标高-8 m.基坑支护结构为连续布置双排钢板桩,基坑侧排桩A 长26 m,临海侧排桩B长16 m,顶部标高均为-2 m;排桩A、B排距为4 m;圈梁兼挡浪墙为钢筋混凝土结构,高4 m.基坑支护结构剖面如图3 所示,材料参数见表2.

表2 结构构件参数

图3 临海基坑剖面
水文条件: 波浪波高H=2 m,波长L=25 m,周期T=4 s,临海侧排桩前计算水深d=6 m,泥面高程-8 m,海水重度Hγ=10.5 kN·m-3.
2.3 有限元数值模型
本文采用岩土工程专用软件PLAXIS2D 建立二维数值模型,根据工程施工特点及土层条件采用可考虑剪切及压缩硬化的HS 模型作为土体本构模型,土体破坏准则参照Mohr-Coulomb 破坏准则.HS 模型包含强度、刚度、地下水、界面等多个参数,根据土层特性及以往模型参数的经验积累即可确定,其中刚度参数对于结构分析尤为重要,根据参考手册取值建议,对土层刚度参数做如下规定:为减小模型边界对计算结果的影响,建立了全尺寸模型x×y=50 m×100 m.双排钢板桩以及圈梁兼挡浪墙均采用板单元进行模拟,波浪荷载采用线荷载进行模拟,并分步对土层单元进行开挖降水,模型网格如图4 所示.
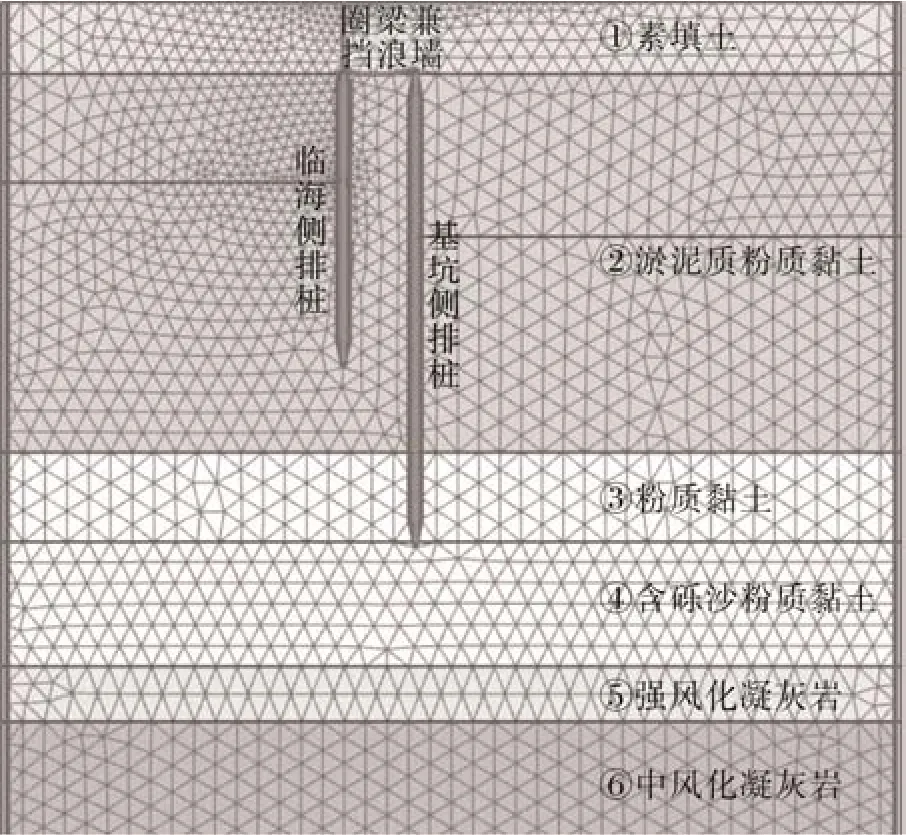
图4 计算模型网格
2.4 计算结果分析
基坑支护结构受荷后的弯矩及水平位移是衡量结构稳定性的重要指标,为评价非等长双排钢板桩计算模型的合理性,与有限元数值模型进行了对比分析.
图5 为无波浪作用时双排钢板桩结构的弯矩分布规律.由图5 可知,无波浪作用时,基坑侧排桩弯矩大致呈“抛物线”型分布;临海侧排桩弯矩则呈“S”型分布.两种计算方法得到的前、后排桩弯矩分布规律近似,弯矩值最大误差约为8.5%.
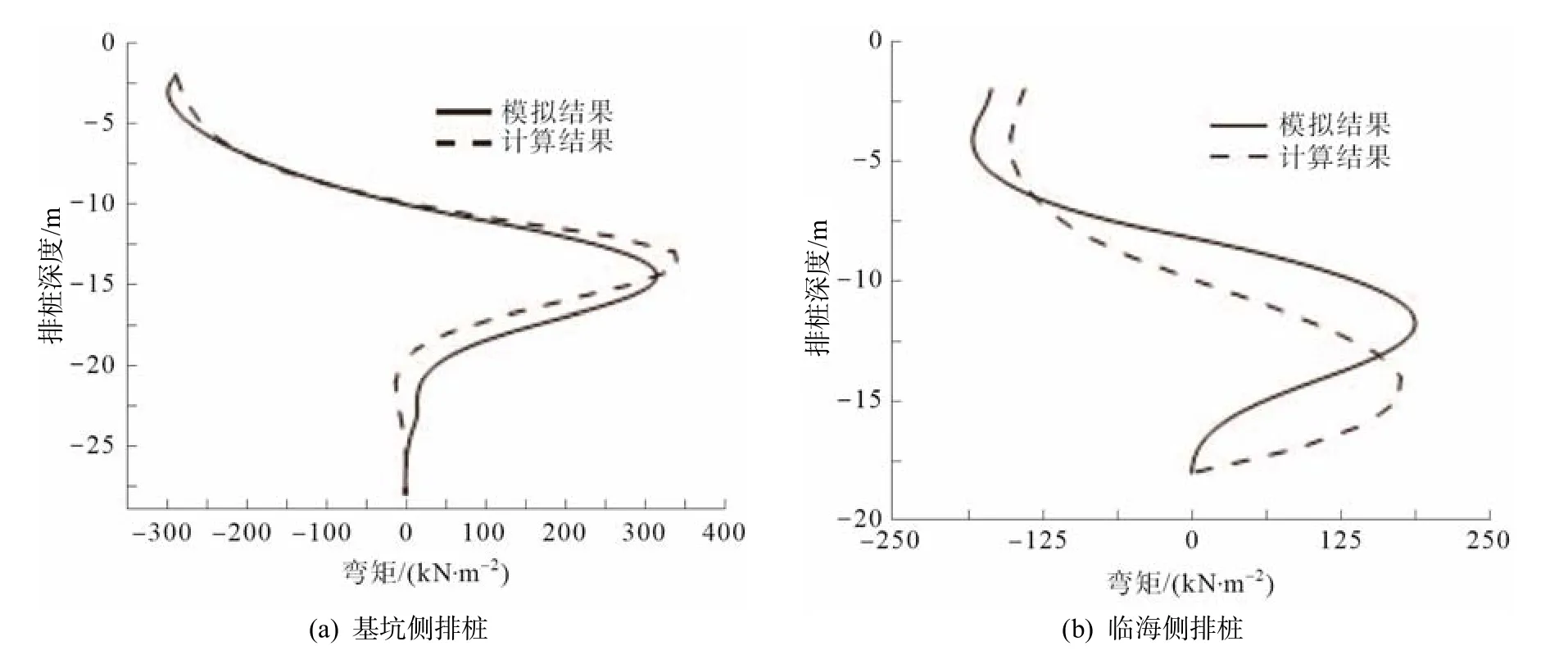
图5 无波浪作用非等长双排钢板桩弯矩分布
图6 为无波浪作用时非等长双排钢板桩的水平位移分布规律.由图6 可知,无波浪作用时,前、后排桩水平位移分布规律存在较大差异,但最大值相等且均出现在桩顶.基坑侧排桩水平位移随深度增加而减小的速率较快,在排桩中部已几乎减小为0,大致呈“对数函数”型分布;临海侧排桩的水平位移随深度增加而减小的速率较慢,排桩底部尚存在极小位移,大致呈“线性函数”型分布.两种计算方法得到的前、后水平位移分布规律亦十分近似,数值最大误差约为9.3%.
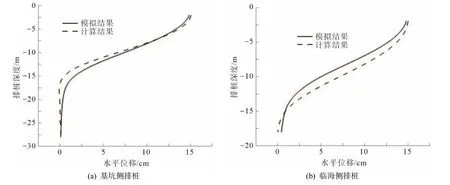
图6 无波浪作用非等长双排钢板桩水平位移
根据上述对比结果可知,两种方法具有较好的一致性,证明非等长双排钢板桩计算模型较为合理,适用于波浪作用下临海基坑非等长双排钢板桩支护结构内力变形性状的分析.
3 波浪作用对临海基坑非等长双排钢板桩的影响分析
海洋环境下临海基坑支护结构受到周期性波浪作用,为研究波浪作用对结构内力变形的影响,参照《港口与航道水文规范》[24]将波浪视为直接作用在结构上的荷载,利用非等长双排钢板桩计算模型对结构内力变形性状进行分析.
依照上述规范,本工程中水文条件宜考虑为作用在直墙式建筑上的立波,如图7 所示,经计算:波峰压力在静水面以上H处为0,静水面处达到最大值PBF,max=γH=21.00 kPa,泥面处达到最小值PBF,min=γH∙{ch[2π(d-d1)/L]/ch(2πd/L)}=8.86 kPa;波谷拉力在静水面处为0,静水面以下hs=(πH2/L)[cth(2πd/L)]=0.46 m 处达到最大值PBG,max=γ(H-hs)=16.17 kPa,泥面处达到最小值PBG,min=γH/ch(2πd/L)=8.86 kPa.上述计算将静水面以下深度z处的波峰压力进行了简化,总波浪力计算结果(89.80 kPa)相对规范方法(82.48 kPa)误差约为8.9%,简化较为合理.
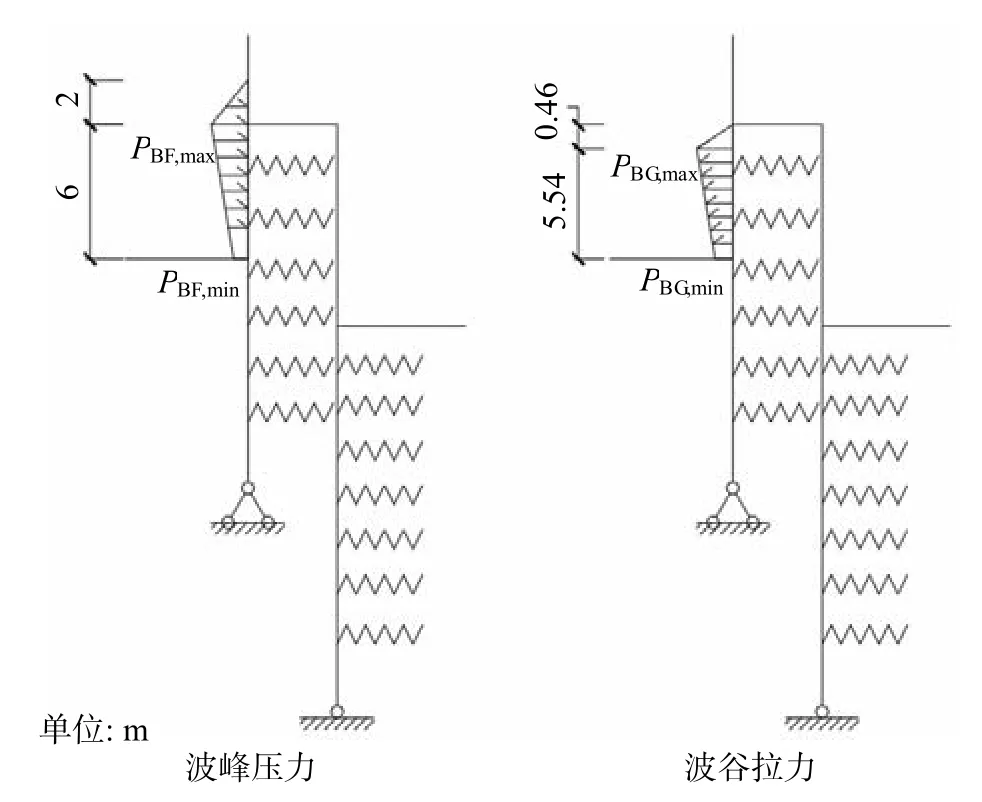
图7 波浪作用计算简图
3.1 波峰作用影响
图8 为波峰作用下非等长双排桩弯矩分布规律.由图8 可知,波峰作用下,前、后排桩的弯矩分别呈“抛物线”及“S”型分布,相较于无波浪作用时未发生太大变化,前排桩弯矩峰值达到-640 kN·m-2,出现在排桩顶部与圈梁连接处;后排桩弯矩峰值达到-326 kN·m-2,出现在与圈梁连接处稍靠下处,前、后排桩弯矩峰值相较于无波浪作用时均增大约121%.
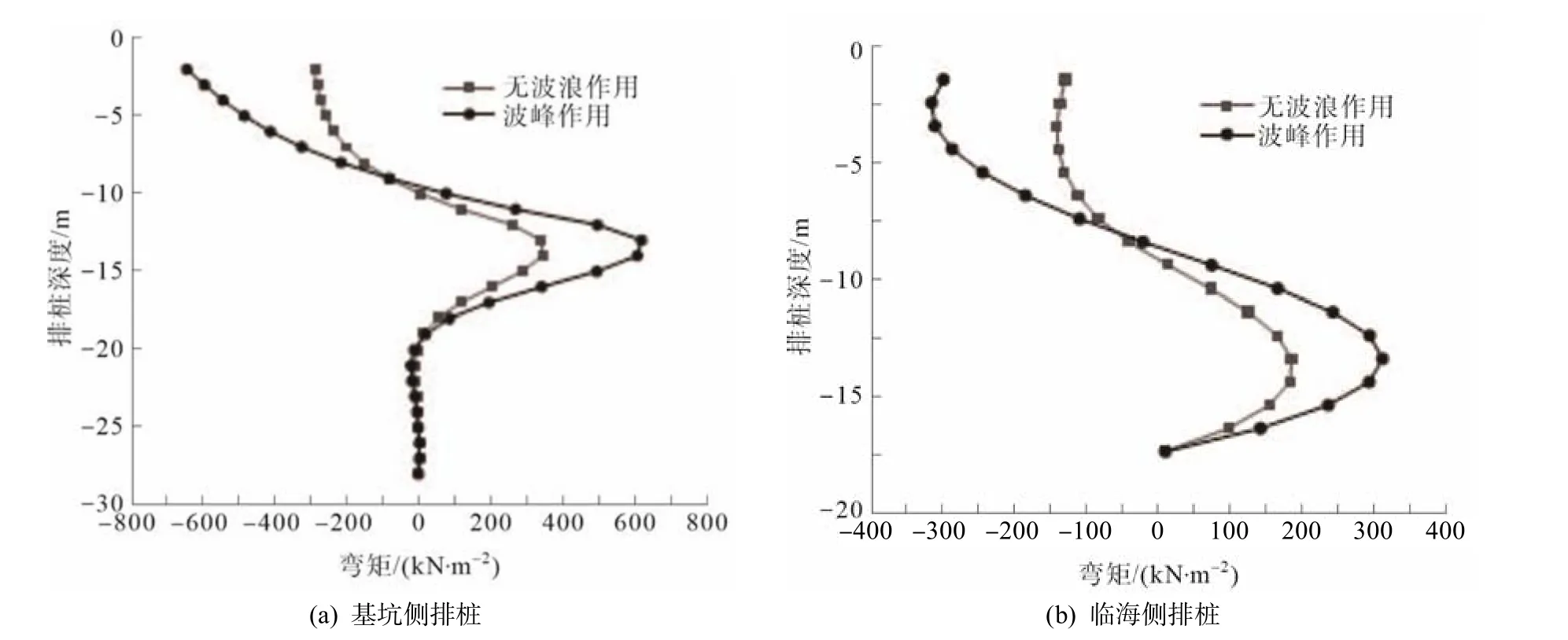
图8 波峰作用下非等长双排钢板桩弯矩分布
图9 为非等长双排桩受波峰压力作用时的水平位移分布规律.由图9 可知,前、后排桩受波峰作用时的水平位移分别呈“对数函数”及“线性函数”型分布,同样与无波浪作用时相近,水平位移最大值出现在桩顶,达到28 cm,对比无波浪作用时增加约87%.此外,临海侧排桩整个桩长范围内的水平位移均有不同程度增大(66%~95%),受波峰作用影响显著;基坑侧排桩嵌固深度超过10 m 部分的水平位移不受波峰作用影响.
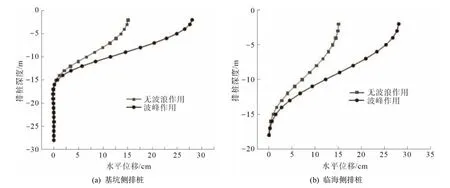
图9 波峰作用下非等长双排钢板桩水平位移
3.2 波谷作用影响
图10、图11 给出了非等长双排钢板桩的弯矩分布及水平位移受波谷作用影响的规律.由图10、图11 可知,波谷作用下,前、后排桩弯矩分别呈“抛物线”和“S”型分布,同样与无波浪作用时相近.前、后排桩弯矩值相较于无波浪作用时则存在不同程度的减小,基坑侧排桩弯矩在排桩中部达到最大值175 kN·m-2,减小约49%;临海侧排桩弯矩最大值出现在距排桩底部1/5 桩长处,约为100 kN·m-2,减小约43%;前、后侧排桩水平位移分别呈“对数函数”和“线性函数”型分布,较无波浪作用时同样未发生较大变化,最大值为6.8 cm,出现在桩顶处,减小约55%.
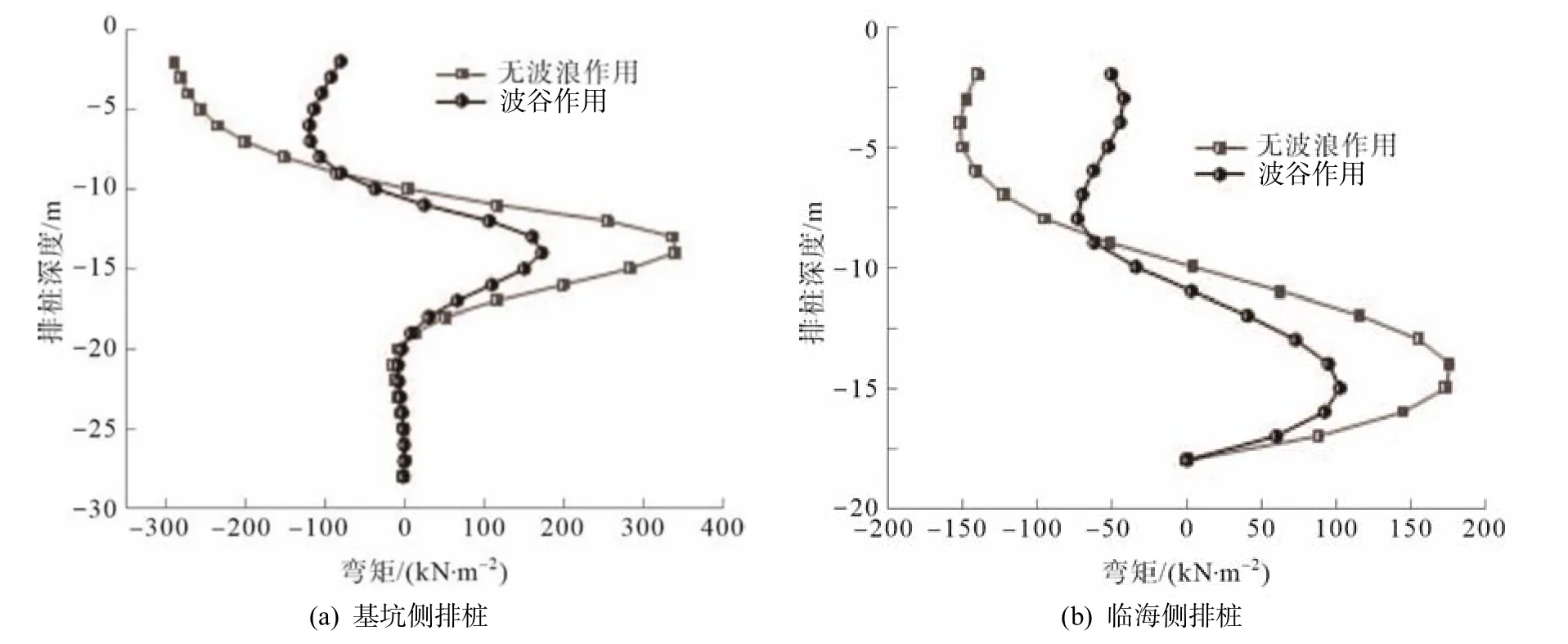
图10 波谷作用下非等长双排钢板桩弯矩分布
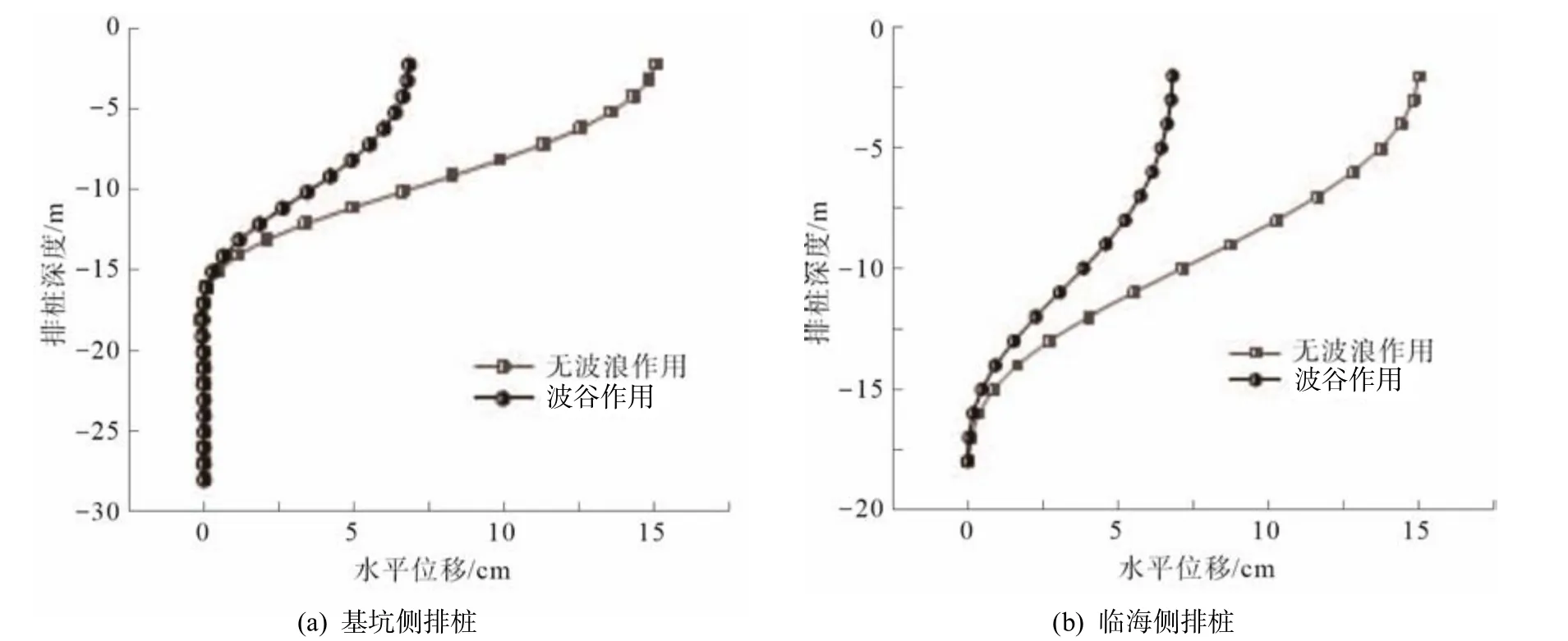
图11 波谷作用下非等长双排钢板桩水平位移
4 结论
根据临海基坑工程支护结构地层及荷载环境特点,提出非等长双排钢板桩计算模型,结合数值模拟结果进行了对比验证,并分析了波浪作用下结构内力变形性状的规律,主要结论如下:
(1)建立了非等长双排钢板桩计算模型,该模型能够考虑桩间土压缩模量随深度变化规律及波浪作用影响,弯矩、位移计算结果对比数值模拟结果最大误差约为9%,具有较好的一致性,能够用于波浪作用下临海基坑支护结构内力变形性状的研究.
(2)无波浪作用时,前、后排桩弯矩分别呈“抛物线”和“S”型分布,前排桩弯矩峰值约为后排桩的两倍;前、后排桩水平位移分别呈“对数函数”和“线性函数”型分布,最大值相等且均出现在桩顶.
(3)波峰作用下,前、后排桩弯矩分别呈“抛物线”和“S”型分布,水平位移分别呈“对数函数”和“线性函数”型分布,较无波浪作用时均无太大差异;前、后排桩弯矩峰值分别达到-640 和-326 kN·m-2,相较于无波浪作用时均增大121%左右,水平位移最大值约为28 cm,相较无波浪作用时增大87%左右.
(4)波谷作用下,前、后排桩弯矩及水平位移分布规律同样与无波浪作用时相近,数值相较于无波浪作用时存在不同程度的减小.前、后排桩弯矩峰值分别为175 和100 kN·m-2,相较于无波浪作用时减小49%左右;双排桩桩顶水平位移最大值为6.8 cm,减小约55%.
