熔模铸造机车车钩工作应力与疲劳寿命仿真
2024-02-02郭志启龚海军李福军高正源孙鹏飞钟发勇
郭志启,龚海军,李福军,高正源,孙鹏飞,钟发勇
(1.重庆交通大学机电与车辆工程学院,重庆 400047;2.天长市兴宇交通装备科技有限公司,安徽 滁州 239300)
0 引言
车钩是列车车厢之间及车厢与机车连接最重要的零部件之一,起到串联列车并保证安全运行的作用。车钩传递相邻车辆所受的拉、压动载荷,当列车启动或制动时,相邻两车厢之间的车钩装置会出现较大的纵向冲击。如纵向瞬时应力超过车钩限值,将破坏车钩装置甚至车厢结构,导致严重事故;如长期使用,则车钩在交变动载荷作用下容易疲劳,形成疲劳断裂导致安全事故。
鉴于车钩铸件的重要性,熔模铸造生产必须保证车钩具有足够的强度和疲劳寿命[1-2],为此学者们对车钩疲劳性能进行了大量研究。为预测车钩疲劳寿命,田长亮等[3]采用旋转弯曲疲劳试验,测定了3种不同强韧性匹配的25MnCrNiMoA钢的疲劳极限,研究表明,强韧性对重载车钩材料的高周疲劳行为影响显著。孟庆民等[4]对货车的20个服役车钩钩舌进行了裂纹扩展过程的全程监测,基于95%存活率和90%置信度得出了剩余寿命与对应的裂纹长度关系。朱涛等[5]将基于线路实测得到的载荷谱作为重载货车车钩服役环境,进行疲劳台架试验,基于假设分布对车钩退化数据进行拟合,得到了寿命预测图。
通过疲劳试验来研究车钩的疲劳裂纹扩展和寿命具有直观、准确的优点,但也费时费力,通过理论与仿真结合的方式来估算出疲劳寿命则快速有效。吴刚等[6]使用Palmgren-Miner累计疲劳损伤准则对车钩缓冲装置进行了寿命周期内的疲劳分析。MOHAMMADI等[7]采用包括临界面法在内的多种方法对不同工况下的车钩成功进行了疲劳寿命预测。Yin等[8]提出了基于SMOTE-Bootstrap-Bayes估计的重载货车钩身服役可靠性分析方法,对于提高试验数据的利用率,降低试验成本,有效评估钩身疲劳寿命具有重要的理论和应用价值。Ren等[9]建立了真实接触约束下的有限元模型,根据巴黎定律和NASGRO方程预测剩余寿命,对铸钢重型车钩提出了检验周期的建议。
综上所述,对机车车钩的疲劳寿命进行数值仿真预测研究必要且经济有效。为评估某熔模铸造柴田式密接机车车钩的使用性能,基于车钩材料的组织分析和力学性能测试结果,建立车钩工作的有限元模型,选择典型工况和载荷谱进行应力-应变及疲劳寿命仿真分析,以期对该车钩的工作应力状态和疲劳寿命进行分析和预测,并为此类车钩的检修和进一步优化提供参考。
1 熔模铸造车钩的组织与性能
车钩采用熔模铸造而成,材质为E级钢ZG25MnCrNiMo。外形轮廓尺寸为594 mm×370 mm×350 mm,属大型复杂熔模铸件[10]。车钩纵轴横断面中最小截面积为0.008 m2,其几何模型及实物如图1所示。
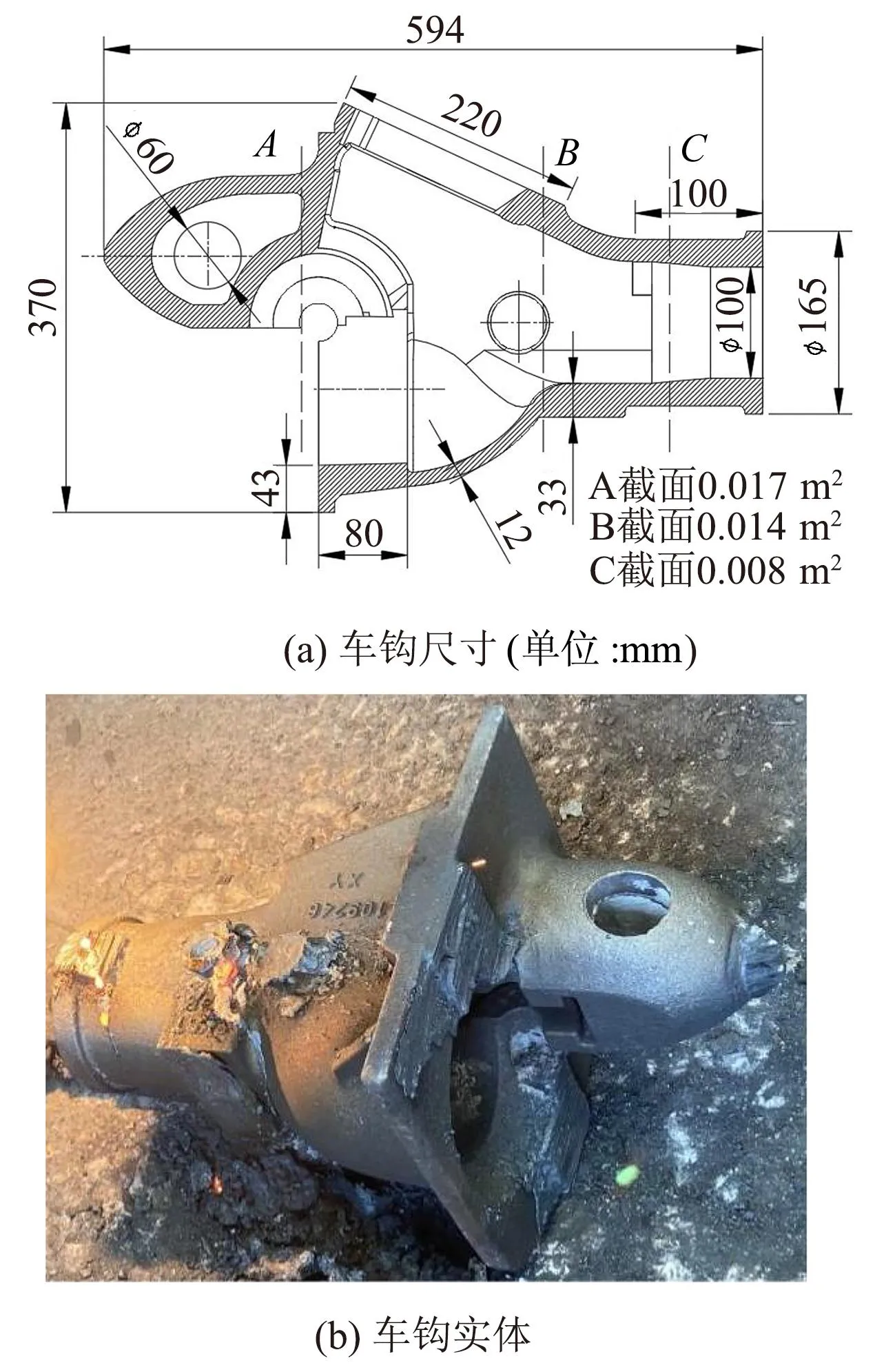
图1 车钩主要尺寸及实物
对车钩铸件的铸态和热处理态(正火+910 ℃淬火+2 h 590 ℃回火)分别取样,在光学显微镜(OM)和扫描电镜(SEM)下观察微观组织,结果如图2所示。

图2 熔模铸造车钩微观组织
由图2(a)可见,车钩在铸态下的组织主要由珠光体和铁素体组成。铸态组织与TB/T 2942.2—2018《机车车辆用铸钢件 第2部分:金相组织检验图谱》中1级标准相比,其铸态晶粒大小与分布形貌均超过标准的要求。车钩铸件经正火预备热处理和调质处理后,组织为细小且均匀的回火索氏体,见图2(b),在高倍SEM观察下,铁素体基体上分布着许多细小均匀的碳化物颗粒。从热处理前后的车钩铸件大平面区各切取6个试样进行拉伸测试,获得的数据取其平均值,数据如表1所示。
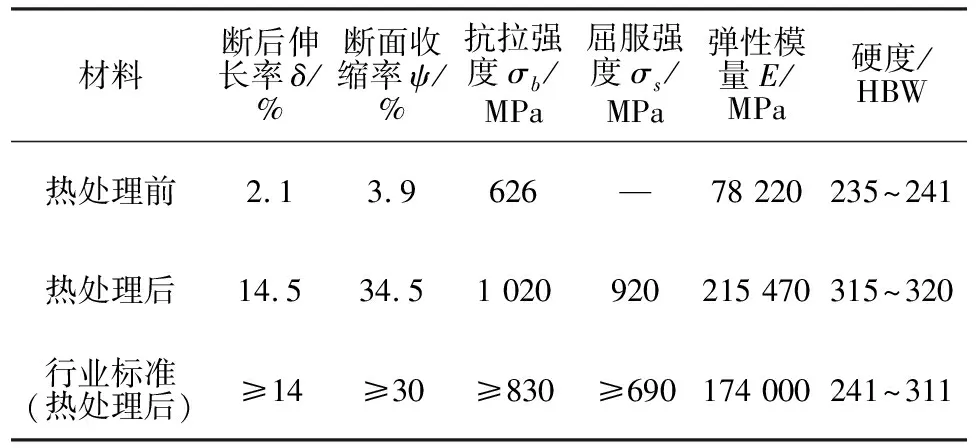
表1 ZG25MnCrNiMo车钩热处理前后力学性能平均值
拉伸试验结果显示,铸件在铸态下的抗拉强度处于550~675 MPa,其伸长率在1.5%~2.7%;经调质处理后,其抗拉强度达到900~1 450 MPa,屈服强度为920 MPa,而伸长率最高达14.5%,较之铸态有大幅度提升,这主要是正火+调质的热处理有效地细化了晶粒、改善了夹杂和偏析等缺陷。与铁道行业标准TB/T 2942—2015(热处理后)ZG25MnCrNiMo钢的主要机械性能参数相比[11],本研究中热处理态车钩满足使用要求。
对拉伸断口进行电镜观察,发现铸态试样未出现明显颈缩,断面解理面明显,属于脆性断裂,其断口微观形貌如图3(a)所示;而经过调质处理后的试样断口呈准解理断口特征,见图3(b),韧口呈现出不连续扩展,准解理小断面有许多撕裂棱,断裂性态介于解理断裂和韧性断裂之间,相比如铸态韧性有明显提升。

图3 断口形貌SEM图片
2 车钩工作原理及其有限元模型
2.1 疲劳寿命的仿真方法
在零件生命周期内,疲劳寿命就是裂纹萌生和裂纹扩展直到断裂过程所用的时间。在交变载荷作用下,裂纹的萌生或扩展是逐步形成的,多次循环加载后,结构的损伤量积累到一定量,使结构失去功能。目前疲劳寿命的预测主要有2种方法:应力寿命法和应变寿命法。应力寿命法基于应力-循环次数(S-N)曲线,它描述了应力幅值对应的疲劳循环次数[12]。这种方法仅适用于高周疲劳(104次以上),其结果保守,还可能会对实际不会疲劳的结构预测出疲劳破坏。应变寿命法基于应变-循环次数(E-N)曲线,描述了应变幅对应的疲劳循环次数。它不限于高周疲劳,精度高,仿真时计算速度比应力疲劳慢[13]。文章选择E-N法进行仿真。
2.2 车钩的连接与受力
两车钩连挂时,一侧车钩的钩头插入另一侧车钩钩头孔中,如图4(a)所示。这时凸锥的内侧面在前进中压迫对方的钩舌转动,使解钩气缸的弹簧受压,钩舌沿逆时针方向旋转40°。当两车钩连接面相接触后,凸锥内侧面不再压迫对方的钩舌,此时,由于弹簧的作用,使钩舌顺时针方向旋转恢复到原来的状态,即处于闭锁位置。
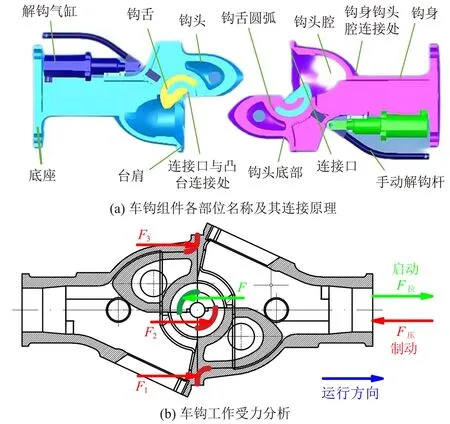
图4 车钩连接原理及工作受力分析
车钩主要用于连接车厢,故受力的方向为纵向。车钩间传递力的部位主要是钩舌部位,当列车启动时,车钩主要受到拉力的作用,此时车钩组件中主要是钩舌的圆弧面受力;当列车制动车钩受到压缩力时,车钩组件中主要是钩舌圆弧面和连接口位置受力,忽略重力,车钩工作时受力如图4(b)所示。
2.3 车钩工作有限元模型
由于车钩结构复杂、壁厚不均,所以对车钩采用四面体单元进行划分。为了得到更加精确的计算结果,全局网格划分从10 mm开始,逐步缩小划分网格的尺寸进行计算,直到应力结果变化小于3%,得出车钩应力集中的位置,此时车钩全局网格尺寸已缩小为1.75 mm。然后再对应力集中位置进行局部网格细化,最小网格尺寸划分为0.5 mm,如图5所示。划分好的装配体模型的节点总数为3 369 299个,单元数为1 924 534个。

图5 车钩网格划分
2.4 车钩载荷
车钩在启动和制动期间受到的拉伸和压缩载荷是最大的[14]。当列车启动时,车钩受到拉伸载荷,拉伸力瞬间达到最大值,随后逐渐衰减;列车开始平稳运行时,拉伸力趋于稳定;当列车制动时,车钩间受到压缩载荷,压缩力瞬间达到最大,随后逐渐衰减,直至列车停止时衰减为零。根据《地铁车辆车钩技术规范》要求,车钩及钩座应满足不小于1 000 kN的静压力,不小于800 kN的拉伸力,车辆平稳行驶时的最大拉力为600 kN。故静力学仿真分析采用上述载荷数据,目的是通过极限工作载荷的仿真分析,考察车钩的强度是否满足设计要求。
疲劳分析选用大秦线实测车钩载荷-时间历程编制的8级载荷谱[15]作为车钩工况加载。但由于柴田式密接车钩是用于城市轨道载人线路,与大秦线载货列车的最大载荷有差别,故对大秦线载荷最大幅值进行了修正,即幅值超过800 kN的一律取800 kN,大秦线的疲劳仿真载荷谱如图6中粉色折线所示。
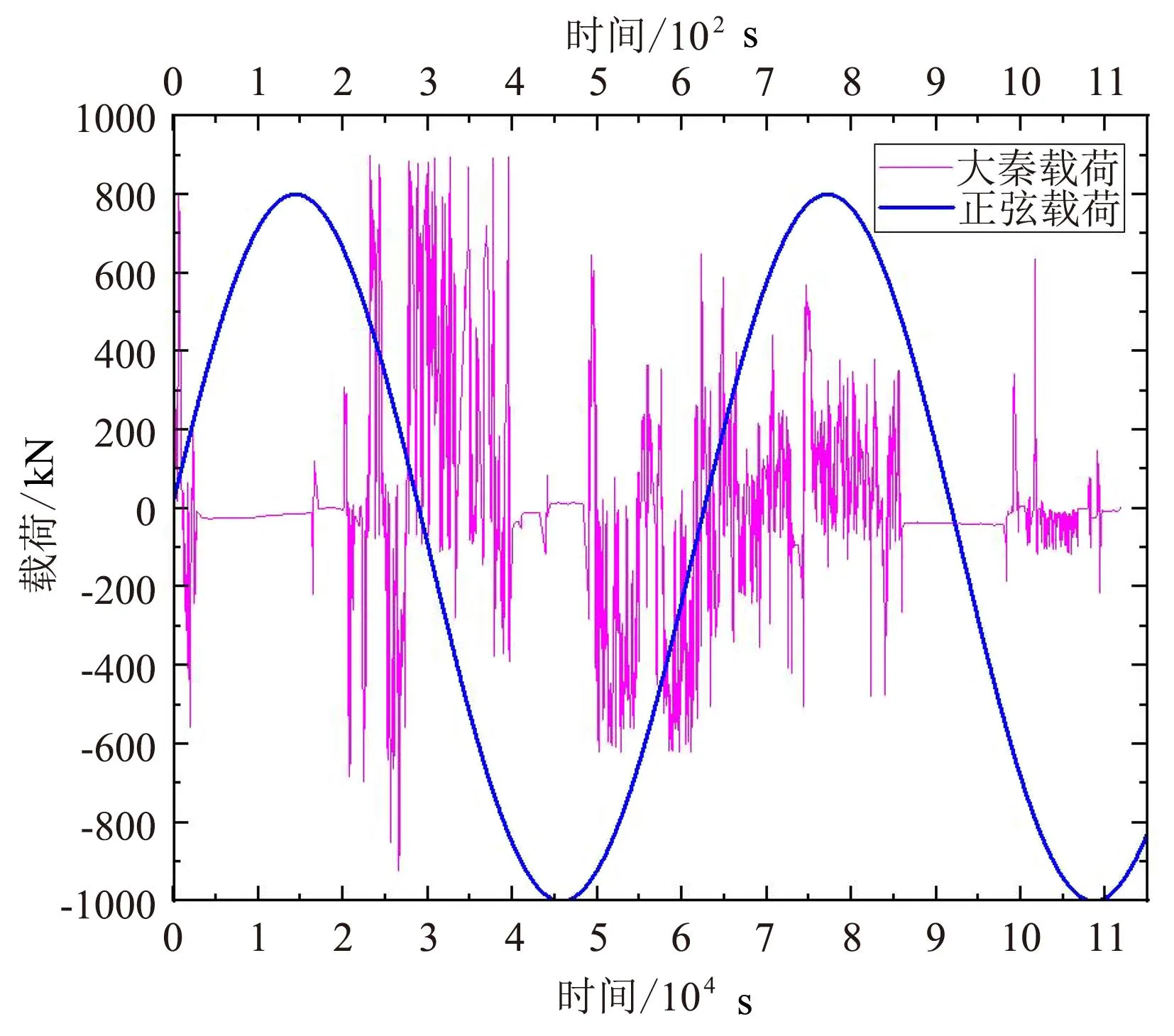
图6 大秦线车钩载荷谱与正弦载荷谱
大秦线是一条货运线路,且路况复杂,相对于在城市中运行的轨道车辆,在大秦线上运行载荷造成的损伤更大一些。为使仿真结果具有实用性和对比性,再以重庆最繁忙的地铁3号线为例进行疲劳分析。轨道交通运行中两站点之间主要是启动加速、匀速平稳运行、制动减速3个阶段,故可将载荷谱简化为图6中蓝色正弦波形的载荷进行模拟计算,其幅值采用地铁车钩技术规范要求的800 kN。
3 车钩力学性能仿真结果与讨论
3.1 静强度仿真分析
列车车钩分别承受600 kN、800 kN和1 000 kN的拉伸和压缩载荷,即在平稳运行工况、启动工况及紧急制动工况下,车钩的应力分布情况如图7(a)、(b)、(c)所示。从仿真结果分析可知,在平稳运行工况的600 kN静拉伸载荷下,车钩牵引端最大的应力为362.04 MPa,牵引端最大变形为2.41 mm;启动工况下,车钩所受最大应力为482.72 MPa,最大变形量为3.21 mm,较大值出现在车钩钩头底部的位置。从图4(b)中对车钩受力分析可知,车钩受到拉力时受力位置主要是钩舌的圆弧面,如图4(b)绿色圆弧所示,不在钩头的中心位置,因而会导致钩头受力不均,从而使钩头底部呈现最大应力。从仿真结果看,应力最大位置与应力集中的位置一致,见图7(a)、(b)圈选处。
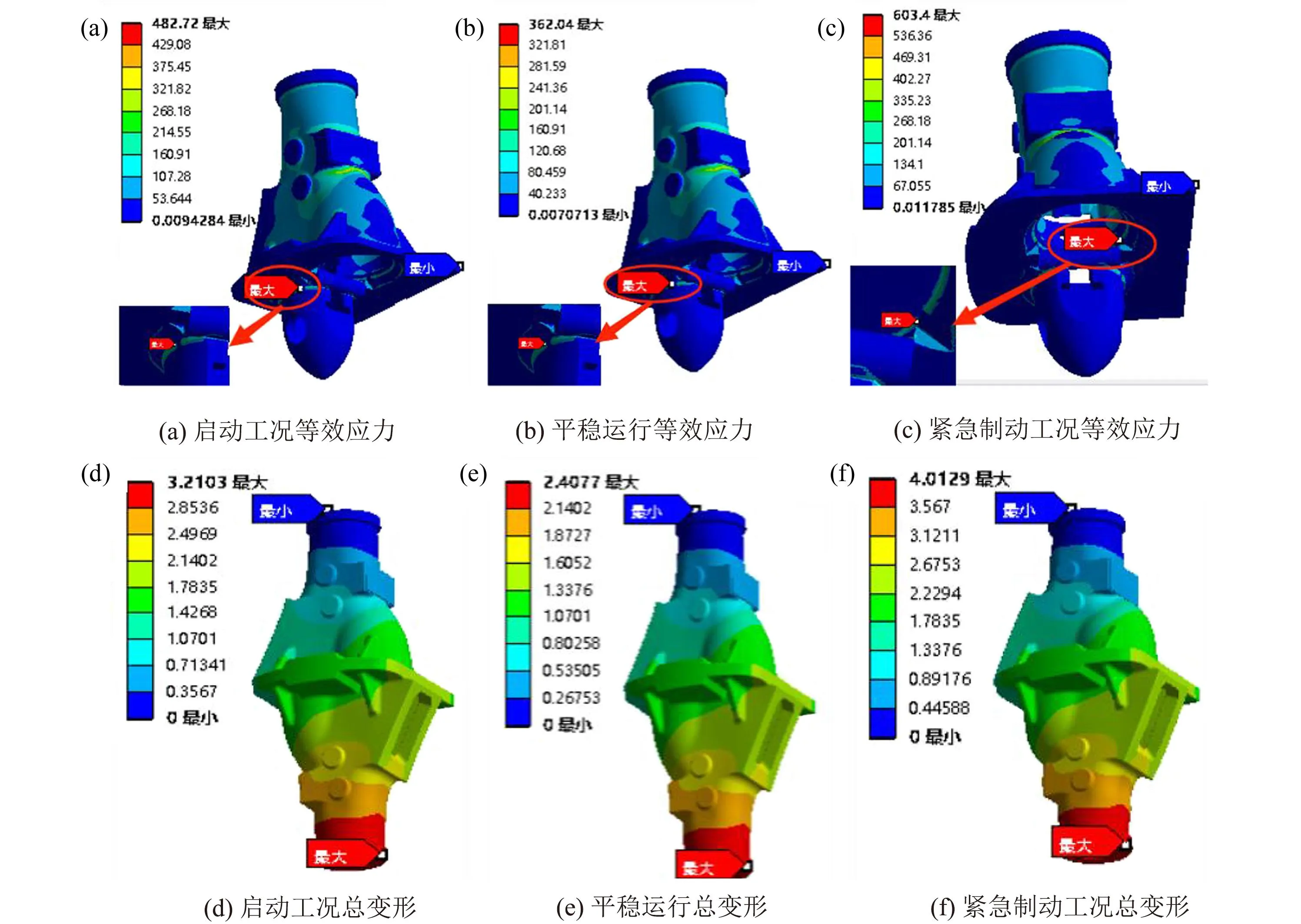
图7 车钩不同工况下的等效应力和总变形
由车钩材料力学测试结果(见表1)可知,车钩材料热处理后的抗拉极限平均为1 020 MPa,正常工况条件下的应力远小于材料的屈服极限。车钩材料热处理后的断后伸长率为14.5%,车钩除去钩头总长为430 mm,可计算出车钩最大可变形量为62.35 mm,由图7(d)(e)仿真结果可知,车钩启动工况下总变形3.21 mm,平稳运行最大总变形2.41 mm,远未达到最大可变形量,故车钩在正常工况下可安全使用。
列车行驶中动量巨大,紧急制动须采用常规制动1.5倍的制动力,即1 000 kN制动力的情况。从分析结果可知,在紧急制动工况下,车钩所受最大应力为603.4 MPa,最大变形量为4.01 mm,应力最大的位置是连接口与钩舌凸台附近,见图7(f)。从车钩受到压缩力的位置分析来看,主要是连接口和钩舌圆弧面,如图4(b)红色圆弧所示,由于连接口与钩舌凸台连接的位置形状复杂会出现应力集中的现象,这与仿真分析的结果一致,见图7(c)圈选处。同时,由仿真结果与力学试验结果分析,车钩在此压缩载荷下可以安全使用。
3.2 车钩疲劳分析方法与结果讨论
3.2.1疲劳分析方法
疲劳仿真主要研究车钩在受到拉伸-压缩循环应力作用下的结构损伤,主要方法是根据车钩在一次应力循环中受到的损伤量来估算车钩的疲劳寿命。在进行疲劳试验时,保持总应变幅值Δε/2不变,对各个试件用不同应变幅值进行试验,直至试件破坏,记录各次试验的疲劳寿命Nf,以应变幅值εa=Δε/2为纵坐标,以2Nf为横坐标在双对数坐标中画出log(Δε/2)-log(2Nf)曲线,即得到应变-疲劳寿命曲线。E级铸钢车钩材料的应变疲劳寿命双对数曲线如图8所示。
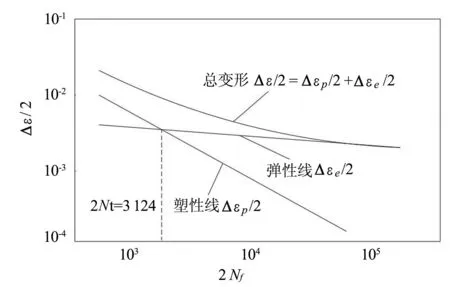
图8 E级钢的Δε/2-2Nf双对数关系曲线
依据疲劳理论,应力-疲劳寿命之间的关系为式(1):
(1)
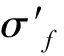


(2)
塑性应变-疲劳寿命的关系为式(3):
(3)

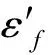
根据Manson和Coffin两人分析应变疲劳的试验结果,得出应变疲劳-寿命公式(4):
(4)

(2Nf)-1.030 23
(5)
将一次应力循环损伤量代入式(5),即可分析估计车钩的疲劳寿命。
3.2.2疲劳仿真结果与讨论
将材料测试获得的力学数据以及静强度仿真结果导入到ANSYS ncode模块中,在疲劳分析中设定钩舌的表面为铸造表面(-40 μm 1)大秦线载荷谱疲劳仿真分析 将大秦线实测载荷谱数据导入,利用应变-寿命(E-N)曲线,进行 Brown Miller 多轴疲劳分析和 Goodman 平均应力修正,ncode模块自行计算出车钩的载荷谱疲劳循环次数,结果如图9所示。由图9可见,车钩最易疲劳的位置出现在图9圈选位置,最低疲劳寿命为105.2次。 图9 疲劳寿命仿真结果 将易疲劳位置与前文图7静应力分析结果的应力云图比较可以看出,易出现疲劳的位置与前文静应力仿真中应力集中的位置一致。这些位置主要是车钩钩头的底部、连接口和钩身钩头腔连接处,因此在设计和加工环节对这些位置需要重视,在日常维护中也应重点监护。 加载的大秦线载荷谱全长15 000 km[17],而仿真结果表明车钩受交变载荷最恶劣处的寿命为105.2个循环载荷,将寿命数据代入式(6): C=l·n (6) 式中:C为可安全行驶总里程;l为载荷谱全长;n为车钩循环次数。则算得C=1 578 000 km。 2)重庆地铁3号线疲劳仿真分析 密接式车钩常用于高速列车、城市地铁和轻轨车辆。重庆地铁3号线总长56.4 km,列车每天运行6趟。如将车钩在大秦线工况上可安全运行的里程数,简单折算到重庆地铁3号线上进行比较,则可将数据代入式(7): (7) 式中:N为车钩寿命;C为车钩在大秦线上可安全行驶总里程;c为3号线总长;t为一天运行次数。 计算可得车钩在重庆地铁3号线的可运行寿命为12.8年。当然,以复杂路况的大秦线实际载荷谱来估算在城市轨道上的平稳运行寿命是不准确的。城市轨道两站点间的工况主要是启动加速、匀速行驶、制动减速,故可以正弦波作为载荷谱进行寿命评估。此外,车钩作为机车重要的连接和安全保障零件,需要考虑过载的情况,故以车钩800 kN载荷幅值及空载、半载和多种不同大小的过载载荷为条件进行疲劳仿真分析,同时通过静力学仿真计算出不同载荷下车钩内部最大内应力,绘制出车钩的疲劳寿命曲线,结果如图10所示。 图10 车钩疲劳曲线 由图10可见,车钩疲劳寿命随载荷(或车钩内部最大内应力)的降低而减小,当车钩常年工作在1 440 kN载荷时,车钩内部最大拉应力高达868.6 MPa,此时车钩只能经受2.6×104次正弦载荷,即理论上可安全工作0.26年。当车钩以600 kN载荷正常工作时,可经受5.1×107次正弦载荷冲击。当车钩载荷降低到580 kN时,此时车钩内部的最大应力为349.86 MPa,车钩疲劳寿命曲线变为水平,也就是说车钩理论上不会发生疲劳。按常规,一般钢铁材料的疲劳试验循环基数要求为107级,故车钩正常运行时能承受5.1×107次正弦载荷冲击是完全满足使用要求的。 此外,钢铁材料的对称循环疲劳强度值σ-1一般约为其抗拉强度值σb的1/2左右,而脉冲疲劳强度σ0一般比对称疲劳强度低。本文车钩材料的抗拉极限平均为1 020 MPa(见表1),根据图10疲劳寿命曲线可见,车钩在加载800 kN幅值的正弦波载荷时,车钩内部最大内应力为482.7 MPa,即在此载荷下疲劳强度为482.7 MPa。而车钩加载680、640、620、600 kN幅值的正弦波载荷时,其疲劳寿命依次达到1.8×107、3.6×107、5.1×107、7.3×107次循环,而此组疲劳寿命显然是已达到钢铁疲劳循环的基数107级的要求,此时对应的疲劳强度值分别为410.2 MPa、386.1 MPa、373.9 MPa、361.9 MPa,比车钩理论的对称循环疲劳强度约值510 MPa低,这也表明疲劳寿命仿真的结果是可信的。 重庆3号线共45站,每辆列车每天运行6趟,将图10中不同载荷下车钩的循环次数代入式(8): (8) 式中:N为车钩寿命;n为车钩最低循环次数;t为一天运行次数;a为车站数量。 则可估算出车钩在800 kN和600 kN幅值正弦波载荷下运行的寿命分别为31.5年和740.7年。根据《地铁车辆车钩技术规范》要求,车钩的使用寿命应不低于30年,熔模铸造车钩热处理后远超规范中的使用年限要求,但如果列车频繁出现过载,则应适时检修。 1)扫描电镜下观察熔模铸造车钩材料,发现其组织均匀,晶粒细小,无明显铸造组织缺陷;拉伸测试表明铸态下的抗拉强度最高可达675 MPa,热处理后抗拉强度最高可达1 540 MPa,评价可达1 020 MPa,组织和性能满足车钩要求。 2)车钩在启动、平稳运行、紧急制动3种工况下,应力和变形远小于车钩许用屈服强度和变形量,车钩满足服役要求。 3)通过仿真绘制了车钩正弦载荷-疲劳寿命曲线,车钩加载大秦线载荷谱的疲劳寿命最高可达12.8年,重庆轨道3号线在800 kN幅值正弦谱的疲劳寿命为31.5年,车钩满足使用要求,仿真结果可为车钩的检修提供依据。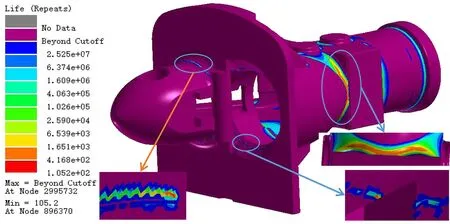

4 结论
