抗侧滚扭杆的轻量化设计方法及实例

罗 燕,李 鹏,刘文松,陈天鸥,彭伟伦,邹敏佳

(株洲时代新材料科技股份有限公司,湖南 株洲 412000)

0 引言

目前国内外大部分高速客车和地铁车辆转向架均采用了抗侧滚扭杆装置,以有效抑制车体侧滚角,降低车辆柔度系数[1]。抗侧滚扭杆装置利用金属弹性杆受扭转时产生扭转变形而提供反力矩,来抑制车辆的侧滚振动,而不影响车辆的伸缩、横摆、点头、摇头及浮沉等运动[2]。

轻量化是现代轨道车辆设计的重要目标。一方面,轻量化减轻了车辆自重,节约了原材料,降低了制造成本;另一方面,轻量化减少了车辆的牵引力和制动力,实现了节能降耗,并有效地减少了线路的负荷,节约其维修费用。可见,轻量化具有重大而长远的经济效益。抗侧滚扭杆装置中质量最大的部件一般是直扭杆,而最核心的、强度最薄弱的部件也是直扭杆,因此对直扭杆进行轻量化设计非常重要且必须谨慎。目前直扭杆制造已普遍采用屈服强度大于1 300 MPa的超高强度钢,在钢制材料强度上再提高已有一定困难。而复合材料由于其各向异性的特点,难以在直扭杆批量制造时保证其性能的一致性,且刚度稳定性和耐环境性能也存在不确定性,尚在研究探索阶段,目前主要在非关键部件如垂向连杆上得到了试验验证[3]。直扭杆主要受扭转产生扭转变形从而提供反力矩,横截面切应力有芯部小、表面大的特性,目前长直轴深孔加工技术已较为成熟,空心直扭杆对抗侧滚扭杆装置的减重效果显著,对抗侧滚扭杆的空心结构轻量化设计方法进行分析很有必要。

1 空心结构轻量化设计方法分析

1.1 等体积法分析

设一长度L0、直径D0的实心直扭杆,其面积A0、极惯性矩Ip0、抗扭截面系数Wp0、在扭矩T作用下的最大切应力τ0max:

(1)

(2)

(3)

(4)

另设一长度L1、外径D1、内径d1的空心直扭杆(见图1),并令α=d1/D1,由于空心直扭杆和实心直扭杆长度和体积相等,则其面积也相等,那么空心直扭杆的外径D1、极惯性矩Ip1、抗扭截面系数Wp1:

(5)

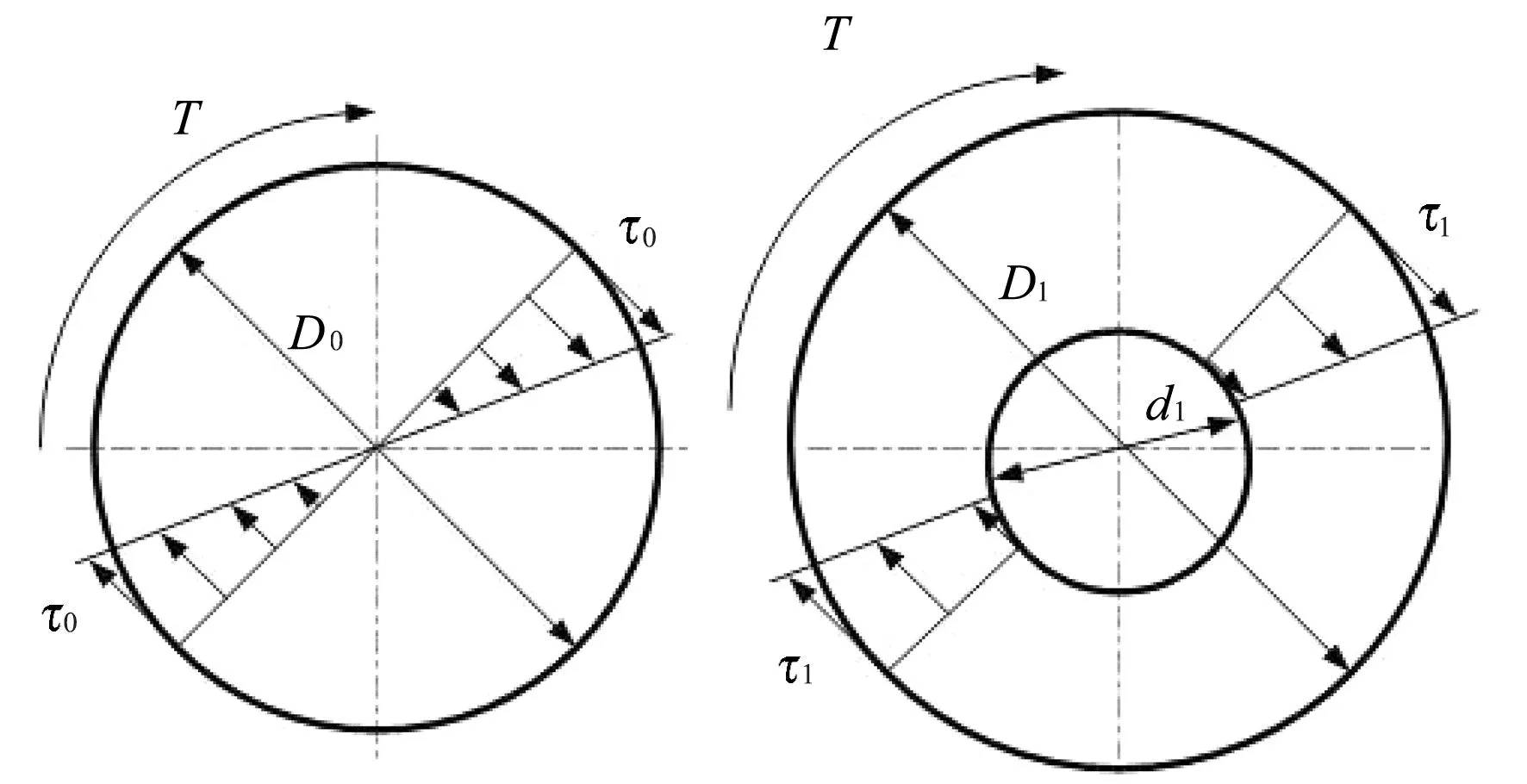
(a)实心直扭杆 (b)空心直扭杆

(6)

(7)

假设原实心直扭杆的直径D0为50 mm,长度L0为1 000 mm,以直扭杆内外径之比α为自变量,来探究在等体积条件下直扭杆各几何参数变化规律,如表1所示。

表1 等体积、不同内外径之比α条件下,直扭杆的几何参数

根据表1和图2可发现,在等体积条件下,随着直扭杆内外径之比α的增大,极惯性矩Ip1和抗扭截面系数Wp1均迅速增加,且极惯性矩增加得更快,其原因是极惯性矩是直径的四次函数,而抗扭截面系数是直径的三次函数。实际工程中,直扭杆需要满足一定的扭转刚度和承载能力,刚度约束将在下一章节分析。针对承载能力,由于空心直扭杆的抗扭截面系数是增大的,若选用力或扭矩工况分析会无法求解,因此可以选取弹性试验中的最大扭转角度为约束条件进行解析。

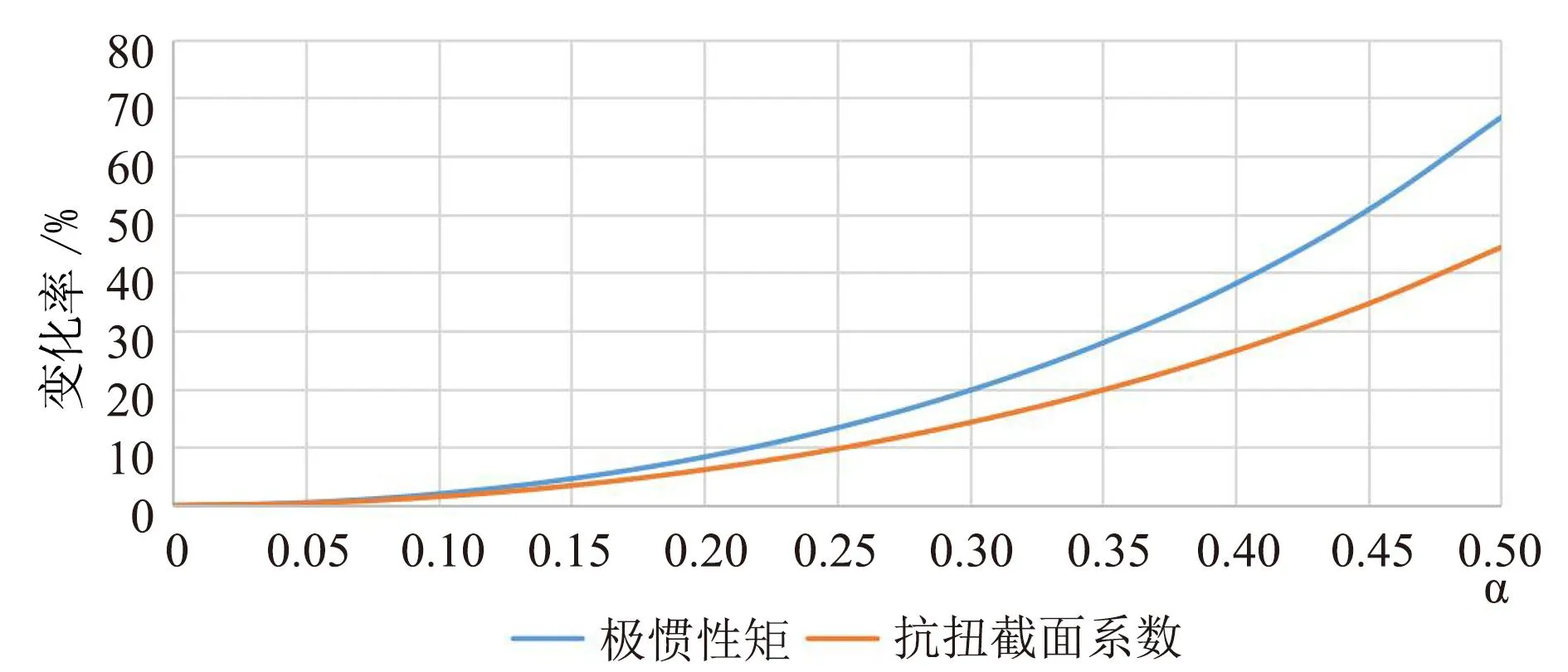
图2 等体积条件下横截面积的几何参数变化

TB/T 3285标准中对直扭杆弹性试验规定:应在技术规范中明确直扭杆的最大扭转角,并在试验时持续2 min以上不发生永久变形,回复自由状态时其位置误差不能超过10′。直扭杆弹性试验最大扭转角φ在实际工程中常取12°,即0.21 rad。空心直扭杆应满足在最大扭转角下,其最大切应力τ1max不超过材料的许用切应力[τ]。在弹性范围内,在扭矩T作用下空心直扭杆的扭转角度φ及最大切应力τ1max:

(8)

(9)

τ1max≤[τ]

(10)

联合上式解得解析空心直扭杆的内外径之比:

(11)

式中:[τ]为材料的许用剪切应力,EN 15049中建议值为700 MPa[5];G为剪切模量,取80 GPa。

根据式(11),当直扭杆长度L无限长时,会解出α无限接近1的结果,而过薄的圆筒受扭时,筒壁可能发生皱折而丧失承载能力[6],因此当L足够长时需要注意薄壁直扭杆的扭转稳定性。但在实际工程中,直扭杆长度L一般介于1 000 mm到3 000 mm之间,直扭杆直径D0一般介于20 mm到100 mm之间,因此上式具有广泛的工程应用价值。

假设原实心直扭杆的直径D0为50 mm,长度L0为1 000 mm,则可求得同体积空心直扭杆的内外径之比α≤0.63,此时外径D1≤64.38 mm,内径d1≤40.56 mm。若该空心直扭杆尺寸超过限值,则其12°最大扭转角的弹性试验有失效风险。

1.2 等刚度法分析

直扭杆的核心作用是利用自身扭转弹性变形蓄能而提供扭转反向扭矩,单位扭转角度下所提供的扭矩称为扭转刚度,扭转刚度是直扭杆的核心性能指标。抗侧滚扭杆装置的刚度对倾覆系数、柔性系数、浮心高度都有较大影响。特别是当取消抗侧滚扭杆装置时,如果转向架二系空气弹簧的横向跨距和转向架的垂向刚度较小,则车辆的倾覆系数将超出标准要求,抗倾覆能力较差[7]。在实际工程中,直扭杆的扭转刚度往往被设计为一个定值,因此基于等刚度的空心直扭杆分析很有必要。

根据章节1,依然假定初始实心直扭杆的长度L0为1 000 mm,直径D0为50 mm。在等刚度的条件下,假定空心直扭杆的长度L2为1 000 mm不变,内孔直径d2为一个变化量,外径D2等参数则在等刚度的约束下,随内孔直径d2变化而变化。因此,在某一内孔直径d2条件下,与实心直扭杆等刚度空心直扭杆的外径D2、横截面积A2、抗扭截面系数Wp2分别为:

(12)

(13)

C2=C0

(14)

式中:C0为初始实心直扭杆的扭转刚度;C2为空心直扭杆的扭转刚度。

联合上式,解得:

(15)

(16)

(17)

由于实际工程中,内孔直径受限于加工工艺、刀具尺寸等因素,不可任意取值,因此对内孔直径d2取值按梯度进行假定,对比分析不同内孔直径d2条件下的直扭杆各几何参数变化规律,如表2所示。

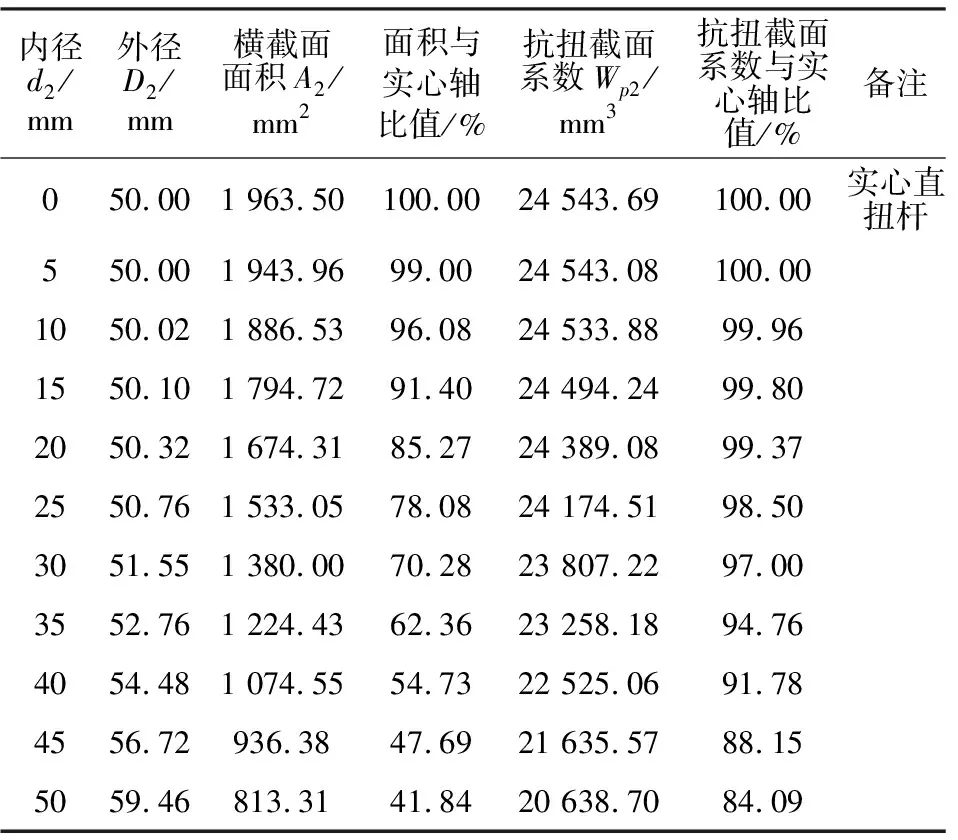
表2 等刚度、不同内径d2条件下,直扭杆的几何参数

根据表2和图3可发现,在等刚度条件下,随着直扭杆内孔直径d2的增大,横截面面积A2迅速减小,而横截面的抗扭截面系数Wp2减小得很缓慢。其原因是在刚度不变的情况下,横截面对中心轴的极惯性矩不变,此时横截面的抗扭截面系数仅与直扭杆外径成反比关系,而横截面面积为直扭杆外内径的二次方关系。也就是说当直扭杆刚度设计确定后,选用空心直扭杆结构可以大幅节约产品材料而减轻产品重量,而其抗扭能力减小得很少,即相同工况载荷下其应力增加或强度减小得很少,这个规律对实际工程中直扭杆的轻量化、低碳设计意义重大。

图3 等刚度条件下横截面积的几何参数变化

2 设计实例

2.1 空心直扭杆内孔确定

根据某型抗侧滚扭杆装置的技术输入,侧滚刚度要求2.3×(1±10%)MN·m/rad;弹性试验要求为扭杆扭转12°并保持2 min,回复后变形不超过10′;疲劳工况为±18 kN循环200万次。抗侧滚扭杆装置的侧滚刚度主要与空心直扭杆结构尺寸有关,根据侧滚刚度要求,并结合强度要求和加工工艺等因素,确定空心直扭杆的内孔直径为20 mm。

2.2 空心直扭杆强度验证

空心直扭杆选用了扭杆常用材料52CrMoV4,材料参数如表3所示。

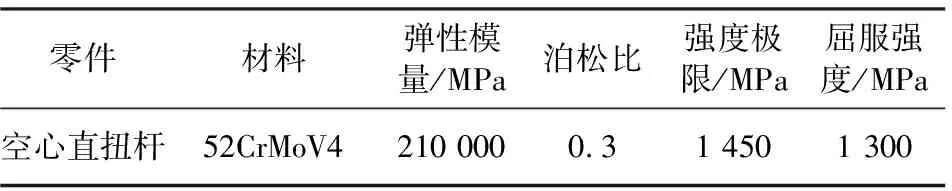
表3 空心直扭杆金属材料力学特性

在确定材料各项性能参数后,采用ABAQUS软件对结构进行了详细的有限元分析计算,在极限工况下,空心直扭杆的最大应力位于中间部分圆弧过渡处,大小为669.9 MPa(见图4),低于其材料的屈服强度1 300 MPa,安全系数为1.94,即空心直扭杆结构和材料可满足强度要求。

2.3 装置试验验证

参照技术要求,对该型空心直扭杆装置进行了刚度、弹性、应力、疲劳试验。试验结果表明空心直扭杆侧滚刚度满足2.3×(1±10%)MN·m/rad要求;空心直扭杆弹性扭转变形量在10′以内;应变片测得应力结果与有限元分析结果误差不超过5%;通过200万次疲劳试验(见图5),试验过程中对应变片进行监测显示载荷均匀可靠,试验后对抗侧滚扭杆装置进行探伤检测,未发现任何裂纹扩展和断裂现象,具体试验结果如表4所示。

图5 空心直扭杆装置疲劳试验

3 结语

空心直扭杆是抗侧滚扭杆轻量化设计的可行方案之一,且具有理论基础和工程应用业绩。采用等体积法,基于最大扭转角12°的弹性试验约束条件,解析出空心直扭杆内径取值条件,以某一扭杆明确的材料、直径、长度为实例,得出空心直扭杆的约束条件为内外径之比α≤0.63。采用等刚度法,以实例进行推导计算,发现在等刚度条件下,随着空心直扭杆内径的增大,其横截面面积迅速减小,而横截面的抗扭截面系数减小得很缓慢。得出了当扭杆刚度

设计确定后,选用空心直扭杆结构可以大幅节约产品材料,而其抗扭能力减小得很少,即相同工况载荷下其强度减小得很少的规律。以某轨道车辆用扭杆装置的技术要求为输入依据,对空心直扭杆装置进行计算模拟、产品制造、试验验证,结果表明空心直扭杆装置满足设计要求,并通过了200万次疲劳试验验证。