空间运动方程快速求解器设计与实现

王晓蕾, 黄章骞, 房 旭, 宋宇鲲

(合肥工业大学 微电子学院,安徽 合肥 230601)

空间运动方程(space motion equation,SME)作为一种高阶常微分方程,是研究运载火箭、近地导弹、近地航天器等传统飞行器轨道力学的关键手段之一[1];采用合适的方法计算出SME相对精确的数值解,在运载火箭的轨道控制中扮演着无可替代的角色。因为SME具有多变量、高复杂度、大迭代次数和高精度需求的特点,所以方程求解需要进行庞大的计算,影响计算速度。学者们开展了大量的研究工作以提高SME的求解速度,文献[2]采用牛顿迭代法减少迭代次数,实现简化弹道快速设计和发射诸元快速装订;文献[3]基于均匀实验设计、牛顿迭代法和逐步回归分析的理论提出一种发射诸元拟合方法,建立发射诸元的快速计算模型;文献[4]在研究标准弹道计算方法和分析偏差弹道快速计算方法的基础上,设计海基潜射弹道导弹诸元快速计算的总体方案,并通过仿真证明方案的正确性和可行性;文献[5]建立用Kriging插值实现弹上扰动引力快速计算的数学模型,结合一种飞行弹道仿真结果证明弹载计算机能够满足该方法对速度和精度的要求;文献[6]基于解析预报与数值寻优相结合的方法,利用线性回归方法建立弹道方程多项式并得到对应初值,然后采用Levenberg-Marquardt方法搜索诸参数的精确解,在精度要求不高的情况下可以使用该方法快速计算诸元。

上述研究从多个角度对空间运动方程及弹道方程的求解进行加速和优化,但仍然很难满足实际应用中的实时性需求。四阶经典龙格库塔法(classical Runge-Kutta method of order four,RK-4)和四阶Adams预测校正法(fourth-order Adams predictor-corrector method,Adams-4)2种直接数值求解常微分方程的方法在实际应用中得到广泛应用。借助硬件对上述方法的常微分方程初值问题求解过程进行加速,已经在众多领域得到研究和应用。文献[7]基于经典微分方程数值解法RK-4,提出一种可重构的微分方程解算器,通过指令实现对不同微分方程运算路径的重构;文献[8]采用复用的RK-4求解结构,在现场可编程逻辑门阵列(field programmable gate array,FPGA)平台上完成基于五阶鼠笼式感应电机模型的风力电机动态仿真模型设计;文献[9-11]在FPGA上分别实现陈氏混沌系统、Pehlivan-Wei混沌系统和6阶混沌系统的求解,在资源效率和吞吐率上表现良好;文献[12]完成RK-4求解弹道方程的FPGA设计与实现。

上述研究表明,采用硬件对微分方程求解进行加速具备可行性。针对传统的软件求解无法满足SME实时性求解的问题,选择求解速度更快的Adams-4方法作为SME的主方法,并以RK-4作为启动方法,采用硬件对SME的数值求解进行加速,在保证有效精度的情况下将运算速度提升一个数量级,对SME的求解具有重大工程价值和研究意义。

本文设计的空间运动方程快速求解器(space motion equation fast solver,SMEFS)通过动态配置SMEFS内部运算器连接关系,在同一硬件分时实现RK-4、Adams-4算法,有效地提高资源利用率,提升系统主频。最后完成空间运动方程快速求解器的FPGA设计与实现。

1 空间运动方程数值求解分析

1.1 空间运动方程介绍

根据文献[1]的结论,发射坐标系下5自由度空间运动方程为二阶常微分方程,表达式为：

(1)

其中：dx/dt=vx;dy/dt=vy;dz/dt=vz。式(1)等号右侧的表达式均为中间变量,由其他复杂运算计算得到,包括三角/反三角函数运算、矩阵运算、开方运算和四则运算,计算过程涉及发射方位角、火箭静推力等,计算复杂且运算量庞大,具体表达式本文不展开描述。

1.2 高阶常微分方程数值求解方法计算原理

1.2.1RK-4方法

RK-4方法作为经典的单步法,由于计算精度高、可自启动的特点,在工程上广泛应用于求解一阶或高阶常微分方程。式(1)所述二阶常微分方程通过降阶处理得到式(2)所示的抽象方程,对应的RK-4计算表达式为：

(2)

(3)

其中：h为迭代步长;n=0,1,…;初值为y0=α,z0=α′。

1.2.2Adams-4方法

Adams-4方法是线性多步法,充分利用每一次的运算结果,提升计算速度;通过预测和校正,减小运算结果的截断误差。式(2)方程组的Adams-4的计算表达式[13]为：

(4)

2 系统设计

2.1 系统结构

SMEFS采用数据驱动的管道式计算结构,系统架构如图1所示,系统采用的数据格式为IEEE754标准的双精度浮点数。

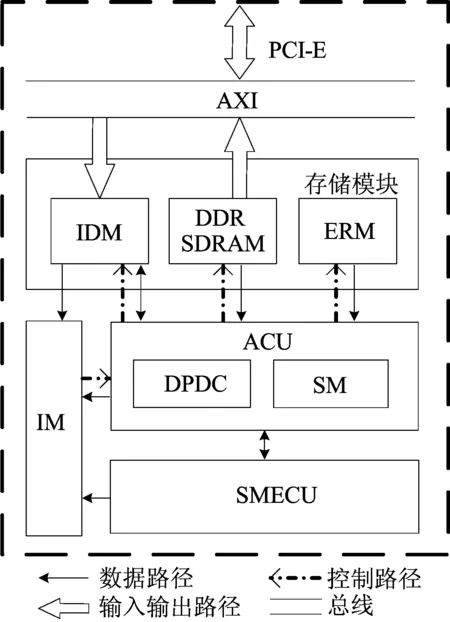
图1 SEMFS系统架构

系统包括算法控制单元(algorithmic controller unit,ACU)、数据路径动态配置(data path dynamic configuration,DPDC)模块、状态管理器(state manager,SM)、空间运动方程计算单元(space motion equation calculate unit,SMECU)、迭代管理器(iterative manager,IM)、初始化数据存储器(initial data memory,IDM)、DDR SDRAM、高效复用的存储器(efficient reuse of memory,ERM)以及用于PCI-E数据传输的AXI数据总线。以式(4)的一次求解任务为例,SMECU负责计算函数值f,而ACU完成变量y、z的线性组合计算。

SMEFS采用折叠变换技术在同一硬件上实现RK-4、Adams-4方法电路的分时复用,即通过对折叠后功能单元间的链接关系进行精准切换和动态配置,实现数据路径的动态配置,在有限的资源上完成SME数值求解任务。SMEFS根据主机通过PCI-E接口下发的程序和数据独立完成求解工作并将数据回传至主机。

2.2 ACU和SMECU设计方案

ACU通过折叠对运算器资源实现复用,根据RK-4、Adams-4方法的折叠集,动态配置数据路径,完成对应的方法运算任务,为SMECU提供函数计算所需的输入。

1) RK-4的折叠集分析与重映射。RK-4方法的硬件实现结构可分为展开式和迭代式[14]。迭代式结构是通过折叠技术对方法的运算任务进行重映射,减少功能单元数目的前提下满足性能需求,该结构为在有限的资源上完成基于该算法的复杂方程求解提供可能。实现迭代式结构到硬件的映射,需要对RK-4方法完整的数据流图(data flow graph,DFG)进行重定时,得到折叠因子和每个复用功能单元对应的折叠集,并根据折叠因子和折叠集完成对功能单元链接关系进行精准切换和动态配置[15]。

参考式(3)所述的递推关系发现,在对RK-4方法的硬件结构进行折叠时,折叠因子N可选择2、4;考虑到空间运动方程的复杂度,为了尽可能地节约资源,本文选择的折叠因子为4。由于RK-4方法作为Adams-4方法的启动方法,只完成3次迭代,则RK-4方法的折叠结构运行的任务数为l=3。因此,RK-4方法每次迭代任务在折叠结构上的折叠集为{Nl,Nl+1,Nl+2,Nl+3}。对RK-4方法的运算任务拆分和映射得到其折叠集为{SM1,SM2,SM3,SM4},折叠集中每个运算任务的表达式为：

(5)

对折叠集进行分析发现,折叠集中4个运算任务的运算链长度也不同,任务SM4的运算链较长,折叠后所需的功能单元最多;此外任务SM2中部分运算与SM1中的M1相关。同理,任务SM3与SM2相关,SM4与SM1、SM2、SM3相关。基于折叠集中任务依赖关系复杂、任务分配不均的问题,对折叠集中的任务进行重定时,优化任务间的依赖关系,均衡分配多个任务的复杂度,对RK-4方法运算任务进行重映射,得到的DFG如图2所示。

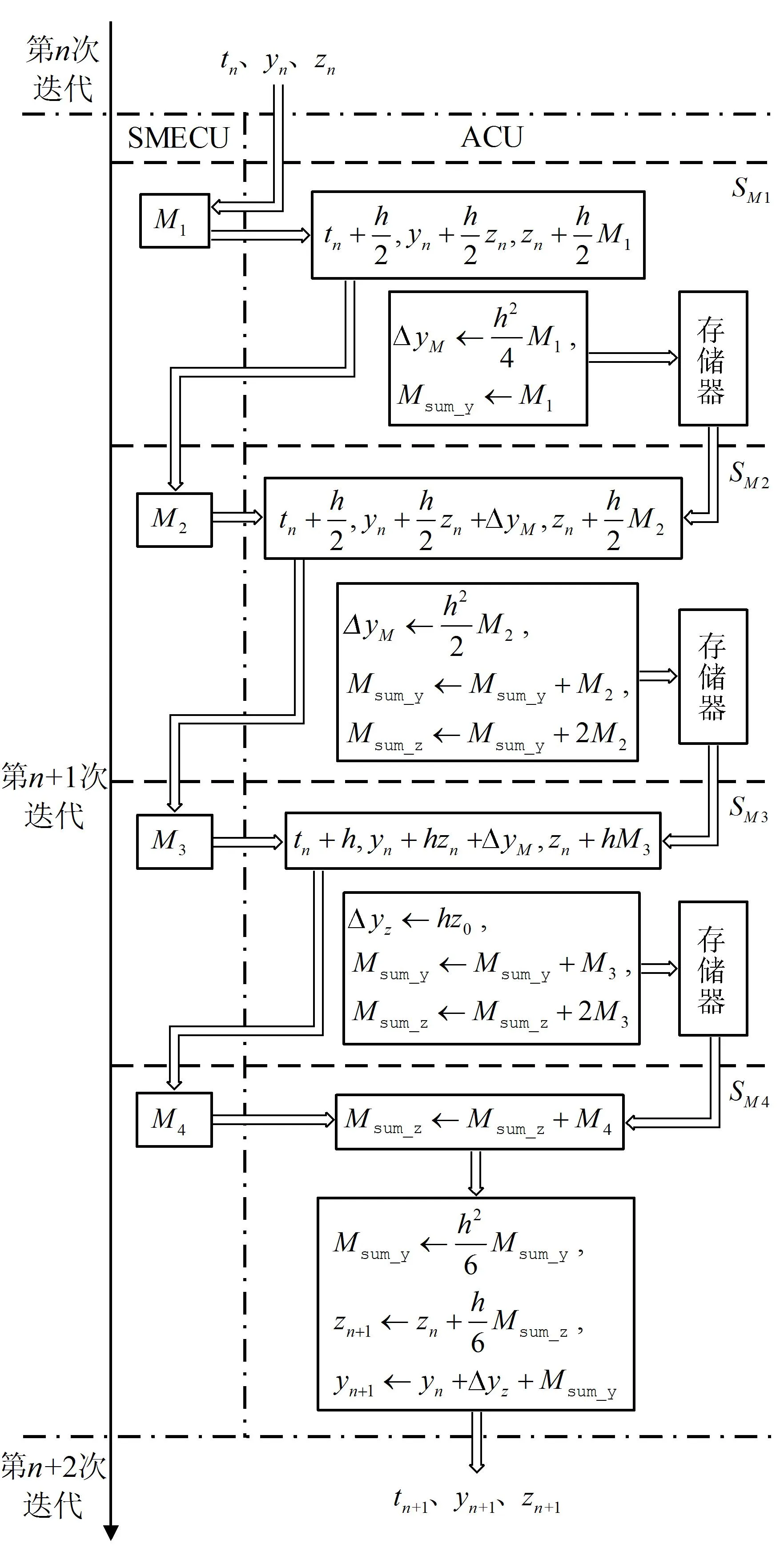
图2 RK-4方法折叠结构下优化的DFG

2) Adams-4的折叠集分析与重映射。参考式(4)所示的Adams-4方法递推关系,对Adams-4方法采用折叠方法分析,其折叠因子只能为2。针对该折叠因子和方法递推关系,得到其折叠集为{SA1,SA2},折叠集中的运算任务表达式为：

SA2={yn+1,zn+1,f(tn+1,yn+1,zn+1)}

(6)

由于Adams-4需要RK-4提供启动条件,而RK-4方法迭代次数l=3,完成3次迭代后,其提供的启动条件为y3、z3、t3、z、z1、z2、f(0)、f(1)、f(2),对比Adams-4的启动条件发现,缺少f(3)。因此,如果采用折叠因子N=2的折叠结构求解空间运动方程,那么其折叠集需要进行优化和重映射,将启动条件f(3)的计算也包含在折叠集中。通过对式(5)的递推关系进行拆分和重定,同时将SMECU求解f的运算任务在折叠集任务中的相对位置进行调整,求解得到的DFG如图3所示。

图3 Adams-4方法折叠结构下优化的DFG

根据RK-4、Adam-4的折叠集,结合2种数值求解方法在求解空间运动方程时的工作模式,即可得到2种方法在ACU中的总折叠集为{SM,SA},其中,折叠子集SM={SM1,SM2,SM3,SM4};SA={SA1,SA2}。2个折叠子集对应重定时的关系见表1所列。

表1 RK-4、Adams-4方法折叠集相互关系

表1中,折叠子集SM的迭代次数为3,即迭代3次后即可结束当前子集,开始运算子集SA;但2个折叠子集对应的折叠因子N不同,因此在计算执行时刻时,需要添加约束条[4l1+3,2l2],即时刻4l1+3和时刻2l2属于相邻时刻,才能保证重定时后的执行时刻符合折叠子集运算规律。

由图2、图3可知,在2种方法折叠结构所需的功能单元中,SMECU为同一单元,而2个DFG中ACU功能单元所承担的运算任务复杂度不同,对2个DFG中ACU功能单元所需的运算器数量进行统计,得到运算器数量的统计结果,见表2所列。

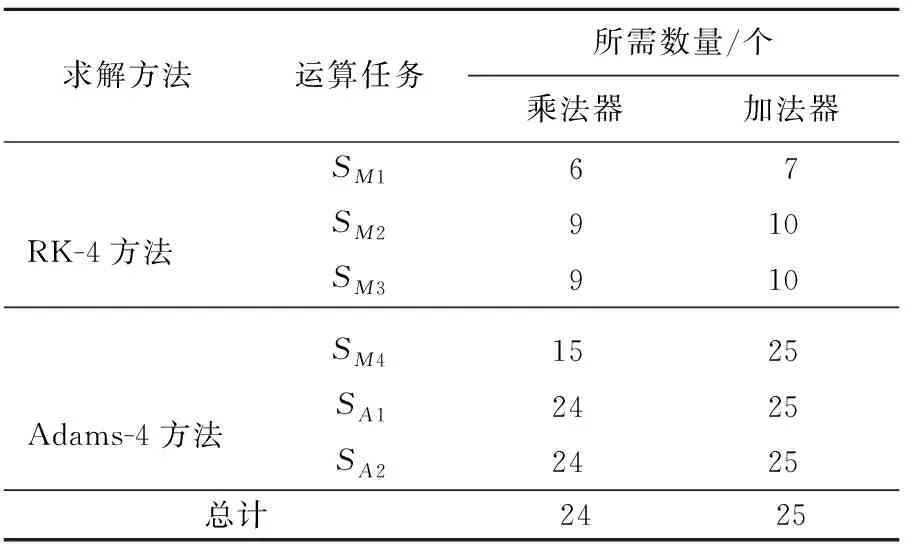
表2 RK-4、Adams-4方法折叠结果运算器数量统计

因为Adams-4预测校正方法对ACU功能单元内的运算器需求量更大,所以在考虑运算器复用后,ACU功能单元由24个乘法器和25个加法器组成。根据上述ACU基本运算器组成方案,结合图2、图3所示的DFG,即可分别得到RK-4和Adam-4不同折叠任务所需的运算器链接关系。

为了求得2种方法对ACU中运算器链接关系的最小并集,将RK-4方法每个运算任务下的链接关系依次映射到Adams-4方法下的运算器链接关系中,通过对所有情况的并集进行比较,得到最小并集,并根据最小并集完成ACU中运算器链接关系的配置,得到数据路径动态配置方案,如图4所示。

图4 RK-4、Adams-4方法融合工作的数据路径动态配置方案

参考表1的任务标号和执行时刻,根据迭代次数得到ACU中任务执行顺序,设计SM的控制结构,通过实时检测任务执行过程实现任务状态的精准、动态切换。

SMECU根据ACU提供的函数f的输入,完成函数值的计算,即SME方程值的计算,并将结果返回ACU。

参考式(1)及文献[1]的相关结论,选择流水线计算模式的加/减法器、乘法器、除法器、三角函数运算器等运算单元,采用管道结构对SMECU进行设计;分析SME中多个运算链之间的依赖关系,对部分运算单元的Latency进行动态拉伸,避免数据缓存对存储器的访问。SMECU所设计的管道深度为260,具备流水工作特征能够准确批量地计算SME的方程值。

3 实验分析与性能测试

本节针对SMEFS的运算模式和功能,选取多种应用场景下的2 600组运算任务,本文对SMEFS的求解速度及求解结果进行测试验证。结合批量求解任务的求解速度、求解结果相对误差分析以及部分运算任务的运算过程进行对比分析,充分证明该求解器的高效性、功能完备性及可靠性。

为更好地测试系统的峰值性能,实验选择的测试集包含10个运算任务,每个任务包括260组初值。为了尽可能贴合实际应用测试硬件的性能,所选的10个运算任务的迭代次数在30 000～50 000之间不等;每个运算任务内的260组初值的迭代次数极差在1 000以内。

3.1 实验环境

软件实现的载体是飞腾D2000 CPU @ 2.60 GHz,32 GiB DDR4 2 800内存,Ubuntu18.04 64位操作系统的PC,使用GCC 7.3.0编译环境和C语言编程工具,采用与快速求解器同样的求解方法和数据格式,对空间运动方程进行求解,硬件平台采用Xilinx Vivado 2018.3作为开发工具,以Xilinx公司Virtex-7 XC7V690TFFG-2型FPGA作为SMEFS实现的载体,FPGA芯片最高资源利用率为60.7%,系统工作主频为150 MHz。实验使用MATLAB完成图像及数据精度对比等操作。

3.2 加速比测试

加速比测试实验主要测试空间运动方程快速求解器完成批量初值的空间运动方程求解任务相对于软件的加速比。将测试集的初值分别在PC、FPGA上完成求解,并分别记录软硬件的计算耗时,依次统计软硬件计算完成10个任务的运算耗时和加速比,结果见表3所列。

表3 软硬件求解五自由度SME计算耗时对比

对表3中10个任务的加速比求平均值,可以得到硬件求解相对于软件计算的平均加速比为12.765。

3.3 精度及误差测试

从10个任务中各抽取2组初值,绘制软硬件求解得到的弹道并进行对比,初步判断计算结果的精度。对2 600组初值最后一次迭代的结果进行相对误差分析,进一步判断误差范围。通过MATLAB对20组软硬件计算结果绘制图像,为直观对比图像误差,将空间直角坐标系o-xyz投影到平面坐标系xoy上,得到弹道对比结果,如图5所示。从图5可以看出,软硬件求解的弹道几乎完全重合。

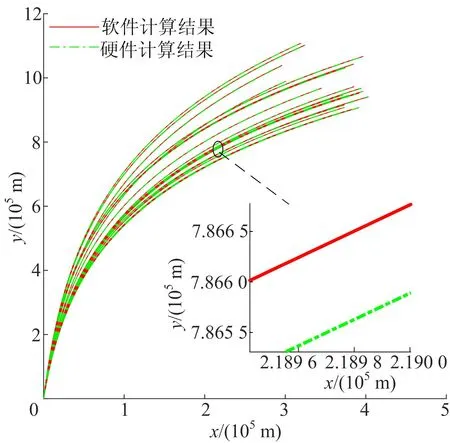
图5 SME软硬件求解结果对比

2 600组初值的计算结果中,包括位移向量(x,y,z)和速度向量(vx,vy,vz),参考绘制图像的做法对位移量进行分析,仅对x、y进行误差分析;而对速度量的分析是将软硬件求解的速度矢量求模,并对速度的模值进行误差分析。借助MATLAB绘制3组变量的相对误差散点图,如图6所示。

图6 变量x、y、v的软硬件计算结果相对误差散点图

由图6可知：x的相对误差均小于9×10-6;y的相对误差均小于9×10-5,误差较小;v的相对误差均小于9×10-4,该变量的相对误差较大,原因是速度通过向量模值进行误差分析,存在3个变量误差累积的现象,因此误差高出一个数量级属于理论范围,实际计算结果(vx,vy,vz)的相对误差仍可达到10-5数量级。

4 结 论

针对发射坐标系下五自由度空间运动方程的快速求解问题,选择求解速度更快的RK-4方法和Adams-4方法相结合的数值求解方法,采用折叠技术和管道式设计结构,在给定的资源上设计一种空间运动方程快速求解器,实现对实际应用中空间运动方程大批量求解任务的有效加速。基于FPGA的快速求解器验证实验表明,在大批量求解任务中,SMEFS相对于国产CPU的平均加速比为12.765,且硬件求解与软件求解的相对误差小于9×10-5,具备较大的速度优势和较高的计算可靠性。