基于K-means聚类分析和多元线性回归的相关流量数据处理方法*
2024-01-30张李娜姜志诚刘大勇刘兴斌
张李娜,姜志诚,刘大勇,刘兴斌
(1.东北石油大学 黑龙江 大庆 163318; 2.中国石油集团测井有限公司华北分公司 河北 任丘 062552)
0 引 言
相关流量计在油田油气水地面计量[1]和油井产出剖面测量中得到了成功的应用。相关流量计的测量原理是利用流体内部存在扰动“噪声”,采集上、下游传感器输出的对含水率敏感的随机信号,对两路信号进行处理,滤去直流信号和高频噪声,从而获得上游传感器和下游传感器的随机流动噪声信号x(t)和y(t)。在满足流体“凝固”模型条件的前提下,两路传感器所输出的流动噪声信号波形相似,但在时间上有一个延迟τ0。将两个信号进行互相关运算,可得到互相关函数Rxy(τ)。
Rxy(τ)的峰值所对应的时间轴位置即τ0,为流体从一个传感器到另一个传感器所用的时间,称为渡越时间(Transit Time)[2]。相关流量法是建立在理想流动状态条件下,在实际应用中,尚有不少干扰检测的问题必须注意。首先,装设于测量管道上检测流体噪声的传感器一般都具有类似的几何特征,它对被测的混合流体流动产生的随机噪声信号有一定的空间滤波作用,不同相流体之间有一定程度的滑脱现象,这就使得检测得到的随机噪动信号的渡越时间出现偏差;其次,流体在流动过程中,流体不同相的分布会有一定程度变化,导致上游、下游两路随机信号的随机流动噪声信号波形的相似度降低[3];第三,信噪比也是一个影响相关流量测量精度的重要因素,如果有效信号幅度变小则信噪比变低,导致流动信号特征不明显。以上因素都会使检测得到的两路随机噪动信号的渡越时间出现偏差,造成互相关法得到的流量出现较大的测量误差。
针对两相流参数测量问题,一些学者提出极性导向式自适应算法[4]、参数估计法[5]等方法,但对渡越时间的异常值未发现有相应的修正方法。多元线性回归方法和聚类分析的预测方法具有模型简单、计算精确、模型解释能力强等优点[6-8]。对此,张裕[9]等提出了一种基于K-means聚类算法的多元线性回归模型预测台区线损率方法,利用K-means对台区数据进行了合理化分类,并建立了有效的回归预测模型。因此,为实现渡越时间数据由全局最优转为局部最优,提高模型预测性能,利用K-means聚类算法对渡越时间样本数据聚类分析[10-11]。该方法是一种基本的划分方法,主要优点是算法简单、快速而且能有效处理大数据集[12]。本文将多元线性回归方法与K-means聚类算法相结合,应用于相关流量计异常数据的处理,经多相流实验装置得到的实验数据验证,该方法是有效的。
1 数据预处理
渡越时间数据是时间序列,异常情况主要分为单点数据异常和多点数据异常。异常数据检测的基本目的,就是识别离群度较高的数据点,针对不同的异常情况进行检测识别并修正。数据预处理流程如图1所示。
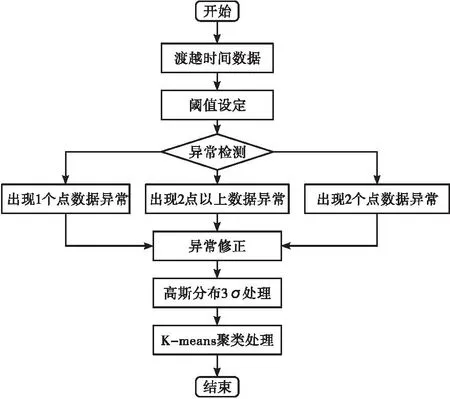
图1 数据预处理流程图
正常情况下渡越时间波动性很小,不会发生显著跳跃变化。渡越时间的有效范围约为0.001~1 s之间,根据这一特征将0.001 s、1 s判定为阈值的上下界限,将阈值外的数据判定为异常情况。为进一步保障序列的平稳性,通过高斯分布的3σ准则进一步判定数据异常情况。3σ准则又称为标准差法,标准差是反映一组数据离散程度最常用的一种量化形式,是表示精确度的重要指标。在正态分布的假设下,数值X距离平均值μ三倍标准差之外的出现概率很小,因此可以认为是异常值,距离平均值3σ之外的值出现的概率为:
P(|X-μ|>3σ)≤0.003
(1)
渡越时间数据异常识别后,须对异常数据进行修正。异常数据段异常数量为1个或2个时,采用均值替换;异常数据段异常数量大于等于3个时,则采用非局部相似数据段均值替换。1个数据异常情况时,用异常值前后有效数据段求和取均值替换;2个连续数据异常时,第1位异常值用左邻域有效数据段求和取均值替换,第2位用其右邻域有效数据段求和取均值替换;数据段缺失值数量大于等于3个时,采用非局部相似有效数据段均值替换。具体操作步骤为筛选与当前异常数据段结构相似的所有数据段,将其定义为参考数据段,计算异常数据段与参考数据段之间的相关系数,按由大到小顺序取相关性最强的3组参考数据段,3组参考数据段求和取均值并与异常数据段相应位置完成替换。为保证均值填充过程中左右邻域都存在有效数据,在数据开头、结尾处须判断有无异常情况,若判定为真,需将第一个或最后一个有效值添加到数据的开头或结尾位置。
渡越时间数据不会单趋势地递增或递减,利用K-means聚类算法将渡越时间样本数据分为K类,将渡越时间以全局最优转为局部最优,K-means聚类算法的主要流程如下:
1)随机指派K个数据点作为算法的初始聚类中心,即初始类簇中心a=a1,a2,…ai;
2)然后,计算数据集中所有样本点xi到它的K个聚类中心的最短距离,把所有样本数据划分到与其最相近的中心点所属类簇;
3)对调整后的类簇重新计算其簇中心,再次依据相似度更新所有点的所属簇;
4)如此反复迭代,直至聚类准则函数收敛或达到迭代次数。
在该算法中,采用欧氏距离(见式(2))作为数据点之间的相似度。
(2)
其中,D是代表样本与聚类中心之间的最短距离,xi代表第i个样本值,而ai代表簇对应的中心点,M则表示是样本总量。根据K-means聚类算法对渡越时间数据的聚类结果,建立多元线性回归模型。
2 预测模型建立
模型预测形式为用每6个历史数据来预测第7个数据。每帧渡越时间共计120个,将已知120个实验数据通过逐列循环移位的形式构成一个120×7的矩阵,矩阵定义为R,第7列定义为因变量y,前6列定义为自变量xi,j(i=1,2,3...120;j=1,2,…,6)。
设因变量y与自变量xi,j满足如下线性关系:
y=α0+α1x1+α2x2+…+α6x6+ε
(3)
y受到6个非随机因素x1,x2,…,x6和随机因素ε的影响。其中α是6个未知参数,ε是服从标准正态分布的随机变量,称为误差项。对于120行数据样本:
(4)
其中ε1,ε2,...,ε120相互独立,且服从ε~N(0,δ2)分布。
其中:
(5)
(6)
(7)
(8)
将式(4)用矩阵形式表示
Y=XA+E
(9)
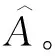
(10)

(11)
3 算例分析
选取4帧相关流量计在多相流装置中所测得的实验数据,对每帧渡越时间样本数据分别进行处理。每帧120个数据,分别建立4组预测模型,称为模型1、模型2、模型3、模型4,并分析预测模型效果。将数据导入MATLAB计算程序,通过plot函数绘制渡越时间散点图。
应用上文提出的数据预处理方法对4帧渡越时间数据进行异常检测,如图2所示。

图2 异常检测后4帧渡越时间散点图
图2中分别展示了4帧渡越时间数据的散点图,纵坐标表示渡越时间(τ),横坐标表示渡越时间的时间序列,红色数据表示为有效数据,蓝色数据表示为异常数据。图2清晰显示,异常数据与有效数据之间存在较大的偏差,异常数据值波动范围较大,分布不均,误差率为4%~5%。为保障后续流量值的准确性,根据经验设定阈值区间,渡越时间样本数值大于等于1 s或小于等于0 s 则判定为异常值。判断出所有样本中异常数据,通过均值修正和非局部相似数据段均值修正,再通过高斯函数3σ准则处理得到结果如图3所示。
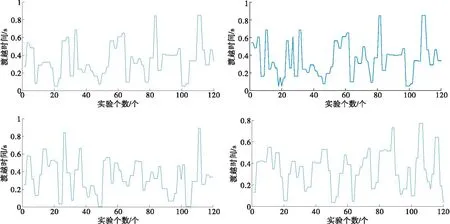
图3 数据预处理后4帧渡越时间数据
图3中表示数据预处理后的数据波动情况,可直观看出4帧数据中均无阈值外的异常数据点,异常数据点已都被完全替换,并保持数据稳定在0~0.9 s之间。基于上文预测模型的建立,分别对每一类数据集建立多元线性回归方程及决策树。4帧数据聚类后的3类多元线性回归模型参数及R2信息见表1~4。特征参数为式(4)中的α,R2为决定系数,表征拟合的程度。

表1 第1帧数据参数值

表2 第2帧数据参数值

表3 第3帧数据参数值

表4 第4帧数据参数值
以上为4帧数据的回归模型参数汇总,显示了每帧数据回归模型的参数情况以及决定系数R2,从运算结果上看,R2基本满足拟合要求。每帧数据决定系数的平均值均可达到0.5,此模型可作为渡越时间预测模型使用。
根据上述模型建立分析结果,导入新一帧数据集,并将含有异常值的渡越时间数据进行数据预处理,将预处理后数据集定义为Testdata,如图4所示

图4 新一帧数据预处理前后渡越时间数据对比
由图4可以看出,数据预处理效果明显,异常数据都已完成替换。因上文4个模型所得数据都在可靠范围内,此处选用模型1,将模型1中数据预处理后定义为Traindata_1。将数据集Testdata导入已建立的模型1中,得到预测曲线,并将预测数据集定义为Prodata,如图5所示。

图5 Prodata与Testdata对比
图5中蓝色曲线代表Prodata,红色曲线为Testdata。因前6个数据值是作为历史数据,所以Prodata预测值从第7个数值点开始,并依次往后递推。从图中可清晰看出,预测曲线围绕实测值在一定范围内上下浮动,经计算,预测值与实际值之间有90%的差距在[0.3,-0.3]之间,因此可以将预测值作为修正异常值使用。
将数据集Testdata与Prodata加以判断得到最终处理结果,判断过程为:若Testdata(k)满足合理区间范围,则输出Testdata(k),否则输出Prodata(k);k=1,2,…,120。Testdata(k)表示数据集Testdata中的第k个数据点,Prodata(k)表示数据集Prodata中的第k个数据点,最终预测值与实际值判断后输出结果如图6所示
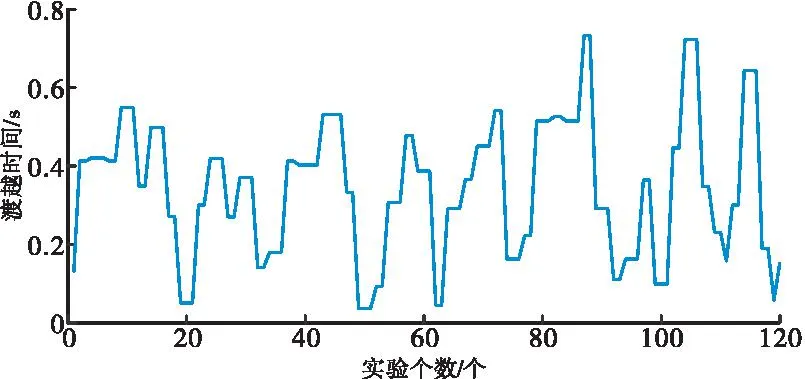
图6 最终输出数据
4 结 论
本文针对相关流量法测量流量存在较大误差现象,提出了有效识别并处理渡越时间样本中的异常数据的方法,得出以下结论。
1)通过应用阈值法、均值替换法和非局部相似均值替换法,对数据进行处理后,效果显著。可以完全替换数据集中的大误差数据,异常率从4%~5%降至1%以内,增强了数据的可靠性。
2)多相流装置中获得的相关流量计的测量数据证实,基于K-means聚类分析和多元线性回归分析预测后,预测值与实际值之间有90%的差距在[0.3,-0.3]之间,这说明预测值与实际值之间有很高的匹配度,预测结果可以用来替换渡越时间数据集中的异常值,验证了模型的有效性。
上述工作证实了基于K-means聚类分析和多元线性回归的相关流量数据处理方法的可行性,为下一步工程设计提供了指导。
