地铁盾构施工过程中底部管片的上浮机制研究

2024-01-30杨鑫汪邝利军于广明张树光白丽扬

现代城市轨道交通 2024年1期

杨鑫汪，雷军，邝利军，于广明，张树光，白丽扬

（1.青岛理工大学土木工程学院，山东青岛 266400；2.中国建筑第五工程局有限公司，湖南长沙 410007；3.桂林理工大学土木工程学院，广西桂林 541000）

1 研究背景

随着我国经济快速发展，城市人口密度与日俱增，城市交通拥堵成为各大城市治理难点[1]。地铁由于其高效准时、绿色环保、节约地面空间等优势，成为各大城市公共交通的重要组成部分。随着我国隧道建设的施工方法不断改进优化，盾构法因其对附近既有建（构）筑物的影响较小，施工建设安全高效，已被广泛应用于各大城市的地铁建设。但由于施工过程中地层性质限制和施工技术水平有限，盾构隧道管片衬砌的上浮问题已经成为盾构施工领域亟待解决的工程问题。目前，国内外学者对于盾构法施工中管片结构的上浮都已经进行了深入的研究，普遍认为这种现象是由于围岩应力释放与注浆浆液产生的浮力应力协同造成的。针对盾构施工过程中管片上浮问题的研究方法主要分为两大类：一类是以数值模拟和现场监测试验相结合的研究方法；另一类是运用理论分析建立上浮计算模型的研究方法。DO[2]等通过FLAC 3D 软件对盾构开挖的过程进行精细化模拟，通过计算分析可知注浆压力和顶推力对衬砌结构受力有很大影响。傅鹤林等[3]建立有限元模型对某盾构施工过程进行模拟，考虑渗流场、隧道埋深及注浆压力等因素对管片不同部位的上浮影响。上述研究主要基于工程实践和现场实验对管片上浮机制进行数值模拟，总结了影响管片上浮的因素。叶飞[4]等对盾构施工管片相邻环间接头及覆土荷载产生抗浮作用进行研究，考虑纵向螺栓预应力、顶推残余应力产生的摩阻力和上覆土荷载推导出盾构隧道的抗浮计算公式，并通过工程实例验证。魏纲[5]等通过运用Maag 球面扩散理论建立管片的压力公式对上浮管片进行分析，并以此提出单环管片受力计算模型和公式。张雨帆[6]将单块管片上浮定义为管片受到动态上浮力，考虑环向螺栓的抗剪作用以及纵缝摩擦阻力，未考虑上覆土荷载的抗浮效应。杨志勇[7]等对注浆后的管片进行受力分析，推导出管片受力公式并运用Matlab 数值拟合建立管片上浮量解析解，结合工程对公式进行验证。上述研究主要通过理论推导建立了各种力学简化模型，并对管片上浮机理进行探讨。综上所述，针对管片上浮问题的研究主要集中在整体管片结构和单环管片的力学分析，而对于单块管片的上浮机制研究较少，因此有必要对单块管片关于上浮力的解析解进行更深入的研究。

本文主要运用理论解析的研究方法，基于现有研究对盾构管片衬砌结构底部管片在不同施工阶段的上浮原因进行分析，建立同步注浆阶段的底部管片衬砌力学简化模型，利用分离变量法推导出单管片上浮量的计算公式，并根据施工现场情况提出相应的控制措施，底部管片的上浮研究如图1 所示。

2 管片上浮原因探讨

盾构施工过程中，管片结构上浮的原因有很多，一方面由于盾构掘进过程中超挖间隙过大、盾构施工姿态偏移、注浆压力的差异导致管片结构受力不平衡；另一方面，管片的上浮与注浆材料及盾构施工所处的地质环境等因素有关[8]。针对盾构施工管片上浮问题，相关研究者[9-10]对其上浮原因总结为：①盾尾间隙注浆后，浆液包裹管片为其提供了静态上浮力；②管片因注浆压力而产生动态上浮力；③上覆软土对管片结构的反向压缩；④千斤顶顶推时，因管片受力不均匀产生偏心荷载；⑤ 盾构隧道上方开挖对其管片结构产生卸荷作用。

本文依托深圳地铁13 号线留仙洞站—百旺港大站区间工程对底部单块管片的上浮现象进行研究，管片衬砌构造如图2 所示，分别由B1T、B2T、B3T 标准块和L1T、L2T 相邻块，外加FT 封顶块构成。本文主要对底部管片（B2T）在盾构施工不同阶段下的受力状态进行受力分析，并依据管片在盾构施工的不同阶段对其上浮阶段进行划分。

图2 深圳地铁13 号线管片衬砌构造图

2.1 底部管片（B2T）在拼装阶段的上浮

盾构机在掘进开挖岩土体时导致其前方岩土体被卸载，同时盾构机的自重又反作用于地层，但已开挖岩土体堆积在土仓内，导致盾构机前盾重力相对较大[11]。此外，盾构机头部由于有刀盘相较于盾尾质量更大，故在静力平衡作用下盾构机会出现“磕头”现象，即盾构机的盾尾发生上翘。

盾壳作用下管片上浮示意如图3 所示，在盾构机还未发生偏转时，脱出盾尾的管片在千斤顶顶推作用下正常被推出盾尾，管片不发生上浮。但是，当盾构机在下坡段进行掘进需要纠偏时，盾构机前方地层土体被卸荷，土仓内堆积渣土时，盾构机机头部分在重力的作用下会发生偏离轴线的位移。

图3 盾壳作用下管片上浮示意图

2.2 底部管片（B2T）顶推时的上浮

千斤顶是盾构机持续推进的主要力源，其通过顶推杆直接作用在管片上，以拼装完成的最近一环管片为支撑，为盾构机提供向前掘进的动力。千斤顶压力对管片影响较大，管片端面如有凹凸不平，在顶推时极易发生剥落、破损。当千斤顶压力合力不与管片端面垂直时，就会使隧道产生纵向的弯矩，造成环间连接处开口，从而使盾构隧道出现浆漏。同时，施工时衬砌纵向变形刚度受千斤顶压力影响较大，在盾构掘进施工中，管片在轴线方向发生弯曲变形，可能会受到偏心荷载作用[12]。

千斤顶顶推时B2T 管片受力如图4 所示，盾构机向前掘进顶推时，液压千斤顶会给底部管片（B2T）施加一个与掘进方向相反的作用力F1。当F1与y轴方向形成夹角时，底部管片的重力和管片之间作用力不足以平衡其在z轴方向的分力时，管片结构发生移动从而引起上浮及错台等现象。

图4 千斤顶顶推时B2T 管片受力立体图

为了更具体地说明B2T 管片受偏心荷载作用时的受力状态，当时，千斤顶的推力和管片的重力相互平衡，不会发生管片上浮或错台现象，其中F1在y轴方向形成夹角为θ。但当时，则B2T 管片会产生竖直方向的位移，导致底部管片（B2T）出现上浮。G为管片的自重，其计算式如下：

式（1）中，γc为管片容重；b为管片环宽；R0为管片外径；R1为管片内径；n为管片所对应的圆心角。

2.3 底部管片（B2T）脱出盾尾后的上浮

随着盾构机的持续推进，已完成拼装的管片逐渐脱离盾尾，由于掘进隧道外径稍大于管片外径，因此在隧道与管片环之间产生环形间隙。为了使脱出的管片结构获得周围岩土体的支撑，确保管片结构初期稳定从而提高隧道的抗渗性，预防盾构隧道上方地表发生沉降，故需对这部分间隙进行注浆填充。

管片脱出盾尾受力示意如图5 所示，管片结构处于软岩层，需考虑管片上覆软岩的荷载作用W，若Ff＞G+W，即在管片与上覆土重力之和（G+W）比浮力（Ff）小的情况下，底部管片所在的衬砌结构有上浮的趋势。当盾构隧道处于硬质岩层中时，由于管片衬砌受围岩压力较小，此时隧道管片衬砌上方岩土体对管片产生的上覆软岩的荷载作用也较小。管片脱离盾尾后，其盾尾间隙可能在很长一段时间内存在。此时，对盾尾间隙进行注浆处理。在此时若注浆浆液产生的上浮力Ff＞G，则管片有上浮趋势[13]。

图5 管片脱出盾尾受力示意图

2.4 浆液初凝后的底部管片（B2T）的上浮

由于注浆材料的差异性，盾构机尾部间隙空间的复杂性，注浆浆液在盾尾间隙中逐渐凝固的过程是浆液压力逐渐减弱直至消失的非常复杂的物理-化学变化过程。影响浆液初凝的因素较为复杂，主要与同步注浆配比及浆液性质、地层特性以及包括盾构掘进速度、盾构推力、注浆压力等在内的施工参数有关[14]。

3 底部管片（B2T）上浮受力简化模型

由前文的底部管片上浮原因分析可知，管片在不同的施工阶段出现上浮的原因也不同，在上浮受力模型建立时，本文仅对底部管片脱出时的受力进行分析（图6），由于管片的上浮过程相对于整个施工期其上浮时间较长且速率很小，故假设底部管片在整个施工期的上浮处于一个力学平衡状态，只分析其在上浮运动方向上的位移。

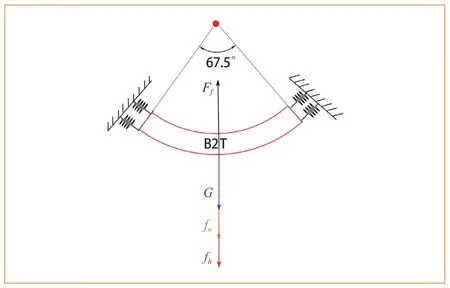
图6 B2T 管片受力简化图

底部管片与相邻管片之间的相互作用力等效为抗剪弹簧，分析当B2T 管片受到上浮力时与相邻管片之间的作用力：

式（2）中，Ff为管片在浆液中受到的上浮力；G为B2T管片的自重；fn为B2T 管片在注浆浆液中受到的粘滞阻力；fh为B2T 管片与相邻管片之间的环间摩擦阻力。由于单块管片的上浮为局部上浮，分析单块管片的上浮机制时，主要考虑环向螺栓的阻力以及纵缝的粘滞阻力，不考虑上覆土的抗浮效应。本文主要研究影响底部管片（B2T）上浮的几种主要力的平衡关系，通过理论分析依次推导上浮力、相邻环间阻力、浆液对管片外壁的粘滞阻力以及管片自重的理论计算方法，并依此分析B2T 管片上浮受力简化模型，推导其上浮量计算公式。

3.1 底部管片（B2T）管片上浮力计算

由前文对管片上浮原因分析可知，管片结构注浆浆液中受到的浮力主要来自以下2 种，其一是由未凝固的浆液和地下水的混合液裹挟管片产生的静态上浮力，其二是注浆压力产生的动态上浮力。

在静态上浮力分析计算时，若不考虑地下水对管片上浮力的影响，则直接取计算容重为注浆材料的容重；若考虑地下水对其上浮力的影响时，其计算容重应根据地下水对浆液的稀释程度，计算其与注浆材料的比例，根据比例推算混合浆液的容重，充分考虑地下水对注浆材料有稀释作用，合理计算静态上浮力，其计算表达式如下：

式（3）中，n为底部单块管片对应的圆心角；b为底部单块管片环宽；R0为管片外径；γj为包裹管片的浆液容重。

在动态上浮力计算时，由于管片所处的围岩环境和注浆压力不同，对动态上浮力的计算结果具有显著的差异。BEZUIJEN A.等[15]进行了注浆压力对盾构管片上浮影响的研究，其研究结果表明，注浆压力对管片的影响范围有限（2～3 环），注浆压力在管片横断面上呈线性分布，其大小及在横断面上的分布梯度随盾构掘进的推进而逐渐衰减，最后逐渐降低到与围岩静水压力相同。若当注浆的扩散方式为压密注浆时，注浆浆液由于重力的作用，会顺着管片衬砌在管片结构的底部聚集，形成管片上浮的动态上浮力[16]。因此本文假定横断面上注浆压力随深度线性变化，且注浆压力随着浆液凝固沿轴线线性减小，浆液初凝位置与周围地层的水土压力相同。

严密注浆下浆液压力分布如图7 所示，由注浆压力引起的动态上浮力为[10]：

图7 B2T 管片受力简化图

本文仅对底部管片（B2T）进行分析，即当其产生最大动态上浮力时的状态进行讨论，取θ=33.75°。

式（4）～式（5）中，b为管片环宽；p为注浆压力；R0为管片外径；α为动态注浆浆液对应的圆心角；θ为X轴与底部管片浆液分布区边界夹角。

3.2 底部管片（B2T）环间阻力的计算

管片环间阻力主要由2 部分组成：①由于千斤顶推导致相邻管片间接触并挤压产生的滑动摩擦力；②由连接管片之间的螺栓产生的抗剪作用力。BILOTTA E.等[17]对意大利那不勒斯土压平衡盾构隧道预制管片衬砌两端的应变进行长期监测，其研究结果表明：螺栓抗剪作用对管片两端的应力变化影响不大。因此本文对底部单块管片的上浮量进行分析，环间阻力仅考虑螺栓预紧力和管片环间滑动摩擦力。

环间摩擦阻力按下式计算：

式（6）中，μ为环间活动摩擦系数，取值为0.3；Nh为环间的接触压力。

Nh主要由螺栓预紧力和盾构机千斤顶顶推产生的残余应力组成，故可将上式改写为：

式（7）中，Ni为单个螺栓预紧力；Nj为千斤顶顶推压力；n为管片上的螺栓数。根据戴志仁[18]的研究结果可知，为综合考虑力的传递衰减作用和施工安全，Nj取值为N总的15%，且为方便计算假设总顶推力沿管片接触环面平均分布，取Nj＝0.15N总。

3.3 底部管片（B2T）粘滞阻力的计算

根据浆液的水灰比（W/C）不同可将浆液分为3 种流型，分别是幂律流体（W/C=0.5～0.7）、宾汉流体（W/C=0.8～1.0）、牛顿流体（W/C≥ 2.0）。根据现场对注浆材料进行测定，深圳地铁13 号线留仙洞站—百旺港大站盾构区间注浆浆液W/C=2.0，可判定其流型为牛顿流体。由于管片与围岩间的间隙相对较小，浆液在这部分狭小空间流动，符合牛顿内摩擦定律的条件，因此将其流动速度τ假设为线性分布[19]。

其中，切向流速vq与管片上浮速度v满足下列公式：

管片上浮所受的粘滞阻力为：

其中，牛顿流体黏度时变性规律可运用指数函数拟合为：

式（8）～式（11）中，δ为未注浆管片与围岩间距离；μt为注浆浆液的黏度；k1、k2分别为注浆材料黏度时变性参数；t为管片注浆后上浮时间。

3.4 底部管片（B2T）上浮量计算

将公式（1）、公式（7）、公式（10）、公式（11）代入公式（2）中得到：

对公式（10）进行分离变量法积分可以推导出：

当t=0 时，上浮量s=0，作为边界条件代入公式（13），求出公式中的常系数为：

故B2T 管片的上浮量为：

4 工程实例分析

4.1 工程概况

深圳市地铁13 号线留仙洞站—百旺港大站区间盾构隧道洞径约6.7 m，埋深为30.5 m，隧道平面布置图如图8 所示，全长为4 610.855 m，采用盾构法施工，区间线路最大线路纵坡28.0‰，最小纵坡为2‰。

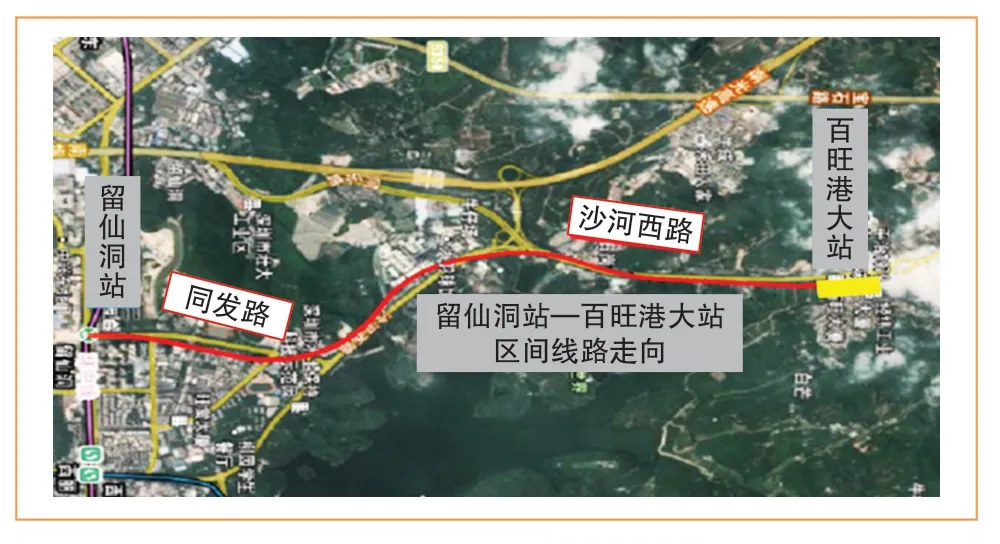
图8 留仙洞站—百旺港大站区间隧道平面布置图

区间穿越的地层情况复杂多变且分布不均，地基土上部以素填土、淤泥质黏土、粉质黏土和沙土为主。下部地层以全风化花岗岩和混合花岗岩为主，局部穿越硬塑砾质黏性土、全-强风化黑云母花岗岩、全-强风化混合花岗岩、微风化花岗岩，全线地质条件如图9 所示。

深圳地铁13 号线管片基本设计参数如表1 所示，注浆浆液配合比如表2 所示，注浆材料的基本参数如表3 所示。

表2 注浆浆液配合比

表3 注浆材料基本参数

4.2 底部管片（B2T）上浮量的影响因素探讨

根据推导出的上浮量计算公式可以计算出单管片在注浆阶段的上浮量，也可发现影响单块上浮量的因素包括注浆压力、注浆浆液水胶比、动态上浮力、螺栓预紧力和盾尾间隙等。本节主要考虑不同注浆压力以及不同注浆水胶比对单管片上浮量的影响规律。

4.2.1 注浆压力对底部管片（B2T）上浮的影响

依据深圳地铁13 号线留仙洞站—百旺港大站区间盾构施工相关实测数据可知，注浆压力随盾构机的推进不断变化，注浆压力在2.5～7.5 bar 之间进行动态调整，故取盾尾间隙为0.1 m，环间摩擦系数为0.15，螺栓预紧力为120 kN，管片上共有纵向螺栓6 根，浆液水胶比约为0.9，黏度时变性系数k1为9 MPa·s，k2为0.02 min，其余管片参数参照表1。依据上述各项参数代入公式（15）可以绘制出不同注浆压力下上浮量与时间的关系图，如图10 所示。

图10 不同注浆压力下上浮量与时间关系

由图10 可知，单块管片的上浮量随着上浮期时间的增长逐渐增大，最终趋于稳定。将单块管片的上浮分为3 个阶段：Ⅰ阶段为管片上浮的线性发展阶段，主要发生在上浮期的前2 h；Ⅱ 阶段为管片上浮的圆弧发展阶段，相较于Ⅰ阶段，上浮速度逐渐减缓，主要发生在2.5～10 h；Ⅲ 阶段为管片的上浮稳定阶段，随着浆液的逐渐凝固，作用在管片上的上浮力逐渐减小，地层对管片衬砌结构的约束逐渐增强，管片上浮逐渐趋于稳定状态，主要发生在10 h 以后的阶段，与表3 中的注浆浆液凝结时间基本吻合。上述管片上浮的3 个发展阶段界限比较明显，基本符合现场管片上浮发展规律。在不同的注浆压力作用下，单块管片的上浮量也不同，当注浆压力为7 bar 时，产生的上浮量最大，所以通过控制注浆压力可以有效的抑制单块管片的上浮。

4.2.2 注浆材料对底部管片（B2T）的上浮影响

由于注浆材料其水胶比不同，对应的流型也不同，且流型相同的浆液其水胶比对管片的上浮量影响也不同。本研究主要通过控制注浆材料的水胶比，分析管片的上浮变化。在注浆压力为3 bar 时，分别取水胶比为0.8、0.9、1.0 的注浆材料分别进行计算。不同水胶比下的黏度时变性系数参照表如表4 所示。

表4 不同水胶比下的黏度时变性参数

依据表4 所给参数和盾构掘进相关参数代入公式（15），可以计算出单块管片的上浮量，绘制出不同水胶比下的单块管片上浮量与时间的关系图，如图11 所示。

图11 不同水胶比下单管片上浮量与时间的关系

由图11 可知，随着水胶比的增大，单块管片的上浮量也逐渐增大，这是因为随着水胶比的增大，注浆材料中的水泥和粉煤灰的掺量相对减少，浆液的黏度也随之减少，浆液的初凝时间增大，浆液提供的动态上浮力增大，上浮量也随之增大，所以通过控制注浆材料的水胶比可以有效的控制管片的上浮。

5 管片上浮控制措施

5.1 注浆压力的控制

由前文分析计算结果可知，不同的注浆压力会产生不同的动态上浮力，由于底部管片相较于整环管片是最先被注浆浆液的裹挟而产生静态上浮力的衬砌结构。因此当底部管片因受到静态上浮力而有上浮现象出现的趋势时，应增加顶部注浆孔的注浆压力同时适当减小底部注浆压力，从而起到依靠动态上浮力抵消一部分静态上浮力，通过对注浆压力进行实时调控以达到抑制管片上浮的效果。但是，在对注浆压力进行实时调控的同时应时刻监测盾构隧道上方地表沉降值，防止因减小注浆压力而导致隧道围岩不能及时被管片结构支护，影响地表建（构）筑物安全。

5.2 注浆浆液的水胶比控制

由前文分析结果可知，注浆浆液的特性在施工阶段中对控制管片上浮量起关键作用，通过控制浆液的水胶比可有效控制管片的上浮量。由于浆液的早期抗剪强度越高，触变性越大，抵抗上浮的能力也越好。为了使管片结构初期形成支护，可以调整粉煤灰的比例或适当增加速凝剂来降低其的塌落度及流动性等材料特性。在富水硬岩地层中采用速凝型单浆液，抗水分散性好，可实现减少浆液初凝时间，从而控制盾构管片衬砌上浮。

5.3 底部管片上覆质量控制

在管片结构的内部增加一定质量的重物是最经济且最有效的物理抗浮措施，根据底部管片上浮量计算公式可知，在管片结构内部增加重量，相当于增加了管片的自重。在浆液还没完全凝固时，浆液还处于牛顿流体状态其还可以为底部管片提供静态上浮力，此时增加管片的自重可以抵消一部分上浮力。但是，如果放置物体重量过大或载荷不均匀，则管片结构失去受力平衡，更严重的情况是可能会造成管片损坏。