有轨电车端部转向架心盘偏置最优距离研究

周业明，周思宇，王 刚，任利惠

（1.中车青岛四方机车车辆股份有限公司，山东青岛 266111；2.同济大学铁道与城市轨道交通研究院，上海 201804）

1 研究背景

现代有轨电车有多种形式，按车体结构形式划分，可分为铰接式车体和非铰接式车体[1]。Skoda 15T 有轨电车是非铰接车体有轨电车的典型代表，其车体转向架采用2 种带有心盘摇枕结构的独立车轮转向架，分别是端部转向架和Jaccobi 转向架[2]。与一般转向架不同的是，端部转向架的心盘在纵向方向不与转向架的几何中心重合，而是偏向车辆内端设置。

研究表明，转向架的心盘偏置会影响端部转向架前、后轮对的轮轴横向力分配，进而影响车辆的曲线通过安全性[3-4]。当端部转向架心盘向车辆内端偏置时，会减小前轮对的轮轴横向力、增加后轮对的轮轴横向力。

轮轴横向力对于轨道车辆而言是一项重要的安全性指标。当轮轴横向力过大，将造成轨道永久的横向变形或者一侧钢轨发生扭曲现象。为减小轮轴横向力、提高车辆的运行安全性，需要探究合理的转向架心盘偏置距离。

2 最优偏置距离

2.1 Skoda 15T 有轨电车

Skoda 15T 有轨电车通常由3 个车体和4 个独立车轮转向架组成，结构示意如图1 所示，其中2 个司机端车体的车头支撑在端部转向架上，车尾支撑在Jaccobi转向架上，中部车体的2 端分别支撑在2 个Jaccobi 转向架上。端部转向架和Jaccobi 转向架均为带有摇枕结构的独立车轮转向架。2 种转向架的不同之处在于二系悬挂。中部转向架为Jaccobi 转向架，具有2 套二系悬挂装置，每套二系悬挂包括1 对中央钢弹簧、1 个摇枕和1 对拉杆，其架构如图2a 所示。端部转向架只有1个心盘偏置的摇枕，摇枕通过二系悬挂系统与转向架构架相连，车体落在心盘的球面法兰上，其架构如图2b所示。2 个端部转向架在结构上是镜像对称的，心盘在纵向方向上均向车辆内端偏置。

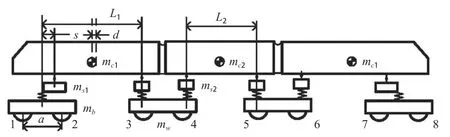
图1 Skoda 15T 有轨电车编组示意图

2.2 轮轴横向力简化计算公式

由于有轨电车通过的线路曲线半径小，且轨道通常不设置超高或设置的超高值很小，因此在通过曲线路段时会产生较大的不平衡离心加速度，因而在分析受力状态时不能忽略惯性力。本研究为推导轮轴横向力的计算公式，以车体、转向架构架、摇枕和轮对为研究对象，建立Skoda 15T 有轨电车稳态通过曲线的理论受力状态模型。Skoda 15T 有轨电车通过曲线时所受惯性力状态如图3 所示。

图3 有轨电车通过圆曲线受力分析模型

根据图3 和Skoda 15T 2 模块有轨电车的受力分析模型，得出端部车体、构架、摇枕和轮对的准静态平衡方程。

其中，车体准静态平衡方程为：

构架准静态平衡方程为：

摇枕准静态平衡方程为：

轮对准静态平衡方程为：

式（1）～式（3）中，ay表示未平衡离心加速度；Fjy1、Fjy2表示心盘与车体之间的横向力；Fssx表示二系悬挂纵向力；Fssy表示二系悬挂横向力；Fpy1、Fpy2表示一系悬挂横向力；Fey表示横向止挡的横向力；H表示轮轴横向力；分别表示车体、构架和轮对的摇头角。其他参数含义如表1 所示。

表1 车辆参数

同理可以得到中间车体的静态平衡方程。

考虑到图3 中Skoda 15T 有轨电车前后结构镜像对称，可以假设1 位、8 位轮对的轮轴横向力相同，2 位、7 位轮对，3 位、6 位轮对，4 位、5 位轮对均同理。

根据车体、摇枕、构架、轮对的横向静态平衡方程，可以推导出各个轮对的轮轴横向力公式为：

2.3 轮轴横向力因子

目前，世界上对于轮轴横向力的规范大多要求不能超过轮轴横向力极限值，该极限值与轮对轴重相关。轮轴横向力作为评定车辆在运行过程中是否会因为过大的横向力而导致钢轨扭曲、轨距扩宽或线路产生严重变形，是一项重要的安全性指标，因此保证有轨电车轮轴横向力满足标准具有现实意义。

EN 14363 : 2016《Railway applications-testing and simulation for the acceptance of running characteristics of railway vehicles-running behavior and stationary tests》对于机车、牵引单元以及客车轮轴横向力的要求[5]如式（6）所示：

式（6）中，H为轮轴横向力；P为轮对轴重；k为车辆类型系数，机车、动车、客车等取k=1.0。

对于Skoda 15T 有轨电车，由于司机端车体的重量由3 个轮对支撑，中间车体的重量由2 个轮对支撑，因此每个轮对的轴重并不相同。上述的轮轴横向力标准只能判断轮轴横向力是否超出限度。为更好的评价各轮对轮轴横向力的危险程度，定义轮轴横向力因子如式（7）所示：

所谓轮轴横向力因子，是根据轮轴横向力标准推演而来，在数学上两者意义相同。但是，轮轴横向力因子D是一个无量纲的变量，安全限度值为1。

根据以上分析可知，轮轴横向力因子具有以下特点：

（1）轮轴横向力因子与EN 14363 : 2016 对轮轴横向力极限值的规范相同；

（2）轮轴横向力因子是一个标量，不仅可以判断轮轴横向力是否超出极限值，还可以对比出整列车每个轮对轮轴横向力的相对危险程度，对于不同轴重的轮对，轮轴横向力因子更加直观；

（3）对于轴重相同或者不同的列车而言，轮轴横向力因子都只有1 个极限值，即为1。

（4）对于整个车辆，当各轴的轮轴横向力因子相等时，车辆的性能达到最优。

2.4 心盘最优偏置距离

根据公式（7）可知，轮轴横向力因子与轮对的轴重及轮轴横向力有关。当轮对处于静态载荷时，各轮对轴重为：

式（8）中，g为重力加速度。

当端部转向架的心盘处在最优偏置距离sop时，有

将式（5）、式（8）代入式（9）中，可得到下列等式：

由式（10）可知，心盘的最优偏置距离只与车辆的本身参数有关，而与车辆的运行速度、线路半径无关。将表1 中的参数代入式（10）中，求解得到本车的最优心盘偏置距离为0.13 m，比2 模块Skoda 15T 有轨电车的最优心盘偏置距离要稍小一些[3]。

3 心盘偏置对曲线通过性能的影响

3.1 动力学模型

使用Universal Mechanism 软件建立图1所示有轨电车的多体动力学模型。该模型由37 个刚体组成，其中包括3 个车体、4 个转向架、6 个摇枕、8 个轴桥和 16 个独立的旋转车轮。动力学模型和拓扑关系如图4 所示。

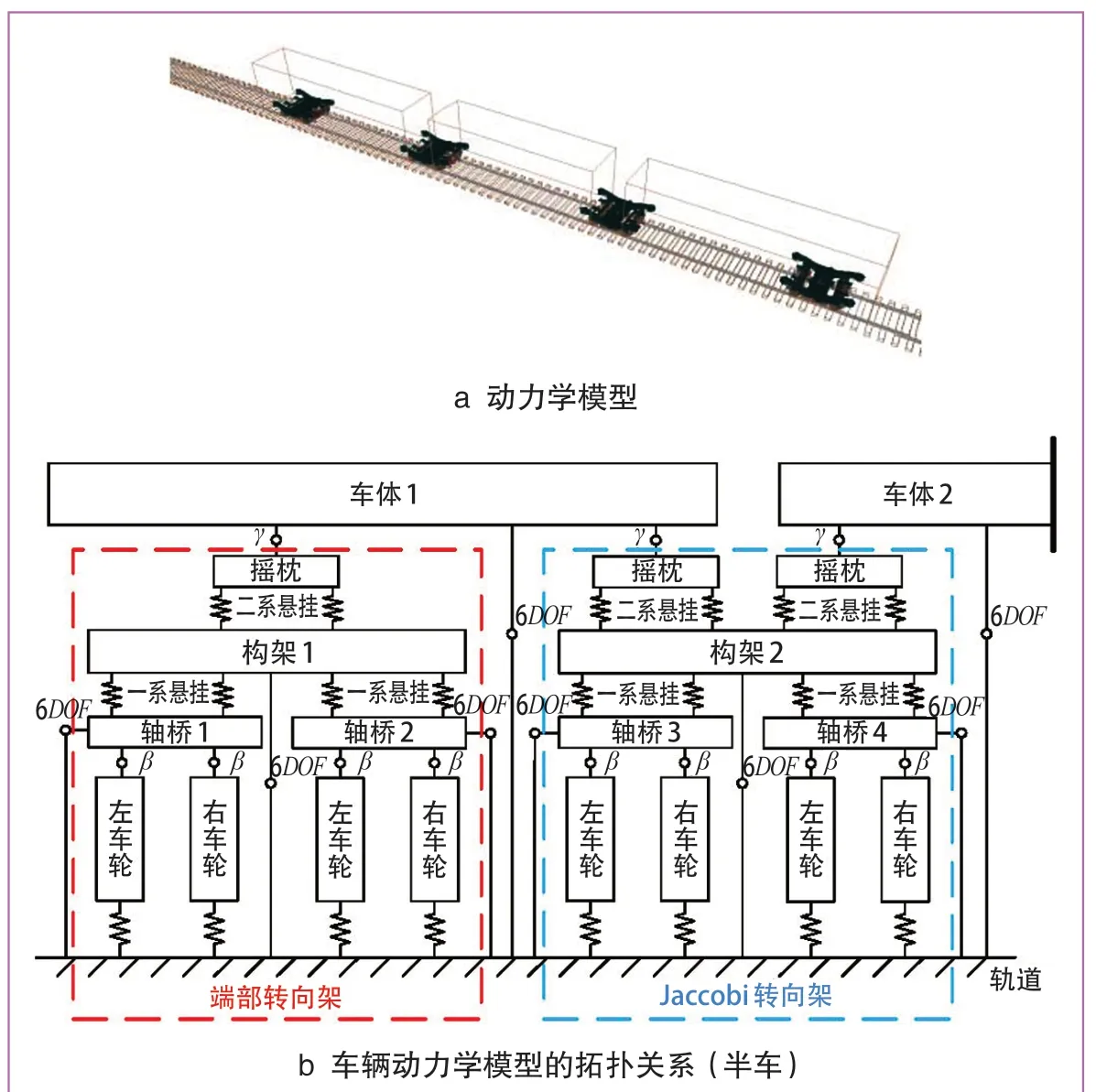
图4 车辆动力学仿真模型

3.2 仿真结果

根据建立的动力学模型，将心盘分别在负偏置（-0.2 m）、不偏置（0）、最优偏置（0.13 m）、过偏置（0.2 m，0.3 m）状态下，仿真计算有轨电车以30 km/h 速度通过半径为100 m 曲线时的动力学性能。取轮轴横向力、轮轴横向力因子和脱轨系数作为曲线通过性能的评价指标。

3.2.1 轮轴横向力简化计算公式验证

轮轴横向力的仿真值和按照式（5）的计算结果如图5 所示。图中结果表明，心盘偏置距离在-0.2～0.3 m 范围内时，3 位、6 位轮对的轮轴横向力大于其余轮对的轮轴横向力，1 位、2 位、7 位、8 位轮对的轮轴横向力随着心盘偏置距离的改变变化明显。仿真结果和公式计算结果具有较好的一致性，验证了式（5）的准确性。

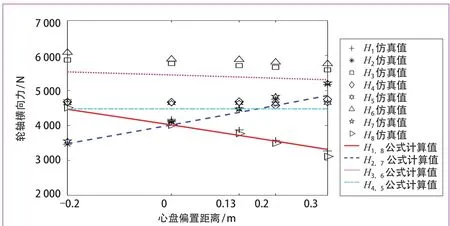
图5 轮轴横向力

3.2.2 轮轴横向力因子

每个转向架轮轴横向力因子的最大值如图6 所示。从图中可以看出，随着心盘偏距从负到正变化，第2 位、3 位转向架的轮轴横向力因子单调下降，而第1 位、4 位转向架的轮轴横向力因子先下降后快速上升，在心盘处于不偏置状态时达到最小值；心盘在负偏置和不偏置状态时，第3 位转向架的轮轴横向力因子要大于其他3 个转向架的数值，心盘在过偏置状态时，第1 位转向架和第4 位转向架的轮轴横向力因子要大于剩2 个转向架的数值，在最优偏置距离时，4 个转向架的轮轴横向力因子接近一致，整车的轮轴横向力因子达到最小值。

图6 轮轴横向力因子

3.2.3 脱轨系数

脱轨系数的最大值如图7 所示。从图中可以看出，随着心盘偏距从负到正变化，第1 位、2 位、3 位转向架的脱轨系数为单调下降，而第4 位转向架的脱轨系数单调上升；心盘在小于最优偏置距离前，2 位转向架的脱轨系数大于其他3 个转向架，而在大于最优偏置距离后，4 位转向架的脱轨系数大于其他3 个转向架；在最优偏置距离，4 个转向架的脱轨系数接近，整车的脱轨系数达到最小值，车辆具有最优的动力学性能指标。

图7 脱轨系数

4 结论

针对Skoda 15T 有轨电车端部转向架心盘偏置现象，建立Skoda1 5T 有轨电车稳态通过曲线的受力分析模型，推导出轮轴横向力与转向架心盘偏置距离的计算公式。针对目前评价轮轴横向力标准的不足，提出轮轴横向力因子概念，用于评价不同轴重条件下各个轮对的轮轴横向力安全性。基于整列车辆的轮轴横向力因子达到最小的原则，推导出满足这一原则的心盘偏置距离，称之为最优偏置距离。

经动力学仿真分析转向架心盘偏置距离对曲线性能的影响表明，当转向架心盘处于最优偏置距离时，整个车辆的轮轴横向力因子和脱轨系数达到最小值，车辆具有最优的动力学性能指标。