基于双变量自适应“当前”统计模型的场面4D轨迹跟踪预测

2024-01-30鲁其兴汤新民

系统工程与电子技术 2024年2期

鲁其兴, 汤新民, 周杨

(1. 南京航空航天大学民航学院, 江苏南京 211106;2. 中国民航大学交通科学与工程学院, 天津 300300)

0 引言

随着机场场面航空器密度的增加,管制员和飞行员负荷加重,场面运行产生潜在不安全事故的可能性增大[1-2]。尤其在航空器进场过程中,由于航空器落地时速度较大,飞行员需要根据飞机的位置、姿态和场面实际情况对飞机进行一系列复杂控制操作,导致跟踪模型易出现失配问题,使航空器发生机动现象。因此,为了规避航空器在跑道和滑行道上可能存在碰撞冲突的风险,提高航空器轨迹预测的精确性,急需利用场面监视技术对机场航空器4D轨迹进行精准跟踪预测,以实现场面目标冲突解脱的精确控制[3-4]。

广播式自动相关监视(automatic dependent surveillance-broadcast, ADS-B)技术是一种机场场面监视新技术,航空器通过ADS-B对外广播报文信息的方式,为场面ADS-B接收机提供实时准确的时间、位置、高度、航向和速度等主要参数信息,从而有效地优化场面管理,提高运行效率[5-7]。与传统雷达、红外等传感器数据相比,ADS-B数据传导方式具有独特优势。在ADS-B定位精度方面,其监视技术信息源来自机载全球卫星导航系统(global navigation satelite system,GNSS)接收机,核心是高精度卫星导航,其定位精度能达到10 m量级,远高于传统雷达,监视信息刷新率为1 Hz,是传统雷达的10～15倍,信息更准确、及时;在可靠性方面,ADS-B广播数据采用全向发射,传统雷达采用波束扫描,导致雷达信号易被遮挡,造成信号丢失,因此ADS-B更为可靠;在成本效益方面,一套传统雷达的建设成本大约为100万～400万美元,而一套ADS-B地面站建设成本在10万美元左右,且维护相对容易,成本效益最优。对红外技术而言,其无法控制目标辐射的工作频率,且受目标表面及背景辐射的干扰,对目标的分辨率较差,不能准确反映目标位置等数据信息;另外,其定位测量受时间、温度影响较大,检测结果解释比较复杂,精确度较低,在机场航空器跟踪预测中应用较少,因此ADS-B技术在机场监视领域得到了广泛应用。由于ADS-B对外广播的特点,其易受复杂场面环境和无线电杂波等干扰,因而ADS-B的观测轨迹样本时间序列是不等间隔的,并且较航空器实际运动轨迹相比易出现偏差。航空器轨迹跟踪的难点在于复杂场面非线性非高斯有色噪声状态下,运动模型、滤波算法、固定参数等难以确定,致使跟踪性能降低,甚至发散[8-10]。因此,建立合适的运动模型和自适应算法,对机动目标ADS-B轨迹数据进行跟踪预测,是解决这些问题的关键点。

ADS-B技术利用全球定位系统(global positioning system, GPS)实现空对空、地对空及地对地的数据链通信监视,其融合于当前统计模型实现航空器航迹滤波,通过估计航空器状态得到实时变化的加速度均值,相比传统算法,能够更好地实现加速度分布实时修正,进而将修正结果反馈到下一时刻的滤波增益中,实现对场面航空器的精准跟踪,在机场交通流量监视方面起到了重要作用。机场场面机动目标跟踪是航空器在运动过程中由于动力学特性发生变化,导致场面目标跟踪模型出现突变,从而对机动目标进行最优状态估计的问题[11-13]。在场面机动目标跟踪模型中,传统的恒定速度(constant velocity, CV)、恒定加速度(constant acceleration, CA)模型无法适应机场有色噪声过程,而Singer模型采用加速度为指数自相关零均值、近似均匀分布的模型[14],但由于机场场面实际情况复杂多变,加速度均匀分布的假设并不合理,其对航空器轨迹跟踪精度较差。周宏仁[15]提出“当前”统计模型自适应滤波(current statistical model adaptation filter, CS-AF)算法,但是经典CS-AF算法的机动频率和加速度极限值需要由先验知识提前假定,而固定的模型参数使滤波性能受影响较大。对此,国内外学者提出许多改进的CS-AF算法,其中文献[16]和文献[17]通过模糊推理依据量测信息及变化率推出实时选取的机动频率,通过构造隶属度函数,提出一种最大加速度模糊自适应调整的当前统计模型;文献[18]和文献[19]利用卡尔曼滤波协方差和新息向量的变化,依据机动检测设置门限,通过增加调整因子的方法,对机动频率和加速度方差进行自适应调整;文献[20]通过泰勒级数展开和忽略高阶项的方法得到模型加速度极值和均值的修正结果,引入强跟踪滤波器,增强了机动目标自适应跟踪能力。文献[21-24]利用传统交互多模型(interacting multiple model, IMM)与强跟踪及无迹卡尔曼滤波器相结合的方式,将“当前”统计(current statistical, CS)模型引入IMM框架内,通过计算后验概率,实现统计模型自适应调整。以上方法计算量比较大,且会发生时间滞后性,不利于场面监视设备对航空器进行实时跟踪。

综上,针对经典CS-AF算法固有机动频率与加速度极限值在模型跟踪中的缺点以及对不等时间间隔轨迹序列的跟踪问题,本文提出一种双变量自适应改进的CS-AF(modified CS-AF, MCS-AF)算法,即:令采样时间间隔T为前后两时刻之差,并利用加速度一阶时间相关过程模型,依据一阶导数定义,对加速度进行分析,同时利用运动学理论模型和修正的位置估计滤波残差,实时在线修正目标状态。通过在ADS-B真实数据中进行仿真验证,改进的MCS-AF算法在模型跟踪精度和轨迹拟合方面均优于CS-AF算法。

1 坐标转换与系统模型构建

1.1 坐标转换

坐标转换是机场场面目标跟踪预测的基础,在同一平台内,不同坐标系传感器量测值必须统一到同一坐标下[25]。坐标转换流程如图1所示。

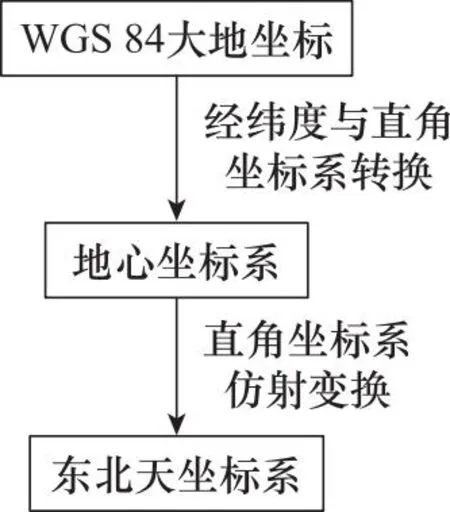
图1 坐标转换流程图Fig.1 Flowchart of coordinate conversion

本文建立的坐标系均符合右手系规则,以地球中心oi为圆心,建立地心坐标系(xi,yi,zi),以机场基准点og为原点,建立东北天坐标系(xg,yg,zg),如图2所示。ADS-B报文中目标位置采用WGS-84大地坐标系(B,L,H),其中:B为纬度,L为精度,H为飞行高度[26]。

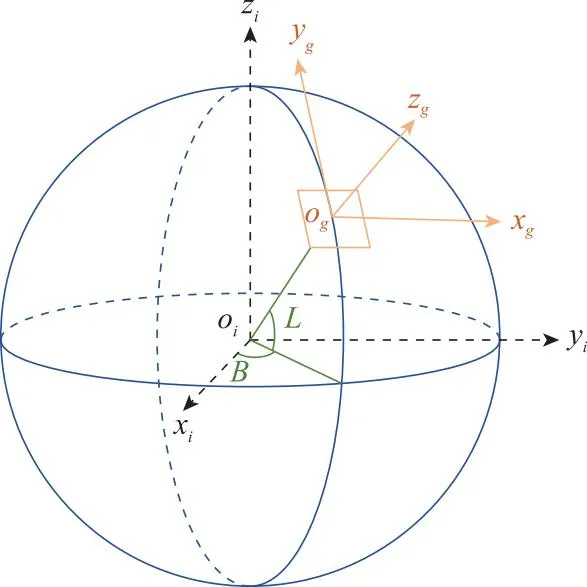
图2 地心坐标系和东北天坐标系Fig.2 Geocentric coordinate system and northeast celestial coordinate system

为了便于分析场面航空器运动状态,需将ADS-B经纬度信息转换为东北天坐标系下的平面直角坐标。首先将经纬度转换为地心坐标系下的绝对坐标,即

(1)

式中:a为地球长半轴 (6 378 137 m);b为地球短半轴 (6 356 752 m);e为地球第一偏心率。

通过式(1),计算出机场基准点绝对坐标为(xi0,yi0,zi0),ADS-B轨迹数据点的绝对坐标为(xi1,yi1,zi1)。然后,计算出轨迹点相对于基准点的相对坐标(X1,Y1,Z1),最后,依据仿射变换原理,通过旋转矩阵RT,得到航空器在东北天坐标系下的直角坐标。计算过程如下:

(2)

RT为旋转矩阵:

(3)

经过坐标转换,可以实现ADS-B任一轨迹数据点相对于机场基准点的直角坐标,为后面的实验分析提供了数据支持。

1.2 系统模型构建

当目标以某一加速度发生机动时,下一时刻的加速度取值只能在“当前”加速度的领域内,加速度均值为非零值,加速度统计特性满足修正的瑞利分布[27]。

根据上述条件,加速度模型构建为

(4)

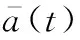
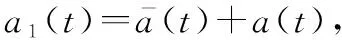
(5)

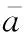
为了方便分析,利用白化滤波器将有色噪声进行白化处理,并对连续系统进行离散化,得到CS模型二维状态下离散系统的状态方程和观测方程[28],即

(6)

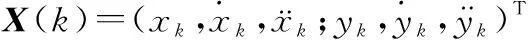
其中,

W(k)的方差为

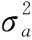
通过观察CS模型参数可知,在系统运行过程中,对机动频率的取值需要通过实测或根据先验知识获得,而加速度方差可以利用加速度极限值和修正瑞利分布的概率密度函数通过消去中间变量计算得到[30],其表达式为

(7)

1.3 CS-AF场面跟踪现存不足

(1) 固定的机动频率与加速度极限值易造成CS-AF算法在突发机动状态下状态估计残差变大,跟踪性能降低,且在ADS-B真实数据中跟踪性能较差,速度和加速度状态估计误差偏大,易出现滤波发散的情况。

(2) 基于机场场面ADS-B数据是以无线电对外广播的形式进行数据传输,因此接收机收到的场面真实数据基本为不等间隔的时间序列,然而绝大部分文献研究主要是以仿真数据为主,且基本上都是等时间间隔,缺乏真实性,无法反映场面航空器轨迹跟踪的实际情况。

(3) 机动频率与加速度极限值在模型跟踪效果上具有较强依赖性,依据式(7)可知,若加速度极限值设置较大,当目标不机动或弱机动时,目标加速度稳态估计值与极限值相差较大,易发生较大过程噪声;设置较小时,目标的实际加速度超过其预设值,模型跟踪性能将显著下降。机动频率较大时,加速度相关性变弱,对匀速或弱机动目标跟踪精度降低,而机动频率较小时,对连续强机动目标的跟踪效果将明显降低。

针对上述问题,本文提出一种双变量自适应的MCS-AF算法,实现了机动频率和加速度方差在线实时调整与自适应估计,对场面航空器进行精准跟踪与态势感知预测具有重要作用。

2 双变量自适应MCS-AF算法

2.1 机动频率实时在线调整

依据加速度一阶时间相关过程模型,利用导数定义,对加速度进行分析,具体实现过程如下:

对式(5)两端同时求期望,得:

(8)

式中:ω(t)为零均值,因此E(ω(t))=0。当时间间隔T较小时,依据导数定义可知:

(9)

对式(9)进行离散化,得:

(10)

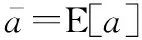
(11)

由于机动频率α>0,将式(11)代入式(10),得:

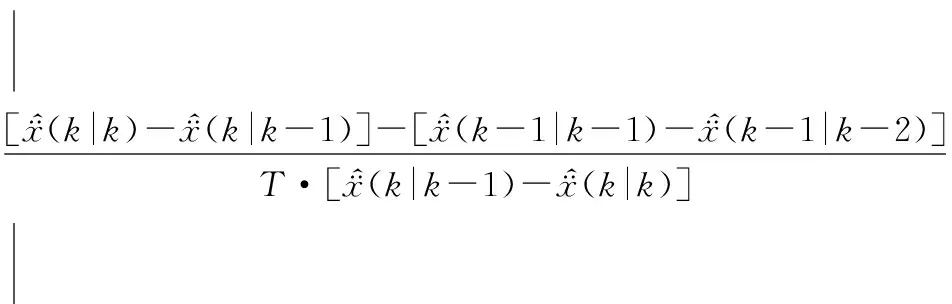
(12)

通过分析,利用当前加速度状态估计值与状态预测值之间的差值进行机动频率求解,使其实现实时在线自适应更新。当航空器发生机动时,加速度的相关性降低,加速度前后两时刻的估计值变大,α相应变大,与理论结果相一致。通过实时调整α,确保了航空器运动模型与运动模式实时统一,避免了固定α带来的跟踪偏差,提高了跟踪精度。

2.2 机动目标加速度方差实时在线调整

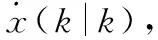
航空器在k时刻的位置状态预测估计值为

(13)

航空器运动轨迹在经过残差修正后,k+1时刻估计值为

(14)

式中:Δv(k)=|Δa(k)|T,则k+1时刻航空器加速度变化率为

(15)

由于Δa(k)为对称矩阵且为加速度变化值,则机动加速度方差为

(16)

联立式(15)和式(16),得到机动目标改进的加速度方差自适应算法为

(17)

通过分析可知,当航空器发生机动时,加速度变化量增大,相对于其数学期望值分散程度加大,加速度协方差变大,航空器状态估计值偏离其预测值的程度加大,运动方式符合理论结果,并且实现了加速度方差的自适应调整,较好地反映了机动与非机动的真实情况,避免了固定机动频率的影响,使跟踪精度得到进一步提高。

2.3 机动目标卡尔曼滤波自适应调整

将改进的机动频率和加速度方差融入卡尔曼滤波算法,既实现了机动频率与加速度方差实时自适应调整,同时也兼顾了机场场面航空器在复杂运动、机动状态多变的环境下平稳滑行。融合后的MCS-AF跟踪算法步骤如下[32]:

(1) 目标状态预测:

(18)

在目标状态一步预测过程中,一步预测状态转移矩阵为

(19)

(2) 状态变量协方差预测:

P(k+1|k)=A(k)P(k|k)AT(k)+Q(k)

(20)

(3) 滤波增益:

K(k)=P(k+1|k)HT(k)· [H(k)P(k+1|k)HT(k)+R(k)]-1

(21)

(4) 状态更新:

(22)

(5) 协方差更新:

P(k+1|k+1)=[I-K(k)H(k)]P(k+1|k)

(23)

(6) 机动频率α自适应算法:

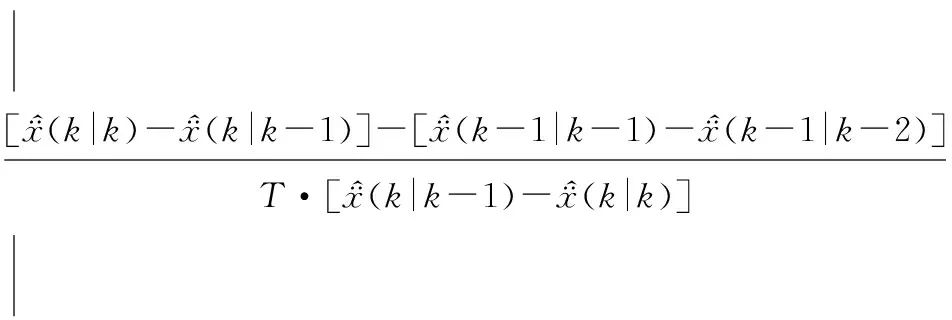
(24)

(25)

本文所提算法实现了参数辨识的自适应滤波跟踪控制,形成了“估计-模型-参数”的闭环结构,实现了机动频率和加速度方差自适应调整,理论上能够提高模型的适应能力和目标跟踪精度,更有利于实际情况中场面航空器机动目标的跟踪。下面结合场面ADS-B轨迹数据对所述模型跟踪精度进行分析验证。

3 实验结果分析

通过ADS-B接收机采集机场场面航空器从跑道到滑行道的轨迹数据,本文采用航空器的ADS-B数据,并对数据分别进行数据解码、坐标转换、数据清洗、冗余点与异常点的清除等。然后,对CS模型和改进CS模型分别进行滤波跟踪与预测,验证MCS-AF模型算法在真实的ADS-B数据中,其场面轨迹跟踪滤波的有效性,同时比较MCS-AF模型算法与CS-AF模型算法在位置、速度及加速度滤波跟踪方面的精度差异。

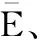
(1) 均方根误差:

(26)

(2) 误差均值:

(27)

(3) 误差标准差:

(28)

式中:Xi为第i个样本点滤波值;xi为第i个样本点真实值;N为样本点总数。

根据采集的ADS-B数据可知,以机场基准点为坐标原点,航空器初始位置(x,y)=(-2 634.27,-3 993.84) m,初始速度(vx,vy)=(36.11,55.61) m/s,航空器运动过程历时约376 s,初始机动频率α预设为0.05,测量矩阵为[100]。采样间隔T为前后相邻两时刻之差,即

T=ti-ti-1

(29)

式中:ti为当前时刻;ti-1为前一时刻。

通过仿真,得到航空器真实运动轨迹、CS-AF跟踪轨迹及MCS-AF跟踪轨迹曲线图如图3所示。从图3可以看出,航空器整体运动轨迹光滑连续且无异常点,CS-AF和MCS-AF两种算法在整体轨迹跟踪过程中效果均较好。

图3 CS-AF、MCS-AF跟踪轨迹与航空器真实轨迹对比图Fig.3 Comparison diagram between CS-AF and MCS-AF’s track trajectories and real aircraft trajectory

接下来比较航空器真实运动轨迹、MCS-AF算法跟踪轨迹和CS-AF算法跟踪轨迹在X方向和Y方向上轨迹跟踪效果,对比结果如图4和图5所示。从图中可看出,在X方向和Y方向上,两种模型算法在整体轨迹跟踪中基本与航空器真实轨迹相符。在局部放大图中,MCS-AF算法的跟踪效果略优于CS-AF算法。

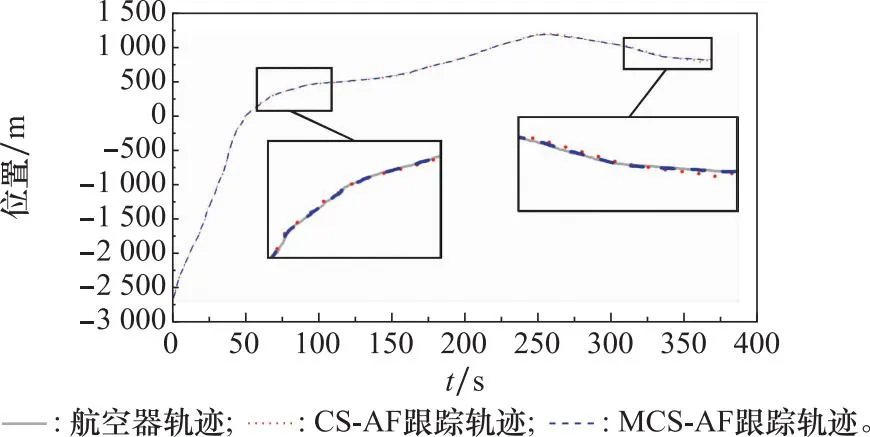
图4 X方向轨迹跟踪效果对比曲线图Fig.4 Comparison curve of trajectory track results in X direction

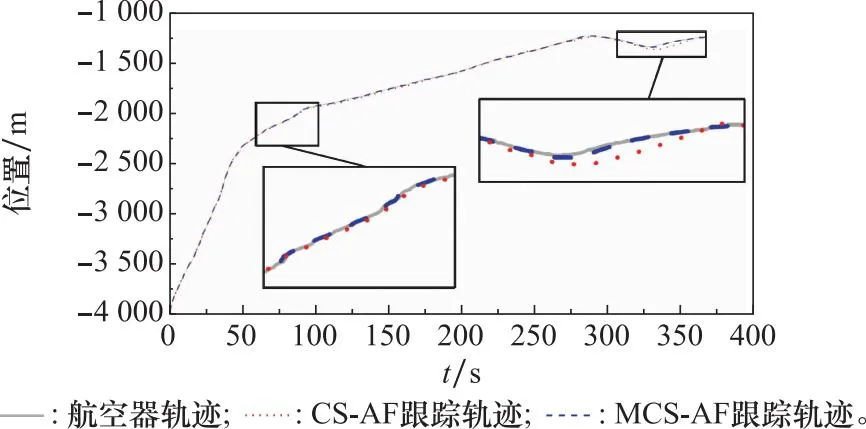
图5 Y方向轨迹跟踪效果对比曲线图Fig.5 Comparison curve of trajectory track results in Y direction

对单维度下的X值和Y值进行矢量合成,依据估计值与量测值的欧氏距离度量直角坐标系下双维度和单维度的位置、速度、加速度的跟踪误差。比较MCS-AF模型算法和CS-AF模型算法在直角坐标系下双维度和单维度的位置跟踪误差,结果如图6所示。

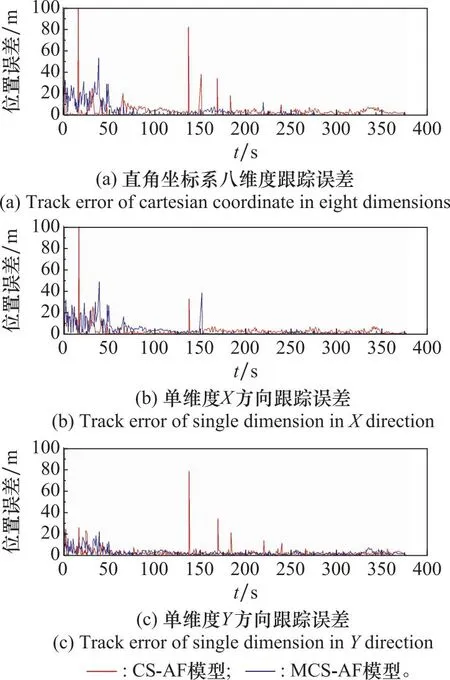
图6 直角坐标系位置跟踪误差对比曲线图Fig.6 Comparison curve of position tracking errors in cartesian coordinate

通过对图6进行分析可知:

(1) 在位置跟踪过程中,由于航空器进场时速度较大,在飞行员减速过程中,加速度变化率会出现近似跳变且快速变化的特征,因此在前期的强机动阶段,位置滤波误差较大,之后随着时间的推移,滤波误差逐渐降低,估计轨迹逐渐向真实轨迹逼近。

(2) 在速度近似平稳直线阶段,滤波误差较低且跟踪平稳,但在某几个短期时段CS-AF模型算法出现高值现象。在转弯阶段,滤波误差出现短时较小峰值现象,通过转弯后,滤波误差逐渐降低,恢复平稳。

(3) 从双维度和单维度位置跟踪误差曲线图可以看出,MCS-AF算法在滤波跟踪误差上明显低于CS-AF算法。与CS-AF算法相比,连续机动部分性能得到优化,强机动阶段和平稳阶段出现的最高峰值误差得到了明显降低,两种算法在位置机动目标跟踪上均表现出了良好的效果。

接下来比较MCS-AF算法和CS-AF算法在直角坐标系下双维度和单维度速度的加速度跟踪误差对比,如图7和图8所示。

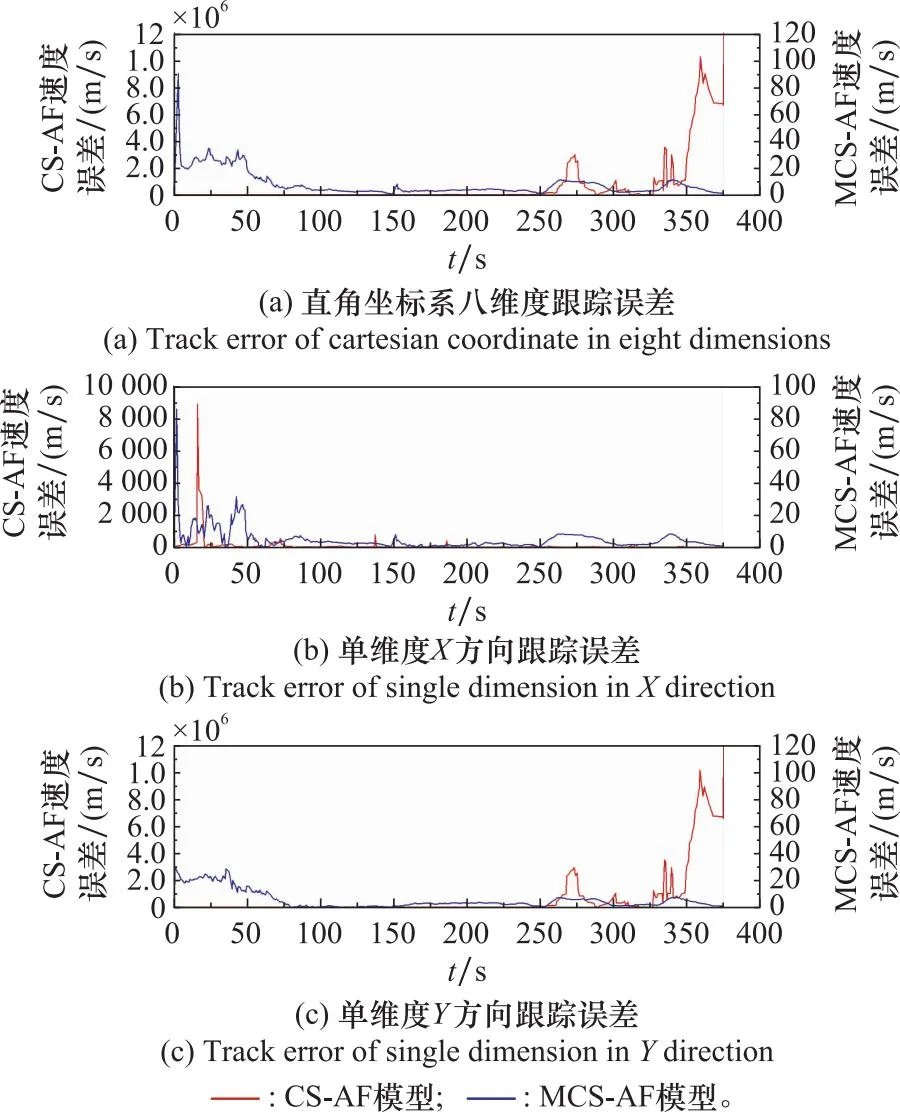
图7 直角坐标系速度跟踪误差对比曲线图Fig.7 Comparison curve of speed tracking errors in cartesian coordinate

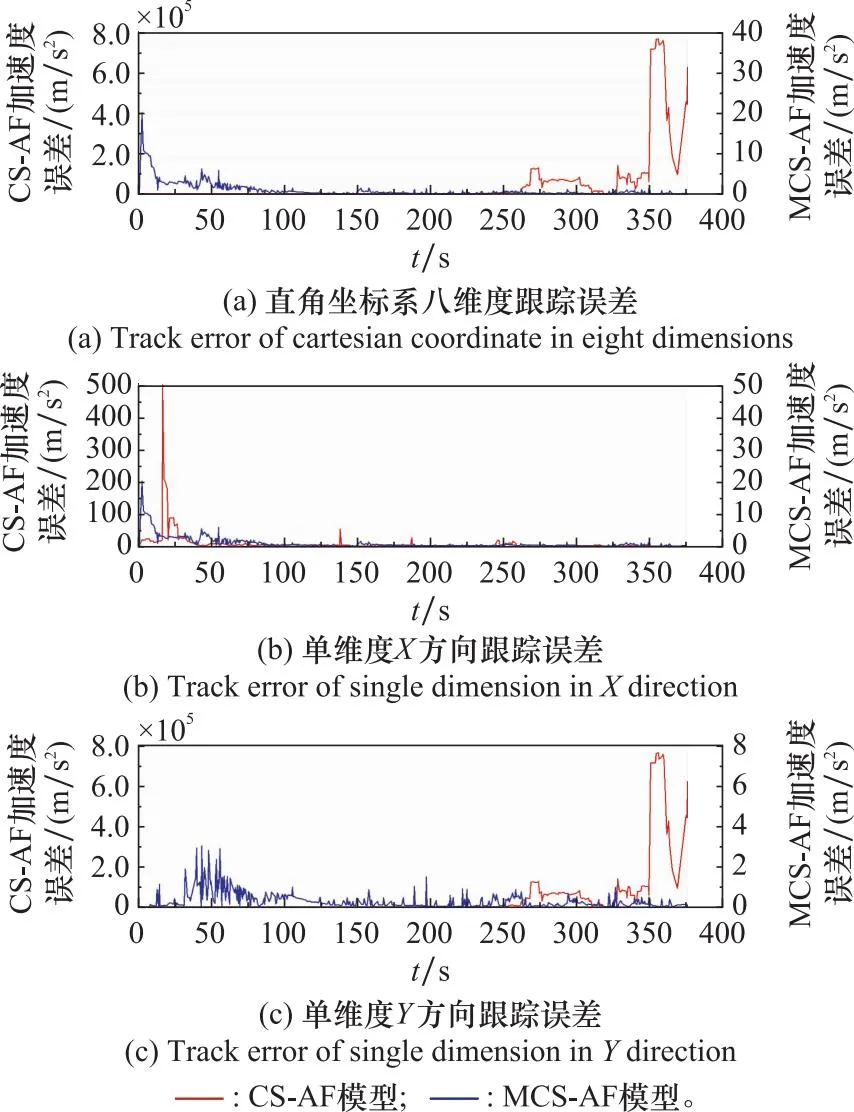
图8 直角坐标系加速度跟踪误差对比曲线图Fig.8 Comparison curve of acceleration track error in cartesian coordinate

通过对图7、图8进行分析可知:

(1) 在速度和加速度跟踪过程中,CS-AF算法在单维度X方向上强机动阶段和平稳短期时段出现了非常高的误差值,随后误差曲线收敛,但收敛效果很差;在双维度和Y方向上,速度和加速度跟踪误差曲线均出现了发散现象。

(2) 在双维度和Y方向上,MCS-AF算法的速度和加速度跟踪误差较CS-AF算法得到了有效收敛,收敛速度快且稳定。

(3) 在速度和加速度跟踪过程中,MCS-AF算法在双维度和单维度上,强机动阶段跟踪误差较大,进入滑行平稳阶段,跟踪误差较低,转弯阶段跟踪误差出现短时的增长,通过转弯后,恢复平稳;速度和加速度整体跟踪误差较低,模型算法得到了优化,跟踪精度得到了提高。

接下来详细比较了MCS-AF算法和CS-AF算法在双维度和单维度上各项评判指标在位置、速度和加速度三变量的数值对比,对比结果如表1～表3所示。

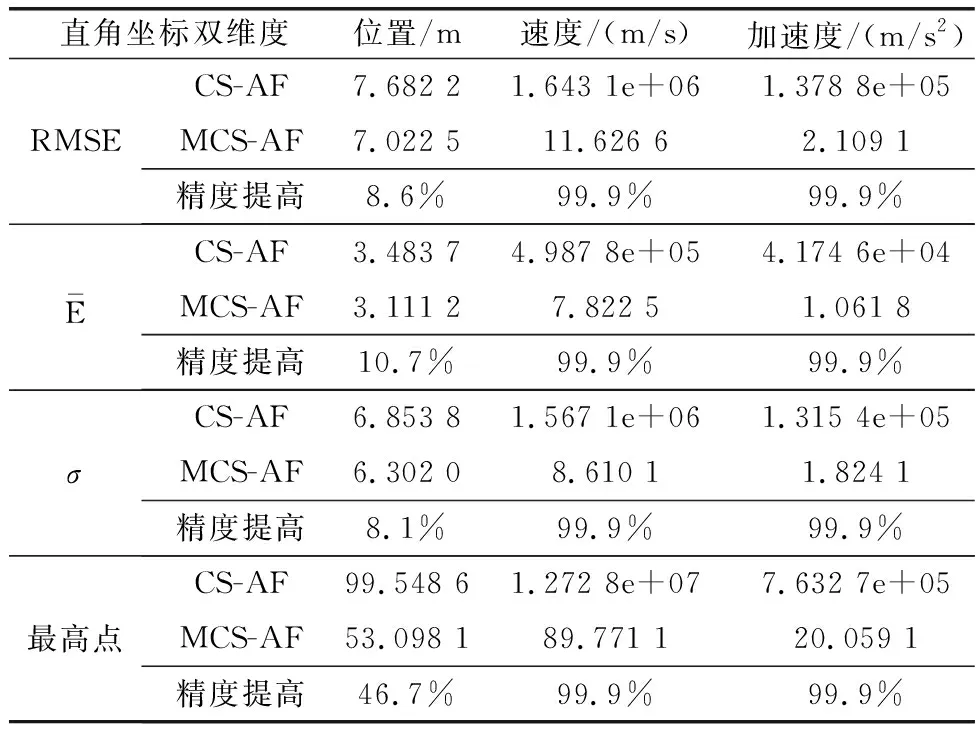
表1 双维度上位置、速度和加速度各项评判指标对比

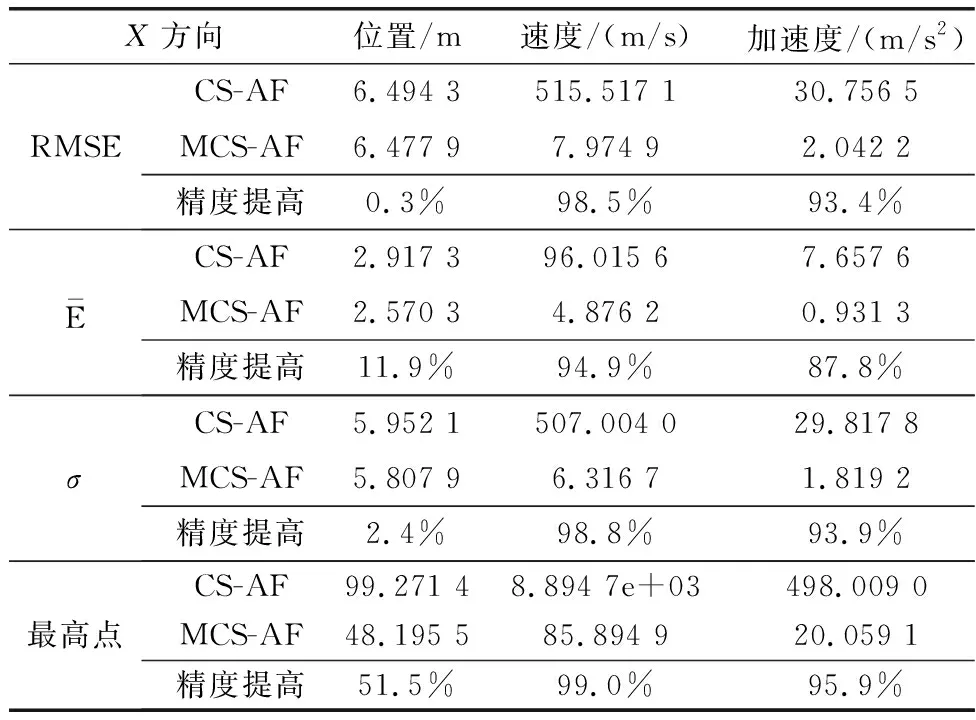
表2 X方向上位置、速度和加速度各项评判指标对比

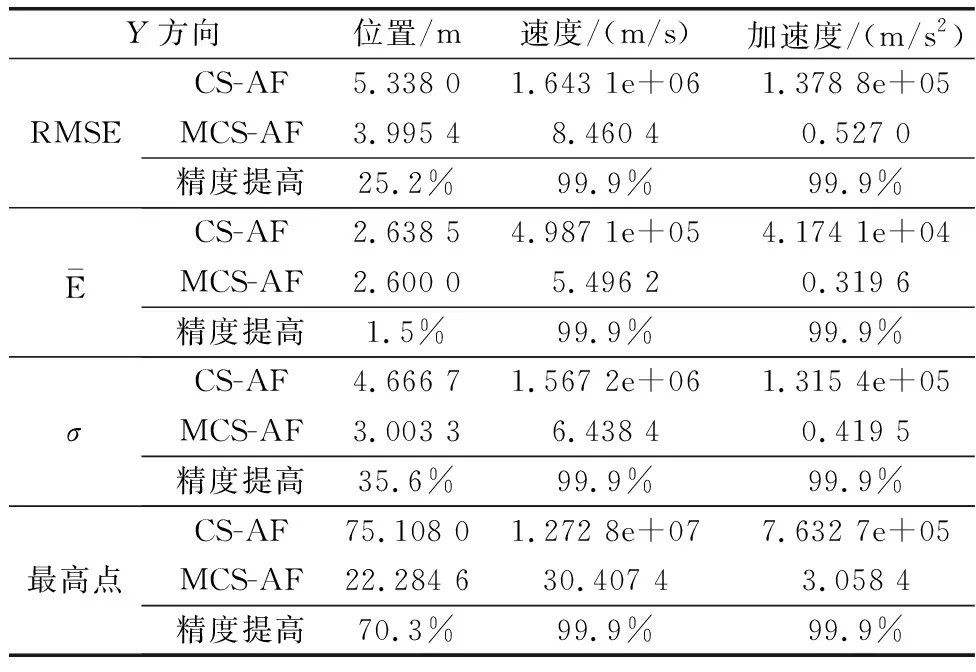
表3 Y方向上位置、速度和加速度各项评判指标对比

通过分析表1～表3可知:

(1) 航空器在双维度和单维度(X、Y方向)轨迹跟踪过程中,从其RMSE、误差均值、误差标准差、最高峰值误差4项评判指标在位置、速度和加速度三变量的数值可以看出, MCS-AF算法各项指标数据均低于CS-AF算法,其各项精度都得到了明显提高。

(2) 在轨迹跟踪过程中, MCS-AF算法的4项统计指标在位置误差跟踪过程中,双维度上的误差精度分别提高了8.6%、10.7%、8.1%、46.7%;X方向上的误差精度分别提高了0.3%、11.9%、2.4%、51.5%;Y方向上的误差精度分别提高了25.2%、1.5%、35.6%、70.3%;且在双维度和单维度Y方向上的速度和加速度跟踪误差得到了有效收敛。

(3) 根据表中各项数据可知,MCS-AF算法在一定程度上缓解了CS-AF算法对于预设机动频率和加速度极限值参数的依赖,从而优化了CS模型自适应滤波跟踪算法的性能。