卡尔曼滤波器异常自检及其在SINS初始对准中的应用
2024-01-30郭士荦王春雨
郭士荦, 王春雨, 李 洋, 田 鹏
(1. 国防科技大学信息通信学院, 湖北 武汉 430019; 2. 空军航空大学航空作战勤务学院,吉林 长春 130022; 3. 中国人民解放军93152部队, 吉林 通化 135300)
0 引 言
捷联式惯性导航系统(strapdown inertial navigation system, SINS)自主性强、隐蔽性高,是非常重要的自主式导航设备,尤其在军用领域发挥着无可替代的作用,其导航过程就是要对惯性测量单元(inertial measurement units, IMU)的输出进行积分推算[1-3],因此在进入正常导航状态之前需要给定初始值,即对其进行初始对准[4-7]。初始对准是保证SINS正常工作的关键环节,任何初始对准误差都会进入积分推算而造成系统误差。此外,IMU器件的测量误差也会在积分过程中产生累积,影响SINS的长航时导航定位精度。因此,高精度初始对准和组合导航技术成为了惯性导航技术领域的两个重要研究方向[8-11],其共性问题是对SINS误差的实时估计,而卡尔曼滤波(Kalman filter, KF)是解决该问题最常用的工具之一[12-15]。
KF通过外部观测量估计出所需信号,具有实时性好、速度快、精度高等优点,其使用的前提条件是系统的状态方程与观测方程已知,其中前者描述的是系统的激励与响应之间的函数关系;后者描述的是观测量与待估计状态量之间的函数关系。在基于KF的SINS初始对准或误差校正问题中,基本思想都是进行姿态、速度、位置等参数的误差估计,并利用估计结果对SINS的输出值进行补偿,在这一过程中通常需要根据SINS误差方程建立滤波模型。针对大失准角条件下SINS误差方程的非线性特征,学者研究了扩展KF(extended KF, EKF)[16]、无迹KF(unscented KF, UKF)[17-18]及容积KF(cubature KF, CKF)[19]等非线性滤波方法在该问题上的应用。文献[20]利用改进的EKF和UKF方法进行初始对准,证明二者精度基本相当。文献[21]基于SINS大失准角对准问题对UKF与CKF方法进行了对比分析,阐述了其各自的应用特点。
只有在准确建模且系统噪声和观测噪声满足高斯分布时,KF结果才是一致无偏估计。然而实际的一次滤波过程只会是随机过程总体中的一个样本,预设的噪声参数会不可避免地存在偏差,而这种偏差会导致滤波精度下降甚至出现发散,针对该问题的滤波优化方法也成为了学者们的研究热点。目前主要的优化策略有两种,一是基于一定准则建立的自适应滤波算法,在滤波过程中实时地对系统噪声方差阵或观测噪声方差阵进行修正[22-24];另一种是在滤波异常时,通过“膨胀”一步预测均方差阵,增加当前观测信息的作用权重,实现所谓强跟踪滤波或渐消滤波[25-28]。文献[29]指出,在滤波进程中同时对系统噪声和观测噪声参数进行自适应估计的难度很大,且引入优化策略可能对滤波稳定性和可观性存在不利影响。因此,需要采用一定的判断方法决定优化策略的引入时机,主要思想是利用滤波新息序列的理论统计特性判断实际状态的偏差情况,具体可分为协方差匹配法和卡方检验法。本文对上述两种滤波异常检验方法进行了理论分析,结合SINS初始对准实验,分别利用传统KF、UKF以及CKF对两种判据进行了对比测试,探讨了检验判据的实际效果,并给出了应用建议。
1 KF基本方程
1.1 线性KF
KF在实现形式上是一套由数字计算机执行的快速递推算法,在每一个周期内都包含状态预测和量测更新两个步骤,前者代表了历史经验信息,后者代表了即时的参考信息。这两个步骤在状态估计中的权重由滤波增益来调节。
假设一个线性离散系统,其状态方程及观测方程如下:
(1)
式中:xk∈Rn为状态向量;zk∈Rn为观测向量;Φk/k-1∈Rn×n为状态转移矩阵;Γk-1为系统噪声阵;Hk∈Rm×n为观测阵;wk与vk分别代表系统噪声序列与观测噪声序列,且满足
(2)
式中:Qk与Rk分别为系统噪声方差阵和观测噪声方差阵;δkj为Kronecker-δ函数。KF递推方程如下:
(3)
(4)
(5)
(6)
Pk=(I-KkHk)Pk/k-1
(7)
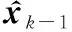
1.2 UKF
UKF对非线性函数进行概率拟合,其基本工具是无迹变换(unscented transform, UT)变换。假设一个非线性系统,其状态方程与观测方程为
(8)
式中:f(·)为状态函数;h(·)为观测函数。UKF递推过程如下。
(1) 初始化
(9)
(2) 状态预测
(10)
(3) 量测更新
(11)
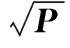
1.3 CKF
假设如式(8)的非线性系统,CKF基本方程如下。
(1) 状态预测
(12)
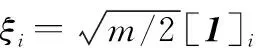
第三步通过状态方程传递容积点,第四步对k时刻的状态进行预测,最后得到预测均方差阵。
(2) 量测更新
(13)
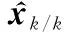
2 滤波检验判据
定义KF的新息序列为
εk=zk-Hkxk/k-1
(14)
理论情况下滤波器满足正交性原理[19]:
(15)
其物理意义为,滤波误差的方差达到最小,由于观测量中的有效信息已经被完全提取,不同时刻的新息矢量相互正交,此时新息序列协方差的理论值为
(16)
由于噪声参数建模不准或异常噪声干扰等情况导致KF过程出现异常甚至发散,此时滤波器失去最优估计性能,无法完全提取观测量中的有效信息,进而新息序列协方差会偏离其理论值,基于此可以构建第一种基于协方差匹配的异常判据(简称为判据1):
(17)
式中:λ为调节系数,用来决定异常判据的严格程度,表示实际滤波误差已经超出理论值的λ倍。当λ=1时,为最严格判断条件;tr(·)表示求迹运算。此外,还有一种基于卡方检验的异常判据(简称判据2):已知在理论情况下新息序列的统计特性符合均值为0的高斯分布,即
(18)
由此可以构造异常检测函数γk:
(19)
则γk满足χ2(卡方)分布[30-31],其自由度为量测的维度。可以利用χ2分布上分位点的性质来设计假设检验判据,例如当量测维度为3时,通过查表选取上分位点ζ=11.345,则有
P{χ2(3)>ζ}=1%
(20)
也就是说在理论情况下,γk大于ζ的概率只有1%。根据假设检验原理,在一个滤波周期中如果出现了γk>ζ,则在99%的置信度下可以认为该次滤波异常。下面通过一个简单系统的KF仿真试验说明两种判据的有效性。假设一个四维线性系统,其状态及观测方程为
(21)
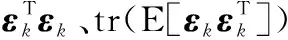
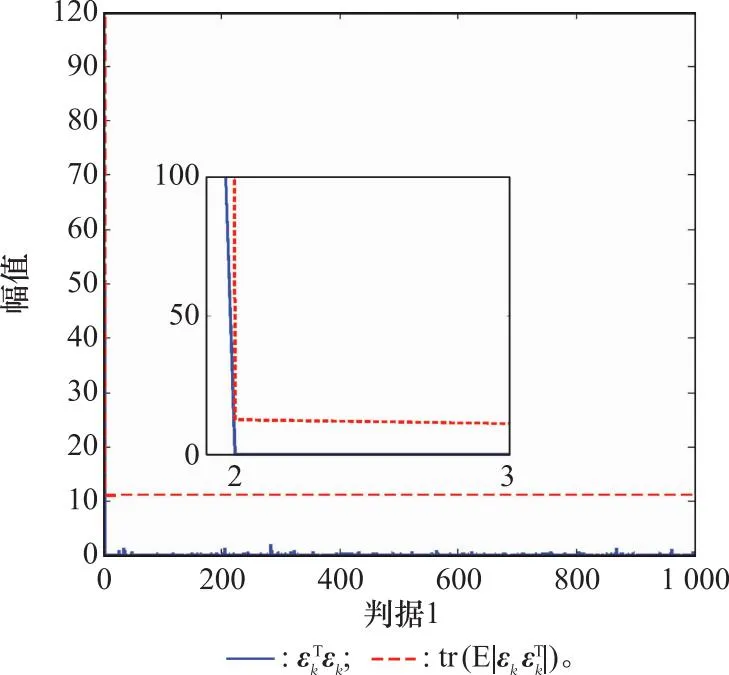
图与的对比Fig.1 Comparison between and
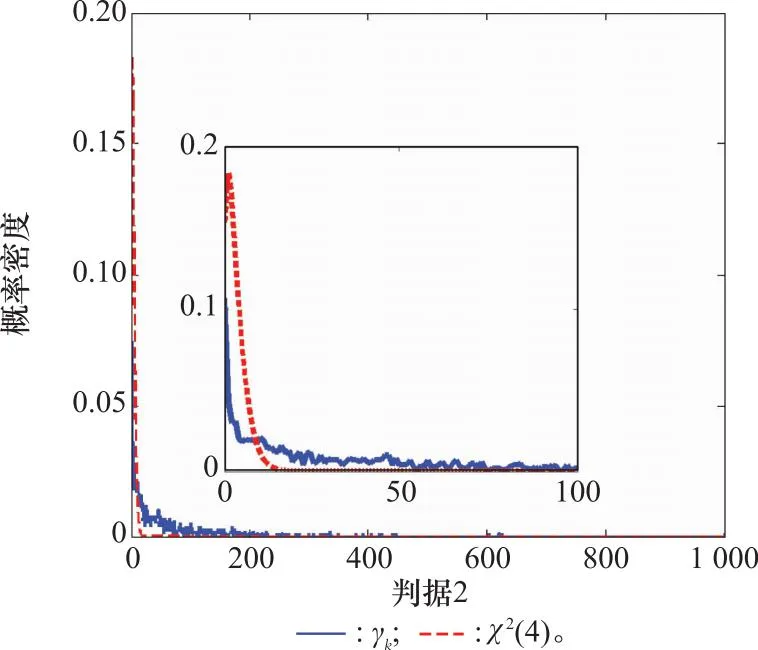
图2 γk概率分布与χ2(4)的对比Fig.2 Comparison between probability distribution of γkand χ2(4)
3 SINS误差模型
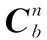
相关推导可见文献[4],此处直接给出SINS的速度与姿态误差方程:
(22)
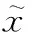
(23)
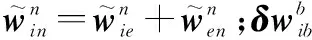
(24)
式中:
矩阵A的计算方法为
(25)
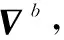
(26)
4 试验验证
基于SINS的初始对准问题,分别利用常规KF、UKF和CKF验证两种判据。
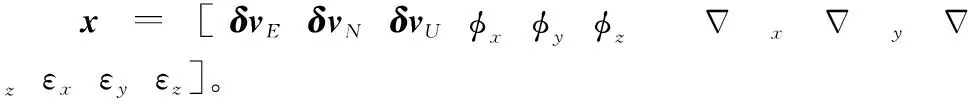
静态条件下以SINS的速度输出作为速度误差观测量,观测矩阵为Hk=[I3×303×9],其他初始条件设置为
以姿态对准误差为例,在正常滤波条件下3种滤波器均可快速收敛,得到角分级的对准精度。为了模拟异常噪声干扰情况,针对系统噪声和观测噪声的连续异常和突变异常两种状态,共设计以下3组试验。
试验 1系统噪声连续异常,400~550 s时惯性测量元件白噪声方差扩大100倍;
试验 2观测噪声连续异常,400~550 s在速度观测值中加入1 m/s的常值偏差及标准差为1 m/s的白噪声;
试验 3观测噪声突发异常,每隔200 s在速度观测值中加入5 m/s的常值偏差。
为了验证直观展现判据的检测能力,设计两个判断因子θ1和θ2,满足
即检测滤波正常时判断因子为0,反之为1。设定调节因子λ=1,同时考虑三维观测,设定ζ=11.345,即正常情况下大于ζ的概率只有1%。试验1中,航向对准误差以δφz表示,其与判断因子的取值情况如图3~图5所示。
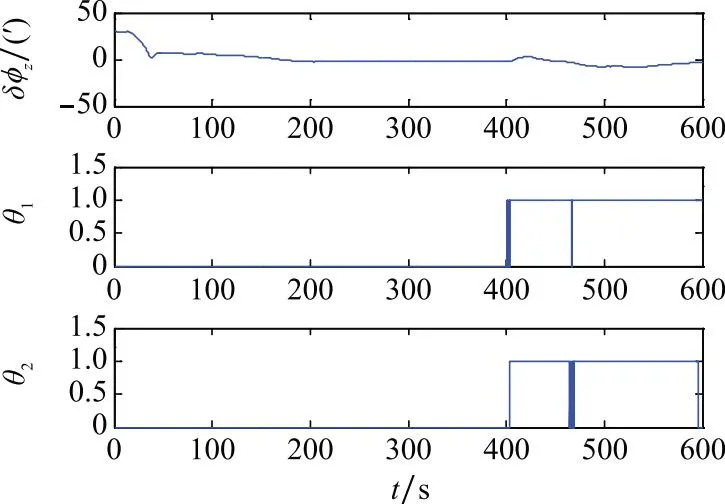
图3 试验1(KF)Fig.3 Test 1 of KF
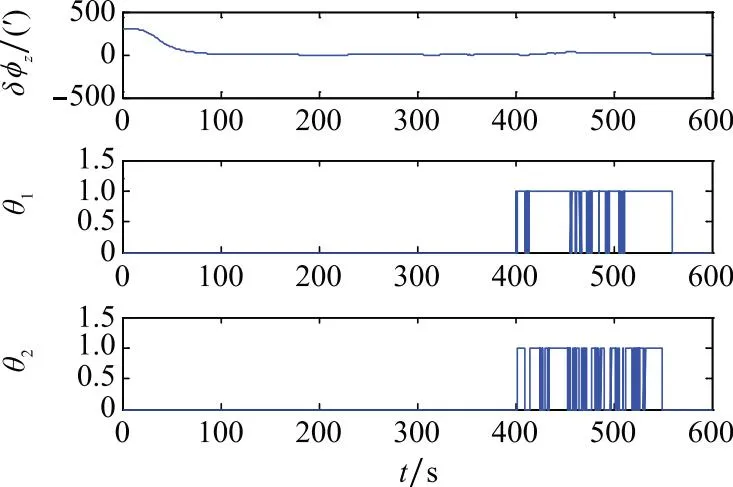
图4 试验1(UKF)Fig.4 Test 1 of UKF
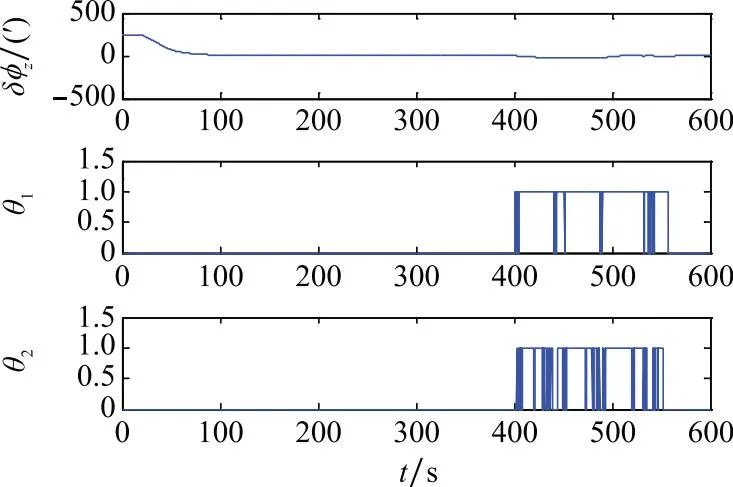
图5 试验1(CKF)Fig.5 Test 1 of CKF
图3~图5为第一组试验中两种判据的检验效果。在400~550 s内,判据1和判据2的异常检出率如表1所示。
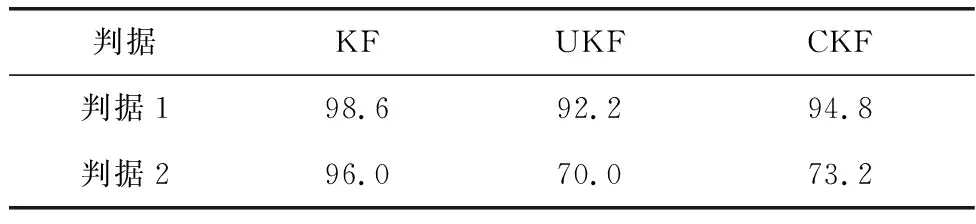
表1 试验1的异常检出率
显然两种判据对本文设置的连续系统噪声异常均具有一定检出能力,但判据1的检验严格程度明显高于判据2。试验2中3种滤波器对航向通道的估计误差δφz与判断因子的取值情况如图6~图8所示。
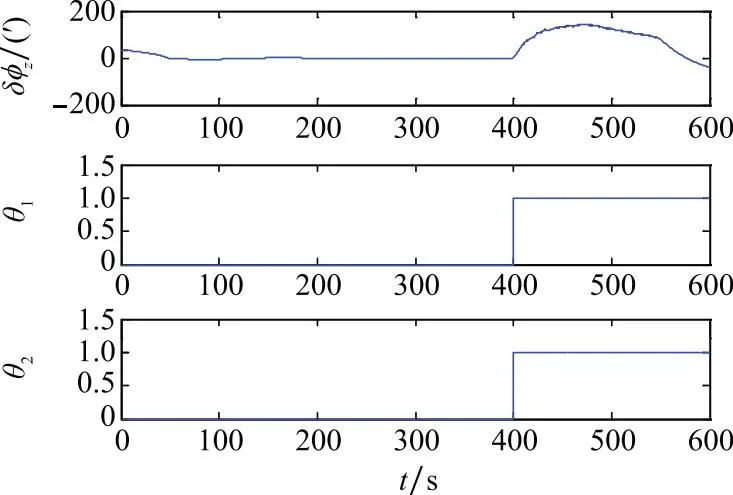
图6 试验2(KF)Fig.6 Test 2 of KF
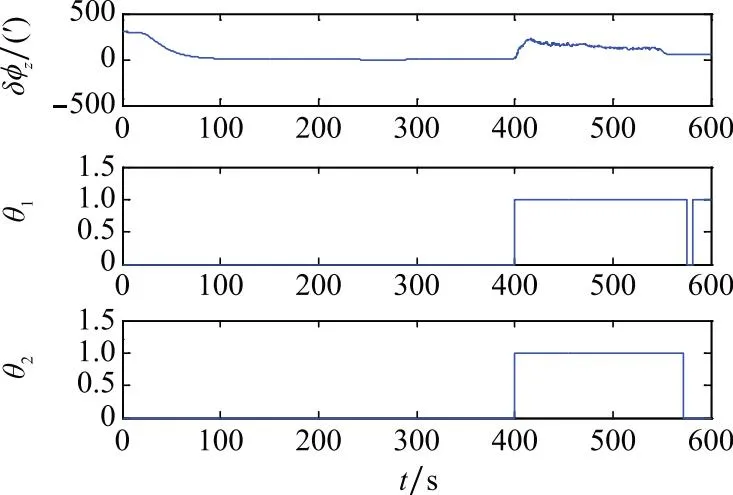
图7 试验2(UKF)Fig.7 Test 2 of UKF
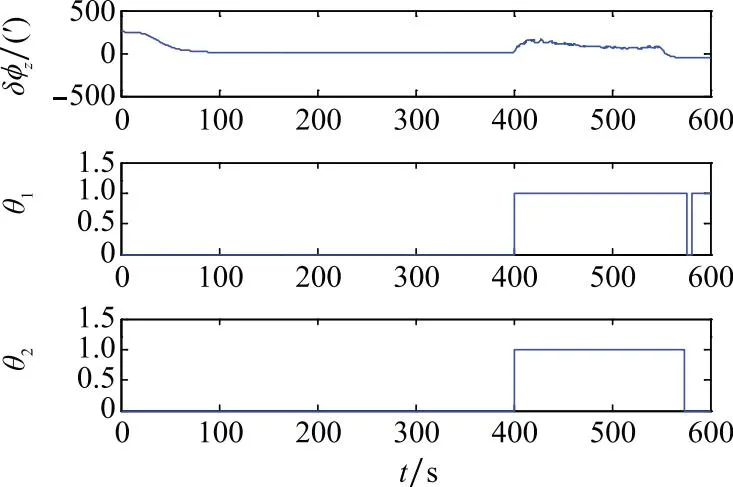
图8 试验2(CKF)Fig.8 Test 2 of CKF
图6~图8为第二组试验中两种判据的检验效果。在400~550 s内,两种判据对本文设置的连续观测噪声异常的检出率均为100%。试验3中3种滤波器对航向通道的估计误差δφz与判断因子的取值情况如图9~图11所示。
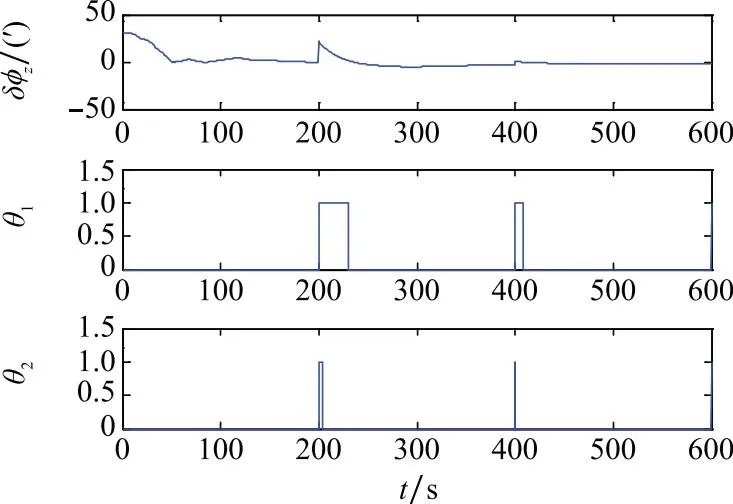
图9 试验3(KF)Fig.9 Test 3 of KF
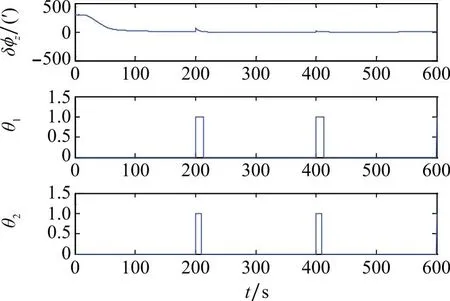
图10 试验3(UKF)Fig.10 Test 3 of UKF
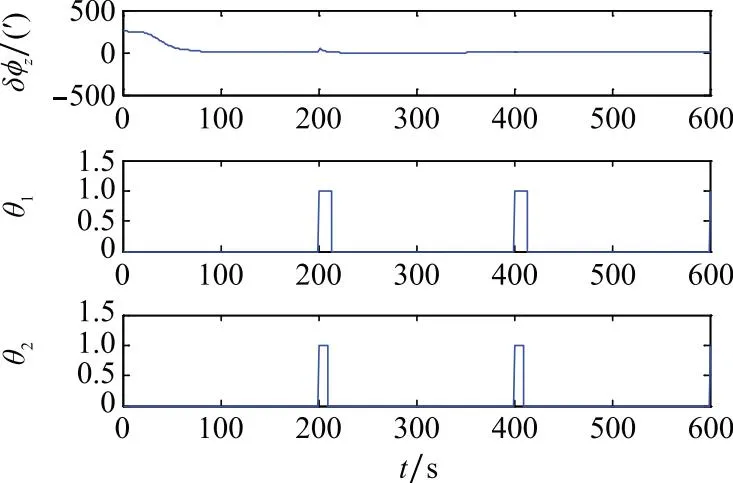
图11 试验3(CKF)Fig.11 Test 3 of CKF
图9~图11为第三组试验中两种判据的检验效果。在200 s、400 s和600 s 3个时间点上,两种判据均能检出突发的观测噪声异常,并且由检出异常的时间宽度可以看出,在严格程度上同样是判据1大于判据2。综合对比3组试验结果可以发现,在系统噪声异常情况下两种判据都存在一定的漏判,这是因为观测噪声对新息序列的影响更加直接,因此相比系统噪声而言,两种判据对观测噪声异常的检验更加准确。此外,由于异常噪声对滤波历史状态信息存在滞后影响,导致检测到异常的时间宽度大于实际异常的时间宽度,因此3组试验中都产生了一定的“拖尾”现象。
5 结 论
本文针对KF的异常检验问题,结合SINS初始对准的应用实例开展研究,从理论上分析了基于新息协方差匹配和基于卡方检验的滤波器异常检验判据,分别基于传统KF、UKF和CKF设计了滤波异常判据的验证试验,试验结果表明两种判据对滤波器系统和观测噪声异常情况都有一定的检验能力,且基于新息协方差匹配的异常判据的严格程度比基于卡方检验的异常判据的严格程度更高,但前者的拖尾效应因此更加明显。此外两种判据对系统噪声异常都存在一定漏检情况,而对观测噪声异常的检出效果更好。
通常在KF的自适应或强跟踪等优化研究中需要引入滤波器噪声参数的调谐操作,一方面增加了滤波算法的计算量,另一方面对最优递推过程的渐近稳定性产生干扰。因此,基于一定判断原则(而非无限制引入)的滤波器优化具有相当的必要性,在基于本文所述两种判据进行的滤波优化研究中,应结合优化方法的计算量负担并考虑其对正常滤波稳定性的干扰情况选择适合的异常检验判据,使优化方法的引入时机更加合理。对比来看,基于新息马氏距离的卡方检验判据存在概率约束,因此其对滤波异常的检验条件更加宽松。目前两种判据都无法区分系统噪声异常或观测噪声异常,即无法辨识噪声点的异常性质,而两种异常的优化策略通常不同,因此在下一步的研究工作中有必要研究更加灵活且具有针对性的异常定位方法。
