基于一致性理论和S-MPC的四旋翼编队协同避障

胡树欣, 张 安, 孙嫚憶, 李铭浩

(西北工业大学航空学院, 陕西 西安 710072)

0 引 言

多机编队协同控制研究已成为近年来无人机系统领域的一个前沿课题,文献[1-6]中提出一些具有代表性的编队控制方法,包括虚拟结构、行为和基于领航-跟随的编队控制方法。编队协同控制不仅可以发挥单架无人机具有的机动性能优势,还可以使多架无人机协同合作共同完成较为复杂的任务[7-12],是一种典型的多智能体系统[13],而这些协同控制任务的实现均建立在多智能体系统的一致性问题研究框架内。一致性理论的基本思想是编队中每架无人机都可以与其邻居无人机进行通信,通过设计一种分布式的算法使得无人机的状态变量达成一致[14],以此来实现无人机间的合作。

在无人机编队飞行中,安全问题是首要考虑的关键因素之一,避障研究就显得尤为重要。和单机避障相比,编队飞行不仅要考虑外部障碍,还需考虑内部的避碰、避障完成后队形的重构等问题[15]。文献[16]采用人工势场法,通过构造避障惩罚函数解决了多智能体的避障问题,并证明了算法的全局渐进稳定性和最优性,最后通过数值仿真实验验证了算法的有效性。但其没有考虑无人机的状态、输入约束等。文献[17]以一致性协议为基础构造时变编队,并通过设置虚拟领导者引导编队移动,避障方法采用人工势场法,通过数值仿真验证了时变编队飞行过程中避障算法的有效性。文献[18]基于速度障碍法将避碰、避障等问题转化为凸优化问题的约束条件,通过构建代价函数来求解最优控制输入,最终实现了三维环境中的多无人机局部运动规划、避碰和避障。文献[19]采用人工势场法,当两架无人机之间的距离小于给定值时,将人工势场力作为修正项添加到一致性算法中,在保证无人机内部避碰的前提下使一致性算法仍能收敛。但在使用人工势场法时,存在算法陷入局部最优解的问题,且在改变机群的编队队形时需要调整原有势场函数的参数大小,灵活性较低。文献[20]基于改进一致性算法设计无人机编队,在避障问题中分别引入粒子群算法和模型预测控制(model predictive control, MPC)算法来处理静态和动态障碍物,通过数值仿真验证了算法的有效性,但该算法缺少相关的稳定性和收敛性证明。

本文受文献[21-27]启发,针对无人机编队的队形生成、保持及静态障碍物避障问题,以一致性协议为基础构造编队控制器,通过设置领航者引导编队移动,避障方法采用安全攸关MPC(safety-critical MPC, S-MPC)算法,使得无人机能够在距离障碍物一定距离前对其进行规避,可有效避免在实际飞行过程中因反应时间不够而造成危险。最后,通过数值仿真实验验证了无人机编队飞行过程中躲避障碍物的能力。

1 问题描述

1.1 四旋翼无人机动力学模型

考虑存在一个由1架领航无人机和n架跟随无人机组成的四旋翼无人机编队系统,其中每架四旋翼无人机具有相同的运动特性,其结构形式如图1所示。

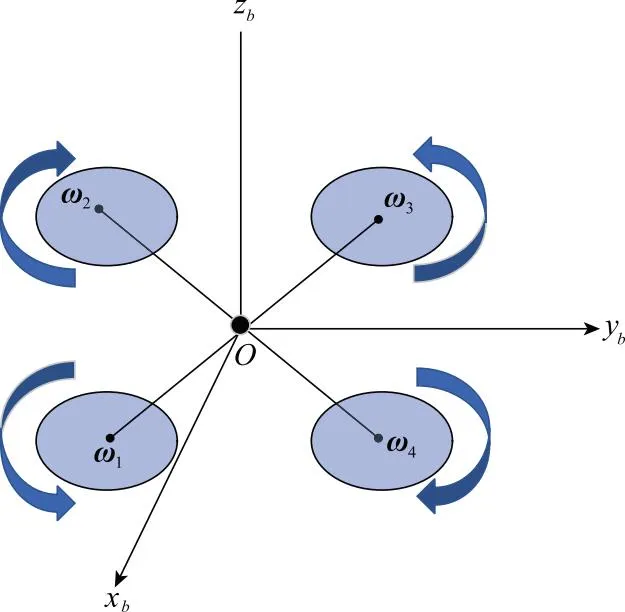
图1 四旋翼无人机结构图Fig.1 Structure diagram of quadrotor unmanned aerial vehicle

为了简化四旋翼无人机模型,做出如下假设:

假设 1四旋翼是刚体,其质量和转动惯量不变,几何中心与重心一致。忽略空气阻力的影响。

假设 2螺旋桨对推力指令的响应足够快,可以忽略从控制器向电机发出推力指令到螺旋桨产生实际推力的时间延迟。

假设 3在飞行过程中,偏航角始终不发生变化。

在以上假设的基础上,为简化系统模型,在定点悬停的平衡状态下,将非线性四旋翼模型进行线性化处理。简化后四旋翼系统动力学模型如下所示:

(1)

式中:k∈{1,2,3}分别代表x、y、z3个维度。3个方向上状态向量ξk、状态矩阵Ak、输入矩阵Bk和控制输入uk的具体形式如下:

(2)

(3)

(4)

(5)

表1给出了式(2)～式(5)的符号解释。

表1 控制输入和状态符号定义

在水平方向x,y上,模型组合后可表示为

(6)

式中:ξh和τ分别为水平面上的组合状态向量和组合控制输入向量,ξh的具体形式如下:

ξh=[s(0)T,s(1)T,s(2)T,s(3)T]T

(7)

式中:s(k)定义为组合向量,其表达式为

(8)

(9)

(10)

同样,用水平面上纵向控制输入τθ和横向控制输入τφ定义组合输入向量τ:

(11)

状态矩阵Ach和控制输入矩阵Bch分别表示为

(12)

式中:⊗表示Kronecker积;IN∈RN×N表示N维单位矩阵。

同时,高度方向状态空间模型可表示为如下形式:

(13)

式中:ξv=[z(0)z(1)]T=[z-w]T;f=ftotal/m;状态矩阵Acv和控制输入矩阵Bcv分别表示为

(14)

式(6)和式(13)中连续时间模型可离散化表示为

ξh(k+1)=Ahξh(k)+Bhτ(k)

(15)

ξv(k+1)=Avξv(k)+Bvf(k)

(16)

式中:k是一个非负整数,表示时间步长;t时刻仿真时间,表示为t=kΔt,Δt为仿真步长,同时:

(17)

(18)

1.2 图论基础

无人机编队系统的通信拓扑结构可以用图G=(V,E)来描述,其中V={1,2,…,n}表示图G中的节点集合;E⊆V×V表示边(i,j)的集合,其中i∈V,j∈V。用图G中的节点i代表编队系统的第i架无人机,边(i,j)∈E代表节点i能够获取节点j的状态信息,且称节点j是节点i的邻居。用Ni={j|(i,j)∈E}表示节点i的邻居集。若无人机i与j之间可双向通信,图G为无向图。其拉普拉斯矩阵定义为L=D-A。其中,D=diag{di}表示其入度矩阵,di为向节点i传输信息的节点数目,其形式如下:

(19)

A=[aij]表示其邻接矩阵;aij为边(i,j)的权值,可表示为

(20)

1.3 编队问题描述及求解框架

在本文中,考虑以下控制任务:n架无人机在三维空间中跟随其领航者编队飞行,同时避免碰撞。图2显示了4架无人机跟随领机编队飞行。其中,Leader表示领航无人机,Quadrotor 1～Quadrotor 4表示4架四旋翼无人机。

图2 编队控制问题描述Fig.2 Description of formation control problem

编队控制问题求解框架如图3所示,其中UAV1～UAVn表示第1架～第n架无人机,UAV(#1)～UAV(#n)表示无人机信息通信传输流。具体而言,每架无人机在避免碰撞的同时收敛到时变的期望位置。时变期望轨迹由顶层基于一致性理论的编队控制器产生。为了实现这一控制目标,做出以下假设:

假设 4每个无人机都必须连接到网络上的领导者,但并非所有无人机都与领导者有直接联系。

假设 5所有网络连接必须是双向的。

假设 6领导者的行动必须独立于无人机,也就是说,领导者的行动不受任何无人机的影响。

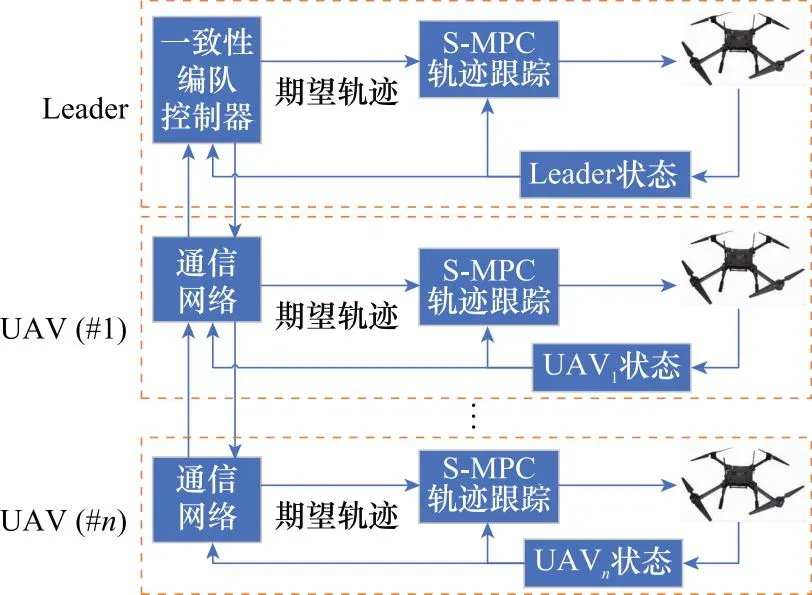
图3 编队控制求解框架Fig.3 Formation control solution’s framework

2 基于一致性理论的编队控制器

在领航-跟随控制策略下,基于一致性理论设计编队控制器。该控制算法的优点是,所有无人机都不一定需要直接连接到领航者,如果网络结构满足编队问题描述中的假设4～假设6,则无人机与其邻居通信就足够了。无人机i在水平面上编队飞行的控制律由式(21)和式(22)给出:

i∈{1,2,…,n};j∈{1,2,…,n+1}

αk>0, ∀k∈{0,1,2,3}

(21)

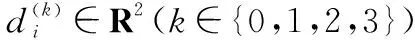
i∈{1,2,…,n};j∈{1,2,…,n+1}

βk>0,k∈{0,1}

(22)

以水平方向为例,为了得到各架无人机的期望状态轨迹,采用基于一致性的协同控制算法,即式(21)计算下一阶段的期望状态,并通过重复该过程生成预测时域内的期望状态。设Np∈R,Nc∈R分别为预测时域和控制时域。计算期望状态轨迹的控制算法如下。

算法 1 期望轨迹生成算法 步骤 1 获取当前状态通过网络获取每架无人机的当前状态ξhi(k)(i∈{1,2,…,n})。步骤 2 计算下一时刻的期望状态通过无人机当前状态,计算下一时刻水平方向上的期望状态ξrefhi(k+1)(i∈{1,2,…,n})。 ξrefhi(k+1)=Ahξhi(k)+Bhτi(k), i∈{1,2,…,n}式中:τi(k)为通过式(21)获得的水平方向的编队飞行控制输入。步骤 3 计算预测时域内的期望状态轨迹将从步骤2中得到的所需状态替换为当前状态。返回到步骤2,并在接下来的时间步长中计算所需的状态。重复这一过程,直到获得(k+Np)时刻水平方向上的期望状态。步骤 4 生成期望轨迹将预测时域内的期望状态组合如下:ξ～refhi=[ξTrefhi(k+1),ξTrefhi(k+2),…,ξTrefhi(k+Np)]T,i∈{1,2,…,n}

算法1根据无人机当前状态,生成各无人机预测时域内编队飞行期望状态轨迹。

3 基于S-MPC的避障控制

为了避免碰撞,通常采用的方法是为障碍物添加膨胀半径,这种做法实际上是等同于缩小了障碍物可行集的范围。这种基于欧几里得范数的避障约束并不会影响无人机的运动,并不能使无人机在比较远的距离就开始避障,在实际操作过程中常常会存在反应时间不够而造成的危险。通过模型预测控制,在确保集合不变性的前提下,将限制无人机运动加入到优化过程中。通过将控制障碍函数(control barrier function, CBF)添加到模型预测控制器的优化约束中,以保证MPC算法的安全性。下面将介绍二者的结合使用。

3.1 MPC

MPC是一种基于模型的控制方法,通过对系统动态模型的预测来生成控制策略,从而实现对系统的控制[28]。MPC将系统的控制问题转化为优化问题,通过对未来一段时间内的状态和控制变量进行预测,计算出满足约束条件的最优控制策略。随着预测时间步长的不断向前,MPC将不断更新控制策略,以实现系统的稳定性和最优性能[29]。

无论结构和形式如何,MPC一般都具有如下特点:预测模型、滚动优化和反馈校正[30]。由于模型预测控制具备上述特点,基于该算法的控制器可以取得较好的控制效果并且具有很强的抗干扰性能。MPC的控制原理如图4所示。

图4 MPC原理Fig.4 Principle of MPC

(23)

(24)

(25)

第i架无人机通过解决以下局部子问题,来跟踪水平方向上的期望状态轨迹。子问题描述如下:

(ξhi(k+Np)-ξrefhi(k+Np))+

(ξhi(k+j)-ξrefhi(k+j))+

(26)

式中:下标i∈{1,2,…,n}表示第i架无人机;Qi为非负定矩阵;Ri为正定矩阵。令Ξ=Ah+BhKh,终端权重Pi必须满足以下线性矩阵不等式(linear matrix inequality, LMI)以保证MPC的稳定性:

(27)

Pi>0

(28)

式中:Kh是一个状态反馈控制增益矩阵,用于在水平方向稳定无人机系统。子问题对状态和控制输入没有显式的不等式约束,以尽可能快地计算求解优化问题。图5是由4架无人机和领航者组成的多无人机系统通信网络结构。

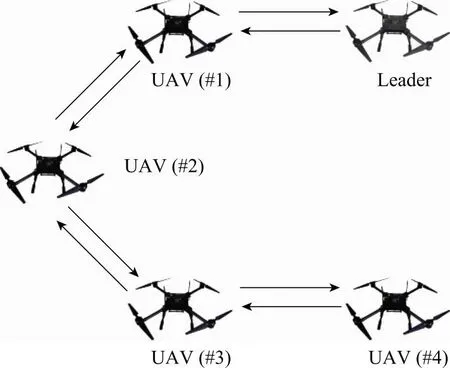
图5 编队通信网络结构Fig.5 Formation communication network’s structure

每个无人机执行的编队控制算法如算法2所示。

算法 2 编队飞行轨迹跟踪算法 步骤 1 当前状态的获取:获取当前状态ξhi(k)。步骤 2 信息传输:按照从领航者出发的通信网络拓扑结构,将信息传输给直接连接的无人机,直到领航者获得所有无人机的信息。某一无人机发送的信息由其自身的当前状态和其接收的信息组成。步骤 3 期望状态轨迹的生成:依据算法1的步骤2～步骤4,领航者计算每架无人机的期望状态轨迹。步骤 4 信息传输:按照与步骤2相反的顺序将信息传递给直接连接的无人机,该信息由期望状态轨迹和所有无人机的当前状态组成。步骤 5 优化求解:通过数值计算求解子问题的最优解τ～*i。步骤 6 施加最优控制输入:将最优控制输入序列τ～*i的第一个分量τ*i(k)作用于UAVi。步骤 7 重复步骤1～步骤6。

在步骤5中,每架无人机只解决自己的子问题以规划自己的行动,并且与其他无人机并行解决问题,而不是按顺序解决问题。这使得无人机的决策独立于其他无人机的决策。步骤2和步骤4中的步骤减少了通信的数量。由于无人机内嵌无线通信模块的可靠性较差,因此尽量减少无线通信的数量是非常重要的。

3.2 稳定性证明

定理 1假设一个多无人机系统包含n(n≥1)架无人机和一个领航者。同时,满足假设4～假设6。当每架无人机执行算法2时,若终端权重矩阵Pi满足式(27)和式(28),算法2中的MPC器将保证渐近稳定,无人机将收敛到水平方向编队飞行的期望状态。

证明由于子问题是一个凸二次规划(quadratic programming, QP)问题,因此其在任何时间步长都存在解。另外,当满足假设4～假设6时,领航者可以通过算法1生成编队水平方向飞行的期望状态轨迹。选用以下值函数作为Lyapunov函数:

(29)

(30)

因此,为了保证MPC的稳定性,需要有如下不等式成立:

ΔVi(k)=Vi(ξhi(k+1))-Vi(ξhi(k))<0

(31)

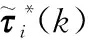
(32)

现在,考虑以下不是最优控制序列的控制输入:

(33)

式中:τi(k+Nc)是使无人机系统在水平方向稳定的控制输入。

当Kh是使无人机系统在水平方向稳定的状态反馈增益矩阵时,考虑将以下控制输入作为稳定的控制输入之一:

(34)

上述控制输入是虚拟的,并不将其作用于无人机系统。根据式(33)和式(34),式(32)可以改写为

(35)

τi(k)满足在预测时域内足够小,则表明:

ξrefh(k+Np+1)=Ahξrefh(k+Np)

(36)

由式(6)和式(36)可知,离散时间模型中变量ξh(k+Np)可表示为

(37)

由式(37),可将式(35)改写为

(38)

由于不等式的后两项总是负的,为使ΔVhi(k)<0,必须满足以下不等式:

(39)

Pi>0

(40)

系统的渐近稳定性可以用Lyapunov定理求解。因此,当k→∞时,UAVi的状态满足ξhi(k)→ξrefhi(k),这使得在水平方向上编队飞行收敛到所需的状态。

证毕

3.3 控制障碍函数

将离散时间CBF添加到MPC控制器的约束中处理安全性约束。对于安全性控制问题,定义在自由空间C(没有障碍物)中一个连续可微的函数h(χ):X⊂Rn→R,其中C为安全集:

C={χ∈X:h(χ)≥0}

(41)

函数h(·)即为CBF,同时有∀χ∈∂C,∂h/∂χ≠0,并且存在一个扩展的κ∞类函数γ(·),使得对于控制系统,h(·)满足:

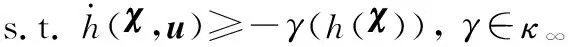
(42)

该条件可以扩展到离散时间域,如下所示:

Δh(χk,uk)≥-γ(h(χk)), 0<γ≤1

(43)

式中:Δh(χk,uk)=h(χk+1)-h(χk),将其代入式(44),可以得到h(χk+1)≥(1-γ)h(χk),即控制障碍函数h(·)的下限随着速率1-γ的值呈指数下降。

将CBF约束添加到优化问题中,得到:

(44)

式中:χ=[xy]T代表水平面上的位置向量。

4 仿真分析

4.1 避障控制仿真实验

在提出S-MPC控制设计的基础上,在二维平面内进行了仿真验证,并分析了其特性,采用IPOPT求解器解决S-MPC中的优化问题。

对于离散时间控制障碍函数约束,选择二次障碍函数:

(45)

式中:xobs、yobs、robs分别描述了障碍物的x、y的坐标和半径,障碍物信息如表2所示,障碍物在仿真图中用橙色圆圈所示。起始位置和目标位置分别为(-5,-5)和(0, 0),用黑色菱形标记。

表2 障碍物信息

(1) 参数γ对控制器的影响分析

在图6中,γ=0.1,0.2,0.5,1.0的S-MPC控制器规划的轨迹分别用红色、绿色、蓝色和紫色线表示。从图6可以看出,随着γ的降低,系统开始更早地避开障碍物,这意味着更小的安全集。图7、图8分别为不同γ参数值下S-MPC控制器每次求解优化问题的时间及其平均值。可以看出,γ参数并不会影响控制器的求解效率。

图6 不同γ参数下的S-MPC规划轨迹Fig.6 S-MPC planning trajectory with different γ parameters

图7 不同γ参数下的S-MPC每次迭代计算时间Fig.7 Calculation time of each iteration of S-MPC with different γ parameters

图8 不同γ参数下的S-MPC平均计算时间Fig.8 Average calculation time of S-MPC with different γ parameters

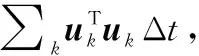
表3 参数γ影响分析

(2) 参数Np对控制器的影响分析

图9为不同预测时域Np下S-MPC控制器规划的轨迹。由图9可知,Np值对系统开始规避障碍物的远近并未产生较大影响。这是由于离散时间CBF强制了安全集的不确定性,它允许S-MPC具有较小的Np值,以实现与具有较大Np值的S-MPC相同的性能。图10、图11为每步的求解时间及其均值,可以看出,S-MPC的预测范围越小,计算时间越短。

图9 不同Np参数下的S-MPC规划轨迹Fig.9 S-MPC planning trajectory with different Np parameters

图10 不同Np参数下的S-MPC每次迭代计算时间Fig.10 Calculation time of each iteration of S-MPC with different Np parameters

图11 不同Np参数下的S-MPC平均计算时间Fig.11 Average calculation time of S-MPC with different Np parameters

(3) S-MPC预测性能分析

图12为存在3个障碍物的空间中,S-MPC控制器规划出的轨迹,当其中一个障碍物由(3,2)位置移动到(5,2)位置时,最优轨迹从左侧障碍物下方移动到左侧障碍物上方,这充分体现了S-MPC预测控制的特点。

图12 S-MPC轨迹规划Fig.12 S-MPC planning trajectory

(4) S-MPC避障能力分析

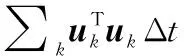
图13 S-MPC和APF规划轨迹Fig.13 S-MPC and APF planning trajectories

4.2 编队控制仿真实验

实验采用1架领航者(UAV5)和4架跟随者的编队机群,其通信拓扑结构如图14所示。各无人机的初始位置如表4所示。各参数设置为

(46)

图14 编队通信拓扑结构Fig.14 Structure of formation communication topology

表4 无人机初始状态

在一致性编队控制协议下,通过S-MPC跟踪顶层生成的期望轨迹,同时引导编队避障。无人机编队飞行轨迹如图15所示。从图15可以看出,仿真开始后,无人机编队基本在1 s内形成了预期的队形,并保持该队形飞行。在距离障碍物一定距离时,领航机提前引导编队对障碍物进行规避,且在过程中,编队队形只在小范围内调整,基本维持不变。

图15 无人机编队飞行轨迹Fig.15 Unmanned aerial vehicle formation flying trajectory

图16、图17分别给出了5架无人机的位置和速度曲线,从图16和图17可以看出,5架无人机基本在2 s内跟踪到了领航机的运动轨迹,形成了期望队形,随后保持编队系统位置和速度的一致性,完成了避障任务。图17中的速度曲线基本位于其约束集,满足状态约束。针对初始速度不满足约束等特殊情况,在S-MPC优化问题有解的前提下,通过施加状态软约束使速度曲线基本在1 s前进入约束集内。

图16 无人机编队系统位置跟踪一致性Fig.16 Position tracking consistency for unmanned aerial vehicle formation system

图17 无人机编队系统速度跟踪一致性Fig.17 Velocity tracking consistency for unmanned aerial vehicle formation system

5 结 论

本文针对无人机编队系统队形保持和避障控制问题,提出了基于S-MPC和一致性理论的分布式多无人机协同避障控制算法。在领航跟随策略下,设计基于二阶和四阶一致性的编队控制算法,为每架无人机生成期望轨迹。进一步地,通过在S-MPC算法中引入CBF约束,实现了编队系统对障碍物的较早规避,规划轨迹满足状态约束,且更为平滑,使飞行能量损耗更少。最后,进行无人机编队避障飞行仿真实验。仿真结果表明,本文所提出的控制算法具有较好的控制效果,能够有效规避外部障碍。

本文编队飞行仅在二维平面进行障碍物规避,并未考虑三维环境下的协同避障问题。后续将结合无人机轨迹规划设计的方法,实现无人机编队的三维避障飞行控制。