过载和攻击时间约束下的非线性最优制导方法

2024-01-30段欣然

系统工程与电子技术 2024年2期

王坤, 段欣然, 陈征,2,*, 黎军,2

(1. 浙江大学航空航天学院, 浙江杭州 310027; 2. 浣江实验室, 浙江诸暨 311800)

0 引言

各类目标的逃逸和防御能力不断提升,导致某些情况下导弹需以特定时间击中目标才能实现有效毁伤。例如,在攻击配备近程防御武器系统的目标时,多弹以期望时间同时抵达目标被认为是饱和其防御能力的一种有效方式[1-2]。另外,在攻击或拦截具有逃逸或躲避能力的时敏目标时,导弹需在特定时间窗口抵近目标。制导律作为导引和控制导弹飞向目标的核心算法,直接决定其抵近目标的时间。为此,在过去的几十年里,国内外学者对时间约束下的制导律进行了广泛的研究。

Jeon等[3]在文献中提出了一种能够控制攻击时间的制导算法(impact time control guidance, ITCG);该算法在比例导引(proportional navigation, PN)的基础上增加了一个偏置项,并通过剩余飞行时间的估计值和期望值之间的偏差来调整偏置项的大小,进而控制攻击时间。文献[4]基于PN的解析解将ITCG进行扩展,使得其可用于运动目标的拦截问题。文献[5]设计了一种具有时变导引系数的PN方法,实现了多弹攻击时间的协调控制。文献[6]基于最优误差动力学方法,将制导律设计视为有限时域内的攻击时间误差调节问题,根据攻击时间误差设计了反馈指令,通过施瓦兹不等式求解线性二次型最优控制问题,实现了对于攻击时间的控制。文献[7]将最优误差动力学方法推广于导弹速度变化条件下的时间控制问题。文献[8]基于PN提出了一种虚拟领导者方案来控制攻击时间。文献[9]基于剩余飞行时间的显式表达式提出了一种导引系数时变的时间控制算法,进一步提升了剩余飞行时间估计值的精度,且该算法适用于导弹速度变化和三维场景。

除了上述基于PN的时间约束制导方法外,还有一些方法也被用于攻击时间的控制问题,如滑模控制技术[10-15]、李亚普诺夫稳定性理论[16]、弹道成型方法[17-18]、矢量制导[19]、前置角跟踪方法[20]、二次规划[21]等。这些方法适用于约束条件更为复杂的场景,如具有攻击角度和/或视场角约束的场景[22-25]。然而,这些方法一般不考虑性能指标的最优性,可能导致导弹在飞行过程中动能损失过大[26],进而影响攻击效果。此外,其中一些方法依赖于对剩余飞行时间的估计,在小角度假设不成立的条件下存在时间约束难以精确满足、制导精度低等问题[27-28]。

实时在线求解攻击时间和导弹动力学等非线性约束下的最优控制问题是克服上述不足的一种有效方法,且该方法一般被称为非线性最优制导(nonlinear optimal guidance, NOG)[29]。在非线性约束条件下,最优控制问题的实时在线求解是弹道力学与制导领域的公认难题。因此,国内外学者一般在各种简化或线性化基础上建立最优控制问题的解析解或半解析解。例如,Chen等[27]提出了一种参数化方法,使得可通过求解非线性方程来确定NOG。Merkulov等[28]应用二阶泰勒展开多项式近似导弹的非线性运动学方程,得到了攻击时间约束下NOG的半解析解。Guelman等[30]围绕目标运动轨迹可预测情况下的拦截问题,将相关NOG问题转换为求解三维非线性方程组的问题。一般来讲,通过求解非线性方程零点而生成最优制导指令时,存在收敛时间长、甚至不收敛的问题,尚不能从理论上确保在线生成最优解的收敛性和稳定性[31]。此外,也有学者尝试用优化方法解决 NOG问题。例如,Liu等[32]通过将非线性最优控制问题转化为二阶锥规划问题,利用内点法求解NOG。由于NOG问题所对应的非线性规划问题可能存在多个局部最优解,利用优化方法也不能确保制导指令的最优性,如本文数值仿真部分(第3.1节)所示。

为了解决实时在线生成NOG指令的问题,Wang等[26]通过引入文献[33]所建立的哈密尔顿轨迹参数化方法,对具有攻击时间约束的NOG问题进行了参数化处理,保证通过简单数值积分即可生成飞行状态到制导指令的单一、最优映射关系的数据。根据通用近似定理[34],具有单一、最优特征的数据集能够从理论上确保前馈神经网络近似飞行状态到最优制导指令映射关系的收敛性和准确性,最终利用前馈神经网络实现了最优制导指令的实时在线生成。但是,文献[26]未考虑过载约束。实际上,对于无动力导弹,其侧向过载常因结构和气动因素而受到一定约束。不考虑过载约束而设计最优制导律,可能导致制导指令的不稳定[35]。为此,本文在文献[26]的基础上,进一步对过载约束下的NOG指令实时在线生成问题展开研究。

一些学者已经对过载约束下的制导律进行了研究。Rusnak等[36]在线性化条件下推导出了输入受限时最优制导律的显式解。Hexner等[37]采用线性二次随机高斯最优控制理论推导了过载限制下的最优制导律。其他过载限制下的制导律设计方法包括动态面控制[38]、滑模控制[39]等。然而,针对过载和攻击时间等约束下的NOG(overload-and impact time-constrained NOG, OTNOG)问题的相关研究还较为鲜见。

为了解决过载和攻击时间约束下的最优制导指令在线生成问题,本文首先将制导问题构建为具有输入和时间约束的非线性最优控制问题,并采用庞特里亚金极大值原理(Pontryagin’s maximum principle, PMP)推导出最优轨迹的必要条件,并引入饱和函数消除了最优制导律中的输入约束。在此基础上,本文基于文献[33]提出的哈密尔顿轨迹参数化方法积分生成最优轨迹,从而建立飞行状态到最优制导指令映射关系的数据集。根据通用近似定理[34],利用前馈神经网络对上述数据集中的状态-最优制导指令之间的映射关系进行了近似,实现了过载和时间约束下的NOG指令的毫秒量级在线生成。最后,通过数值仿真验证了本文所提方法的有效性。

1 数学模型

(1)

式中:t为时间;“·”表示关于时间的导数。

图1 导弹和目标的几何关系Fig.1 Interception geometry for the missile and target

令

σ=λ-θ+π

则式(1)在极坐标系中可写为

(2)

对于式(1)的动态系统,最小化控制能量为

(3)

考虑如下输入(导弹侧向过载n)饱和约束:

|n|≤nm

式中:nm>0为过载上限,且侧向过载与侧向加速度满足如下关系:

式中:g为重力加速度,取值为9.81 m/s2。为方便处理,将侧向过载约束转换为侧向加速度约束,即

|u|≤um

(4)

式中:um=g·nm。另外,导弹初始条件为

x(0)=x0,y(0)=y0,θ(0)=θ0

(5)

终端条件为

x(tf)=0,y(tf)=0

(6)

式中:终端时间(期望攻击时间)tf为固定值。

2 最优轨迹数据集的生成方法

2.1 最优性条件

令px,py,pθ分别表示x,y,θ所对应的协态变量。根据PMP[40],哈密尔顿函数可表示为

则协态方程为

(7)

最优控制律为

(8)

由于末端速度方向角自由,则有如下横截条件:

pθ(tf)=0

(9)

根据式(7),可得常数px和py。考虑终端边界条件式(6)和式(9),并对式中的第3个等式进行积分,可得

pθ(t)=V(pxy(t)-pyx(t)),t∈[0,tf]

(10)

定义如下饱和函数:

sat(z,ε,η,δ)=

(11)

式中:z是函数输入;ε是已知下限;η是已知上限;δ是保证饱和函数处处可导的光滑因子。因此,式(8)中的最优控制律可写为

(12)

对于足够小的δ>0,式(8)可由式(12)无限逼近,详细证明参见文献[41]中的引理2。

如果(x(t),y(t),θ(t))在区间t∈[0,tf]满足式(7)～式(10)中的必要性条件,则将其称为一条哈密尔顿轨迹[33]。根据文献[42],上述必要不充分条件尚不能保证哈密尔顿轨迹的最优性。利用引理1,将建立最优轨迹需满足的附加最优性条件。

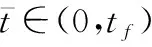
(13)

则在[0,tf]内的哈密尔顿轨迹(x(·),y(·),θ(·))不是最优轨迹。该引理的证明详见文献[26]。下文将利用PMP和引理1中的最优性条件建立哈密尔顿轨迹的参数化微分方程组。

2.2 哈密尔顿轨迹的参数化微分方程组

对于任意给定协态变量px,py,令

定义常数β∈[-π,π],使其满足:

px=αcosβ,py=αsinβ

(14)

则可将式(10)改写为

pθ(t)=Vα[y(t)cosβ-x(t)sinβ]

(15)

定义如下参数化微分方程组:

(16)

式中:(X,Y)∈R2,且Θ∈[0,2π]。对于t∈[0,tf],定义(X(t,α,β),Y(t,α,β),Θ(t,α,β))∈R2×[0,2π]为参数化微分方程组的解,且令其初始状态为(0,0,0)。显然,对任意α>0和β∈[-π,π],有

(X(0,α,β),Y(0,α,β),Θ(0,α,β))=(0,0,0)

易知对于t∈[0,tf],结合式(13)所得到的(X(t,α,β),Y(t,α,β),Θ(t,α,β))均满足最优轨迹的最优性条件。

2.3 飞行状态到最优制导指令的映射关系

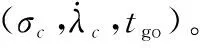
得益于引理1和第2.2节中建立的参数化微分方程组,导弹在tgo∈(0,tf]时的状态可表示为(X(tgo,α,β),Y(tgo,α,β),Θ(tgo,α,β))。令f:[-π,π]×R×(0,tf]→R表示状态与最优制导指令之间的映射关系,即

由图1的几何关系和最优轨迹的最优性条件可知f可由式(17)建立:

(17)

根据文献[26]中的引理3,为了生成最优轨迹簇,只需考虑σc在半开区间(0,π]的取值。定义:

(18)

为通过参数化微分方程组进行积分而得到的状态-最优制导指令映射关系f的数据集。

对于给定时间间隔t∈(0,tf]和(α,β),在区间(0,tf]对参数化微分方程组进行积分后可得到一条最优轨迹,对其进行离散即可获得状态与最优制导指令之间映射关系的一组数据集Fp。定义一个空集D,对(α,β)进行遍历,将获得的Fp插入到D,即可获得供前馈神经网络近似的数据集D。

3 数值仿真

对于特定导弹,其速度和过载约束已知。设导弹的飞行速度为250 m/s,过载约束为±5。则方程中的参数化系统可由δ,(α,β),tf来表示。设tf=40,δ=5,α在[0,10]以0.05 s为间隔均匀取值,β在[-π,π]以0.03 s为间隔均匀取值。根据上述参数取值情况,对方程中的参数化系统进行数值积分,共可得到40 401条最优轨迹。从每条最优轨迹中以间隔0.1 s均匀离散得到Fp,然后将其插入到训练数据集D中。

利用全连接前馈神经网络近似D中包含的映射关系f。将D以70/15/15的比例拆分为训练/验证/测试集。将传递给神经网络的输入和输出均通过减去平均值、除以标准差的方式进行归一化。选择Sigmoid函数作为激活函数,隐含层设为3层,每层包含30个神经元。输出层使用线性函数。将训练的损失函数设为神经网络的预测值与D中的真实值之间的均方误差(mean square error, MSE)。训练完成后,训练、验证和测试集的MSE均降至2.115 1×10-7。为了便于表达,将上述由哈密尔顿轨迹参数化和神经网络相结合得到的NOG生成方法称为OTNOG。下文将对OTNOG的实时性和最优性进行仿真验证。

3.1 制导指令的实时性和最优性仿真验证

为了验证实时性,在基于ARM Cortex-A7内核、主频为528 MHz的工业级CPU上对NOG指令的生成时间进行了测试,单次运行时间为0.60 ms,满足各型制导飞行器对在线生成制导指令的实时性需求。下面将通过与优化方法对比而验证OTNOG的最优性。

考虑3枚导弹对一固定目标进行协同打击的场景,将每枚导弹的初始位置和速度方向角取值列于表1中,设置期望攻击时间为40 s。

表1 导弹初始条件

在OTNOG导引下的飞行轨迹如图2(a)中绿色虚线所示。图2中,Mi(i=1,2,3)表示第i枚导弹初始位置,T表示目标位置。为展示协同打击效果,PN(导引系数为3)导引的导弹飞行轨迹如图2(a)中红色点画线所示;成熟的最优控制求解软件GPOPS[43]在求解第2枚导弹的打击问题时不收敛,未能得到飞行轨迹。为了进一步对比,采用间接法中的打靶法进行求解,得到的轨迹如图2(a)中的蓝色实线所示。

图2 实时生成最优制导指令仿真结果Fig.2 Simulation results for generating the optimal guidance command in real time

从图2(a)可以看出,与PN相比,OTNOG由于需要满足打击时间约束而产生了更为弯曲的飞行轨迹,尤其是第2枚导弹。具体而言,第1枚导弹在PN导引下需要30.119 6 s抵达目标位置,第2枚导弹需要29.298 2 s,第3枚导弹需要38.112 0 s,而OTNOG导引下的3枚导弹均在40 s命中目标。对于第1枚和第2枚导弹,OTNOG和打靶法所得到的飞行轨迹几乎重合,而对于第3枚导弹,OTNOG和打靶法得到了截然不同的飞行轨迹。需要强调的是,即使打靶法能够得到最优轨迹(如图2(a)所示,打靶法和OTNOG都得到了第1枚和第2枚导弹的最优轨迹),但是打靶法较为耗时,不能满足实时性的要求。相比而言, OTNOG不仅能够满足实时性要求,还可保证最优性。

另外,OTNOG和打靶法所给出的制导指令和前置角变化曲线如图2(b)和图2(c)所示。令飞行过程中所消耗的控制能量为

(19)

则OTNOG和打靶法对应的控制能量如表2所示。从图2(b)可以看出,OTNOG和打靶法针对第1枚和第2枚导弹所给出的制导指令基本吻合,打击过程消耗的控制能量也非常接近。而对于第3枚导弹,OTNOG和打靶法所得到的制导指令存在较大区别,且OTNOG所得到的控制能量小于打靶法的控制能量。从图2(c)可以看出,对于第3枚导弹,打靶法所对应的前置角σ在3.13 s时达到了0°;根据引理1可知,基于优化方法的打靶法所得到的轨迹并不是一条最优轨迹。另外,打靶法所需的平均计算时间为1.89 s。

表2 OTNOG和打靶法对应的控制能量

3.2 典型制导方法的仿真对比

考虑导弹和目标的初始位置分别为(0,0)m和(2 500,0)m,导弹的初始速度方向角为70°,期望攻击时间为35 s。利用变系数PN(varying gain PN, VGPN)制导律[9]、非奇异终端滑模(nonsingular terminal sliding mode, NSM)制导[10]等典型制导方法进行对比验证。

本文将VGPN导引系数设置为3,其他参数与文献[9]保持一致,仿真结果如图3中的蓝色实线所示。当NSM的参数与文献[10]相同时,无法计算出可行解。为此,将文献[10]中NSM的导引系数从3调整为2后,得到了一个可行解,仿真结果如图3中的绿色点画线所示。相比于VGPN和NSM,OTNOG无需制导律参数设置,仿真结果如图3中的红色虚线所示。

图3 不同制导律的仿真结果Fig.3 Simulation results of different guidance laws

具体而言,图3(a)为不同制导律对应的飞行轨迹,图3(b)为不同制导律对应的制导指令。显然,由VGPN和NSM在导弹发射后产生的制导指令均达到饱和状态,导致前置角快速增加,如图3(c)所示。值得注意的是,VGPN和NSM均需对剩余飞行时间进行估计,因此需要主动式导引头实时提供弹目距离,以作为制导律的输入;相比而言,OTNOG所需的剩余飞行时间则由期望攻击时间简单地减去当前时间而得到。为方便比较,将攻击过程中的弹目距离变化曲线在图3(d)中进行展示。从图3(d)中可以看出,VGPN和NSM导引下的导弹在发射一段时间后快速远离目标。产生上述现象的主要原因是VGPN和NSM的制导指令与剩余飞行时间估计值有关,当剩余飞行时间估计值与真实值误差较大时,会产生较大过载以减小误差。相比之下,OTNOG在导弹发射一段时间后所给出的制导指令未达到饱和,所对应的前置角和弹目距离均缓慢增加。

在控制能量方面,从图3(b)可以看出,VGPN在导弹发射后前期的制导指令较大,整个攻击过程中的控制能量为2.195 2×104m2·s-3;对于NSM,其制导指令在相当长的一段时间内处于饱和状态,导致其所消耗的控制能量较高,达到了2.661 0×104m2·s-3,而且由于将PN系数调整至2,其末端制导指令无法收敛至零。相比之下,OTNOG所产生的控制能量为1.702 7×104m2·s-3,与由GPOPS[43]得出的最优解1.702 0×104m2·s-3非常接近,且末端制导指令收敛至零。

3.3 移动目标攻击的仿真验证

本文建立的OTNOG的输入仅包含视线角变换速率、前置角和期望攻击时间。因此,其也可用于移动目标攻击的场景。

3.3.1 匀速移动目标

图4 导弹和匀速移动目标的轨迹Fig.4 Trajectories of the missile and constant-moving target

图5 攻击匀速移动目标的制导指令Fig.5 Guidance command profile against the constant-moving target

图4为导弹和目标的飞行轨迹和运动轨迹,由图4可以看出导弹成功命中目标,由目标运动导致的攻击时间与期望时间的偏差为0.015 6 s。导弹的制导指令如图5所示,由图5可以看出制导指令在攻击前期较为平滑,随后达到饱和状态,当弹目距离较小时,OTNOG产生的制导指令出现了一定程度的波动,这是因为导弹与目标较为接近时,两者之间的前置角突然增加,导致制导指令波动。另外,OTNOG所产生的最大制导指令为48.949 3 m/s2,表明未破坏过载约束,且消耗的控制能量相对较小,仅为1.757 8×104m2·s-3。

3.3.2 机动目标

基于案例1的方法,利用OTNOG对速度为15 m/s、过载机动为2cos(0.2t)m/s2的目标进行攻击。设目标初始位置为(0,0)m,初始速度方向角为180°;导弹从(2 000,0)m的初始位置发射,初始速度方向角为90°,期望攻击时间为40 s。与案例1一致,OTNOG在剩余飞行时间达到0.2 s后切换为PN。

图6为导弹和目标的轨迹,从图6可以看出导弹的飞行轨迹为了满足较大的攻击时间约束而呈现出了较为弯曲的趋势;导弹最终以0.018 1 s的攻击时间误差命中目标。OTNOG在导引导弹过程中所生成的制导指令如图7所示,从图7可以看出,制导指令在攻击末端出现了多次波动。这是因为当导弹接近机动目标时,两者之间的相对方位关系迅速变化,导致OTNOG产生的制导指令快速变化。此外,由于期望攻击时间较长,在整个攻击过程中,OTNOG所产生的制导指令未出现饱和,且消耗的控制能量较小,仅为1.516 1×104m2·s-3。