基于能力的国防资源分配方法
2024-01-30张玉婷杨镜宇
张玉婷, 杨镜宇
(1. 国防大学研究生院, 北京 100095; 2. 海军参谋部机要局, 北京 100841;3. 国防大学联合作战学院, 北京 100091)
0 引 言
资源分配问题源于经济学,旨在将有限的资源,如人力、物力等,通过一定的规则分配给众多对象,进行资源优化配置,以提升经济效益。作战体系结构复杂、规模庞大,在有限的国防预算约束下,对其进行资源分配及统筹规划是体系建设发展中的一项重要内容,对于提升国防资源利用率、提高军事效益、形成强大的军队战斗力具有重要的现实意义。
现实生活中,各行各业都存在资源分配问题,许多学者也进行了一定程度的应用研究,并取得了一些成果。文献[1]提出了一种与资源管理相关的混合整数非线性数学模型,为救灾行动等不确定场景下的资源分配选址问题提供了帮助。文献[2]针对土地资源分配问题,根据当前政策和未来趋势,构建“粮食-水-能源”关系框架,对光伏产量、可行性、利润、生物质产量进行了全面评估。文献[3]基于“灰色-自回归移动平均模型”算法,构建改进的集装箱维修费用分配模型。文献[4]在贪婪调度算法的基础上,研究下一代光学数据中心网络资源调度问题,引入并行技术,加快了资源调度速率。文献[5]为高通量多波束通信卫星系统构建资源分配模型,并通过遗传算法对模型进行求解。文献[6]基于改进萤火虫优化算法,对云计算中的动态资源分配问题进行了研究,提出一种基于负载平衡优化的改进Firefly算法,提高了资源利用效率和生产力。文献[7]为武器装备经费分配问题构建数学规划模型,并通过差分进化方法求解模型。文献[8]使用机器学习算法预测了医院每日急诊就诊资源分配策略。文献[9]对战争不确定因素下的国防和民用支出资源分配问题进行了研究。文献[10]通过引入Agent构建优化框架,为解决军事规划中的成本效益优化问题提供了思路。文献[11]围绕战略管理环节评估,提出一种资源配置需求的形式化描述和探索性方法。文献[12]利用强化学习的方法,设计了一种基于异步深度强化学习算法的资源分配方法,实现了资源的自动规划。文献[13]开发了一种通过统计矩传播不确定性的方法,优化了建模和分析中的系统资源分配方案。文献[14]给出了一种基于Web的实时资源分配工具,辅助指挥员完成复杂的资源分配和运输任务。
可见,当前资源分配问题的研究思路和方法众多,且在军事方面已有学者研究了火力资源分配、装备经费分配、卫星资源分配等[15-20]相关问题,但对于联合作战体系建设发展层面的资源分配问题尚缺乏具体的模型和算法。
本文从体系建设发展的顶层设计角度出发,借鉴“基于能力的规划(capability-based planning, CBP)”[21-22]思想,在国防预算的约束下,通过分析各体系能力需求,构建体系资源分配的数学规划模型,并采用遗传算法对模型进行求解,得到体系建设发展的帕累托最优资源分配方案及体系总能力最大值。
1 基于数学规划法的国防资源静态分配模型
1.1 问题描述
体系建设发展中基于能力的国防资源分配问题可描述为:在一个五年规划内,在总预算B有限的约束下,以体系能力C作为输入,如何对N种不同类型的体系/系统进行合理的资源配置,达到预算最低、体系总能力最高的目标。基于能力的国防资源分配问题如图1所示。
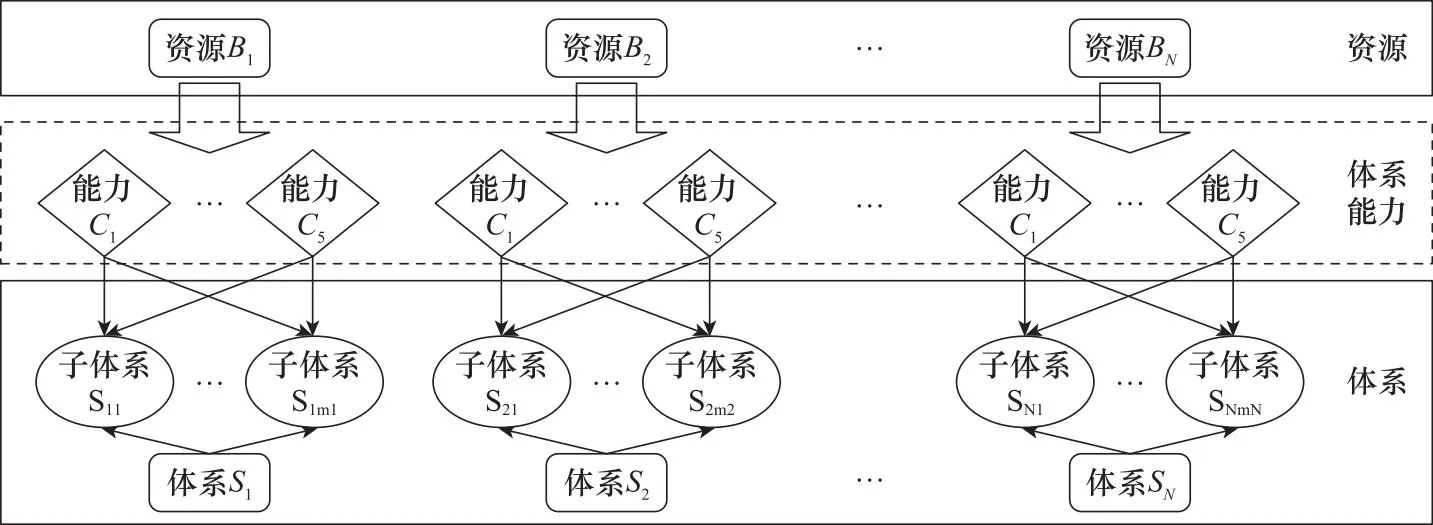
图1 基于能力的国防资源分配问题Fig.1 Capability-based defense resource allocation problem
1.2 符号和决策变量说明
(1) 对建模将用到的符号做出如下说明
B: 表示一个五年规划的总预算;
δ: 表示年度费用允许的波动范围,单位为%;
Si: 代表一级体系,i∈I=(1,2,3,…,n),n表示一级体系个数;
Sij: 代表二级体系,j∈J=(1,2,3,…,mi),其中mi表示第i个一级体系下的二级体系个数;
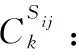
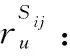
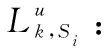
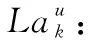
αSi: 表示第Si个体系的能力权重系数;
βk: 表示第k个能力的权重系数;
γu: 表示第u年能力的权重系数。
(2) 对建模的决策变量做出如下说明
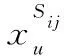
1.3 基于数学规划法的资源分配模型
1.3.1 条件声明
(1) 假定能力生成过程为理想化的累积生成过程,所有种类的能力构成体系总能力。
(2) 假定能力值为标量值,具备可加性。
(3) 假定国防经费在一个五年规划内按年度平均分配。
(4) 假定在一个五年规划内,每个二级体系仅有一次建设发展机会,即选择五年内的某一年进行发展。
1.3.2 模型构建
针对体系建设发展中的国防资源分配问题,采用数学规划法构建模型。
(1) 目标函数:体系建设发展的体系总能力达到最大值
(1)
(2) 约束1: 所有体系的实际建设发展费用不超过总预算
(2)
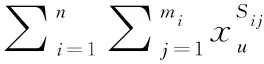
(3) 约束2: 年度经费平均分配,且在允许范围内波动
i∈I;u∈U;j∈J
(3)
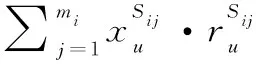
(4) 约束3: 一级体系对应的能力加权和满足最低需求
u∈U;k∈K;i∈I;j∈J
(4)
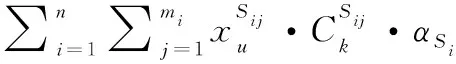
(5) 约束4: 五年规划内的第u年,所有体系对应的k种能力加权和满足最低需求
u∈U;i∈I;j∈J;k∈K
(5)
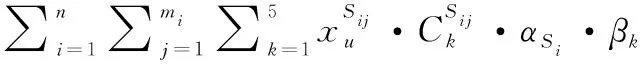
(6) 约束5: 一个五年规划内,每个二级体系仅发展1次
(6)
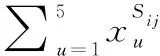
2 基于遗传算法的模型求解算法
2.1 遗传算法
遗传算法是Holland[23]受自然进化理论启发而提出的一种搜索算法,是启发式算法的一种,通过模仿自然选择和繁殖过程,进行染色体选择、交叉、变异等运算,并不断迭代寻找问题的全局最优解。相比传统搜索和优化算法,遗传算法有许多优点,如能够高效处理参数规模大、数学表达式复杂等问题。遗传算法的流程如图2所示。
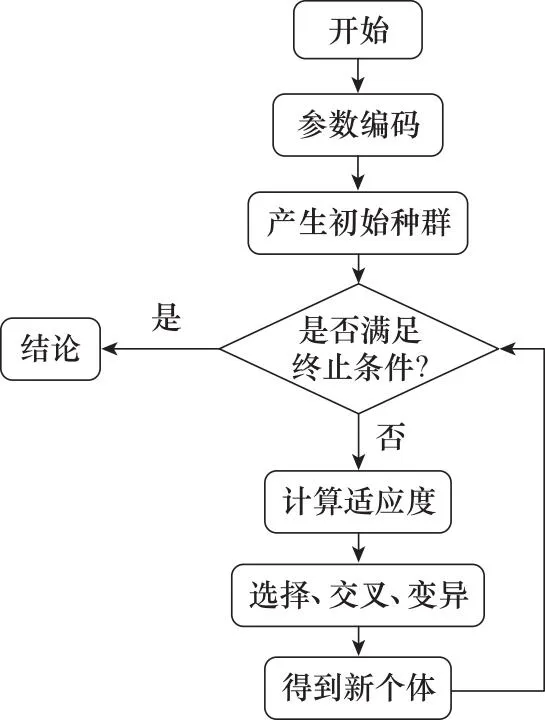
图2 遗传算法流程图Fig.2 Flowchart of genetic algorithm
国内外学者运用遗传算法解决了许多现实问题。文献[24]提出一种基于遗传算法的增强型资源分配算法,实现了云数据中心资源的高效分配。文献[25]设计了一种具有调度规则和双亲进化的改进遗传算法,有效逼近了网络效用和收敛速率。文献[26]基于遗传算法开发了一种可靠的柔性供应链网络设计模型,能够在一定程度上增强战略能力。文献[27]针对颌面部弹性体颜色配方问题,通过遗传算法开发了一种临床应用程序,辅助临床医生制定颜色并降低成本。文献[28]对P2P网络借贷问题进行了研究,运用遗传算法优化了传统网贷预警模型,提升了预警效果。文献[29]采用遗传算法,对数据预处理过程的特征选择和特征提取步骤进行了改进。
本文提出的国防资源分配模型中的数学表达式复杂,用传统算法求解较困难,容易导致组合爆炸,因此本文采用遗传算法进行编程,进行模型求解。为了使算法与模型较好地融合,对遗传算法进行相关设计,如确定初始种群、确定适应度函数、确定终止条件,进行编码和解码、选择、交叉、变异等。
2.2 编码和解码
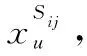
(7)
考虑到约束5,每个二级体系仅能发展1次,故可以使用实数编码,将决策变量中的参数u转换为1-5的实数,即针对一个二级体系,分配一个1-5的实数决定其在哪一年进行发展,于是决策变量个数可缩小至之前的20%。
2.3 求解步骤
步骤1确定初始种群
初始种群是种群迭代的基础,其数量不能过少或过多,否则容易陷入局部最优或增加计算难度。此处设定初始种群规模为200。
步骤2确定适应度函数
通过适应度函数能够判断染色体的优劣,本文将目标函数映射为适应度函数进行评估,即体系总能力最大为目标函数,目标函数值越大,适应度越大;反之亦然。
步骤3选择
选择算子指从群体中选择优秀个体、淘汰劣质个体,使得有用的遗传信息保留下来,提高收敛性。其过程需要根据由适应函数得到的适应度值的大小来实现,即不断选择优秀基因进行遗传,从而完成种群迭代。本文采用较常用的轮盘赌法进行选择操作,即个体被选择的概率与个体的适应度有关,适应度越高的个体被选择的概率越大,适应度越低的个体被选择的概率越小。被选择的个体进一步进行遗传操作。
步骤4交叉
交叉算子是遗传算法的核心,指由父代个体形成新个体的操作,其过程需按规定选择交叉点,以及交换交叉点的基因片段。本文采用的交叉策略为两点交叉和均匀交叉两种方式结合的交叉。
两点交叉指在父代中随机选择两个位置进行交叉,若父代1=1-2-3-4-5-4-3-2-1-2,父代2=5-5-5-5-4-5-4-3-2-1。假设选择的交叉点位置为2和4,则子代1=1-5-5-5-5-4-3-2-1-2,子代2=5-2-3-4-4-5-4-3-2-1;均匀交叉是个体中各个位置的基因都以相同的概率参与交叉,即在每个基因位置上都进行判定,如果随机数的大小满足概率要求,则该位置进行交叉,否则判定下一个交叉位置。
步骤5变异
变异算子指替换父代染色体基因片段,产生新的子代染色体序列。本文采用的变异方法为单点变异,即在满足变异概率的前提下,随机选择一个变异位置,将其基因随机转换为1-5的值。变异操作后应计算父代、子代染色体的适应度,若子代较优,则变异成功,父代由子代替换;若父代较优,则变异失败,继续迭代,直至满足终止条件。
步骤6确定终止条件
进化次数限制、计算资源限制、最优解限制、适应度限制等均可设置为终止条件。本文设置迭代次数为10 000,通过不断迭代达到预设的迭代次数并得到最优解时,结束迭代,输出迭代结果。
3 示例分析
以某个五年规划中的联合作战体系建设发展资源分配问题为例进行示例分析。
3.1 参数设置
对模型中的参数做如下设置:
假设 1一个五年规划内,年数u=5,总预算B=10亿元。
假设 2年度费用允许的波动范围δ=0.3。
假设 3需建设的一级体系的数量n=4,每个一级体系下的二级体系的数量mi=[10,12,14,13]。
假设 4考虑5种体系能力,p=5。
假设 5能力权重系数设置为
αSi=[1.1,1.2,1.3,0.9]βk=[0.89,0.9,1.0,1.05,1.1]γu=[0.05,0.1,0.15,0.3,0.4]
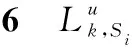
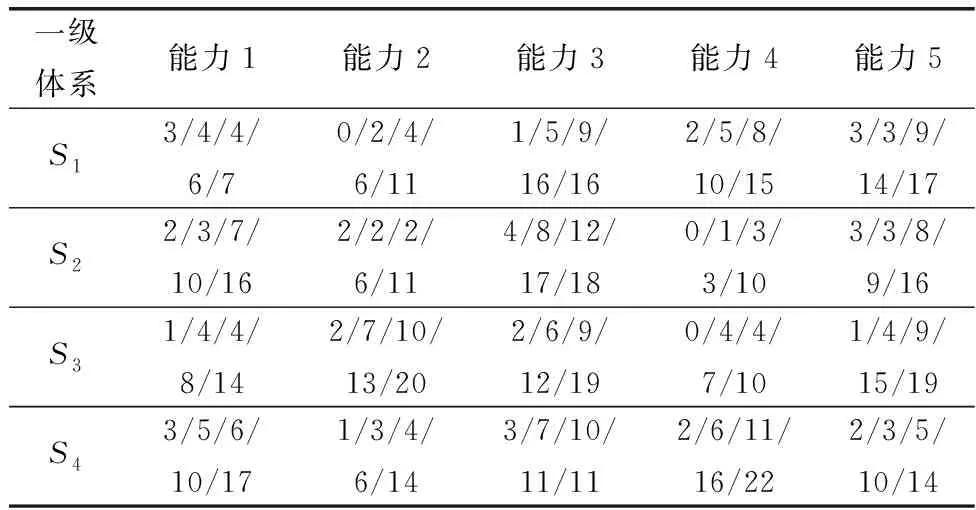
表1 每种能力最低需求
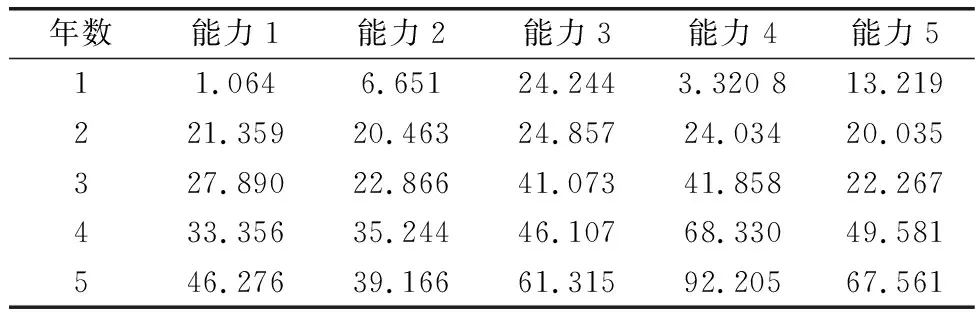
表2 每年每种能力加权和最低需求
3.2 结果分析
设置初始种群规模为200,迭代次数为10 000,利用算法迭代求解模型,输出一个五年规划内每个二级体系Sij得到发展的年份,如表3所示。
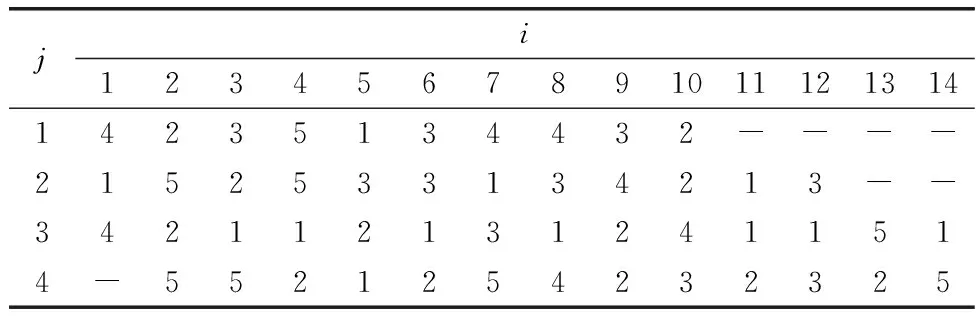
表3 二级体系发展年份
可见,每个一级体系对应的二级体系在一个五年规划内分别发展一次,表格中数字代表得到发展的年份。输出模型求解迭代图如图3所示。
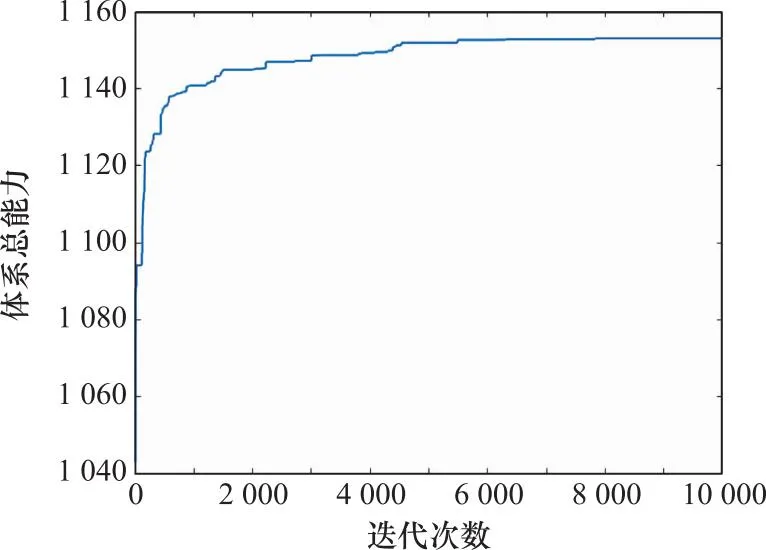
图3 模型求解迭代图Fig.3 Iterative diagram of model solution
由图3可知,当种群迭代至大约5 500次后,目标函数值保持不变,得到帕累托最优解,即体系总能力最大值。输出一个五年规划内每个二级体系每年的实际发展费用,如表4所示。
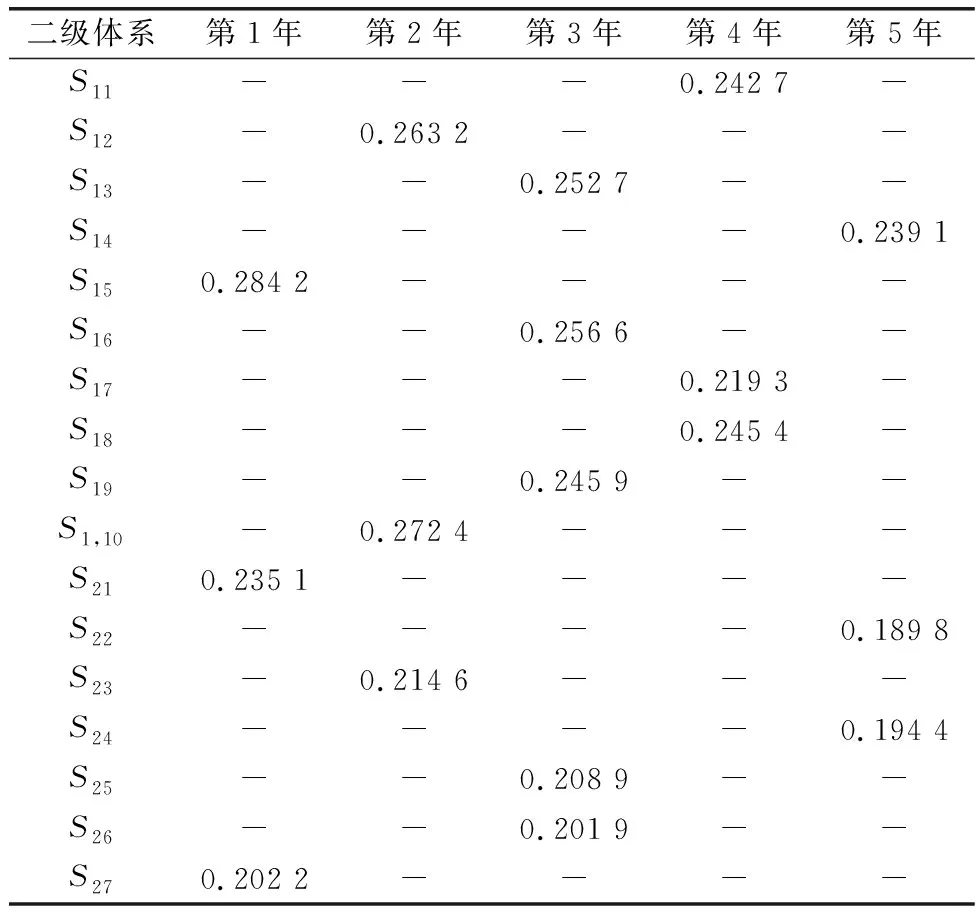
表4 二级体系发展费用
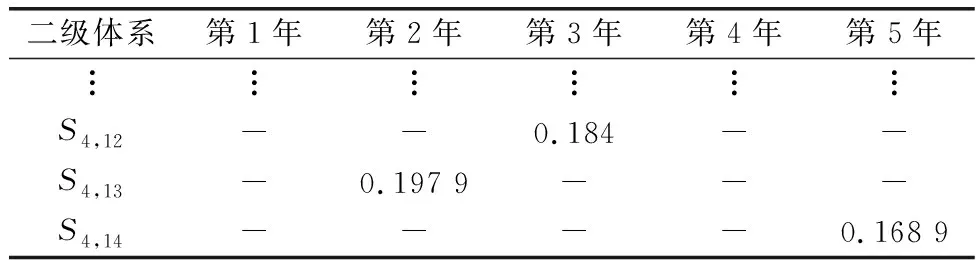
续表4
可见,设置的49个二级体系在其对应的年份内均得到发展。输出一个五年规划内每个一级体系每年的发展费用,如表5所示。
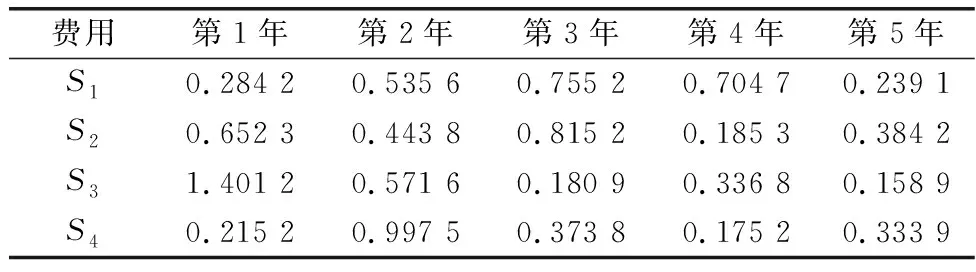
表5 一级体系每年的发展费用
综上所述,该示例结果表明,在一个五年规划内,在达到总能力最大目标的同时,体系建设发展的总费用为9.744 6亿元,未超出总预算10亿的约束范围,因此通过该示例能够验证所提方法的正确性与可行性。
4 结 论
资源分配是联合作战体系建设发展中的重要问题,合理配置资源、实现资源有效利用,对于提高军事能力意义重大。本文采用数学规划的方法,基于体系能力对联合作战体系资源分配问题构建模型,并运用遗传算法重复迭代、求解模型,得到模型的帕累托最优解,通过示例验证了所提方法能够完成五年规划内的国防资源统筹分配,进一步支撑联合作战体系建设发展的顶层规划。
