二分图匹配模型下的武器目标分配问题

吕 娜, 王茂桓, 钟元芾, 张英朝, 孙 蕾

(中山大学系统科学与工程学院, 广东 广州 510275)

0 引 言

武器目标分配(weapon target assignment, WTA)是军事运筹学领域经典的组合优化问题,其研究的是如何将武器合理分配给对方目标,从而实现理想的作战打击效果。近年来,作战指控人机结合程度不断提高,现代军事对抗需要指挥员在人工智能的辅助下更快、更好地做出决策,这对人工智能在复杂多变的战场态势下的求解能力提出了要求。对于WTA问题,这种求解能力体现在模型和算法对最优解的搜索能力和求解速度两个方面。

WTA问题的求解难点在于随着武器和目标数量的增加,分配方案的数量将呈指数级增加。Lloyd等[1]证明了WTA问题是一个多参数、多约束的整数规划问题,是非确定性多项式(non-deterministic polynomial, NP)完全问题,这意味着目前没有一个确定性算法能在多项式时间内找到问题的最优解。

Manne[2]于1958年提出WTA问题的数学模型,并对其进行线性近似求解。至今,WTA问题的算法研究一直是热点问题之一。根据优化方法的迭代方式不同,求解WTA问题的算法可以分为精确算法和近似算法[3]。使用精确算法如Soland[4]研究了用隐枚举和分支定界方法求解保护目标的反导弹防御问题。Sikanen[5]提出使用动态规划的方法求解小规模的WTA问题,提高了求解效率和解的质量。Kim等[6]采用拉格朗日松弛法对问题进行改造,将目标函数分解为3个子问题后进行求解,在一些问题上能够找到边界解。Lu等[7]在求解大规模WTA问题中引入了分配上下界,确定了武器支配关系,缩短了列枚举和分支定界的求解时间。使用近似算法如Wang等[8]通过结合编码方法和局部搜索算法,提出了离散的灰狼优化算法,适用于不同规模的WTA问题。Chang等[9]对动态WTA问题采用了改进的人工蜂群优化算法,并在种群初始化中引入启发式因子,提高了求解精度。Kong等[10]提出了改进的多目标粒子群优化算法解决多目标的动态WTA问题,得到的解具有更好的收敛性和分布性。Huangfu等[11]在模型中考虑自适应分组和视场角约束,再采用带有精英保留策略的遗传算法求解最优分配问题,证明了该算法求解具有较好的鲁棒性。也有部分学者将精确算法与近似算法结合,Ahuja等[12]先借用分支定界算法确定问题下界,再提出了基于网络流的构造式启发算法和大规模邻域搜索方法,实现了对不同规模武器资源的合理分配。常雪凝等[13]将模拟退火(simulated annealing, SA)算法与匈牙利算法结合,求解多阶段WTA问题,在保证求解质量的同时减少了求解时间。Leboucher等[14]先使用匈牙利算法求解武器与目标的分配对,再使用遗传算法与粒子群算法的混合算法求解分配的发射顺序。由上述研究可以看出,当前算法在兼顾WTA问题求解的准确性和高效性上有待进一步提高[15]。

近年来,图论在网络通信、线性规划等优化领域中应用广泛,使用基于图论的建模方法求解实际问题往往能够简化模型,降低计算复杂度,因此,图论受到众多研究者的青睐。其中,基于图论的二分图匹配建模方法常用于任务分配和调度等优化问题。Huo等[16]从二分图匹配的角度提出了云工厂间的协作模型,在Kuhn-Munkres(简称为KM)算法下可以求出高效的协作策略。Wang等[17]用二分图匹配辅助空间全卷积网络进行红外小目标检测。Man等[18]在大数据任务的人机协同问题上应用二分图最优匹配算法,提高了计算机资源的利用率。Chen等[19]利用二分图匹配提高了自动分配网络请求与服务的准确性。Ma等[20]将二分图匹配用于个人社交网络账号匹配,具有更高的准确率。Sun等[21]在三维模型的视图检索中应用了二分图匹配方法,有效提高了三视图与模型匹配的效率。Hashemi等[22]在图像的多标签特征选择问题中使用二分图匹配,提高了分类的准确性。Beiranvand等[23]提出在图像的无监督特征选择上采用二分图匹配建模,提高了图像特征选择的有效性。综上所述,对实际问题进行二分图建图,再使用二分图匹配模型求解,是一种有效的求解思路。

基于图论基础,本文创新性地提出一种精确求解WTA问题的求解框架:首先,使用二分图匹配建模方法,构建了WTA的二分图匹配模型。其次,提出一种改进的Kuhn-Munkres WTA(简称为KM-WTA)算法,用于对目标模型进行求解。该框架巧妙地利用了WTA问题中主体的可分离性,简化了原WTA模型中目标函数非线性带来的难点。同时,KM-WTA算法可以在对WTA问题进行精确求解的基础上,进一步提升计算速度。对于战场这种强对抗性和复杂多变的应用环境,本文提出的求解框架具有更好的求解效率和可解释性。

本文的结构安排如下:第1节在简要介绍相关图论基础后,提出了基于二分图匹配的WTA模型,并对模型进行优化;第2节给出了结合贪心策略的KM-WTA算法,以及相应的求解流程;第3节通过仿真实验验证模型和算法的有效性,并对本文算法和其他算法的计算能力进行分析对比;第4节对全文做出总结,提出了对WTA问题的研究展望。

1 基于二分图匹配的WTA模型构建

由于WTA问题是多项式复杂程度的非确定性(non-deterministic polynomial, NP)完全问题,传统的精确算法计算时间太长,以元启发式算法为代表的近似算法求解精度又无法保证。本文提出基于二分图匹配,对WTA问题构建模型,可以将模型自然简化为无约束规划问题。

1.1 图论基础

图论[24]是研究离散对象间关系的一个数学分支,图论中的图并不只局限于描述几何中的图像,某些具体事物及其之间的联系也可以抽象为图,这种图一般由一些点和点之间的连线构成。在图中,将这些点叫做顶点,将顶点间的连线叫做边,一般顶点的集合用V表示,边的集合用E表示,因此图G可以简记为G=(V,E)。而二分图是图论中一种特殊的模型,若简单图G的顶点集合可以分为两个互不相交的非空集合V1和V2,使得图G中每一条边与其关联的两个顶点分别在X和Y中,则称图G为一个二分图,记作G=(X,Y,E)。若X中的每个顶点与Y中的每个顶点相关联,且只与Y中的顶点相关联,则称该图为完全二分图。一个简单的完全二分图如图1所示。

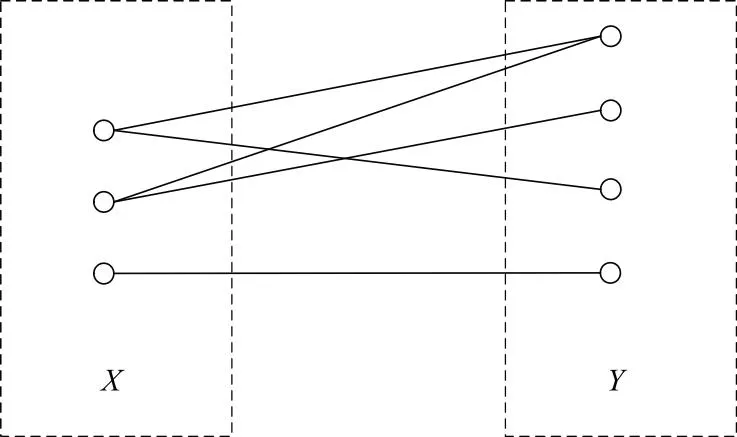
图1 完全二分图Fig.1 Complete bipartite graph

从图G=(V,E)的边集E中选取一个子集M,若M中任意两条边互不相邻,则称M是G的一个匹配;若对图G的任何匹配M′,均有|M′|≤|M|,则称M为G的最大匹配。进一步地,若图G是二分图,可以表示为G=(X,Y,E),且其中X的每一个顶点都与M中的一条边相关联,则称M是二分图G的完全匹配。特别地,当|X|=|Y|时,M是G的完美匹配。考虑一个加权的完全二分图G=(X,Y,E,W),其中X={x1,x2,…,xt},Y={y1,y2,…,ys},W=(wij),i=1,2,…,t,j=1,2,…,s,表示边xiyj的权重,满足匹配中所有边权之和最大的匹配M即为最优匹配。

1.2 问题分析与建模

WTA问题假设现有己方武器m个,需要在较短时间内完成对n个对方目标的打击,每个目标的威胁程度记为vj;Pij表示己方武器i对目标j的毁伤效率。WTA问题要确定的是武器与目标间的分配关系,使作战打击后对方目标对己方可产生的威胁程度最小化。

WTA问题与二分图模型的对应关系如图2所示。参与分配的主体可以明确分为两类,己方武器集合W和敌方目标集合T,等价于完全二分图G=(X,Y,E,W)中的两个独立点子集X和Y。武器与目标之间的连线代表了不同武器打击不同目标的毁伤效率,在二分图中体现为X与Y之间有权重W的边集E。

图2 WTA问题与二分图的对应关系Fig.2 Corresponding relationship of WTA problem and bipartite graph

基于二分图匹配的WTA模型构建的核心在于决策变量的转换。传统的WTA问题的变量是m×n个0-1决策变量Xij,Xij取值为1时代表将武器i分配给目标j,否则武器i与目标j之间没有打击关系,在确定所有打击关系后再计算总体威胁,得到目标函数值。而基于二分图匹配的WTA模型将目标威胁的计算提前到决策变量的确定阶段,先计算每个目标分别被每个武器打击后的威胁,将其作为加权二分图的权重,接下来只需要选择E的子集M,并对M中的边权求和,即可得到目标函数值。

1.3 符号说明和假设

为了便于模型的描述与分析,相关的参数和变量说明如表1所示。

表1 参数与变量符号说明

同时为了便于模型求解,本文提出以下假设:

假设 1在求解过程中,目标和武器数量均已知并不会发生变化。

假设 2每个武器对每个目标的毁伤概率已知。

假设 3每个武器只打击一个目标,每个目标也只被打击一次。

1.4 数学模型构建

由于本文所构建的模型是通过将武器分配打击目标,尽可能减少对方可能造成的威胁,下面给出了以最小化对方目标被打击后的总体威胁程度为优化目标函数的数学模型:

(1)

wij=vj(1-Pij)

(2)

M={xiyj|Xij=1}

(3)

(4)

(5)

Xij∈{0,1},∀i∈{1,2,…,m};∀j∈{1,2,…,n}

(6)

模型中,式(1)为目标函数,表示所有目标被打击后的总体威胁程度;式(2)～式(6)为约束条件,其中式(2)表示目标j被武器i打击后的威胁程度,式(3)表示集合M由具有打击关系的边构成,式(4)和式(5)约束了每个武器只打击一个目标,且每个目标只被打击一次,式(6)是0-1决策变量约束。

1.5 模型优化改进

考虑到二分图匹配问题的特殊性,为了便于进一步求解,对上述数学模型提出进一步优化改进。

(1) 根据第1.1节中匹配的定义,匹配中的任意两条边都不相邻,因此当集合M是一个匹配时,自然满足了上述模型中的式(4)和式(5),即每个武器打击一个目标且每个目标只被一个武器打击。

(2) 为了便于应用二分图匹配模型的算法求解,需要满足条件|X|=|Y|,于是本文提出了一种补全方法,如图3所示。当武器数量与目标数量不等时,通过补全矩阵使对应二分图的边权矩阵为方阵。

以图3为例,当武器数(m=4)大于目标数(n=3)时,增加(m-n)个虚拟目标,在边权矩阵中增加(m-n)列,其中每一列取值均为0(由于虚拟目标并不存在实际的威胁)。若最后得到的匹配中包含某条边顶点为该虚拟目标,则表示这条边上的相应武器不需要打击。当武器数(m=3)小于目标数(n=4)时,增加(n-m)个虚拟武器,在边权矩阵中增加(n-m)行,其中每一行的第j个值为vj(虚拟武器对目标没有毁伤概率)。若最后得到的匹配中包含某条边顶点为该虚拟武器,则表示这条边上的相应目标未被打击。

图3 边权矩阵的补全Fig.3 Completion of margin weight matrix

最后,由于通常完全加权二分图最优匹配所求得的是具有最大权的匹配,而WTA问题的目标是最小化函数值,因此对上述矩阵W取相反数,即可将其转化为最大化问题。

综上所述,本文提出的模型式(1)～式(6) 可以进一步简化为

(7)

(8)

式中:a=max{m,n};M是完全二分图G=(X,Y,E,W)的一个匹配。

2 KM-WTA求解算法

KM算法是求解二分图最优匹配的经典算法,但在大规模匹配问题中,该算法计算效率太低。为提高算法求解不同规模问题的速度,本文将在求解加权完全二分图的最优匹配的KM算法的基础上求解WTA问题,下面首先对KM算法的原理和算法流程进行介绍,再提出对该算法的改进和相应的计算流程。

2.1 KM算法原理

KM算法是由Kuhn和Munkres提出的在加权完全二分图中求取最优匹配的有效算法[24]。算法采用给图中顶点赋值的方法,即图论中的可行点标号,从图中任一顶点开始赋值,使得一条边上的两个顶点被赋值之和恰好等于边权(即相等子图)。在该相等子图中用匈牙利算法寻找最大匹配,若该匹配恰好是完美匹配,那么该匹配就是待求问题的最优匹配;否则需要对可行点标号进行更新再重复上述过程,直至找到最优匹配。

KM算法的步骤如下。

步骤1以任取的可行点标号l作为开始,确定l相等子图Gl,且在Gl中选取任一匹配M。

步骤2从M出发,利用匈牙利算法求相等子图Gl的最大匹配M′。若M′是完美匹配,则M′就是最优匹配,计算结束;否则,进入步骤3。

再返回步骤1。

KM算法的流程图如图4所示。

图4 KM算法流程图Fig.4 Flowchart of the KM algorithm

其中,匈牙利算法是二分图求最大匹配问题的经典算法之一,由匈牙利数学家Egervary提出。这一算法基于Berge匹配定理,对于任意一个二分图G,从任意一个匹配M开始,通过寻找M的非饱和点,并确定M可扩路取对称差的方法,对匹配M进行扩充,直到不存在M可扩路为止,届时已找到G的最大匹配。对于满足|X|=|Y|的加权完全二分图,该最大匹配也是完美匹配。

2.2 KM-WTA算法及其流程

在实际应用中,WTA问题具有极高的时效性,如果求解过程耗时太久,则有可能导致结果与战况不匹配。因此,该分配问题对算法求解速度有更高的要求。本文在KM算法中引入了贪心策略,能够有效减少计算量,加快计算速度。KM-WTA算法的流程图如图5所示。

图5 KM-WTA算法流程图Fig.5 Flowchart of KM-WTA algorithm

首先,根据贪心策略获得初始可行点标号:分别令子点集X中点的初始可行点标号为以该点为端点的所有边中的最大权重值,同时选择每个点对应的权重最大的边组合成为初始边集合M0,这样减少了随机确定初始可行点标号和由初始匹配导致的计算量增加。

其次,依次判断初始边集合M0中的每条边能否加入匹配M,如果M中的边一直互不相邻,则可以继续添加;若出现两边相邻的情况,则不满足匹配的定义,需要根据贪心策略调整可行点标号,选择权值最大且满足相等子图条件的边加入匹配。这种方法与根据匈牙利算法寻找可扩路并确定最大匹配相比,计算更加简单高效。

引入贪心策略的KM算法伪代码如算法1所示。

算法 1 KM-WTA算法输入 武器数量m、目标数量n、毁伤效率矩阵P、目标威胁向量v输出 最优匹配M并根据式(7)计算相应的目标函数值01 根据第1节中的式(8)计算边权矩阵02 初始化:l(xi)=maxj=1,2,…,n(wij),i=1,2,…,m,l(yj)=0,j=1,2,…,n,每个点对应的权重最大的边组合成为初始边集合M0,初始匹配M=⌀,记与M中的边相连的点集与子点集X的交集为P,与子点集Y的交集为Q03 for i=1:m04 if与xi相连的点yj不与M中的边相邻05 M=M∪{xiyj}06 Break07 else更新可行点标号08 d=min(l(xp)-w(xpyq')),其中xp∈P,xq'∈Y-Q09 l(xp)=l(xp)-d,l(xq)=l(xq)+d,其中xp∈P,xq∈Q10 连接可行点标号更新后的匹配11 返回04重新判断12 end13 end

2.3 改进算法的复杂度分析

下面对该改进算法的计算复杂度进行分析。

从时间复杂度来看,根据上述算法流程可以看出,在贪心初始化的前提下,只需对点子集X中的点进行讨论,若记a=max{m,n},遍历子集中所有点需执行a次计算;在每次计算中,在最好的情况下,不需要对可行点标号进行调整,权重最大的边可以直接列入匹配M,只嵌套了两层循环,时间复杂度为Ο(a2);在最差的情况下,需要对可行点标号进行调整,对相邻边连接的点子集X中的点重新进行检查,相当于嵌套三层循环,时间复杂度为Ο(a3)。

从空间复杂度来看,在算法执行过程中,需要6个大小为a的向量空间,其中2个用于记录可行点标号,4个用于记录检查匹配关系,其余为一些常数值的记录,尽管算法过程中有循环,但并不需要占用额外的计算空间,因此计算的空间复杂度为O(a)。

综上所述,该算法的计算复杂度不高,可以在短时间内快速准确求解。

3 仿真实验验证与分析

3.1 实验结果

为验证本文所提出的模型与算法的有效性,在运行环境为Windows 11系统,AMD Ryzen9 5950X 16-Core处理器,32GB运行内存的计算机上进行实验分析。

由于WTA问题目前尚未形成一致的基准问题数据集,因此本文实验在20个不同维度的问题上进行,武器对目标的毁伤概率由在0.6～0.9内均匀分布的随机数生成,目标的威胁程度由在25～100内均匀分布的随机数生成。其中,WTA1～WTA12问题借鉴了文献[25]中的问题实例,毁伤概率矩阵和目标的威胁向量也采用文献[25]中的设置,每个问题的武器数与目标数相等。WTA13～WTA20问题的毁伤概率矩阵和目标威胁向量按上述规则随机生成,为体现第1.5节中二分图权重向量补全的方法,每个问题武器数与目标数之比分布在[1/4,4]范围内。20个问题的维度如表2所示,其中WTA1、WTA2、WTA13和WTA14属于小规模实验,WTA3～WTA10和WTA15～WTA20属于中等规模实验,WTA11和WTA12属于大规模实验[3]。

表2 问题维度

将本文提出的模型与算法简记为KM-WTA,使用该算法对上述实例问题求解。为了保证算法的有效性,每个问题的实验结果取10次计算的平均值,并记录每次计算的平均运行时间,如表3所示。

表3 实验结果与运行时间

续表3

从表3中可以看出,KM-WTA算法运行时间很短。按问题规模来看,在小规模和中等规模问题中,大多数问题运行时间都不超过1 s,在大规模问题中运行时间也不超过30 s。按武器与目标数量之比来看,在小规模问题上,武器与目标数量不等,比同等规模的武器数与目标数相等的问题求解时间更长。通过对比WTA1与WTA13和WTA14可以看出,原因是当问题规模不大时,由补全图的权重矩阵导致的计算时间延长。而在大规模问题上,当武器与目标数量不等时,相比同等规模的武器数与目标数相等的问题求解时间更短,通过对比WTA9与WTA18和WTA20看出,原因是补全的权重矩阵中有大量0元素,减少了计算时间。

3.2 实验对比

本节主要围绕本文提出的模型算法与其他模型与算法在相同数据下的实验结果对比展开。下面依次进行不同模型求解结果的对比、KM-WTA算法与KM算法的求解结果对比,以及改进KM-WTA算法与并行SA(parallel SA, PSA)算法[25]和改进的乌鸦搜索算法(modified crow search algorithm, MCSA)[26-27]的求解结果对比和分析。

3.2.1 不同模型对比

传统WTA数学模型可以表示如下:

(9)

(10)

(11)

Xij∈{0,1},∀i∈{1,2,…,m}; ∀j∈{1,2,…,n}

(12)

其中,式(9) 为非线性目标函数,表示每个目标被打击后的存活概率,其与相应的目标威胁程度相乘后求和,得到所有目标总体威胁程度;式(10)和式(11) 表示武器与打击目标间的一一对应关系;式(12) 表示决策变量约束。

为了验证本文对WTA模型改进的有效性,用式(9)～式(12)基于20组实验数据进行求解,计算求解器选择“Optimization Toolbox”中的“fmincon”函数,计算结果见表4中“FMINCON”所在行的数值。由于该求解器的计算原理为分支定界算法,属于精确算法,因此多次计算结果都相同,略去中位数、平均数以及标准差部分,仅计算时间取10次计算的平均值,运行时间超过3 600 s的视为未能得到计算结果,记作“-”。

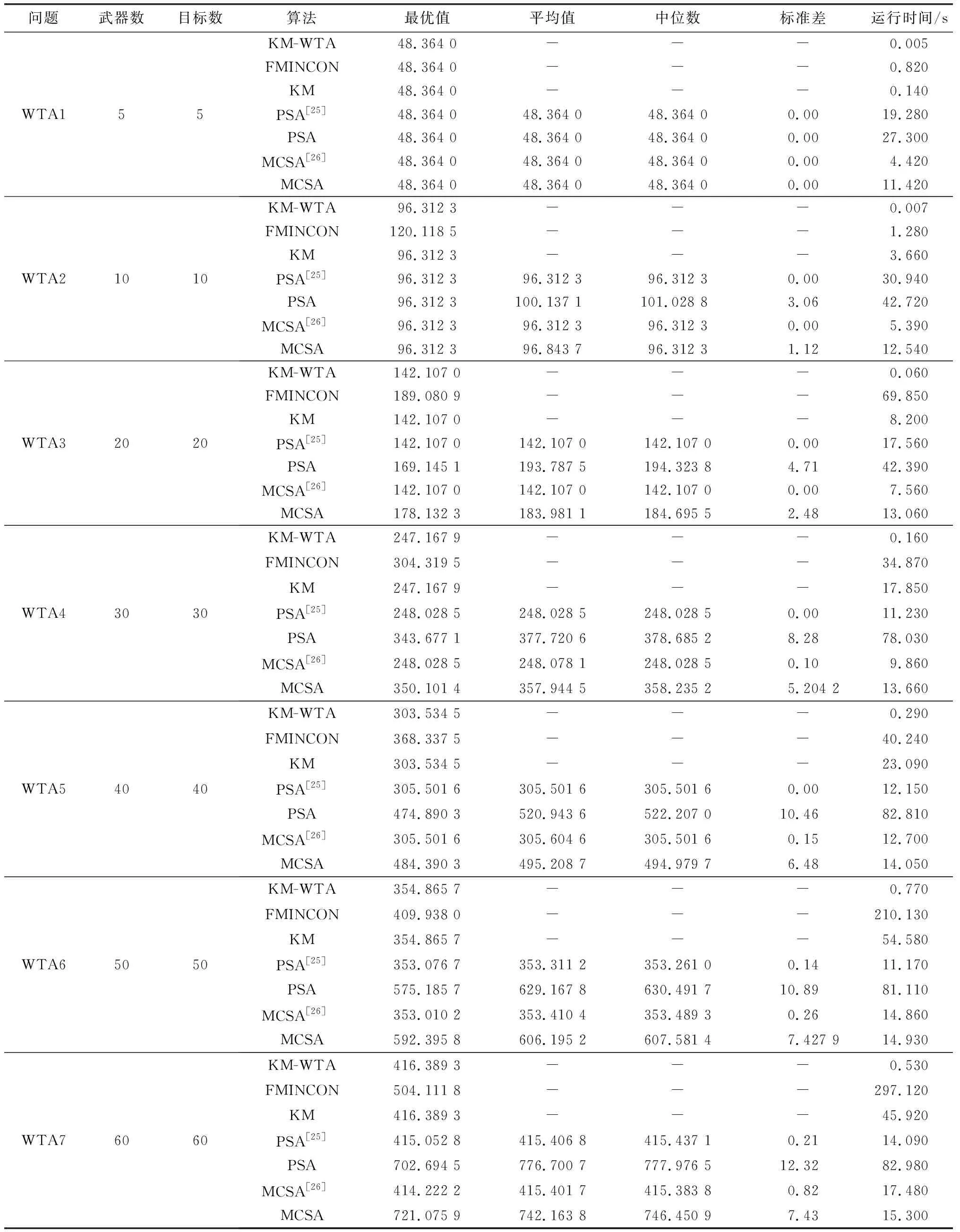
表4 多种算法实验结果对比

续表4

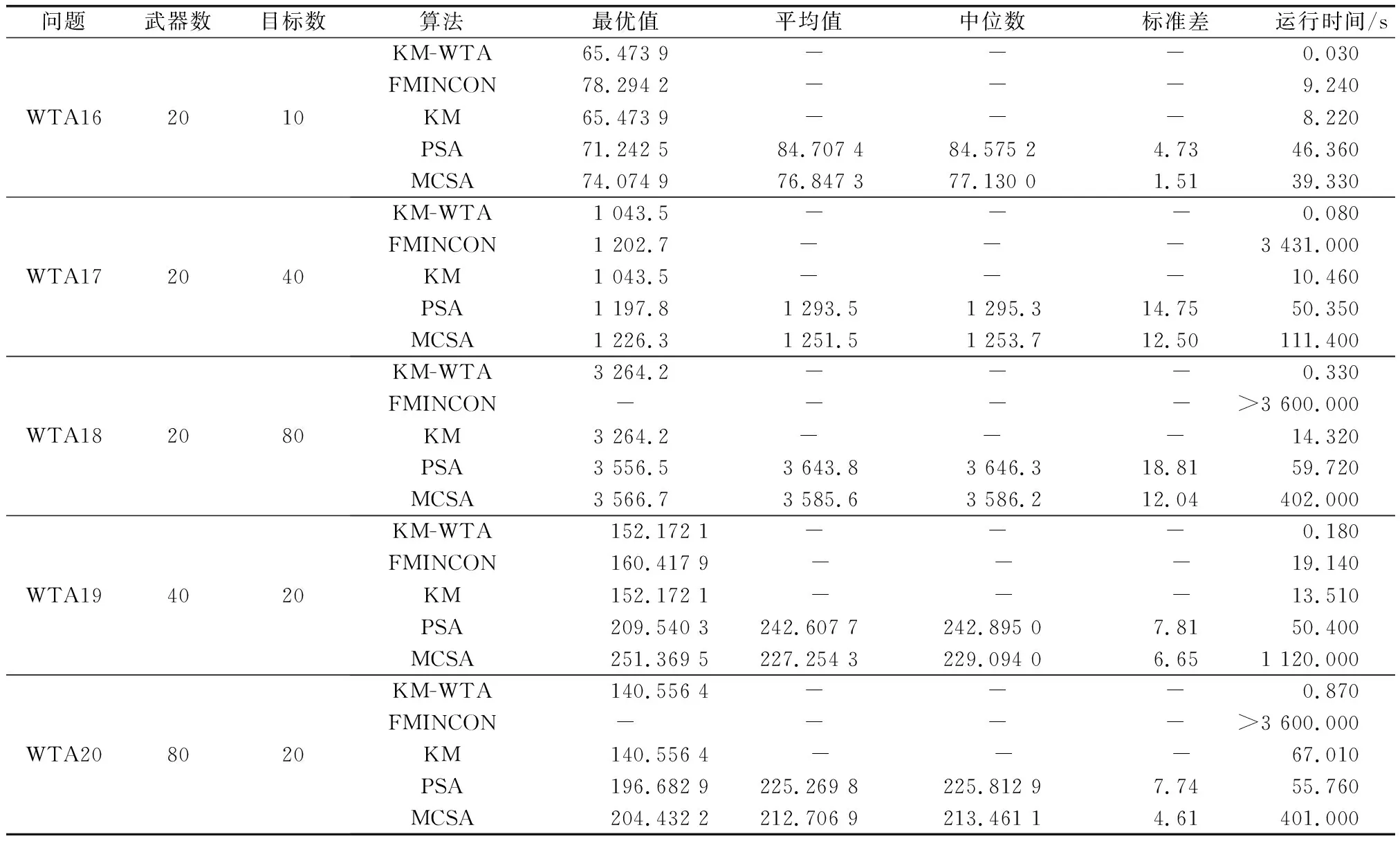
续表4

从表4可以看出,采用分支定界算法求解有约束的非线性规划式(9)～式(12)的难度更大,用时更长。在小、中规模的问题上求解精度也明显低于其他几种算法,在有限时间内很难找到大规模问题的最优解。

3.2.2 与KM算法对比

为了验证本文对KM算法改进的有效性,将KM-WTA算法与原KM算法在同一组实验数据上的运行结果和运行时间进行对比,计算结果如表4所示。

从表4计算结果可以看出,KM算法在问题规模达到70时计算时间已超过1 min,而改进KM-WTA算法在大规模问题上计算时间不超过0.5 min;在求解精度上,由于两种算法寻求最优解的原则思路相近,只是探索方式不同,因此运行结果基本相同。

两种算法的纵向对比可以说明,随着问题规模的增加,计算时间会变长,但KM-WTA算法的优势体现在其明显缩短了计算时间,能够快速求解规模较大的问题。

3.2.3 与PSA算法和MCSA算法对比

下面选取同样以WTA1～WTA12为数据集进行实验的两种近似算法与本文提出的方法进行实验对比,即PSA算法和MCSA算法。选择PSA算法的原因是该算法基于SA算法,是用于求解WTA问题的经典算法,PSA对SA的改进基于更优的算力,对本文所提算法的计算能力具有较好的参照性。选择MCSA算法的原因是该算法是典型的群体智能算法,也是目前元启发式算法中占比较大的算法种类,体现了种群进化过程中群体信息共享的作用,可以对本文所提算法的求解能力提供较好的对比。除此之外,这两种算法的实验模型与本文所研究的模型类似,尽量排除了模型不同对实验造成的影响。

同时,为了排除实验环境和编码语言不同对求解产生的影响,本文将PSA算法和MCSA算法在同一台计算机上进行复现,实验参数分别以相应参考文献中提供的参数为准,具体参数设置如表5所示。每个算法对每个问题计算10次后记录结果的最优值、平均值、中位数和标准差,每次计算的平均运行时间记录在表4中。

表5 两种算法的参数设置

在表5中,PSA[25]和MCSA[26]表示该行数据分别来源于文献[25]和文献[26],PSA和MCSA表示该行数据是与KM-WTA算法采用同一设备复现这两种近似算法的结果。但本文复现的结果与参考文献中提供的最优结果和运行时间数据都有较大差距。原因之一是实验环境与编程软件的差异,如文献[26]中PSA的实验环境为NVIDIA GeForce GTX Titan X(3072 cores, 1.0 GHz),MCSA的实验运行环境为Intel(R) Core(TM) i7-5600U CPU @ 2.60 GHz, with 8.00 GB of RAM,代码开发环境为CodeBlocks IDE v17.12;原因之二是随机算法求解效果受初始化、参数设置等因素影响较大,很难达到100%的复现效果。

因此,下面主要采用参考文献中提供的数据对结果进行分析,KM-WTA、PSA[25]和MCSA[26]在WTA1～WTA12问题上多次计算求得的平均值和标准差如图6所示。从标准差角度来看,KM-WTA是精确算法,每次计算结果都相同,其结果在图6中表示为一个红色圆点,标准差为0;而PSA算法和MCSA算法的结果只有在WTA1～WTA3上是一个点,在其他问题上都形成了长短不一的线段,说明多次计算存在标准差,求解结果不稳定。从平均值的角度来看,KM-WTA在WTA1～WTA5以及WTA9～WTA12上都得到了最优结果,平均值点都低于其他两种算法的平均值点或与其平均值点水平;在问题WTA6～WTA8中, KM-WTA的计算结果略差于PSA和MCSA,为了探究产生差距的原因,将式(7)和式(8)使用线性规划求解函数“intlinprog”进行计算,计算结果如表6所示,与KM-WTA算法得到的结果完全一致。由此可以断定,WTA6～WTA8计算结果较差的主要原因在于在简化模型过程中产生了误差,尽管KM-WTA算法是精确算法,但将非线性模型转化为线性模型时并非等价转换,导致未能找到原问题的最优解。

表6 WTA6～WTA8问题与intlinprog计算结果对比

图6 3种算法的计算结果对比Fig.6 Comparison of calculation results for three algorithms

同样地,将3种算法对12个问题的平均计算时间表示如图7所示。

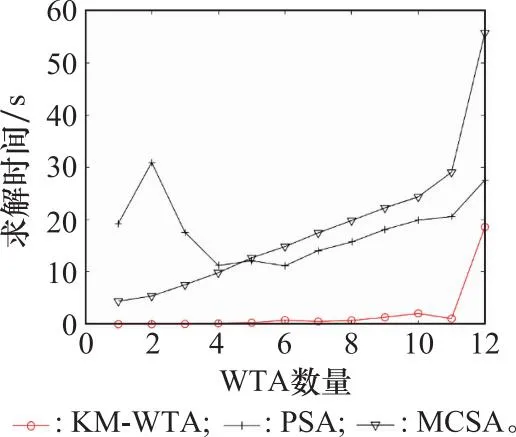
图7 3种算法的平均求解时间Fig.7 Average running time of three algorithms

从图7中可以看出,KM-WTA算法的计算时间远少于PSA算法和MCSA算法的用时,只有在大规模问题中,KM-WTA算法的运行时间才有明显增加,但依然低于其他两种算法。这也证明了KM-WTA算法计算复杂度低于近似算法,在求解速度上占有很大优势。

综上所述,本文提出的式(7)和式(8)是原问题模型式(9)～式(12) 的近似模型,需配合本文提出的KM-WTA算法求解,在20个实验问题中的17个问题上都取得了最优解,在未取得最优解的问题上仅比最优解差0.52%,并且比其他模型算法的计算耗时更短,说明本文提出的模型和算法在求解精度和求解速度上都具有一定的优越性。

4 结束语

本文首次将图论中的二分图匹配模型用于求解WTA问题,通过将WTA问题映射到加权二分图模型中,构建了一个新的数学模型,将非线性规划问题简化为线性规划问题,降低了模型的复杂度。为了进一步快速求解,在原始KM算法的基础上结合了贪心策略,极大地降低了计算的计算复杂度。通过在20个不同规模的问题实例上计算,分别对比了本文提出的模型与算法与初始的问题模型、KM算法以及两种启发式算法的计算结果和计算时间。实验数据说明,本文提出的模型与算法求解效率高,求解精度较高且求解速度快,同时多次实验也说明了该模型与算法计算结果稳定,适用于不同规模的问题。综上,本文提出的模型与算法可以满足实战中快速做出最优决策的要求,具有较强的实用性。

事实上,目前的研究重点逐渐转移到更加复杂的WTA模型。动态WTA问题需要考虑随着时间推移双方战力战况的变化,考虑多约束的WTA问题在离散解空间中添加更多武器或目标间的相互牵制关系,以及不确定的WTA模型需要在武器充足性不确定的情况下最大化总毁伤等各种复杂情况。研究的模型越复杂,研究结果对实际问题的指导价值也越高,如何用图论中的模型解决更加复杂的WTA问题,可以作为下一步研究的重点。