基于稀疏恢复的双基地机载雷达杂波抑制方法

王安安, 谢文冲, 王永良

(空军预警学院雷达兵器运用工程重点实验室, 湖北 武汉 430019)

0 引 言

双基地机载雷达由于收发分置,发射机和接收机的空间位置可灵活配置,甚至可依托无人平台抵近感兴趣的区域进行探测,相比单基地机载雷达具有更强的抗干扰、反隐身和战场生存能力,因而广受国内外研究者的关注。机载雷达的主要任务是探测空中目标,而其在下视工作时接收到的强地杂波会遮蔽目标信号,使得目标难以被发现,应用空时自适应处理[1-2](space-time adaptive processing, STAP)技术能够有效抑制杂波,提升信杂噪比(signal to clutter plus noise ratio, SCNR),有利于后续对目标的检测。

在STAP中,为获得良好的杂波抑制性能,必须准确估计杂波协方差矩阵(clutter covariance matrix, CCM)。双基地配置方式、收发天线放置方式和载机飞行方向等因素致使杂波的距离非平稳性增强,导致用训练样本估计的协方差矩阵与真实协方差矩阵相差较大,从而造成严重的性能损失。针对双基地机载雷达的杂波距离非平稳问题,学者们提出了自适应角度多普勒补偿法[3](adaptive angle-Doppler compensation, A2DC)、基于配准的补偿方法[4](registration-based compensation, RBC)和空时内插法[5](space-time interpolation technique, STINT)等,上述方法能够有效减少由杂波距离非平稳性带来的SCNR损失,但前提是杂波环境均匀。当面临非均匀杂波环境时,满足独立同分布的训练样本严重不足,杂波非平稳问题的STAP方法性能大幅下降。由于运动平台的杂波空时耦合特性,双基地机载雷达的真实杂波只分布在杂波脊附近,即在空时平面上具有稀疏性,这暗示了可通过稀疏恢复(sparse recovery, SR)方法来估计杂波在空时平面上的分布[6]。

SR-STAP方法能够在小样本条件下有效抑制杂波[6-15],因而有望解决双基地机载雷达杂波的非均匀和非平稳性导致的训练样本不足的问题。针对双基地机载雷达杂波抑制问题,文献[10]将多样本联合的稀疏贝叶斯方法用于重构CCM,进而进行STAP滤波,其性能较未经过杂波补偿的局域联合处理方法(joint domain localized, JDL)更好,但未考虑网格失配问题。SR-STAP方法通常将整个空时平面均匀划分,而双基地配置下的真实杂波脊往往不会落在网格均匀划分的网格点上,从而导致网格失配,严重影响SR-STAP方法的杂波抑制性能。针对网格失配问题,文献[11-12]利用贪婪算法的思想,在全局原子挑选准则的基础上增加了局域原子挑选准则,能够在一定程度上改善由网格失配带来的SCNR损失,但易受噪声的影响;文献[13]提出了基于最小原子范数的无网格稀疏恢复方法,此方法在单基地机载雷达的杂波脊斜率为1时的性能接近空时最优处理器,但在斜率不为1时性能明显下降;文献[14]提出了一种基于参数搜索的正交匹配追踪方法,此方法利用最速下降法来获取每个原子的失配量,但在模型中未考虑噪声信号;文献[15]提出的基于杂波脊先验信息的字典构造方法能够有效应对非正侧视阵的网格失配问题,但在构造字典时只考虑了杂波脊正面的信息,因此只适用于单基地机载雷达。

上述SR-STAP方法不能解决双基地机载雷达杂波存在的网格失配问题。在双基地机载雷达的背景下,本文针对网格失配问题在文献[15]的基础上提出了一种基于非均匀网格(nonuniform-grid based, NGB)的SR-STAP方法,仿真结果表明,NGB-SR-STAP方法的杂波抑制性能优于同类型使用均匀字典的SR-STAP方法。

1 双基地机载雷达杂波模型

假设发射机和接收机分别置于发射载机和接收载机上,其相控阵雷达天线均为正侧视均匀线阵,阵元数为N,阵元间距为d,雷达工作波长为λ,脉冲重复频率为fr,一个相干处理间隔(coherent processing interval, CPI)内的脉冲数为K。

以接收机为原点建立直角坐标系,如图1所示。图1中,T和R分别表示发射机和接收机,L0为基线长度;VT和VR分别为发射载机和接收载机的飞行速度;hT和hR分别为发射载机和接收载机的飞行高度;δT和δR分别为发射载机和接收载机飞行方向相对基线方向的方位角;RT和RR分别为发射机和接收机到杂波散射体P的距离;θT和θR分别为P相对发射机和接收机的方位角;φT和φR分别为P相对发射机和接收机的俯仰角。

图1 双基地机载雷达几何示意图Fig.1 Geometry schematic diagram of bistatic airborne radar

假设不存在距离模糊,则第l个距离单元的回波信号可表示为

x=xc+n

(1)

式中:xc表示杂波回波信号;n表示噪声信号,且有

(2)

(3)

(4)

第i个杂波块的空间频率和归一化多普勒频率可分别表示为

(5)

(6)

式中:RT,j、θT,j和φT,j均能以θR,i和RR,i为自变量进行表示[16]。

定义双基地距离和RS,i=RT,j+RR,i。图2给出了两种典型配置下的不同双基地距离和杂波空时轨迹,由图2可以看出:① 双基地机载雷达的杂波具有距离依赖性,即非平稳性,尤其体现在近程杂波上,但非平稳性随着双基地距离和的增大而逐渐减弱;② 双基地机载雷达的杂波分布受配置的影响大,在载机飞行方向共线时,类似于“形变”的单基地正侧视阵的杂波脊;在载机飞行方向垂直时,则表现为一个不规则的闭合曲线。

图2 双基地机载雷达杂波空时轨迹Fig.2 Clutter space-time trajectories of bistatic airborne radar

2 SR-STAP方法

(7)

(8)

由于式(7)只利用单个距离单元的数据,因此也称其为单观测矢量模型[17]。当利用多个距离单元的数据来估计杂波的空时分布时,式(7)可拓展为以下形式

(9)

式中:X=[x1,x2,…,xL]∈CNK×L表示L个距离单元的数据组成的空时采样信号矩阵;A=[α1,α2,…,αL]∈CNsNd×L表示L个距离单元数据中的杂波在空时平面上的幅度分布矩阵;N=[n1,n2,…,nL]表示噪声信号矩阵。式(9)也被称为多观测矢量模型。

在已知回波信号X的前提下,杂波空时分布A的问题可描述为

(10)

根据式(10)求解出A即可构造待检测单元的CCM,来计算用于杂波抑制的空时自适应权值。

3 NGB-SR-STAP方法

网格失配问题严重影响SR-STAP方法的性能,增大网格密度即减小网格间隔能够增加接近真实杂波脊的网格点,从而减轻由失配带来的性能损失,但无法解决网格失配问题。同时,不断增大网格密度并不会明显提升SR-STAP方法的性能,反而会带来计算量的增加[19]。导致网格失配的原因是划分的网格点偏离了真实的杂波脊,如果根据准确的杂波脊先验信息来划分网格,就能有效提升SR-STAP方法的性能。针对双基地机载雷达杂波的网格失配问题,本节将提出基于NGB的SR-STAP方法,以下记为NGB-SR-STAP方法。

由式(5)和式(6)可以得到待检测距离单元的杂波空时轨迹(其中载机的飞行速度和飞行方向可以通过导航系统或参数估计方法获得[20]),即归一化多普勒频率与空间频率之间的对应关系,本节用式(11)来表示,即

(11)

式中:G(·)表示以fs为自变量的单值或多值函数。

(12)

文献[15]只考虑了单基地机载雷达正面的杂波脊,即空间频率与归一化多普勒频率一一对应的情况,而在绝大多数双基地配置(除发射载机与接收载机飞行方向共线或发射机、接收机两者之一位于地面时的情况[21])的杂波脊上,单一空间频率往往同时对应两个归一化多普勒频率,本节以大多数情况下的杂波为例进行分析,即

(13)

(14)

(15)

且有

(16)

式中:i=1,2。

情况 1Δfd,i,n′>Δfs

(17)

情况 2Δfd,i,n′<ρΔfs

当|κi,n′|较大时,将相邻两个非常接近的归一化多普勒频率合并为一个,则第n′个和第n′+1个归一化多普勒频率集合可表示为

(18)

(19)

情况 3ρΔfs≤Δfd,i,n′≤Δfs

当|κi,n′|适中时,保持原有的间隔不变,则第n′个和第n′+1个归一化多普勒频率集合可表示为

(20)

(21)

(22)

(23)

(24)

(25)

需要注意的是,当发射载机与接收载机飞行方向共线或发射机、接收机两者之一静止时,初始归一化多普勒频率集合的组由2组变为1组,本节方法中的i=1,2退化为i=1,式(14)和式(15)需省去,其余步骤或处理流程均不变,因此NGB-SR-STAP方法适用于任意双基地配置情况。算法1给出了NGB-SR-STAP的伪代码。

算法 1 NGB-SR-STAP的伪代码(1) 初始化字典参数: f-s={f-s,1,f-s,2,…,f-s,n,…,f-s,Ns},f-d=⌀ f-d,i={f-d,i,1,f-d,i,2,…,f-d,i,n,…,f-d,i,Ns}=G(f-s) Δfs=1Ns-1,Δfd,i,n'=|f-d,i,n'+1-f-d,i,n'| n∈[1,Ns],n'∈[1,Ns-1], i=1 or i=1,2,ρ∈(0,1](2) 更新字典参数: for i=1 or i=1,2 for n'=1,2,…,Ns-1 case1 Δfd,i,n'>Δfs (f-d,i)n'={f-d,i,n',f-d,i,n',1,…,f-d,i,n',q,…,f-d,i,n',Q, f-d,i,n'+1} case2 Δfd,i,n'<ρΔfs (f-d,i)n'={f-d,i,n'},(f-d,i)n'+1={f-d,i,n'+2}

case3 ρΔfs≤Δfd,i,n'≤Δfs (f-d,i)n'={f-d,i,n'},(f-d,i)n'+1={f-d,i,n'+1} end f-d=f-d∪(f-d,i)n'∪(f-d,i)n'+1 end f-d,E={-0.5,…,f-d,min-Δfs,f-d,min}∪{f-d,max,f-d,max+ Δfs,…,0.5} f-d=f-d∪f-d,E,Nd=length(f-d)1)(3) 构造导向矢量字典: ～=[s(f-s,1,f-d,1),s(f-s,1,f-d,2),…,s(f-s,1,f-d,Nd),s(f-s,2, f-d,1),…,s(f-s,Ns,f-d,Nd)](4) 获得杂波空时分布: minAA2,0s.t.X-～A2F≤Lε(5) 计算权矢量: ^Rc=1L∑Lv=1∑NsNdu=1|α～u,v|2～u～Hu+λDLI, w=^R-1cssH^R-1cs

4 仿真分析

本节设计仿真实验来验证NGB-SR-STAP方法对双基地机载雷达杂波抑制的有效性。设置基线长度L0=50 km,载机飞行速度VT=VR=70 m/s,载机飞行高度hT=hR=3 km,双基地机载雷达采用3种配置,配置1为载机飞行方向共线的情况(δT=δR=0°),配置2为载机飞行方向垂直的情况(δT=90°,δR=0°),配置3为载机飞行方向平行的情况(δT=90°,δR=90°),雷达系统参数如表1所示。假设波束正确追赶,待检测单元位于双基地距离和为80 km处。在本节仿真参数下,杂波不存在距离模糊。

表1 雷达系统参数

实验 1不同尺度系数ρ的杂波谱估计性能

本实验分析尺度系数ρ对杂波谱估计性能的影响。图3给出了双基地配置2下的真实的杂波Capon谱,图4(a)～图4(c)给出了ρ=1、ρ=0.6和ρ=0.2时NGB-MSBL方法估计得到的杂波Capon谱。可以看出,当ρ较大时,估计出的杂波谱与真实杂波谱相差较大;随着ρ的不断减小,估计出的杂波谱更接近真实杂波谱,这表示估计出的CCM与真实的协方差矩阵之间的偏差逐渐减小。因此,通过设置合适的ρ可以保证在不过多增大计算量的同时更加准确地估计CCM,从而提升SR-STAP方法的性能。

图3 真实的杂波Capon谱Fig.3 Real clutter Capon spectrum

图4 不同尺度系数下NGB-MSBL方法估计的杂波Capon谱Fig.4 Clutter capon spectrum estimated by NGB-MSBL method with different scale coefficient

实验 2不同SR-STAP方法的杂波抑制性能

本实验对比NGB-SR-STAP方法和SR-STAP方法的杂波抑制性能。图5(a)～图5(c)分别给出了3种双基地配置下,NGB-SR-STAP、SR-STAP方法和空时最优处理器的SCNR损失,上述曲线均为100次蒙特卡罗仿真取平均值后的结果。由图5可以得到以下结论:① 所提方法在不同的双基地配置下对3种算法的性能均有不同程度的改善,在配置1情况下分别对MSBL-STAP、MFOCUSS-STAP和MOMP-STAP方法在主杂波附近的性能改善了约2.4 dB、3.2 dB和4.1 dB,在配置2情况下分别对以上3种方法在主杂波附近的性能改善了约4.3 dB、4.6 dB和4 dB,在配置3情况下分别对以上3种方法在主杂波附近的性能改善了约3.6 dB、2.1 dB和7.5 dB;② NGB-MSBL-STAP方法在3种配置下的性能均接近最优,NGB-MFOCUSS-STAP方法性能仅在配置1情况下接近最优,原因是在配置2和配置3情况下相关性强的导向矢量增加,在字典相关性较强时MSBL算法的稳健性要比MFOCUSS-STAP算法更好;NGB-MOMP-STAP方法在3种配置下的性能均较差,原因是MOMP算法的原子在搜索过程中易受噪声的影响。

图5 不同SR-STAP方法的SCNR损失Fig.5 SCNR loss of different SR-STAP methods

实验 3非理想情况下不同SR-STAP方法的杂波抑制性能

本实验分析NGB-SR-STAP方法在非理想条件下的稳健性。图6和图7分别给出了3种双基地配置下存在通道误差时和存在杂波内部运动[1]时NGB-SR-STAP方法、SR-STAP方法和空时最优处理器的SCNR损失,上述曲线均为100次蒙特卡罗仿真取平均值后的结果。通道间随机的幅相误差均为3%,杂波内部运动速度σv=0.1 m/s。对比图5和图6可以看出,存在通道误差时各方法性能下降明显,但NGB-SR-STAP方法在主杂波附近依然具有一定的改善功能;对比图5和图7可以看出,当存在杂波内部运动时,各方法性能略微下降,在配置1方式下NGB-SR-STAP方法对主杂波附近的SCNR损失改善了约2.6 dB、3.7 dB和5.8 dB;在配置2方式下NGB-SR-STAP方法对主杂波附近的SCNR损失改善了约2.8 dB、4 dB和4.4 dB;在配置3方式下NGB-SR-STAP方法对主杂波附近的SCNR损失改善了约0.7 dB、1 dB和6.2 dB。

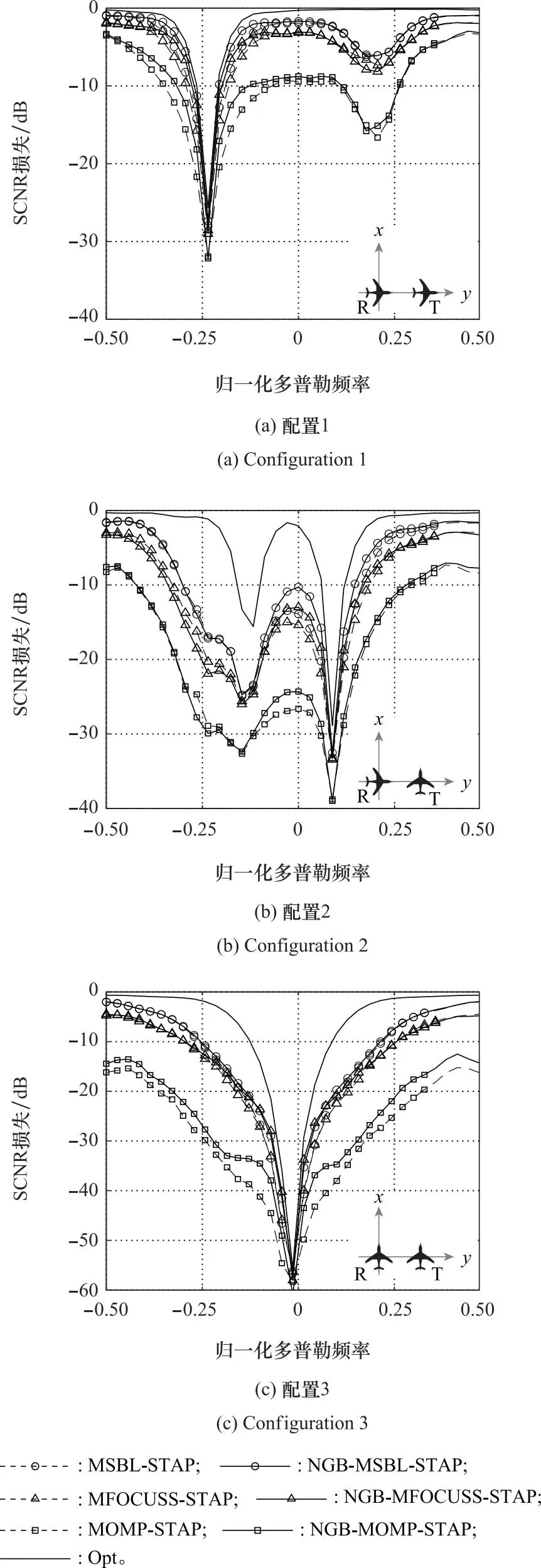
图6 存在通道误差时不同SR-STAP方法的SCNR损失Fig.6 SCNR loss of different SR-STAP methods in the presence of channel errors

图7 存在杂波内部运动时不同SR-STAP方法的SCNR损失Fig.7 SCNR loss of different SR-STAP methods in the presence of clutter internal motion

实验 4不同训练样本个数的杂波抑制性能

本实验对比NGB-SR-STAP方法与传统STAP方法在不同训练样本个数时的杂波抑制性能。图8给出了3种双基地配置方式下NGB-SR-STAP方法和经过RBC方法[4]补偿后的JDL方法的平均SCNR损失,平均SCNR损失定义为所有多普勒通道SCNR损失的均值,上述曲线均为40次蒙特卡罗仿真后取平均值的结果。JDL方法参与自适应处理的空域波束和多普勒通道数均为3,每个多普勒通道均增加60 dB的切比雪夫权。从图8可以看出:① 在相同配置下,随着训练样本个数的增加,各种方法的平均SCNR损失均得到了不同程度的降低;② 在配置1方式和相同训练样本个数情况下,3种NGB-SR-STAP方法的平均SCNR损失均优于补偿后的JDL方法;在配置2、3方式和相同训练样本个数情况下,NGB-MBL-STAP和NGB-MFOCUSS-STAP方法的平均SCNR损失均优于补偿后的JDL方法,补偿后的JDL方法在训练样本充足时的性能接近NGB-MFOCUSS-STAP方法;③ NGB-MBL-STAP和NGB-MFOCUSS-STAP方法对训练样本个数不敏感,即使在只有2个训练样本的情况下也能获得较小的平均SCNR损失。

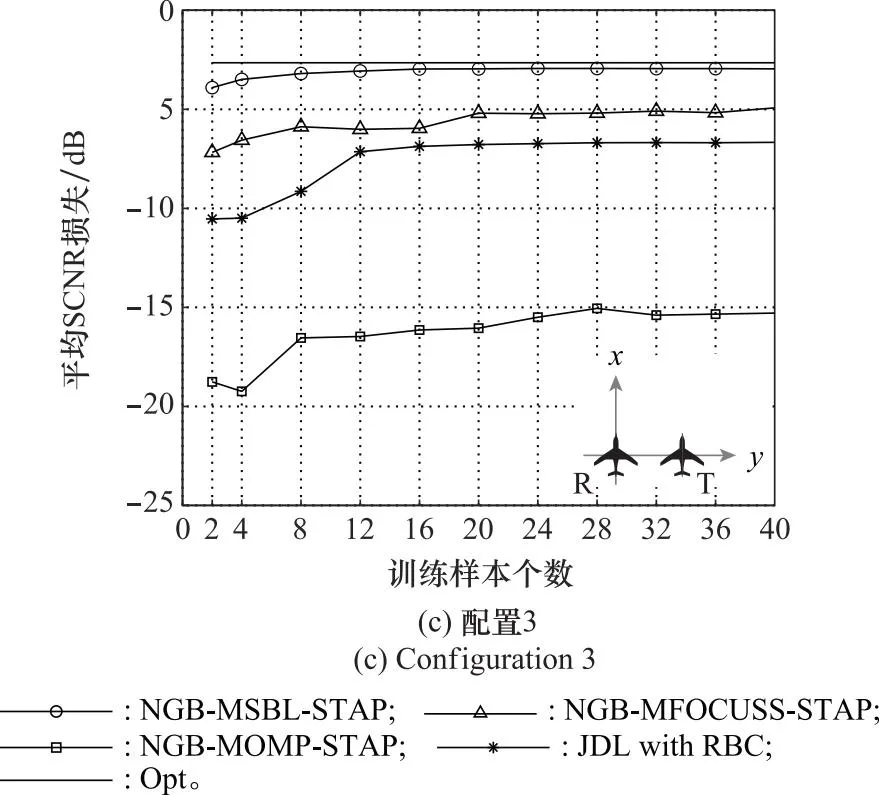
图8 不同训练样本个数的平均SCNR损失Fig.8 Average SCNR loss of different training samples

5 结束语

双基地机载雷达杂波存在的网格失配问题严重影响SR-STAP方法的性能。本文分析了双基地配置下导致网格失配的因素,将杂波脊先验信息用于构造非均匀网格,在此基础上提出了一种适用于任意双基地配置情况的基于非均匀网格的SR-STAP方法。仿真结果表明,本文方法的杂波抑制性能优于同类型使用均匀网格的SR-STAP方法,对训练样本个数要求更低,并在非理想条件下具有一定的稳健性。本文方法的缺点是仅适用于无距离模糊的情况,如何在双基地机载雷达背景的小样本条件下有效抑制距离模糊杂波将是下一步研究工作的重点。