基于低秩张量完备的电磁大数据标注补全算法

孙国敏, 张 伟,,*, 邵怀宗, 方 旖, 李鹏飞

(1. 电子科技大学信息与通信工程学院, 四川 成都 611731; 2. 电磁空间安全全国重点实验室, 四川 成都 610036; 3. 电磁空间认知与智能控制技术实验室, 北京 100083)

0 引 言

随着信息技术的飞速发展,数据逐渐成为继物质、能源之后的第三大国家基础战略资源和创新生产要素。大数据正深刻而广泛地影响、改变甚至重构人类社会。大数据也是支撑国家安全和军队建设的战略资源,大数据背景下的信息化战争将从根本上改变单一军种作战的思维定势,推动军事理论、体制编制、装备体系、战略战术、管理模式朝着与大数据背景下的信息化联合作战要求相适应的方向创新发展[1]。随着联合作战向陆、海、空、天、电、网等多维空间发展,电磁空间争夺日趋复杂。基于电磁空间多平台多类型侦察数据,利用智能化处理技术获取更高价值的情报数据信息,已经成为电磁空间作战领域的重要研究内容[2]。

对电磁大数据进行全面、准确地标注是后续进行智能化分析和处理的前提。目前,大多仍然依靠传统手工添加的方式对电磁数据进行标注分类。这种方式由于个人经验差异和有效信息不足,往往存在工作量大、错误繁琐、效率低下等问题。除此之外,还有基于启发式规则和模式匹配的标注方法,主要用于图像和文本数据的标注。基于启发式规则的标注方法,准确度不高且不具有通用性,不能对抽取到的全部数据添加语义注释[3]。模式匹配标注思想则利用预先建立的模式匹配关系,以互补的方式实现数据标注[4],但这种模式很难保证匹配关系的正确性。上述缺陷使得这两种方法难以适应强对抗非合作条件下侦察信息残缺、虚实难辨的电磁数据标注场景。针对战场对抗环境下多平台跨场景侦察数据存在的数据质量差、标注率低、标注信息缺失严重等问题,设计能够高效、准确地实现电磁数据自动化标注的算法就显得尤为急迫和重要。

本文结合电磁大数据低质量、多虚假、重冗余、无先验等特点,提出了一种基于低秩张量完备理论的电磁数据标注补全算法。低秩张量恢复可以看作是压缩感知的推广,即在原始矩阵(张量)低秩条件下,如何利用基于极稀疏块观测矩阵获得的观测数据恢复出原始张量[5-6]。目前低秩张量完备已经被广泛运用于图像修复、图构建和图像去噪等领域[7-10],但目前将其用于电磁数据标注信息补全的文献较少。本文从不同平台在一段时间内对同一目标的特征观测向量应高度相关这一基本事实出发,将多个连续时刻、多个平台对不同目标的特征观测(标注)向量构建为一个低秩张量,从而将缺失标注信息补全建模为低秩张量完备问题。考虑到这是一个复杂的非凸优化问题[11-13],本文设计了基于最大秩分解的迭代求解算法获得原问题的高质量次优解。分别利用实侦电子侦察数据和仿真数据对提出的标注补全模型的鲁棒性进行验证。结果表明所提方案和算法不仅具有良好的标注补全能力,还能够对错误的标注信息进行纠正,为电磁大数据的智能化处理提供有效的理论支撑。

1 标注补全问题建模

假设在某一特定的时间范围内,某作战区域内有m个监测平台,n个感兴趣的作战目标处于观测区域。对于每个感兴趣的目标,选取p个待侦察特征,包括目标的时间信息、方位信息(经度、纬度、海拔等)、速度信息、使用频段以及信号强度等,具体如表1所示。表1记录了各个平台在不同时刻ti(i=1,2,…,m)对不同目标的标注信息,“××”代表不同的标注数值。

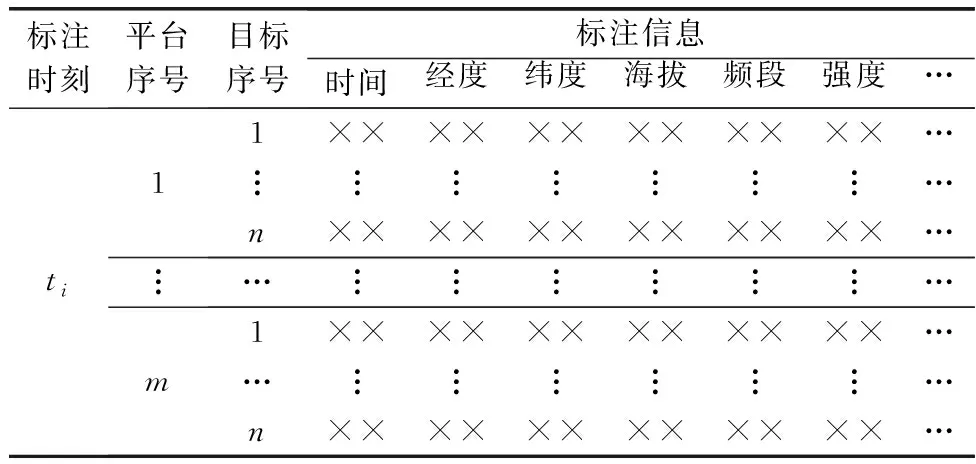
表1 电磁数据标注信息表

图1 电磁数据四维张量表征Fig.1 Four-dimensional tensor representation of electromagnetic data

由于非合作电子侦察的强对抗性,这些平台往往难以在所有时段都采集到目标的信息,再加上不同类型平台之间的异构特性,不同平台监测的特征参数(标注信息)也不完全相同,并且在同一时段,不同平台所处的“工作/维护”状态也不同。在表1或者X-4中,有大量信息是缺失的,如图3所示,其中白色的小方块代表对应位置的标注信息缺失。恢复张量X-4中缺失元素的过程就被称为标注补全,它是开展后续智能化分析和处理的前提和基础[14-15]。

图3 元素缺失的标注信息Fig.3 Annotation data with missing elements

基于前文所述,在一段时间内,不同平台对同一目标的某个特征参数观测所得结果应具有很强的相关性,且分段光滑。因此,X-3中属于同一目标的特征(标注)信息高度相关,故张量X-3的秩不超过目标个数N,即r=rank(X-3)≤N,即在有足够多的观测平台且测量的特征参数(标注项)足够多时,X-3是一个低秩张量,有r=rank(X-3)≪min{m,n,p}。此时,标注补全可以被看作为一个低秩张量恢复问题。根据压缩感知和张量恢复相关理论[16-17],低秩张量的每行或每列都可以用其他的行或列线性表出,所以矩阵中包含大量冗余信息。利用这些冗余信息,当矩阵的秩和已知元素数量满足一定条件时,可以大概率对缺失数据进行完美恢复[18-20]。因此,利用低秩矩阵恢复理论实现标注补全具有理论可行性[21-23]。

假设D-4为X-4的观测矩阵,包含X-4的已知标注信息。那么,基于低秩张量完备的标注补全问题可以建模为

(1)

式中:P表示投影算子,定义如下:

(2)

(3)

s.tPΩ(X-4)=D-4

(4)

由于计算n次核范数需要计算n次奇异值分解(singular value decomposition, SVD),计算代价很大,故可通过最大秩分解来降低计算量,具体如下:

s.t.PΩ(X-4)=D-4

(5)

这是一个凸优化问题[27-28],可以通过迭代邻近算子获得其局部最优解[29-30]。给定凸函数f(x),其邻近算子定义为

(6)

式中:ρ是正常数。最小化f(x)等价于

即可以通过迭代Proxf(xk)得到最优的x。

2 基于极大秩分解的标注补全算法

为了统一标注,本文有如下约定。mode-n展开的张量的定义为X∈RI1×I2×…×IN,张量X的第(i1,i2,…iN)元素可以表示为Xi1,i2,…,iN。两个张量X,Y的内积定义为

(7)

对应的Frobenius范数定义为

(8)

张量X沿mode-n展开的定义为X(n)∈RIn×∏i≠nIi,对应的逆变换记作X=foldn(X(n))。

考虑在一段时间内,不同平台对同一目标的特征参数观测所得结果应具有相关性,且分段光滑,依据两个光滑性先验约束,给出如下凸优化模型:

(9)

全变分正则主要用于度量像素与其周围像素的差异,差异越小,全变分正则越好。由于特征随时间变化具有分段连续光滑属性,故对Yn进行全变分正则能够有效描述这一属性。全变分正则TV(Yn)的定义为

(10)

下面给出求解式(9)中优化问题的算法。由模型易知,目标函数f(X-4,A,Y)对变量 (X-4,A,Y)非联合凸,对单个变量X-4,A,Y分别为凸。为了求解模型,这里引入邻近算子采用块坐标下降(block coordinate descent, BCD)方法。设T=T1×T2×RI1×…×IN,则Z=(X-4,A,Y)∈T,定义邻近算子

(11)

式中:α>0,为邻近变量;Zk=((X-4)k,Ak,Yk)。变量更新可以通过求解下面的问题来实现。首先,给出X-4更新子问题:

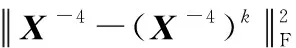
(12)

然后,给出A的更新子问题

(13)

最后,给出Y的更新子问题:

(14)

式中:

(15)

(16)

上述3个子问题可以分解为N个独立问题进行求解,具体见式(16),其中,Ωc表示已知标注指标集Ω的补集,且

(17)

针对Yn子问题,令

(18)

为了得到t(Yn)解的闭集形式,求解其等价形式:

(19)

式中:YT表示Y的转置矩阵。应用交替方向法(alternating direction method, ADM),上述问题可以转化为

(20)

式中:Ui,j=[(U1)i,j,(U2)i,j]∈R1×2,分别为U1,U2的第(i,j)个元素。Di的定义为

(21)

(22)

则对应的限制约束可写为

(23)

式中:Ii×i表示i×i的单位矩阵。对应的增广拉格朗日函数形式为

(24)

式中:Λ=(Λ1,Λ2)T为拉格朗日系数矩阵;σ>0为惩罚参数。通过交替方向优化方法进行更新有

(25)

对于Yn的子问题,有

(26)

该问题可以通过经典Sylvester矩阵方程进行求解,即

(27)

通过引入Kronecker乘积得到

(28)

(29)

式(29)可以写为

(30)

(31)

对于U-子问题,求解下面问题:

(32)

该问题可以通过求解下面的问题来实现

(33)

通过二维shrinkage方程求解,有

(34)

(35)

式中:[U1,U2]的计算复杂度为O(snrn)。在每一次迭代中,该算法所有的计算量为

(36)

最后,在算法1中对基于极大秩分解的标注补全优化算法进行小结。

算法 1 基于最大秩分解的标注补全算法1 令k=0, 初始化D-4, Ak, Yk2 repeat3 k=k+1;4 (X-4)k+1n=PΩc(∑Nn=1βnfoldn((Ak+1nYk+1n+α(X-4)k(n))/(1+α)))+D5 Ak+1n=((X-4)k(n)(Yk+1n)T+αAkn)(Yk+1n(Yk+1n)T+αI2)-16 vec(YTn)=(MnF*)(Σ2I+σIΦ2+αII)-1(M*nF)·vec(α(YT)kn+((X-4)T)knAkn-BTΛp-σBTCUp)7 until迭代过程收敛

3 实验与结果分析

算法评价指标包括峰值信噪比(peak signal-to-noise ratio, PSNR)和相对均方误差(relative squared error, RSE),分别定义为

(37)

(38)

式中:tol≤4×10-4。

为了充分利用张量数据不同维度间的相关性,下面分别在仿真数据和实测数据上对比二维、三维和四维数据的补全效果。

3.1 仿真数据测试

仿真数据测试是为了验证提出的补全算法在不同类型、不同维度数据下的鲁棒性。首先,介绍仿真数据的生成。第1步:生成大小为[32×24]的二维原始数据随机矩阵XX_2d_random,模拟单接收机某时刻24个不同目标32种特征的标注信息。第2步:利用二维随机矩阵XX_2d_random生成大小为 [32×24×16] 的三维张量XX_3d_random, 用于模拟跨接收机(16个接收机)在某时刻24个不同目标32种特征的标注信息。这里,XX_3d_random中,除第一个正向切片外,其余正向切片均由XX_3d_random引入随机噪声生成,即模拟同一时刻不同接收机的标注发生随机微小变化。第3步:利用三维随机矩阵XX_3d_random生成四维张量XX_4d_random,大小为 [32×24×16×42],用来模拟跨接收机在某一段时间内,即连续42个时间点24个不同目标32种特征的标注信息。除XX_4d_random(∶,∶,∶,1)=XX_3d_random 外,其余XX_4d_random(∶,∶,∶,j) 由XX_4d_random引入随机噪声生成,用于保持四维标注信息的低秩和光滑属性。对应的观测矩阵和张量通过随机抽取10%, 20%,…, 90%的数据置0来得到。下面在表2中展示原始矩阵XX_2d_random的部分数据。对应缺失率为30%的观测矩阵(前5列数据)在表3中给出。

表2 二维仿真数据原始矩阵

表3 二维仿真数据观测矩阵(缺失率为30%)

表4、表5和表6分别展示了二维、三维和四维观测矩阵在缺失率为30%的条件下,所提算法的部分补全结果(前5列数据),补全的标注用加粗字体注明。从标注数据的复原结果来看,所提算法能够有效复原缺失的标注。为了进一步分析算法的有效性,讨论所提算法在观测数据不同缺失率下的补全效果。表7和表8给出二维、三维和四维观测数据在缺失率为9种缺失率下的平均PSNR和RSE。

表4 所提算法二维仿真数据矩阵部分补全结果(缺失比例为30%)

表5 所提算法三维仿真矩阵部分补全结果(缺失比例为30%)

表6 所提算法四维仿真数据矩阵部分补全结果(缺失比例为30%)

表7给出了提出算法在不同维度观测数据、不同缺失率下标注补全结果的平均PSNR。从表7中可以看到,随着标注缺失率的不断升高,二维、三维和四维下补全结果的PSNR呈现下降趋势。这是由于缺失的标注越多,观测数据的质量越差,越难进行标注补全。对比二维、三维和四维标注数据在同一缺失率下的复原结果,易得提出的算法在四维张量的补全结果的PSNR高于三维张量,三维张量补全结果的PSNR高于二维矩阵。这表明提出的补全算法能够充分利用高维数据数据信息中隐藏的低秩、光滑属性,从而改善标注补全效果。

表7 所提算法仿真数据不同缺失率下的PSNR

表8展示了所提算法在不同维度观测数据、不同缺失率下标注补全结果的平均RSE。与PSNR相反,随着标注缺失率的不断升高,二维、三维和四维下补全结果的RSE随之增长。这是由于缺失的标注越多,观测数据的质量越差,标注补全的误差越大。对比二维、三维和四维标注数据在同一缺失率下的复原结果,易知所提算法在四维张量的补全结果RSE低于三维张量,三维张量的补全结果RSE低于二维张量,这表明基于高维数据的低秩、光滑先验,所提算法的补全结果误差更低,复原效果更好。

表8 仿真数据在不同缺失率下的RSE

3.2 实测数据测试

使用雷达模拟器搭建如下测试场景:利用20个电子侦察监测平台,对区域中100个雷达目标进行持续跟踪监测,监测时长为100 s,监测数据为归一化的雷达脉冲描述字(pulse description word, PDW),包括5种参数,分别为脉冲载频(radio frequency, RF)、脉冲宽度(pulse width, PW)、幅度(amplitude, AM)、到达角度(angle of arrival, AOA)和脉冲重复频率(pulse repetition frequency, PRI),分别构建大小为[100×5]的二维标注矩阵XX_2D,用于表征区域中100个雷达目标的5种PDW参数、构建大小为[100×5×20]的三维标注矩阵XX_3D,用于表征区域中100个雷达目标在20个电子侦察监测平台的5种PDW参数、构建大小为[100×5×20×100]的四维标注矩阵XX_4D,用于表征区域中100个雷达目标在20个电子侦察监测平台监测时长为100 s的5种PDW参数。XX_3D将不同监测平台数据进行整合,生成三维张量,充分利用不同平台间侦测数据的相关性,即低秩先验;XX_4D进一步将不同时刻的侦测数据进行整合,生成四维张量,充分利用不同平台连续时间内数据的低秩和光滑先验信息。

下面分析所提算法在实测数据上的标注补全性能。测试分为两部分:标注补全和标注纠错。其中,标注补全包括二维、三维和四维标注数据在不同缺失率下PSNR和RSE的对比分析。

3.2.1 标注补全

首先,在表9和表10中分别展示二维原始标注数据、30%缺失率的部分标注数据。

表11、表12和表13分别展示了二维、三维和四维标注数据在缺失率为30%时所提算法的部分补全结果(补全的标注用加粗数据注明)。从标注补全的数据来看,所提算法能够有效复原缺失的标注。为了进一步分析算法的有效性,讨论所提算法在真实观测数据不同缺失率下的补全效果。

表9 二维实测数据原始矩阵

表10 二维实测数据观测矩阵(缺失率为30%)

表12 所提算法三维实测数据部分补全结果(缺失比例为30%)

表13 所提算法四维实测数据部分补全结果(缺失比例为30%)

表14和表15分别给出二维、三维和四维观测数据在9种不同缺失率下的平均PSNR和RSE。

表14 所提算法实测数据不同缺失率下的PSNR

表15 所提算法实测数据不同缺失率下的RSE

表14给出了二维、三维和四维真实观测数据在不同缺失率下,所提算法标注补全结果的平均PSNR。由表14易知,随着缺失率的升高,3类数据补全结果的PSNR不断下降,主要原因是标注缺失越多,观测数据的质量越差,算法越难进行标注补全。对比二维、三维和四维标注数据在不同缺失率下的补全效果结果,易知所提算法在缺失率较低时,二维和四维标注数据的补全结果的PSNR差别不大,三维标注数据表现较差。在缺失率较高时,四维张量补全结果的PSNR高于三维张量,三维张量补全结果的PSNR高于二维张量。这表明所提补全算法能够充分利用不同平台在一段时间内对相同目标的特征高维数据信息中隐藏的低秩、光滑属性,改善标注补全效果。

表15给出了二维、三维和四维真实观测数据在不同缺失率下所提算法标注补全结果的平均RSE。与PSNR相反,随着缺失率的升高,二维、三维和四维数据补全结果的RSE呈增长趋势。由于缺失的标注越多,真实雷达标注观测数据的质量越差,标注补全的误差越大。对比不同维度标注数据在不同缺失率下的RSE,易知在缺失率较高时,所提算法在四维张量的补全结果RSE低于三维张量,三维张量的补全结果RSE低于二维张量,这表明充分利用高维数据的低秩、光滑先验,能够降低补全误差,改善复原效果。

3.2.2 标注纠错

对于标注纠错,首先,在数据预处理时,对明显的标注错误进行缺失处理,即将错误标注置0;然后,进行缺失补全。下面展示所提算法在实测数据上的纠错效果。表9中加粗的数据为两处明显的标注错误,表11、表12和表13分别给出了二维、三维和四维数据下所提算法的纠错效果,三者具有类似的补全效果。

可以看到,对于明显的错误标注信息,所提算法能够有效纠错,这是由于所提算法充分利用二维、三维和四维张量数据的低秩和光滑先验信息,从而提高了算法的标注、纠错能力。

4 结 论

在大数据时代,标注良好的数据是进行各种智能处理和分析的前提。但是,在战场等特殊环境下,多平台、多类型电子侦察数据存在的标注率低、标注信息缺失严重等问题,为电磁大数据智能处理带来了困难。本文针对该问题,提出基于低秩矩阵恢复的电磁大数据标注补全解决方案。该方案基于不同平台对相同目标的特征参数测量结果应大致相同这一基本事实,将标注补全问题抽象为低秩矩阵恢复问题,然后设计了两种基于极大秩分解的标注补全算法。仿真结果表明,在元素缺失50%的极端情况下,所提算法仍可有效实现矩阵恢复与数据标注,同时该方法还具有一定的标注纠错功能。