邹伯奇关于日影观测“椭圆影心非日心”的数学解读
2024-01-29廖运章李杰民
廖运章 李杰民
(1.广州大学 数学与信息科学学院,广州 510006;2.岭南师范学院 数学与统计学院,湛江 524048)
圭表测影历史悠久,为使测量更精确,古人不断改进圭表测影技术和方法。元代郭守敬(1231—1316)用装有景符的四丈高表测量日影,改测表端投影为测横梁投影,将“仅如米许”的太阳像中心视为日面中心[1]。《崇祯历书·交食历指》(1632)认为,太阳透过小孔斜射到密室地面的投影,“所得形必长圆(即椭圆)”[2]。此后,天文学家大都认为椭圆光影之中心即太阳中心的投影。其实,在清道光二十四年(1844)前后,岭南科学家邹伯奇(1819—1869)就已发现“椭圆影心非日心”这一郭守敬及后人没有意识到的问题[3],并从数学上予以解读。因邹伯奇没有正式发表该论述(只有手稿存家,内容收入其遗著《测量备要》)[4],近现代天文史家对此并不知悉。事实上,邹伯奇关于日影观测“椭圆影心非日心”的论述,建立了“椭圆影心非日心”的数学模型,是对郭守敬圭表测影理论的完善,为日影测量之误差分析等提供了新判据,对圭表测影研究具有重要意义。
1 日心观测及其发展
1.1 元明清的日心观测
元代开始使用圭表顶端横梁测影,太阳光通过景符微孔在圭面上形成米粒大小的太阳像,横梁平分日像时可测得日心影值。《元史·历志·授时历议上》描述,“旧法以表端测晷,所得者日体上边之景,今以横梁取之,实得中景,不容有毫末之差”[5]。
《崇祯历书·交食历指》卷7“以长圆形求日食方法”节,称“正对太阳,其景(影)必圆。今以斜对之平面,亦在密室中受景(影),孔仍小如前,则所得形必长圆”。此处“长圆”即椭圆,椭圆知识明末清初始传入我国。([2],10-11页)
《历象考成》(1722)中载有太阳视径观测法,称“中表系横梁,上下皆空,太阳上边之光射横梁之下面,太阳下边之光射横梁之上面,其所生之影必当太阳之中心”;“太阳上边之光从孔南界射入,至案为椭圆形之前界,与正表之理同。太阳下边之光从孔北界射入,至案为椭圆形之后界,与倒表之理同,故两高度之较即为太阳之径也”。[6]
欧洲也有晷影观测的传统,或在教堂,或在天文台。“西洋人每观测日影,向南立高墙数丈,凿孔以通日影于地,铺一铜板于平地,分为万分之数观之,则见之甚易。比较铜板之日光照在何宫,则较目视日晷,极其清晰。”[7]“18至19世纪法国也注意日晷改良。它不重视日景的长短,常在屋宇墙壁穿孔以通日光,求取太阳高度。度量日景长短,则以孔的中心为起点。这类日晷多设在教堂内……”。[8]
《钦定大清会典》史部卷86记载:“史云何承天始立表候日影,前明观象台下设晷影堂,南北平置铜圭于石台上……南端植铜表高八尺,上设横梁用影符以取中影。本朝加二尺,表高一丈,上端安铜片,中开圆孔径二分。午正太阳之影自圆孔射至圭面成椭圆形,南界为日体上边影,北界为日体下边影,中心为中影。”[9]
邹伯奇认为,“国朝晷影堂之法,则于表端置铜片,开小孔,使漏光于圭面,成椭圆形,北为日下边影,南为日上边影。伯奇尝仿此二术,精心测量窥几之下,现出小圆光亦为椭形面,而圆心非即日心”;“谨按以椭圆影揆日高度。国朝测候度越前古之一端也,而会典载以中心为中影云云,殊欠分明,故撰此图说明之。又按此不过设数以明椭圆影心非日心,其实日近地平,其上下边及日中心之清蒙气差多少不同,故视日纵横径亦微异,虽以仪器折中取日心,亦非真视度也”。[10]
直至晚清,除了邹伯奇,人们一直认为,太阳透过小孔斜射到地面的投影为椭圆、投影椭圆的中心即日心——“椭圆影心即日心”,以致近现代天文史家亦没有意识到邹伯奇“椭圆影心非日心”的论断,仍沿用《大清会典》的观点。如陈遵妫按照郭守敬和清代天文学家的思路,认为“正午时候,太阳影子经过圆孔射到圭面成椭圆形状;南界是日面上边缘的影子,北面是它的下边缘的影子,中央是日面中心的影子”([8],1275页)。
1.2 日心观测的现代模拟
现当代,有学者对郭守敬圭表测影进行数据分析或模拟测量[11],因邹伯奇“椭圆影心非日心”不为世人所知,相关诸多研究文献依旧沿袭“椭圆影心即日心”的“郭法”(1)为行文简洁,本文称《元史·历志》郭守敬圭表测影改进之前的方法为“旧法”,郭守敬的方法为“郭法”,邹伯奇的方法为“邹法”。严格地说,“邹法”并非具体方法,只是“郭法”理论上的完善。来计算影长,这样计算的影长存在系统误差(2)正态分布是数学家高斯研究误差时发现的,正态分布又称为误差分布,测量误差近似服从正态分布,系统误差不服从正态分布。通常情况下,若无系统误差和人为过失误差,测量值与真实值的比较,偏大偏小的数据占比均应接近50%。,但几乎没有引起研究者注意,仅从测量误差或测量的客观条件不佳等角度去归因,导致对误差产生的原因界定不清。
比如,肖尧、孙小淳用北京古观象台的圭表进行模拟测量,得到29组影长数据[12];崔石竹、李东生同样用北京古观象台的圭表进行仿古测量,得到181组影长数据[13]。理论值大于或等于测量值的,前者有9组(31.0 %)、后者有124组(68.5 %);理论值小于测量值的,前者有20组(69.0 %)、后者有57组(31.5 %)。如果没有系统误差和人为过失误差,而且理论值计算正确,则测量值与理论值的比较,偏大偏小的数据占比应该均接近五成,然而上述两组研究者的测量数据分布均不符合预期。
王玉民认为,“冬至圭表测影是一种倒退的技术”,“即使采用景符,测量冬至影长的误差仍远远高于测夏至时的误差”,将测量误差归因于“冬至投射角太低造成的弥散度问题”等客观因素。[14]其实,邹伯奇“椭圆影心非日心”能清晰地说明,存在系统误差才是内因。
2 邹伯奇“椭圆影心非日心”的数学解读
邹伯奇,号特夫、特生,又号征君,广东南海人,是清末百科全书式学者[15],我国近代科学先驱[16],在数学、物理学(力学、光学)、天文学、测绘学和仪器制造等方面造诣精深,生前未能刊行论著,留下大量科学手稿。
2.1 “椭圆影心非日心”史料的发现
同治十三年(1874),亲友选出部分手稿刊刻《邹征君遗书》,“复有未定之书、《测量备要》二册”等由后人保存。([3],222页)1954年,邹伯奇曾孙邹孟才将“另手抄邹氏遗稿贰本”捐献给广州博物馆,并用竖行印有“广州市文一教育用品有限公司印售(纸12)”绿格“稿纸(20×20)”抄辑,送交邹伯奇后裔保存至今。1962年,邹孟才将“最近捡得的手稿一部分”散稿和实物赠给梁恒心,2009年,邹伯奇后裔整理保存和搜集到的遗稿,出版《邹伯奇遗稿》一书,其中披露了从未面世的“椭圆影心非日心”的具体内容。2011年起笔者先后数次到邹伯奇故居访问,邹伯奇玄孙邹忠廉赠与笔者他保存的《测量备要》等4本抄辑本之复印件,为邹伯奇遗稿的转抄本。“椭圆影心非日心”具体内容,包括“[圆锥斜剖成椭圆面],圆窖斜截成椭圆算草并图”,收录于《测量备要》辑本A和无书名但页码连续的B1本(页码由三至七三),内容相同,抄写笔迹不同。每叶左上格外均有“NO.”英文字母,用于编页码,每页的右叶用汉字数字编码,如NO.三十一、NO.三十二等。([4],90-92页)
事实上,邹伯奇关于“椭圆影心非日心”的论断,早有提及。陈澧《东塾集》卷3“邹特夫《学计一得》序”称:
又尝在余斋中论测日旧法未密,日光穿表端之孔而下为圆锥形,斜射平版而成椭圆,椭圆心非圆锥心,即非日心,乃创椭圆求圆锥心法。时梁南溟、侯子琴、徐子远同在座,三君与余皆疑圆锥斜截之面,两端不等,非真椭圆也。余遂设数以算之,两端正相等,乃叹此法为中西天算诸书所未及也。[17]
《邹征君遗书》拾芥园刻本记载:
《学计一得》者,吾友南海邹君特夫所作也。……特夫又尝过余,斋中论测日法未密,日光穿表端之孔而下为圆锥形,斜射平版而成椭圆,乃立法以椭圆面求圆锥心为日心。是时梁南溟、侯子琴、徐子远皆在座,余皆疑圆锥斜截之面,两端不等,不得为椭圆,三君以为然。余乃设数(以)算之,两端竟相等,乃皆叹服此法为中西天算诸书所未及也。……旧事历历在目,而俯仰之间,不觉十余年矣。……特夫昔以此编属余为序。余爱其精识神解,读之不倦,顾连年夷乱,屡欲为序,逡巡不成,不觉又三年矣。……咸丰八年九月陈澧书于横沙之崇雅楼。
陈澧谈及“椭圆影心非日心”这两段话,内容稍有出入,但均认为:一是“日光穿表端之孔而下为圆锥形,斜射平版而成椭圆”;二是“椭圆心非日心”。这正是邹伯奇“椭圆影心非日心”的两个核心观点。
梁恒心在《邹伯奇摄影史料初探》(1963)中抄录了一段邹孟才赠与的散稿原文,并分析认为这是发明“摄影之器”的证据和理论基础:
孔若小则光道系圆锥体,以孔为其顶点,以纸从直角遮断其光道,则其被照部分作圆形,纸距孔益远,则圆形亦大焉。又若以纸从横遮其光,或使光射于地上,则被照部分乃成椭圆形而非圆形矣。旭日初升,而见树木之影倒影于寝室之壁者,以日光自户隙而入故也。[18]
梁恒心又从陈澧作序的时间(咸丰八年,1858)推测,“从陈澧作序上推十余年,约在道光廿余年,这和摄影之器制成的时间(道光甲辰年,1844)相近,他的理论根据,从这里可以看到,而送来的手抄稿亦可以断定确定为邹伯奇原作。”
综合陈澧“邹特夫《学计一得》序”、邹达泉有关“《测量备要》二册”识记、广州博物馆“另手抄邹氏遗稿贰本”接收遗物清单、梁恒心抄录的散稿原文、《测量备要》抄辑本等史料,我们认为,梁恒心的推测较为合理,故推知邹伯奇发现“椭圆心非日心”的时间约在1844年前后。
邹伯奇遗稿转抄本中的“椭圆影心非日心”史料,存在错漏,特别是数字、图标等缺失,在不影响原意的情形下,经反复推算后予以合理修正。
对于“椭圆影心非日心”问题,邹伯奇首先论证“轴线不过椭圆心定理”,继而以之建构“椭圆影心非日心模型”,从而订正前人“椭圆影心为日心”之误。
2.2 “椭圆影心非日心”数学模型
邹伯奇首先在《测量备要》遗稿转抄本B1本(“NO.三一”页,图1)中,概要式地描述平面斜截圆锥的“轴线不过椭圆心定理”、“椭圆影心非日心模型”及其历史渊源和存在问题,主旨是“圆锥斜剖成椭圆面,其椭圆中心非锥心,必谆谆致辨者,为测影故也”。
图1 遗稿转抄本“三一”页
邹伯奇在简述郭守敬圭表测影方法和“国朝晷影堂之法”等的基础上,依这两种测影之术,开展实地观测,“精心测量”发现“椭圆心非即日心”,有悖传统结论,于是,给出原因:“盖圆柱斜[剖]成椭圆,柱心即圆心。若圆锥斜剖成椭圆,则心必偏于一端。试取竹笋斜剖之,视即明矣。”即借助圆柱斜截成椭圆轴线过椭圆心、圆锥斜截成椭圆而椭圆心偏移的数学结论,建构“椭圆影心非日心”的数学模型。
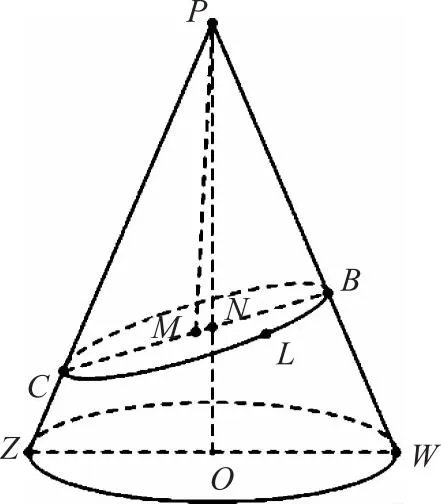
图2 椭圆影心非日心图
事实上,“轴线不过椭圆心”定理的天文意义,就是“日光从小孔交射而下,即为圆锥形,现于圭面,即斜剖之迹也(椭圆)。此理一经道破,莫不顿悟,而或疑其非正椭圆,则未经实测故也”。“椭圆中心非锥心”(不妨称邹伯奇椭圆影心非日心模型),用现代数学语言描述为:
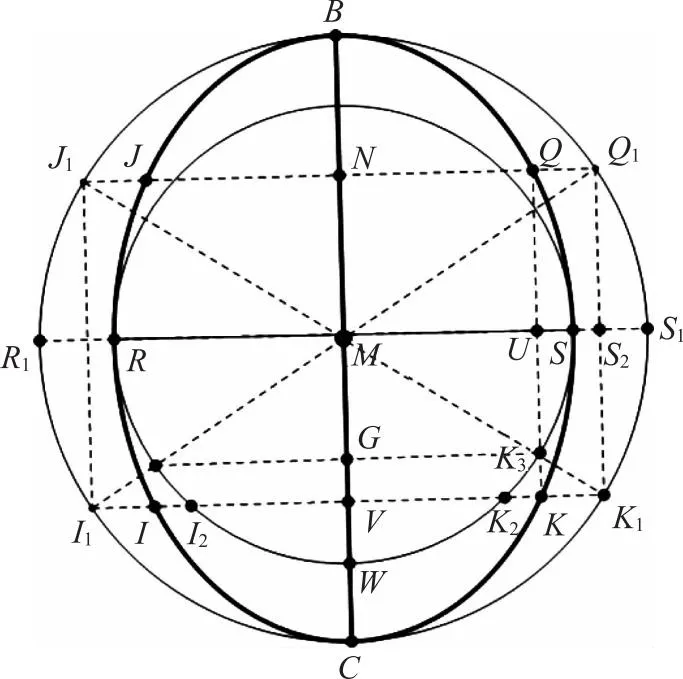
[轴线不过椭圆心定理]如图2,在圆锥PZW中,沿不平行于圆锥底面的平面斜截圆锥,所得截口BLC是椭圆,且PM与圆锥的轴线PO不共线(M是椭圆中心、O是圆锥底面圆心)。
[椭圆影心非日心模型]如图2,太阳光穿过天文仪器景符的小孔P后形成阳光圆锥PZW,阳光圆锥PZW在地面上的投影是椭圆BLC,太阳中心的投影点为PO与椭圆BLC长轴BC的交点N,而不是椭圆影心M。
对于轴线不过椭圆心定理,邹伯奇用斜截竹笋的实例进行直观诠释,其中蕴含着椭圆的两种形成方法(“圆柱斜[剖]成椭圆”、“圆锥斜剖成椭圆”),反映出邹伯奇对椭圆知识的掌握情况。明末清初,西方椭圆知识逐渐传入我国,利玛窦最早带来椭圆知识,罗雅谷与汤若望《测量全义》(1631)、邓玉函《测天约说》(1633)分别给出椭圆形成方法——斜割圆柱、截圆锥法,南怀仁《灵台仪象志》(1674)传入椭圆的拉线画法;《测量全义》传入椭圆面积的阿基米德求法,张诚和白晋翻译巴蒂的著作《几何原本》,又给出一种新的求椭圆面积的方法——比例法[19];《交食历指》、《历象考成后编》(1742)先后传入椭圆基本定理等([8],39-42页)。相继传入的椭圆第一定义、椭圆基本定理、面积公式等知识,受到中算家的重视与研究,邹伯奇是熟知这些知识的。
值得注意的是,阳光通过景符小孔在圭面上形成椭圆影已是常识,但该椭圆影是否为“正椭圆”则存有疑问,邹伯奇认为“未经实测”,于是“今设算草并为图以明之”,即下述“圆窖斜截成椭圆算草并图”。
2.3 例证轴线不过椭圆心定理
邹伯奇借助一个具体几何模型“圆窖”(圆台),以“圆窖斜截成椭圆算草并图”(图3)为题([10],32-34页),论证“圆窖者,即圆锥之下体也,圆窖斜截面既成正椭圆,则圆锥亦然”,得出结论“圆窖之中线与椭圆面长径线交于辰,非长径之一半,故知圭面椭圆影长径之半非日心所射也,再设数核之”。

图3 遗稿转抄本“三二”页
该圆窖的具体数据是:“设如有圆窖,上径六尺四寸(甲乙),下径十尺(寅丑),高五尺七寸二分三厘六毫三丝五忽,从上右(甲)斜剖至下左(丑),成椭圆面。”
邹伯奇例证(具有一般性)的思路是“圆锥斜截面是正椭圆,椭圆心非日心(投影)”。如图2,先论证椭圆BLC为正椭圆,再证明N与M不重合,从而PM与PO不共线。
设图3遗稿转抄本中天干地支图标对应的字母依次为:A乙、B甲、C丑、D寅、E辛、F己、G卯、J未、K子、L壬、M庚、N(图3辰出现两次,标记有误,这里N对应图3右上方的辰,左下方的辰对应S)、Q申、R午、U丁、V癸、X丙、Y戊;原文无标注的,为行文方便,加标字母I、O1、O2、O3、P等,如图4—6。
由图4,设圆台ABCD的上底直径AB=6.4、下底直径CD=10、高BG=5.723635。(3)原文此处单位为尺,长度单位有丈、尺、寸、分、厘、毫、丝、忽等,为十进制,所以直接用数字表示,省略单位,对推理与结论均无影响。BC是斜截面椭圆的长轴,知GD=1.8,CG=8.2,在RtΔBGC中,由勾股定理得BC=10。EF是圆台中截面的直径,与BC交于M,知MF=CD/2=5,EM=AB/2=3.2,由勾股比例(射影定理)MF·EM=MS2(图6),故椭圆半短轴b=MS=4。同理,可求VQ=3.2=UJ(图5)。
另由图5,椭圆内含两个面积相等的RtΔUVQ、RtΔUVJ以及等腰RtΔUVS,其中垂线MS=b=4,由椭圆定义(到两个焦点的距离之和为2a)得US+VS=2a=10,同理UQ+VQ=10;在RtΔUVQ中,UV=2c=6,由勾股定理UQ2=VQ2+62,解方程组亦可得VQ=3.2。
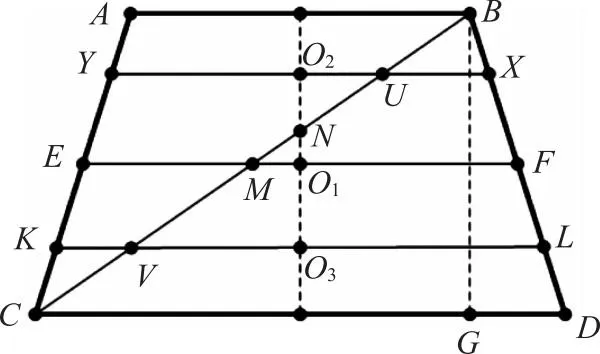
图4 圆台纵截面图

图5 圆台斜截面图(椭圆)
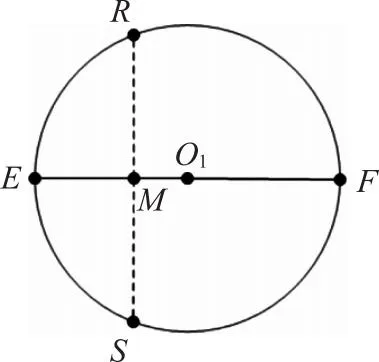
图6 中间横截圆面
简而言之,若知圆台的高与上下底面直径,可求斜截面椭圆的长径;作圆台的中截面,可求斜截面椭圆的短半径;作与圆台中截面对称的两个横截面或用椭圆定义与勾股定理,可求得椭圆的其他弦长,且对称的弦长相等。于是,斜截面椭圆是“正椭圆”。
因圆台是圆锥的一部分,圆台的斜截面是椭圆,则圆锥的斜截面也是椭圆,圆台的中轴线与椭圆面的长轴交点为N,由图4可知,2BN≠BC,即N不是BC的中点,从而N与M不重合,PM与PO不共线。故由图2,圭面上投影椭圆的中心M并非日影点N。
邹伯奇没有定义“正椭圆”,可能是一种通俗说法,从上下文看,指“过两焦点并垂直于轴的弦长相等”之椭圆,就是常规的标准椭圆(关于主轴对称),以此回应陈澧等“圆锥斜截之面,两端不等,不得为椭圆”的疑虑。
2.4 椭圆影心非日心模型的观测实例
椭圆影心非日心模型(邹法),实质是轴线不过椭圆心定理在日影测量上的应用。郭法测日影,将椭圆中心M视为日影点,而邹法证实日影点是N,郭法测日影存在系统误差NM。

图7 遗稿“三五”、“三六”两页拼接(4)图7中太阳示意图没有标字母,遗稿“三八”页后另附一页,为另一人笔迹,文字内容相同,但太阳示意图标有字母,将其拼接到图7中。
邹伯奇的论证,基于一个具体日心观测实例(图7),原文与“圆窖斜截成椭圆算草并图”一一对应,沿袭轴线不过椭圆心定理的证法,推理步骤几乎一致,因已知条件不同,推理略有差异:
设如日距地平一度四十五分,日半径十五分,西边有墙(如丙甲),掩之墙东一平地(如甲乙),距平地上一丈(如丁甲),有小孔漏日光(丁)射于平地上,成椭圆形(如辛己庚戊)。西边(戊),日上边(乾)所射,距墙(戊甲)二十八丈六尺三寸六分二厘四毫九丝八忽,二度之余切也;东边(己),日下边(坤)所射,距墙(己甲)三十八丈一尺八寸八分五厘二毫八丝八忽,一度半之余切也。长半径(壬戊),四丈七尺七寸六分一厘三毫九丝五忽;心距墙三十三丈四尺一二三四九三(如壬甲),检余切表,得一度四十二分五十一秒卅二微,在日心下二分八秒二十八微(如卯辰);余割三三四二七三五零六(如壬丁)。([10],35页)
图7的右、左两图分别对应图8和图9,其中字母与遗稿天干地支图标相对应,即甲O、乙S1、丙与丁(各出现两次,笔误,现将图7右上图的丙、丁分别记为T、P,左上图的丙、丁依次记为K1、S2)、戊B、己C、庚S、辛R、壬M、癸N;子W、巳K3、申Q、酉K、戌G、亥V;乾B1、坤C1。原文未标注的,为对称与行文方便,加标字母。
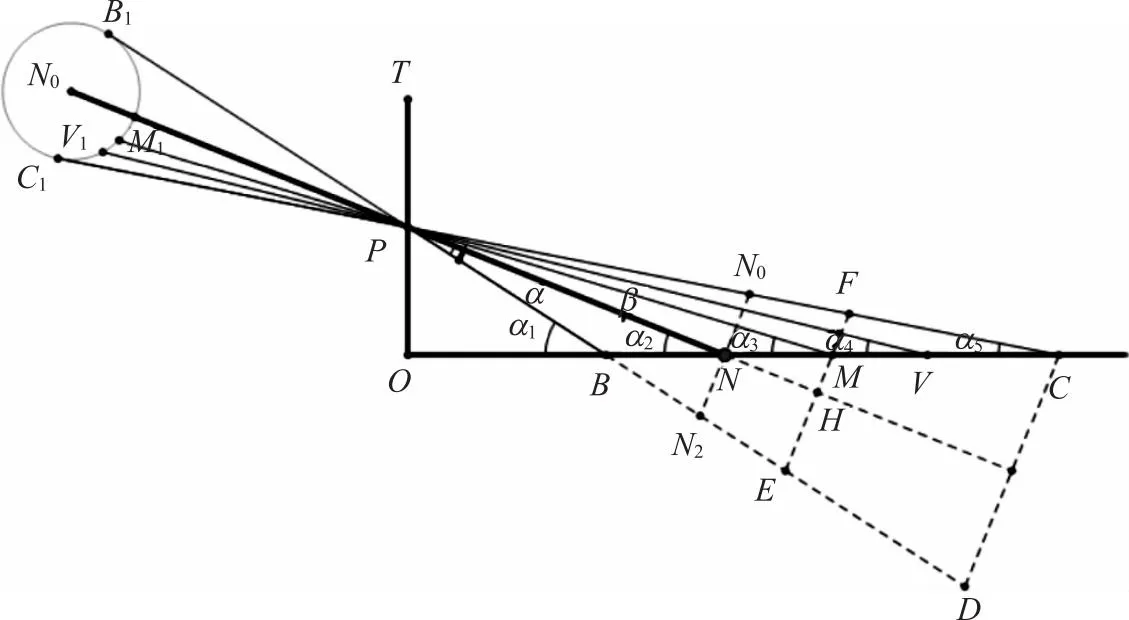
图8 日影投射及作辅助线求椭圆短半径示意图
如图8,设日高α2=1度45分,日半径角α=15分,即角∠B1PN0或∠BPN。N为日心N0的射影,B,C分别为日上、下边沿射影,BC即投影椭圆的长轴。OP=1(5)原文此处单位为丈,与前述一样,长度系十进制,直接用数字表示,涉及长度的数字单位略。,cotα1=OB=28.6362498,查表知α1=2度,cotα5=OC=38.1885288,查表得α5=1.5度。M是BC的中点,因此BM=(OC-OB)/2=4.7761395。cotα3=OM=OB+BM=33.4123493,查表得α3=1度42分51秒32微。

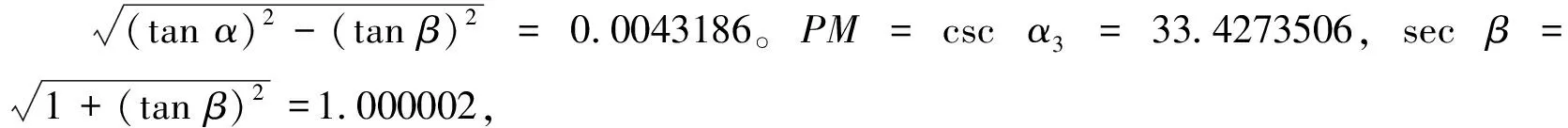
另PN=cscα2=32.7455510,NN1=PNtanα=0.1428787,NQ=NN1 图9 投影椭圆及辅圆 图10 图9之原图 如图9,以椭圆中心为圆心,分别以椭圆的半长轴a、半短轴b为半径的圆称为辅圆。 考虑椭圆的横弦与横径之比。记∠K1MS1=θ,cosθ=GK3/MK3,又GK3/MK3=VK/MS,将前已算出的VK、MS数据代入,得cosθ=0.9897491,查表得θ=8度12分39秒4微。 考虑椭圆的纵弦与纵径之比。sinθ=MV/MK1,又MV/MK1=UK/MC,而UK=MV=MN,MC=BM,将前已算出的MN、BM数据代入,得sinθ=0.142816,查表亦得θ=8度12分39秒4微。 “以幂积论”采用计算面积的方法,验证等式SCMS1/SS1MK1=SCMS/SSMK成立,证实“椭圆形面圆锥斜剖所成与圆柱斜剖所成,其边周无所盈缩,其同为正椭圆审矣”。从这句话来看,时人有可能认为“圆柱斜截面”是“正椭圆”、“圆锥斜截面”是“不正的椭圆”。事实上,由椭圆面积公式,有SCMS1=πa2/4、SCMS=πab/4,故SCMS1/SCMS=a/b;又根据椭圆基本定理SS1MK1/SSMK=a/b,等式成立,说明邹伯奇知晓椭圆基本定理、面积公式等内容。 “谨按以椭圆影揆日高度”,说明太阳的天顶距或地平高度与其晷影长度可以互求[20],影长值计算时还需考虑蒙气正(清蒙差)。 郭守敬从测影工具、测影方法方面改进圭表测影技术,景符与横梁的结合使用,确实大大提高了测量精度。然而,真的是“不容有毫末之差”吗?邹伯奇发现郭氏测量理论存在瑕疵,或许源于对数学与光学的研究,熟悉椭圆知识与小孔成像原理等数理知识,敏锐地意识到投影椭圆的中心并非日心,并进行实证与论述。20世纪80年代初,郭盛炽等在实际测量中也发现了这一问题[21],意识到按郭法所测的影长并非hcotθ,而是hcot (θ-δ)(图8,∠ONP=θ,∠OMP=θ-δ),并借助一个纸屏辅助测量以获得δ的近似值,从而使测量值近似等于hcot (θ-δ),但未能从理论层面深入分析,目前有关圭表测影研究文献并未采用该法,仍没有意识到它的重要性。可见,邹伯奇的订正成果没有广为人知,除了传播工具落后等历史原因,成果的理论意义与应用价值未被挖掘也是重要因素。 如图8,不失一般性,设P为小孔,BC表示射影椭圆的长轴,M为BC的中点即椭圆中心,N为日心N0在地面的射影。 显然,PN是∠BPC的角平分线,记∠BPN=α,则∠CPN=α;记OB、ON、OM、OC的长度分别为xa、xc、xm、xb,OP的高度记为h;∠OBP、∠ONP、∠OMP、∠OCP分别简记为θ1、θ2、θ3、θ4,∠NPM记为δ,θ2即日距地平高度简记为θ,故θ1=θ+α,θ2=θ,θ4=θ-α。以l表示影长,旧法取OB为影长,即l=xa;郭法取OM为影长,即l=xm;邹法取ON为影长,即l=xc。 旧法选择的测影点为B,在日心射影点N的左边(南边),郭法选择的测影点为M,在点N的右边(北边),即旧法偏左、郭法偏右、邹法适中。若θ与计算理论影长的太阳地平高度(考虑大气蒙气差)相等,则xc=hcotθ正是理论影长,影长表达式与系统误差如表1。因此,邹伯奇日心观测模型是对郭守敬圭表测影理论的完善。 表1 三种日影测量方法的影长表达式与系统误差 不难发现,该三种影长满足关系: 又tanθ1=h/xa,tanθ4=h/xb,用正切二倍角公式,得 将④式代入③式,即得②式。②式看似复杂,计算系统误差xm-xc也不便捷,但可清晰看到真实值并非以椭圆心为测影点。事实上,xc可化为xc=xm-atanαcotθ⑤,其中a=(xb-xa)/2表示投影椭圆的半长轴。 邹伯奇椭圆影心非日心模型,既是郭守敬“圭表测影”测量理论的完善化,也为日影测量的误差分析提供新的重要判据。 从定性角度看,若测量误差为零,则xa 从⑥式可知,在固定的测量地点,日半径角α不变,冬至时投射角θ达到最小,cotθ达到最大值,投影椭圆的长径2a也达到最大值,此时系统误差atanαcotθ达到最大值,夏至测量时反之。这就是“即使采用景符,测量冬至影长的误差仍远远高于测夏至时的误差”之原因。 郭法虽不完美,但取椭圆中心进行测量,实践中较易施行,但采用冬至圭表测影导致郭法的“缺陷”部分被放大,为何由夏至测影改为冬至测影,典籍中没有记载,好在横梁的使用,使测影点落在以椭圆中心为心的小邻域U(xm,ε)内,测量误差控制较好。 研究发现,约在1844年前后,邹伯奇采用具体实例数值与一般性算法相结合推演结论的论证方法,基于轴线不过椭圆心定理,建立椭圆影心非日心模型,订正了长期以来“椭圆影心即日心”的认知错误,并指出日心投影的正确位置,但囿于未刊行而迄今少为人知。邹伯奇这一成果,是郭守敬圭表测影理论的完善,为日影测量误差分析等提供了新视角。 致 谢邹伯奇玄孙邹忠廉先生惠赠相关资料,内蒙古师范大学郭世荣教授、中国科学院自然科学史研究所邹大海研究员、天津师范大学高红成教授及匿名专家悉心指点,谨致谢忱!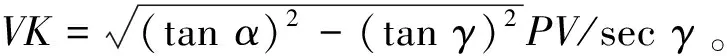


3 邹伯奇椭圆心非日心模型的意义
3.1 郭守敬圭表测影理论的完善





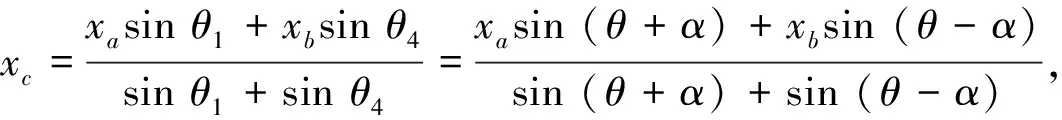
3.2 日影测量误差分析的新判据
4 结 语
