堆叠卫星的分离与重构动力学研究
2024-01-29孙加亮张晓亮金栋平
孙加亮, 张晓亮, 金栋平
(南京航空航天大学 航空学院 航空航天结构动力学及控制全国重点实验室, 南京 210016)
0 引 言
航天器在轨服务为组装大型空间结构以及航天器部署后的维修等任务提供了有效手段[1-2].卫星自主组装是航天器在轨服务的有效手段之一,同时也是建造大型空间结构的重要方法.建造如大型空间望远镜、太阳能电站等大型空间结构时[3-4],常常需要组装几十颗甚至上百颗卫星模块.但是受目前火箭整流罩尺寸的影响,用于自主组装的多颗卫星只能以堆叠状态排列,以高效利用整流罩空间.堆叠卫星系统入轨后先分离再组装,需要设计合适的卫星堆叠方案,充分利用整流罩的空间,在卫星以堆叠状态入轨后分离[5-6],最终再设计合适的组装策略,使卫星能根据既定的方案组装成目标构型.
目前,对堆叠卫星分离过程的动力学已经有了比较详细的研究[7-8],但是部分研究仅针对卫星分离过程,缺少入轨后的卫星组装过程.对于卫星组装过程研究更为广泛,如Lu等[9]使用伪谱法进行卫星之间的避障,Morgan等[10-11]、Foust等[12]研究了使用模型预测控制结合序列凸优化方法进行卫星的运动和路径规划.但是,以上研究关注点均在于卫星组装时的路径规划和运动控制方面,并且只考虑了卫星入轨后的运动组装过程,没有对卫星从堆叠构型分离、组装全过程的动力学方面进行研究,也没有考虑卫星组装后相互之间的锁定约束对运动状态的影响.因此,有必要研究卫星从堆叠状态入轨后分离,再到组装成目标构型的全部过程.
另外,目前通常采用Euler法、四元数等方法建立卫星的动力学模型[13-14],这些方法对于各个卫星之间多个坐标系间的转换计算较为繁琐.而且当卫星组装成目标构型时,无法直观地处理卫星在组装对接过程中的变拓扑约束关系.相比之下,采用自然坐标方法建模[15-17]不仅能避免卫星之间繁琐的坐标转换,同时也能直观地处理堆叠卫星在分离和组装过程中的时变约束.
本文采用自然坐标法建立堆叠卫星系统的动力学方程,设计了合适的卫星堆叠分离方案以及卫星分离后的组装策略,在考虑卫星组装过程中锁定约束情况下,研究了卫星从堆叠状态入轨后的分离,再到按照既定的策略组装成目标构型的全部动力学过程.
1 堆叠卫星系统动力学建模

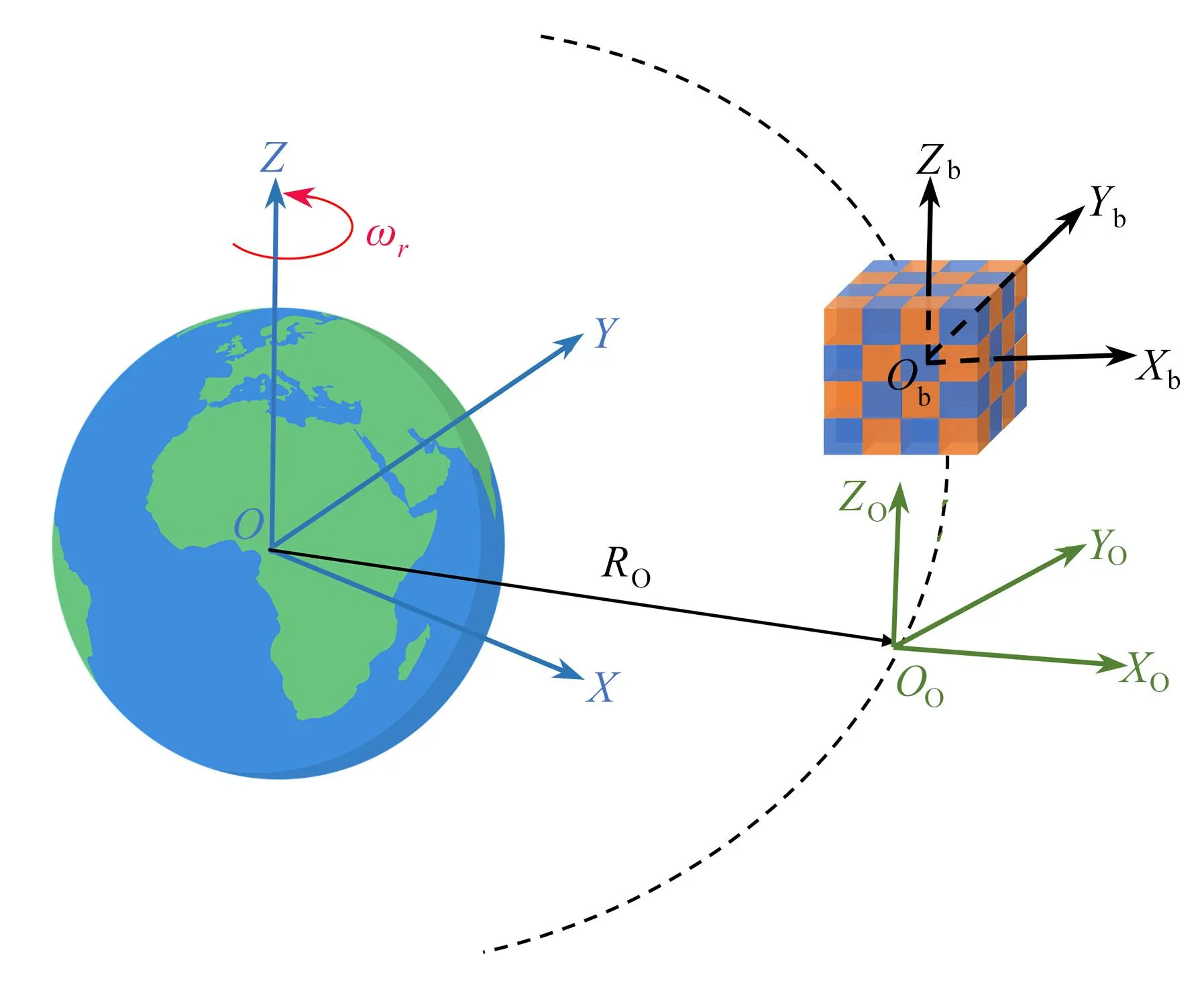
图1 堆叠卫星系统的描述坐标系
惯性坐标系OXYZ中的OZ轴指向地球的自转方向,OX和OY轴位于地球的赤道平面上.轨道坐标系OOXOYOZO中的OOZO轴与OZ轴平行,OOXO轴沿着卫星初始构型边长的方向,并且始终绕着OZ轴以恒定的角速度ωe=0.001 144 rad/s转动.本文研究的堆叠卫星系统由64颗卫星组成,每颗卫星的质量M=62.5 kg,卫星均是边长a为0.5 m的立方体.
1.1 单颗卫星动力学建模
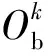
(1)
(2)

图2 卫星k的自然坐标
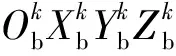
(3)

(4)
其中,矩阵Ck为常数矩阵.因此可以推导点P的速度和加速度分别为
(5)
卫星k的质量矩阵根据虚功原理[18]可以得到
(6)
卫星k中的固有约束有6个,分别是
(7)
当两颗卫星分离前和对接后,卫星之间为固接约束,每两颗卫星通过对接机构锁紧后将会存在6个约束方程,以m,n两颗卫星为例,他们之间的约束方程为
(8)

1.2 堆叠卫星系统轨道系动力学建模
在惯性坐标系OXYZ中,堆叠卫星系统的动力学方程可表示为如下的微分代数方程组:
(9)

为更好地在轨道坐标系OOXOYOZO中观察堆叠卫星系统的运动,通过坐标转换,得到堆叠卫星系统在轨道坐标系下的动力学方程为[8]
(10)
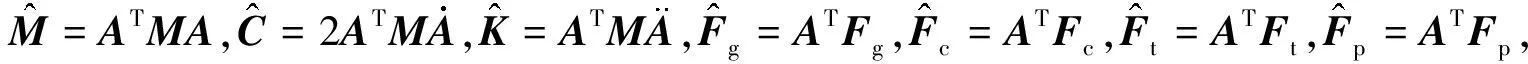
qa=Aqo+R.
(11)
(12)
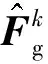
本文采用广义α算法[16]求解式(10)所表示的系统动力学方程.
2 堆叠卫星系统重构组装控制算法
2.1 控制力
为了使卫星始终向目标位置移动,对卫星施加控制力.假设卫星k的初始和最终时刻的广义坐标分别为
(13)
考虑到卫星运动时速度的变化,设置卫星k运动的吸引力为[19]
(14)
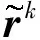
2.2 避障力
为了避免卫星运动之间的碰撞,设置避障函数.以m,n两颗卫星为例,m,n两颗卫星之间的排斥势为
(15)
其中,rm,rn分别表示m,n两颗卫星质心的位置,d和δ分别代表危险和避撞区域的半径,
纸瓦楞是瓦楞夹芯结构被推广应用于包装科技领域而出现的一类非金属多孔夹层结构和材料,具有质量轻、比刚度/强度大、抗冲击性能高、成本低、工艺简单等优点,在军工/民用产品防护与包装工程领域都有很重要的应用价值,还可代替传统的木质材料及其包装[1- 3]。在产品包装防护系统中,纸瓦楞作为缓冲吸能结构,被合理地放置于包装箱和产品之间,通过自身的压缩变形与缓冲吸能作用来实现产品保护与安全运输[2,4]。
避障力为排斥势的梯度,可以写为
(16)
其中,rmin表示两颗卫星之间的最小距离.
为了能使用优化方程寻找两颗卫星之间的最小距离,可以把卫星外形描述为一个连续可微函数[8].以第m颗卫星为例,卫星外形可以表示为
(17)

判断两颗卫星之间的最小距离问题可以等价于求解以下凸优化问题:
(18)
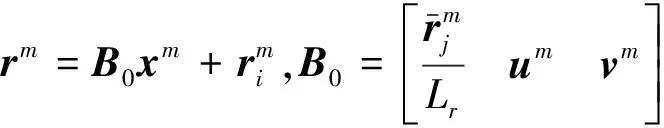
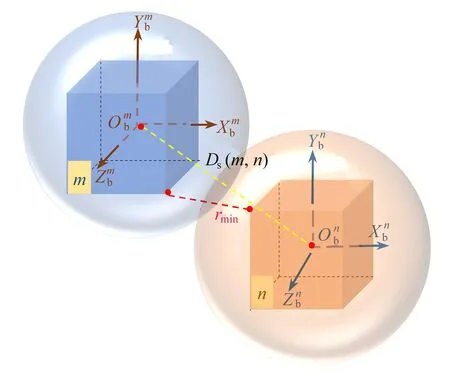
图3 卫星之间的最小距离与卫星中心的距离
2.3 控制力矩
为了消除自旋分离导致卫星姿态的变化,使卫星能够达到期望的姿态,方便卫星组装,对卫星施加控制力矩.结合PD控制,设置控制力矩为
(19)
其中,kpt,kdt分别表示姿态控制系数和角速度控制系数.产生的力矩对应的广义力为[20]
(20)
其中
3 堆叠卫星系统分离与组装策略
3.1 初始构型和目标构型
堆叠卫星系统由64颗卫星组成.考虑到火箭运载能力以及整流罩体积限制,需要设计合适的卫星堆叠初始形状,使卫星能够占据较小体积.因此设计如图4(a)所示的堆叠卫星构型,64颗卫星在初始时刻预先堆叠排列,形成一个结构为每层16颗,共4层的立方组合体.本文所设计的卫星目标构型为如图4(b)所示的分形结构.首先,卫星由初始构型分离之后,卫星每8个一组,组成8个单元,最后8个单元组成整体构型.
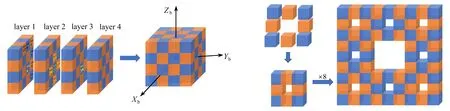
(a) 初始堆叠构型 (b) 目标组装构型(a) The initial configuration (b) The final configuration图4 堆叠卫星初始构型与目标组装构型
3.2 分离与组装过程
堆叠卫星系统分离与组装过程如图5所示.首先,卫星由运载器发射进入指定轨道;然后,由初始堆叠构型缓慢自旋,目的是通过离心力使卫星相互无碰撞分离;最后,当卫星通过自旋展开互相分离后,将进入组装阶段,64颗卫星首先组装成8个相同的卫星模块,然后8个卫星模块再组装成最终构型.

图5 卫星分离组装策略
4 动力学仿真分析
4.1 自旋分离过程仿真
堆叠卫星系统在轨分离有很多种方式,如在卫星层间施加弹射力、通过卫星整体自旋分离等.本文使用给卫星施加一定方向的自旋角速度方式进行一次性分离.施加的角速度可以表示为ω0=[ωXOωYOωZO]T.通过仿真计算,本文采用的堆叠卫星系统的初始分离角速度为ω0=[-0.1 -0.35 -0.2]Trad/s,分离阶段所用时间为40 s.从图6可以看出,尽管堆叠卫星系统在分离阶段发生较大的旋转和大范围运动,但是整个分离过程中并没有发现碰撞现象.

(a) t=0 s (b) t=5 s (c) t=10 s

(d) t=20 s (e) t=30 s (f) t=40 s图6 分离阶段卫星构型
以第二层的22号卫星为例,与其相邻的卫星编号分别为6号、18号、21号、23号、26号和38号.图7表示22号卫星与其相邻卫星之间的最小距离曲线.可以看出,该卫星与相邻卫星之间的距离呈现出不断增大的趋势,卫星在分离阶段没有发生碰撞,说明采用的自旋角速度是合理可行的.

图7 分离阶段22号卫星与其相邻卫星之间的距离
4.2 重构组装过程仿真
安全无碰撞分离之后,再对堆叠卫星系统进行重构组装,重构组装不同阶段的控制参数如表1所示.
图8表示组装过程的动态构型图,可以看出,堆叠卫星系统在分离后,依次按照设计的组装策略,实现阶段2、3、4构型.
由于8组卫星的运动状态基本上是同步的,因此这里只分析第一组卫星,即1~8号卫星的位移与速度变化.图9表示卫星沿着OXb,OYb,OZb轴三个方向的位移变化曲线.在前40 s,卫星处于分离阶段,沿着各个方向的位移均逐渐变大.随后,由于控制力作用,卫星运动逐渐平稳,并运动到目标位置且保持稳定.

表1 控制参数的取值

(a) t=70 s (b) t=150 s (c) t=220 s

(d) t=250 s (e) t=283 s (f) t=360 s图8 组装阶段卫星构型
为了更直观地显示姿态控制器的效果,同时更便于理解,简化计算,本文使用卫星连体坐标系ObXbYbZb与轨道坐标系OOXOYOZO中三个轴之间对应的夹角表示卫星的姿态,即使用ObXb与OOXO之间的夹角χ、ObYb与OOYO之间的夹角ξ以及ObZb与OOZO之间的夹角ψ表示.设轨道坐标系三个轴对应的单位向量分别为xo=(1,0,0)T,yo=(0,1,0)T,zo=(0,0,1)T,以第k颗卫星为例,
(21)
姿态变化如图10所示.姿态变化主要集中在前60 s.卫星的自旋分离导致姿态不断变化,经过自旋分离阶段之后,由于姿态控制器的作用,卫星的姿态能够很快稳定下来,并且在之后的阶段中,始终处于较平稳的位置.

(a) OXb方向的位移 (b) OYb方向的位移 (c) OZb方向的位移 (a) Displacements in the OXb direction (b) Displacements in the OYb direction (c) Displacements in the OZb direction图9 1~8号卫星的位移

(a) χ (b) ξ (c) ψ图10 1~8号卫星的姿态
图11表示卫星沿着OXb,OYb,OZb轴三个方向的速度变化曲线.值得注意的是,在260 s、310 s左右产生速度的突变,这是由于卫星在这些时刻进入对接距离并施加固定约束所致.在整个过程中,速度并没有超过0.5 m/s,处在合理的范围之内.

(a) OXb方向的速度 (b) OYb方向的速度 (c) OZb方向的速度 (a) Velocities in the OXb direction (b) Velocities in the OYb direction (c) Velocities in the OZb direction图11 1~8号卫星的速度
图12表示施加在卫星上的控制力、控制力矩以及避障力曲线.根据仿真结果可以看到,整个过程中,控制力和控制力矩均不超过10 N,而避障力只在少数时间段存在,这也表明了设置的控制器是合理有效的.

(a) 控制力 (b) 控制力矩 (c) 避障力(a) Control forces (b) Control torques (c) Avoidance forces图12 1~8号卫星上的主动力
5 结 论
本文针对由64颗卫星组成的堆叠卫星系统分离重构问题,研究了卫星从堆叠状态分离释放、到分形重构组装的整个动力学过程.卫星由堆叠状态入轨后,通过施加ω0=[-0.1 -0.35 -0.2]Trad/s的自旋角速度,实现卫星无碰撞分离.另外,本文还设计了卫星组装策略,将卫星分离组装全部过程分成4个阶段,使卫星能够按照预定的步骤实现组装.在卫星组装过程中,通过PD控制,并且结合势函数设计控制器,既能避免卫星之间的碰撞,又能使卫星在320 s左右较为高效地运动到目标位置.为了处理卫星组装系统中的时变约束,本文采用自然坐标方法建模.最终通过数值仿真对堆叠卫星从分离到组装的全过程进行分析,结果证明卫星整体分离组装过程不超过360 s,控制力均在10 N以下,卫星能够按照既定的步骤完成分离重构.以上结论表明,本文所设计的卫星组装策略是合理的.
致谢本文作者衷心感谢南京航空航天大学科研与实践创新计划(xcxjh20220107)对本文的资助.
