基本流纬向切变下的稳定辐射斜压位涡
2024-01-29刘楠,宋健
刘 楠, 宋 健
(内蒙古工业大学 理学院, 呼和浩特 010051)
0 引 言
自20世纪80年代以来,位涡(PV)理论是研究大气海洋学的重要概念,引起大气海洋学研究者们的广泛关注.PV理论之所以得到科学界的重视,是由于它是大气海洋学的一个基本性质,常用于判断大气海洋的特性.涡流依赖于平均PV梯度,同样也适用于PV理论,可以充分表明大气海洋中的不稳定性.PV表示两邻近等熵面(等位温面)之间的大气柱在被带到某一规定纬度并被伸缩到某一规定厚度时所有的涡度.涡流主要产生于东部边界上升流系统和巴西洋流区域,随着纬度的大幅增长而逐渐减弱[1].其中涡旋即是涡流遇到纬向及经向诱导速度等外界因素引起的旋涡.中高纬度地区,在大尺度下,大气海洋运动学中的涡旋在基本纬向流嵌入大规模垂直切变下的不稳定性影响是一个极其重要的研究方向[2].在斜压大气下,基本纬向流通过垂直切变的影响会转化成涡旋,在绝大多数大气海洋系统中均出现类似于双曲正弦的潜在涡度/流函数,其呈现出双涡旋状态[3].王爽等在其所研究的流体流动产生的垂直速度分量,同样导致涡旋的形成[4].Flierl的线性计算结果表明,涡旋在受到斜压扰动后,向西移动的同时会辐射 Rossby波,然而不存在衰变的情况.对于涡旋的移动速度, 会呈现色散关系, 发生色散会使其衰减得很快, 与之相反的是当涡旋受到一个非线性的影响时, 依然可以清晰地显现出Rossby波的传播轨迹[5].Arbic和Flierl提出在质量上将无黏性和自由衰变的流动,扩展成分层、强迫和耗散的流动[3].通常情况下在Rossby波稳定辐射下的斜压涡旋导致向西或者向东纬向传播的一个结果[6].
Flierl通过上层、下层流体分别为浅水和准地转(quasi geostrophic,QG)模式研究了辐射涡旋[5].准地转表示在涡度方程中,除散度项外其他各项引入地转关系而计算的大气大尺度运动.Pakyari和Nycander发现,在普遍情况下,涡旋的传播速度取决于“hetonic”机制,即由上层涡流和下层涡流之间的水平移动,其结果是,涡旋向东行进趋于稳定; 而涡旋向西行进则恰好相反,即体现涡流的不稳定性[7].穆穆通过大气动力学理论证实了大气运动的基本模式-正压与斜压准地转模式强解存在唯一性[8].Sutyrin和Dewar发现涡流是在上下两层结构不对称性的偶极相互作用,或作用在两层之间进行耦合传播[9].Held和Larichev在亚热带向西流动中发现寿命最长的海洋涡旋[10],斜压涡旋在嵌入大规模垂直剪切流中产生可以与β平面上的惯性Taylor柱(inertial Taylor columns)相关的Rossby波相反符号的涡流[11].惯性Taylor柱表示在旋转流体中作缓慢移动的柱体上方,存在一个惯性与此柱体一起移动的流体柱.Sutyrin和Hesthaven等研究了长期演化的单极涡和偶极涡在PV大尺度梯度(β效应)影响下,采用等效气压准地转方程进行了数值求解[12].通常情况下,受到辐射的斜压涡旋向西移动,这些向西传播的涡流,其较长寿命的特点在纬度带上占据首要地位[13].Sutyrin在水平中深度下,研究了地球中物理涡的寿命长短,其研究成果展现出基本涡流参数之间的另一种联系,这种涡旋的强化机制起到相当大的作用[14].在β平面近似下,陈利国等分析发现,影响非线性Rossby波的重要因素中包含推广的β效应及切变基本流[15].然而,这些研究仅限于基本垂直切变中Rossby波的振幅在两层模型中的简单演化,仍缺乏完整性[16].
Flierl[5]和Larichev等[17]进一步推导了在无黏性的情况下,获得了准地转上下两层方程的解析解.Phillips两层模型中,由于上下两层之间的平均准地转PV(QGPV)梯度符号不同,引起斜压不稳定性,而Charney模型的不稳定性是由平均表面的温度梯度以恒定状态的内部PV梯度β相互作用带动的[18].通过层状模型继续讨论大气海洋的斜压不稳定性[19].在β效应平面上,基于上下两层Phillips模型,在大尺度下垂直剪切中,通过对涡流稳定流动解析解的数值模拟,讨论了基本流在Rossby波稳定辐射下纬向流二次切变的情况,给出了二次切变基本流对稳定辐射斜压PV的影响.
本文描述了稳定辐射下的斜压PV模型,基于Rossby波的产生,涡旋速度逐渐减慢.从而使斜压下产生的这种波动和涡流效应形成新的位势现象.涡旋产生的Rossby波,在纬向和经向上稳定传播,还会引起经向涡旋传播轨迹流以及相干的热流.基于β效应平面上的两层模型,讨论了Rossby波的稳定性,若上层的PV梯度为正,则经向传播会导致涡旋逐渐减弱.因此,当PV梯度较弱时,涡旋仍能传播很长一段距离,直到振幅越来越弱,释放捕获流体并逐渐使涡旋消亡.证实了上层PV梯度的减少延长涡旋的传播能力,总结了纬向基本流二次切变下的斜压PV受扰动情况.利用Bessel函数找出了数值解.对于亚热带海洋向西流,降低上层PV梯度会持续延长涡旋的寿命.本文研究了这种变化的其中一种形式,即纬向基本流在二次切变下对稳定辐射斜压PV的主要影响.
1 控 制 方 程
斜压大气模式下准地转模型为[20-21]
(1)
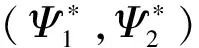
(2)
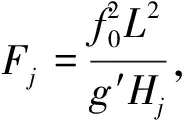
2 基本纬向流二次切变的斜压PV色散关系
根据正交模方法,设扰动流函数为
(3)
由方程(2)获得色散关系:
ω2[k4+k2+(l2+F1+F2)+l2F1]+ω[k3(2a1+2a2+β1+β2+uF1-uF2)+
k(2a1l2+2a1F2+2a2F1+β2F1+β1F2+β1l2-ul2F1)]+
k2(4a1a2+2a1β2+2a1uF2+2a2β1+β1β2+uβ1F2-2a2uF1-uβ2F1-u2F1F2)=0.
(4)
在不考虑黏性项的两层基本流中, 采用两层斜压模式[22].纬向二次切变引起上下两层斜压流体的不稳定性,在向西行进中,考虑u=-1,然后对ω与a1,a2的两种色散关系进行讨论.
首先,a1=0,a2≠0时,ω与a2之间的关系如图1所示,a2=0,a1≠0时,ω与a1之间的关系如图2所示.当a1=0或a2=0时,在所选区间里,图1与图2中基本纬向流走向大致相同.纬向切变下的涡旋在二次剪切流中呈现上升趋势,且在二次切变下,涡旋向西行进的传播速度逐渐平缓,在一段时间内保持稳定状态传播.由于基本流向西行进的同时辐射Rossby波, 但却不衰减, 斜压涡旋处于稳定辐射下, 为了进一步阐明二次剪切流对斜压流体不稳定性的影响, 基本纬向流在二次切变中, 若其中一层的PV梯度为零时, 则经向传播导致涡旋呈现上升趋势, 且上升速度逐渐趋于缓慢, 在上升到一定程度时,会趋于稳定状态向西行进.这表明在二次切变的影响下, 基本流发生明显变化, 深入演化二次剪切流对稳定辐射斜压流体的主要转换过程.

图1 当a1=0, a2≠0时,ω与a2的关系
其次,当a1≠0或a2≠0时,基本纬向流在二次切变下先是呈急剧上升趋势,到达峰值后迅速减弱(图3、4),上下两层PV梯度中的扰动流均在平流层中,在涡旋经向峰值处,纬向基本流随二次切变的影响,涡旋向西行进的传播速度逐渐加快.由图中显示:当a1≠0时(图3)纬向流向西行进的速度很明显要滞后于当a2≠0时(图4)纬向流西进速度,即二次切变扰动后,a2对纬向基本流的传播具有冲击力,而a1对纬向基本流传播的影响相对较弱.这表明斜压下涡旋在二次切变下是纬向向西传播的,由于Rossby波稳定辐射使其始终向西行进[23].
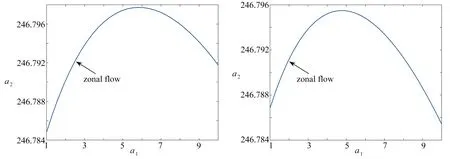
图3 当a1≠0时,a1对ω与a2关系的影响
若不考虑两层的PV梯度和斜压流体的变动,二次剪切流中关于y的扰动流ω与涡旋上层涡流a1,下层涡流a2的色散关系如图5所示.关于二次剪切流对相干具有较长寿命涡流的影响,在基本流纬向切变下,扰动流的气压和影响气压成分在上下两层是相互补偿的.在斜压下,二次剪切流可以持续延长涡旋的寿命.上层涡旋的传播轨迹主要是向南,由于涡旋略微滞后于向西流动的背景流,因此也有向西的成分.而下层涡旋由向东移动的涡流主导,并且为上层相干涡旋的经向传播提供了有利条件.位于上层PV梯度的气压斜涡旋在二次切变下几乎是不稳定的,同时在深海层中增强PV梯度会影响Rossby波的轨迹流.因此,纬向基本流在二次切变下对稳定辐射斜压涡旋的不稳定性影响是有迹可循的.
上述数值模拟充分表明了垂直切变下的斜压流体存在的不足之处,即不能清晰地刻画出涡旋在斜压下的主要变化过程.于是,对于纬向流在稳定辐射下的斜压流体来说,将垂直切变深入转化为二次切变无疑是一个更加充分的说明.
对于大波数,k2+l2≫F1,扰动集中到下层,纬向相速度向西略微靠近,并且低于下层背景流速.对于小波数,k2+l2≪F1,纬向相速度大幅度向西,表明正压下的扰动,上下两层涡流速度与颗粒位移大致相同,于是纬向相速度处于-∞<ω/k 图5 ω与a1,a2的三维关系 F1ψ1+(∇2-β/c)ψ2=0. (5) 而在上层,q1必须依赖于坐标系中的流函数,并且随着涡旋平移,定义F1ψ1+cy-uy≈F1ψ1,令q1=Φ(ψ1),得到 (∇2-F1)ψ1+F2ψ2=Φ(ψ1)=q1, (6) (7) (∇2-γ2)φ1=q1(r), (∇2+γ2)φ2=q1(r). (8) 两层的流线通过式(5)和(6)表示,ψ1和ψ2由下式给出: (9) 其中 (10) 在无限域中,涡旋向西行进之前,即x→-∞.无黏性的流体受到向西扰动的条件制约.因此在极坐标下容易解出扰动流向西延伸过程中的解析解,通过Bessel函数解出φ2,φ2可以写成 (11) (12) 将其应用于渐近解知 (13) 斜压流体的经向传播速度通常从涡旋向西运动过程中获得,下层Rossby背风波模式的中心最大值相对于上层涡流中心向东平移.推导出式(13)的解析解用作数值模拟的初始条件.这种方法消除了细尺度β环流典型的圆形涡流,没有Rossby背风波. 本文采用理想两层模型与相关数值模拟,研究了在大尺度二次剪切流中忽略黏性嵌入斜压涡旋,分析了二次剪切流对稳定辐射斜压涡旋的不稳定性影响以及涡旋的寿命长短.在研究中发现,二次剪切基本流与涡流的色散关系再次证实了基本纬向流切变可以引起斜压不稳定性.利用Bessel函数的数值解可以解释斜压流体向西运动引起斜压涡旋,且不断产生Rossby波.纬向基本流体现出一个有趣的例子,即Rossby波的传播轨迹由其所在的背景流产生,同时还提供了维持Rossby波传播所具备的条件.因此,在大尺度大气海洋中,基本流二次剪切是引起斜压涡旋不稳定性的主要原因,且二次切变下的扰动流影响涡旋寿命的延续,对延长涡旋寿命有重大意义. 本文通过两层大气模式,采用上下两层涡度对Rossby波振幅的色散关系进行了研究.采用Bessel函数数值近似解的方法,考虑了中高纬度,纬向基本流在二次剪切下,对稳定辐射斜压PV的不稳定性影响.刻画出二次剪切流中Rossby波振幅与上下两层涡流的演化及其色散关系.研究发现:Rossby波随纬度变化的走向是纬向二次剪切流中诱发斜压PV不稳定性的因素之一,同时在二次切变下基本纬向流U(y)对斜压流体的不稳定性存在影响,以及对涡旋寿命的延伸起到一定的作用.


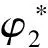
3 结 论
