水电机组摆度周期性波动问题的分析和研究

2024-01-29李志华汪安海徐楠楠曾学杰周科衡

大电机技术 2024年1期

李志华,汪安海,徐楠楠,曾学杰,万路,李虎,周科衡

(1.西安热工研究院有限公司,西安 710032;2.华能澜沧江水电股份有限公司,昆明 650206)

0 前言

“双碳” 目标背景下,水力发电在电网系统承担调相、调频、调峰的优势日益凸显,对机组安全稳定运行的要求也越来越高。上机架是水电机组上导轴承径向受力的传递构件,上导摆度大、上机架振动超标等问题在电厂频繁出现,相关学者对此进行了深入的研究[1-4]。二滩水电厂通过频谱分析和动平衡试验对上导摆度超标问题进行了分析[5],发现匝间短路造成的不平衡磁拉力是导致上导摆度超标的主要因素;紧水滩水电站采用轴线调整、受力与中心调整和发电机气隙调整等方法有效地解决了上导摆度超标问题[6];王建等人通过对上机架刚度不足引起的振摆特征进行分析,发现上机架千斤顶的错误安装方式可引起刚度不足和机组振摆超标[7];李延频等人采用动平衡试验方法处理了三门峡水电站3 号机组发电机振摆超标的问题,并取得了较好的效果[8];毛子首等人分析了上机架和定子系统刚度引起的机组振动特征及动态特性[9];张军等人从工程实践角度出发,总结了钢结构连接方式的优劣,客观分析了焊接热影响区、残余应力、低温冷脆等缺点对机组振动的影响[10]。关于燃煤、核电及抽蓄机组的振动和摆度治理研究也有很多,且取得了较好的动平衡治理效果[11-15];一些学者和技术人员还结合工程案例从信号的处理、故障诊断、振摆算法等角度对振动和摆度进行了分析计算,为电站故障诊断和振动问题的处理提供了参考依据[16-20]。由上述研究现状可知,关于机组上机架振摆超标的原因分析和处理措施的文献已有很多,但是影响机组上导轴承摆度呈周期性波动的因素涉及电气、测量、机械、金属材料、安装施工等不同领域,目前相关的分析研究相对较少。

基于此,本文以某水电站机组为例,从上导摆度峰峰值和平均值测量原理出发,通过机组运行参数进行验证,得出上导摆度峰峰值呈周期性波动是由大部件金属结构的非对称蠕变造成的结论,且详细地记录了分析过程。

1 问题描述

某水电站安装有4 台混流式水轮发电机组。机组轴系由三段组成,自下而上分别为水轮机主轴、发电机主轴和滑转子,发电机采用密闭自循环空气冷却系统,现场5 瓣组圆,自并励静止可控硅整流励磁装置。上机架支臂为14 个,呈螺旋状沿中心体外缘均匀分布,支臂径向中心线和上机架中心体切线的夹角为76°。现场装配中心体和支臂,并将其焊接为一体,支臂和基础板之间采用工字钢过渡并与基础板把合,上机架结构如图1所示。

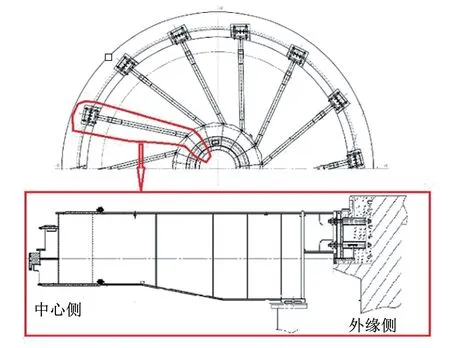
图1 机组上机架结构示意图

该电站自首台机组投产以来,发电机组上导轴承摆度存在如下异常波动规律:上端轴摆度峰峰值随时间在24h 内呈正弦变化规律,具体如图2所示,波动峰值出现在6∶00～9∶00 时段,谷值在17∶00～19∶30 时段。当4 台机组停机后再次开机,从开机至并网的短时间内表现不尽相同,但是在带负荷连续运行24h 以上时,上端轴摆度峰峰值均出现周期性波动,且运行时间越久,4 台机组表现的波动规律和幅值越一致;同时,对比同一台机组的摆度数据发现,夏季波动幅度低于冬季波动幅度。以上异常现象困扰着电站技术人员,且会影响设备的安全运行。

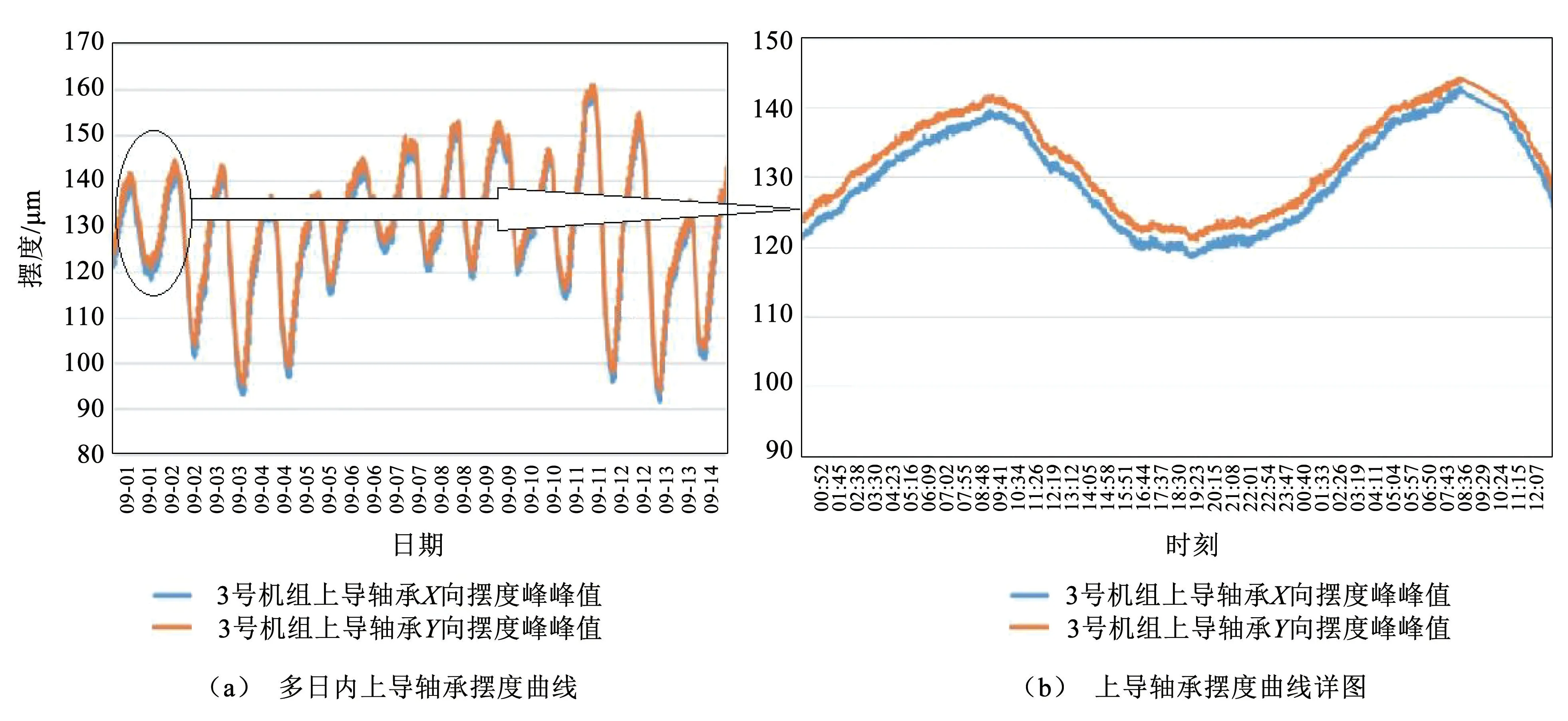
图2 机组上导轴承摆度多日和日间摆度波动曲线

2 问题分析

为了分析4 台机组上导轴承摆度峰峰值呈周期波动的原因,首先从摆度峰峰值的测量基本原理和测量系统构成出发。主轴摆度峰峰值是指发电机在运行过程中,主轴相对固定部分的间隙极值大小,其测量系统包括信号采集系统和传感器信号系统。其中传感器信号系统由非接触涡流探头、固定托盘支架以及信号传输线缆等组成。根据传感器系统构成,则可知主轴摆度间隙峰峰值的变化情况,主要有以下3 种表现形式:(1)主轴晃动幅度不变,探头基座位置变化;(2)探头基座位置不变,主轴晃动幅度变化;(3)探头基座位置变化且主轴晃动幅度变化。这三种情况均可能会出现采样起止时刻和摆度起止时刻不重叠的情况,根据峰峰值的计算原理可知,如果采样起止时刻和摆度起止时刻重叠,则主轴摆度间隙峰峰值不受基座蠕变的影响;如果采样起止时刻和摆度起止时刻不重叠,则主轴摆度间隙峰峰值会受探头基座蠕变的影响,且随着探头基座向主轴蠕变,峰峰值会变小,反之则变大。

为了进一步判断表现形式(1)～(3)哪种更加接近机组轴系摆度峰峰的真实变化规律,以4 号机组为例进行了测试。在4 号机组上机架中心体油盆底部X向加装临时涡流探头,并将上机架Y向涡流探头更换为带温度补偿的涡流探头,而上机架X向探头不做任何改动,时刻记录机组带负荷运行时上导摆度的峰峰值,测量结果如图3所示。图中X向摆度为原探头测量数据,Y向摆度为油盆底部X向新加装探头测得数据,下导Y向摆度为上机架Y向带有温度补偿的涡流探头测得数据。

图3 4 号机组不同测点数值变化

从图3 中可以看出油盆底部探头测得摆度峰峰值周期性波动消失,并且带有温度补偿的探头测得的数据依然存在周期波动。经过反证法和排他性因素分析,上导摆度波动符合主轴晃动幅值不变,探头基座位置发生变化,即符合表现形式(1)。

3 动静态数据分析

为了分析验证探头蠕变产生的部位和可能原因,根据上机架结构特点和探头安装位置,技术人员现场测量了机组在停机状态下,基坑温度、油盆盖板和主轴之间间隙、上机架支臂与基坑之间的间隙三个量的变化。临时测点布置如下:在基础板焊接探头支架安装非接触涡流探头,在支臂外缘处焊接直角金属贴片,测量二者的间隙(以下称“间隙1”),用于表征机架径向间隙和蠕变量,并实时记录基坑温度。为了测量上机架支臂在X方向和Y方向的蠕变值并验证涡流探头测量结果的可靠性,分别在X方向和Y方向支臂与基础之间增设机械百分表,其测量结果分别称为“间隙2” 和“间隙3”,机械百分表只可监测静态上机架间隙的蠕变过程数据。非接触涡流探头及机械百分表的具体布置如图4 和图5所示。

图4 4 号机组非接触涡流探头安装位置示意图

图5 4 号机组机械百分表安装位置

发电机基坑周围主要材料为基坑钢板内衬和钢筋混凝土,且根据混凝土和金属的物理特性可知,上机架金属部件的热传导率及线性膨胀系数约为混凝土的50 倍,并且钢板内衬厚约35mm,因此基坑内基础板的位移和蠕变相对较小、较慢,在数据分析时可看成死点。

3.1 静态数据分析

根据图4 和测量原理可知,机组在停机下记录的间隙数值反映了机组上机架和基础板之间的相对距离,且通过分析可知,基坑内基础板的位移和蠕变相对较小较慢,因此该相对间隙可认为是上机架的蠕变量。4 号机组2022年1月19～23日处于停机状态,监测间隙1 和基坑温度的变化,结果如图6所示。

图6 4 号机组基坑温度和间隙1 变化曲线

4 号机组在1月19～23日处于停机状态,停机后基坑温度持续降低,由原来的27.5℃降至21.5℃,变化接近6℃,间隙1 由起始的580μm 降至410μm,总历经时间为110h。从图6 中可以看出,间隙1 和温度随时间的增加呈类线性下降趋势。具体数据为:1月19日02 ∶00,温度和间隙1 分别为27.6℃和586.5μm,1月20日02 ∶00 温度和间隙1 分别为25.6℃和556.5μm,间隙1 在24h 内变化了30.0μm,温度变化了2.0℃;1月22日15∶00,温度和间隙1分别为22.7℃和446.0μm,1月23日15∶00 温度和间隙1 分别为21.6℃和411.5μm,间隙1 在24h 内变化了34.5μm,温度变化了1.1℃。

人工读取4 号机组上机架X、Y向百分表测量的间隙数值,绘制相应的温度、间隙变化曲线,如图7和图8所示,根据测点布置的位置,图中“ -” 表示向内侧移动,“ +” 表示向外侧移动。

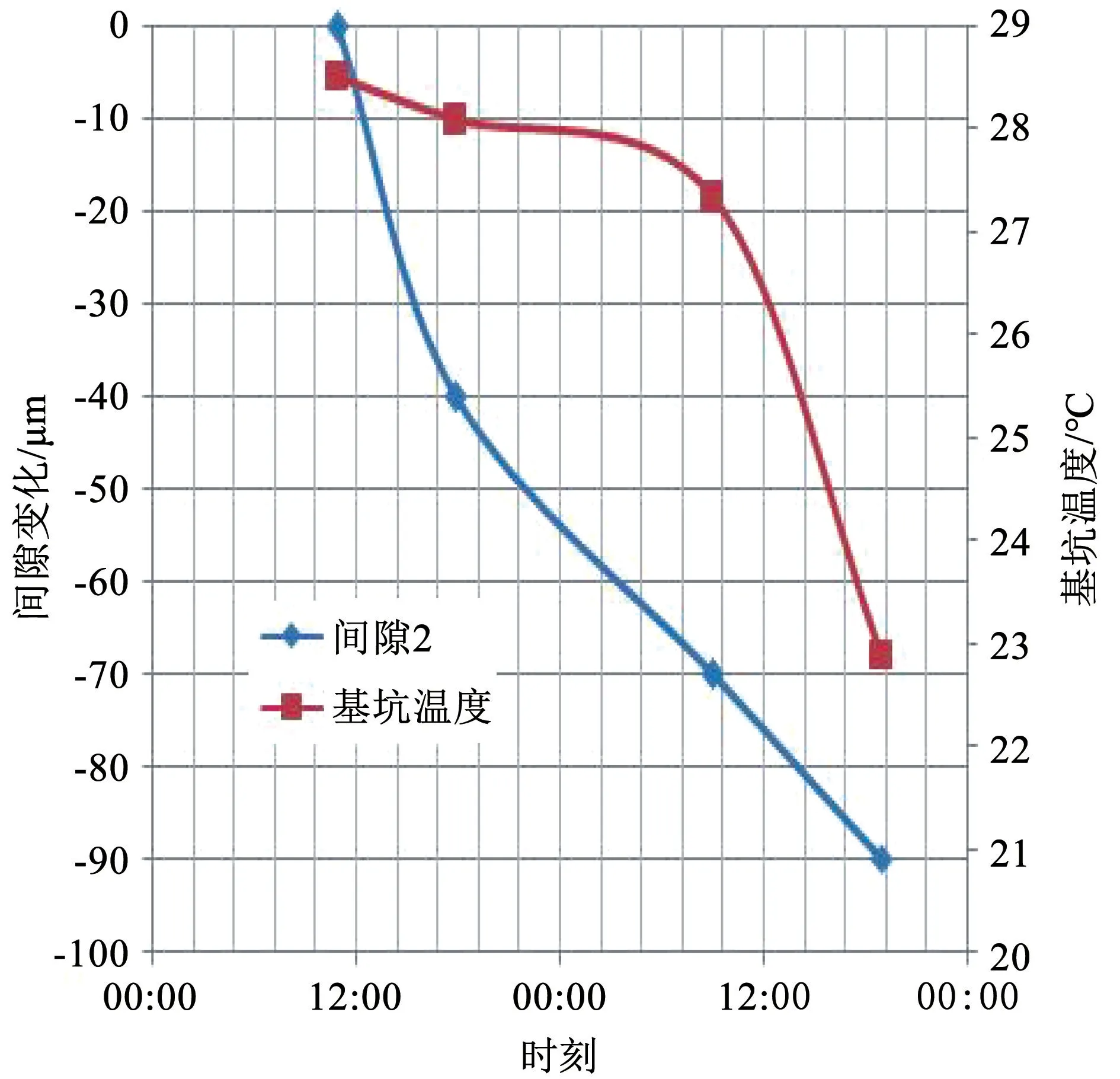
图7 间隙2 及温度的变化曲线(X 向)

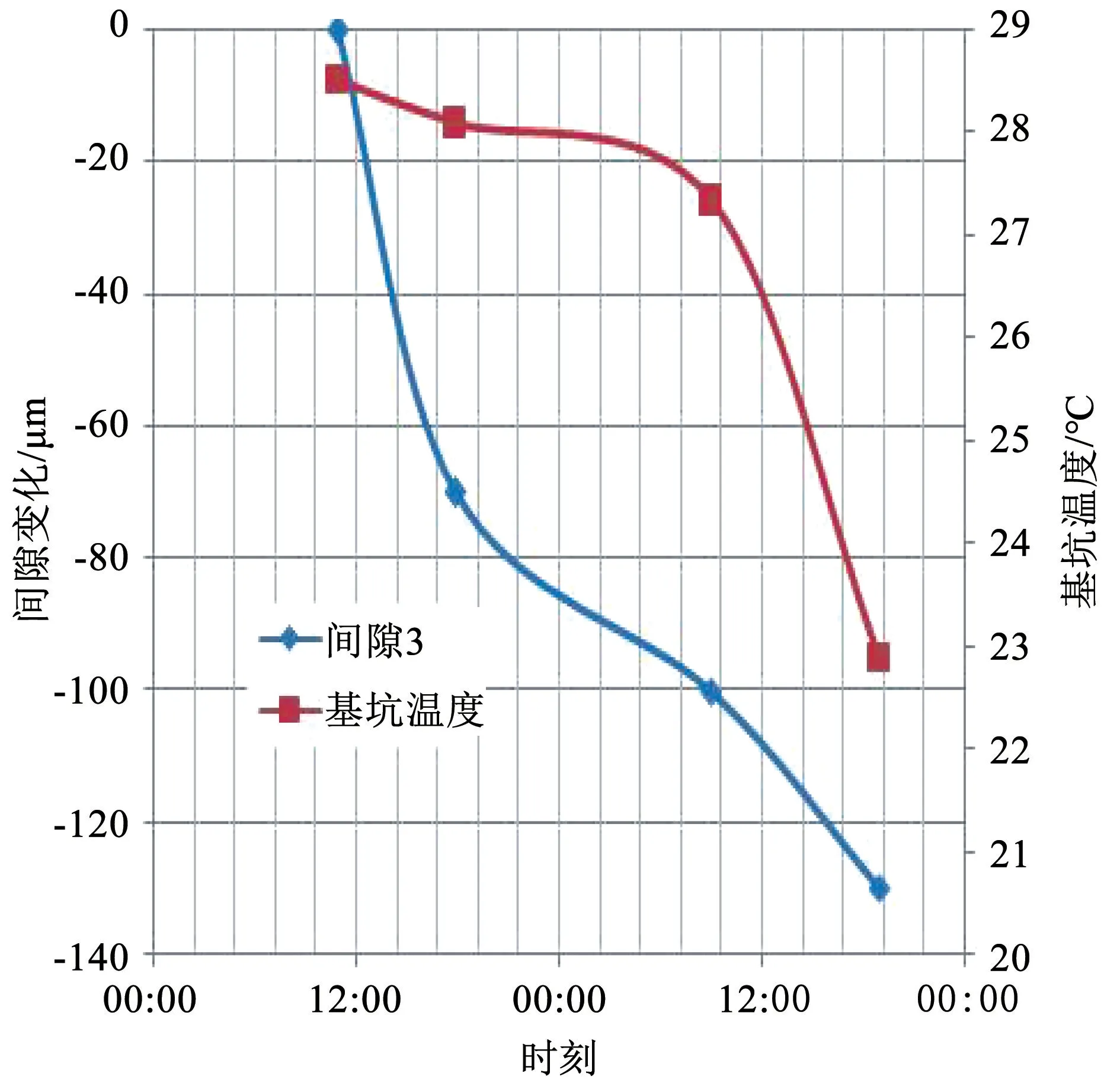
图8 间隙3 及基坑温度的变化曲线(Y 向)

从图7 和图8 可以看出,上机架X、Y向间隙2、间隙3 及温度均随时间的增加呈下降趋势,该变化趋势与间隙1 变化趋势相同,数值相近。X向和Y向支臂与基础板之间的间隙缩胀量并不一致,Y向较X向大40μm,即X向和Y向支臂在相同温度变化时出现了非对称蠕变。

通过静态数据分析可知,机组上机架随基坑温度下降而产生蠕变,表现规律为:间隙1 随基坑温度的降低而减小,即温度越低,间隙越小,基础板和机架支臂的距离越小。机械百分表测得的数据变化趋势和涡流探头测得的数据规律一致,方向相同,但机架X向和Y向的蠕变量不一致。

3.2 瞬态过程数据分析

4 号机组在2022年1月17日和23日分别启动并网带负荷运行,其中17日启停两次,分别为10∶00和16∶00,23日启停一次,为15∶00,间隙1 和基坑温度随机组启动的瞬变过程如下。

启动中和启动后基坑温度符合如下规律:机组启动中因通入冷却水,基坑温度迅速由25℃降低至18℃;机组并网后,随着发电机电磁发热、鼓风发热、摩擦发热等发热量的增加,抑制了基坑温度下降的速度,基坑温度最终维持在15℃±0.5℃范围。启动过程中基坑温度经历了先快速下降,而后缓慢下降,最终维持在某一发热和散热的平衡状态。停机后基坑温度符合如下规律:机组惰走期间,基坑温度先由15.6℃经5min 上升至17.6℃,后经5min 上升至19.87℃,再经5min 上升至20.0℃,又经70min 上升至25.5℃,随着金属部件、转子和定子等蓄热的持续释放,最终维持在26.5℃。待发电机上盖板、下盖板和风洞处的热辐射交换量大于蓄热部件释放的热量后,基坑温度开始缓慢下降,停机后,基坑温度经历了先快后慢下降,再稳定的温度变化规律。因蓄热部件的热量释放和基坑盖/壁周围的热辐射交换均比较缓慢,所以停机温度变化较启动时缓慢的多,具体数据如图9所示。

机组启动时,间隙1 并未发生明显改变,经5min后间隙1 值由539μm 升至545μm,后经历15min 降至416μm,再经历15min 持续降至382μm,之后缓慢下降,最终维持在360μm±5μm,间隙1 从开始变化至最终稳定共持续了约90min,大概呈现了先升后降,先快后慢并经较长时间稳定的变化规律。机组停机后惰走期间,间隙1 由376μm 升至447μm,机组完全停稳5min 后,间隙1 升至461μm,后经5min 升至468μm,再经5min 升至473μm,又经70min 上升至497μm,随着基坑内新的热平衡的建立,间隙1 数值也逐渐升至513μm,并随着基坑温度的稳定而稳定。通过瞬态过程数据的分析可知,基坑温度变化和间隙1 变化一一对应,即温度高间隙1 变大,温度低间隙1 变小。

根据静态数据间隙1、间隙2、间隙3 随温度降低而减小,瞬态数据间隙1 随温度升降而增减且变化幅值和温度变化一一对应,可以得出,当机架和基础板之间的间隙1 变小,则支臂和中心体(大部件金属构件)沿径向向外侧蠕变;当机架和基础板之间的间隙1 变大,则支臂和中心体沿径向向内侧蠕变。

3.3 运行数据统计分析

作者统计了该电站4 号机组2021年9月的运行数据,主要有调速器导叶开度、机组有功功率、无功功率、冷却水温、上导瓦温、空冷器冷热风温度、油槽油温、上机架振动等数据,发现只有集电环室温度与上导摆度一一对应,且相关性较强,具体数据如图10所示。

图10 4 号机组摆度和温度变化关系

集电环室通过格栅窗口与厂房内空气形成热交换,因此集电环室温度一定程度上反映了环境温度,特别是负荷工况无明显变化长周期运行后,环境温度和集电环室温度一一对应。从图中可知,机组摆度最大出现在环境温度最低的早上,摆度最小则出现在环境温度最高的下午。考虑到空气辐射换热的迟滞性和惯性,集电环室的最低及最高温度一般较环境温度晚2～3h,因此上导摆度最大值出现在8∶00 左右,最小值出现在17∶30 左右。