基于定子全浸式及绕组内冷式的蒸发冷却永磁直驱风力发电机优化设计研究

程自然,阮 琳,杨 劼,高 剑,黄守道

(1.湖南大学电气与信息工程学院,长沙 410082;2.中国科学院大学,北京 100190;3.中国科学院电工研究所,北京 100190)

0 前言

我国幅员辽阔,风能资源分布广,总量十分丰富,具有良好的开发和利用前景,同时风力发电作为风能捕获中最主要的利用形式,其容量等级和技术水平正伴随着我国“双碳” 目标下绿色发展和低碳建设脚步的稳步迈进而持续提升。因此,风力发电机作为风电机组中重要的机械-电磁能量转换设备,在风力发电系统中也发挥着不可或缺的作用,其技术水平也亟待得到进一步地提高[1]。作为我国自主研发的电气装备冷却技术,自循环蒸发冷却技术采用不燃不爆的氟碳工质作为冷却介质,自上个世纪五十年代以来,已经在许多电气装备应用领域中取得了优异的成果[2-5]。除相变换热所具有的热负荷自适应性以及高效的散热性能以外,其特有的自循环系统还具有无需外部驱动和易于维护等优点[6],是未来大容量直驱式风电机组冷却方案的理想选择。

然而,伴随着风电机组单机容量的不断增长,其损耗和发热问题将愈发严重,散热条件也将随之不断恶化,严重时将影响风力发电机的正常运行甚至引发事故,同时电机热负荷的提升也与冷却性能的改善密切相关,因此提高风力发电机的散热性能对于风电机组安全性和可靠性的提升以及机组小型化和轻量化的发展有着十分重要的意义。对此,国内外已有许多学者针对这些问题开展了研究,文献[7]基于等效热网络法对永磁风力发电机的温度场进行了分析和计算,文献[8]基于等效热网络法对电机系统的散热量进行了分析,然而从中还无法直接分析得到冷却性能与发电机电磁设计参数之间的关系。文献[9]提出了一种全封闭式自循环风冷系统,并对冷却系统在不同尺寸下的散热性能进行了对比研究,文献[10]通过在机舱外增加辅助散热装置来利用风场的自然风对发电机进行辅助散热,然而风力发电机本体参数在设计过程中没有参与优化。文献[11]基于有限元法对蒸发冷却风力发电机的电磁场进行了分析,文献[12]对大型风力发电机的蒸发冷却技术进行了分析和研究,然而还未基于冷却系统的优势对发电机参数进行优化设计分析。

本文针对蒸发冷却风力发电机定子全浸式及绕组内冷式技术路线的优势和特点进行了对比分析,并以降低电机有效材料的成本和减少工质的用量作为优化目标,对一系列不同功率等级下的直驱式永磁风力发电机进行了优化设计,基于优化结果对两种不同的冷却技术路线进行了对比和分析,进而得到了不同技术路线下冷却系统造价成本随机组功率等级增加的趋势,上述优化分析结果能够为风力发电机的设计和优化提供参考和依据。

1 蒸发冷却风力发电机分析设计模型

1.1 风力发电机定子蒸发冷却技术

风力发电机组通常被设计成水平向上倾斜3°～5°,这为蒸发冷却系统的自循环流动提供了良好的工作环境[13]。针对风力发电机定子而言,其发热位置相对集中且损耗分布较为均匀,因此适合采用空心导线内冷或定子全浸式蒸发冷却技术,相应结构如图1所示。内冷技术需要在原绕组中增加空心导线,通过空心导线内冷却工质的相变和循环流动来实现对定子绕组及铁芯的散热,这种冷却方式对工质的需求量较少,且冷却工质能够与绕组中的发热源进行直接接触,因此有利于绕组的散热。全浸式蒸发冷却技术需要通过外部密封腔将定子完全封装并浸泡在工质中,密封腔整体具有结构简单、有利于模块化装配和制造的特点,然而这种冷却方式对工质的需求量较多,且冷却工质不能和绕组中的发热源进行直接接触换热。

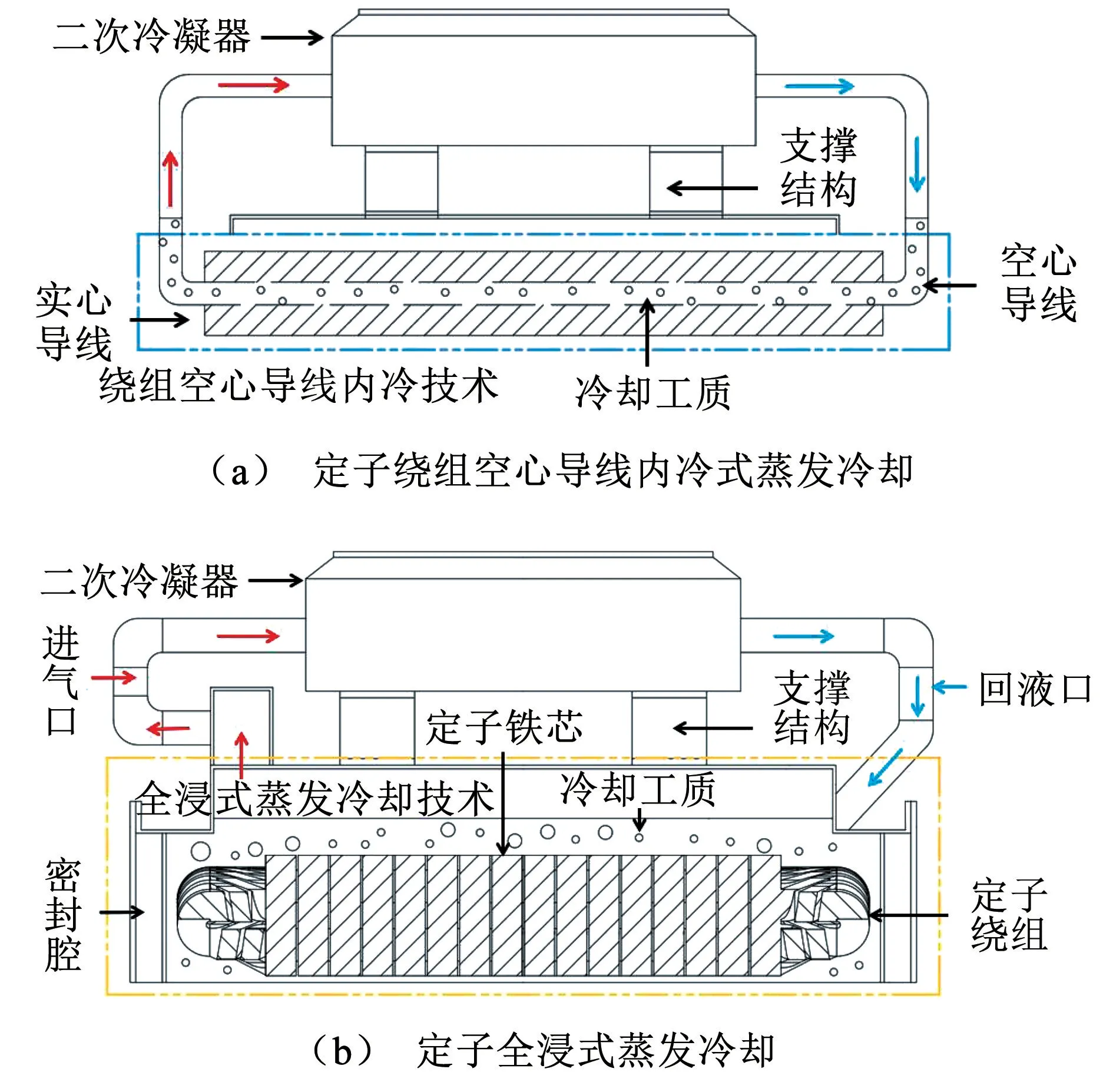
图1 定子蒸发冷却系统结构示意图

1.2 风力发电机电磁方案分析设计模型

在运行过程中,表贴式永磁直驱风力发电机的定子侧通过变流器与电网相连,其相电压和电磁功率受到直流母线电压的约束为:

式中,U1为定子相电压;Udc为直流母线电压;P为输出功率;E0为空载电动势;Xs为同步电抗。

根据交流电机绕组的基本理论,定子每相绕组的电感和电阻值为:

式中,Lms和Lsσ为电枢电感和漏感;R为电阻;μ0为真空磁导率;Lef为铁芯有效长度;rs为电枢半径;Kdp为绕组系数;N为每相串联匝数;p为极对数;geff为气隙有效长度;q为每极每相槽数;λ为电枢漏磁导;ρ为电阻率;Lav为平均半匝长度;a为并联支路数;Ac为绕组截面积。

由永磁体产生的绕组每相空载电动势为:

式中,Br为永磁体剩磁密度;hm为永磁体磁化方向厚度;μr为永磁体相对磁导率;αi为计算极弧系数;n′为转速。

作为发电机定子中的内热源,绕组和铁芯中产生的损耗为:

式中,PCu、PFe和pFe分别为定子总铜耗、定子总铁耗和铁芯单位损耗;I1为定子相电流;σh、σe和σd分别为磁滞损耗、涡流损耗和附加损耗系数;B为磁感应强度;f为频率;Vt和Vy分别为定子齿部和轭部体积。

以上公式构成了永磁直驱式风力发电机电磁参数及损耗计算的分析设计模型。

1.3 风力发电机冷却系统分析设计模型

定子绕组的温度场分布作为冷却系统设计和校核过程中的关键,其传热规律可以基于传热学理论进行研究分析。对于含有内热源的三维导体稳态温度场分布,其导热微分方程应满足:

式中,T为温度;λ′为导热系数;q′为单位体积热能。

针对由蒸发冷却定子铁芯和绕组构成的传热系统,其导热微分方程的通解和特解可以基于第二类和第三类边界条件确定。为了简化分析和计算,同时给冷却系统的设计留有足够的裕量,因此本文中假设铁芯和绕组中的发热损耗完全通过蒸发冷却换热系统带走,同时忽略沿铁芯轴向的温度分布差异,基于物理模型的相似性对冷却系统简化后建立的二维分析计算模型和求解过程中的边界条件设置如图2所示。

模型中温度绝热和对称边界条件设置为:

对流换热边界条件设置为:

式中,h为对流换热系数;Tw为与工质接触的壁面温度;Tf为工质温度;n为边界的法线方向;S2为绝热和对称边界;S3为对流换热边界。

基于已有的实验数据和研究结论[14-15],可知采用常规蒸发冷却工质时,全浸式电机定子腔内工质的等效沸腾换热系数为:

式中,qw为热流密度;p′为工作压力;pr为工质临界压力。

内冷式矩形空心导线中工质的等效沸腾换热系数为:

因此,本文采用冷却工质在不同系统中的等效沸腾换热系数,对不同冷却方案中发电机定子温度场的分布进行分析和评估。

2 基于遗传算法的风力发电机多目标优化设计模型

电机电磁场和温度场耦合的多目标优化设计属于非线性规划问题,其求解难度相比线性规划问题而言更为困难,采用传统的算法往往难以有效地求解得到全局最优解[1,16]。遗传算法基于自然选择策略,通过进化过程中染色体的交叉变异以及对各子代适应度的筛选来获得最优的个体,以此来避免陷入局部最优解,从而能够有效地求解非线性问题,因此本文基于遗传算法对永磁风力发电机的设计参数进行多目标优化求解。

2.1 优化设计模型

为了更好地评估不同功率等级下的风力发电机系统设计成本,本文将电机有效材料的总成本和定子铁芯段冷却工质的总用量作为优化的目标函数,分别设置为:

式中,CFe、CCu和Cm分别为硅钢片、铜和永磁体的单价;GFe、GCu和Gm分别为硅钢片、铜和永磁体质量;Vc为工质体积。其中硅钢片、铜和永磁体的单价与文献[17]中相同,分别取3 欧元/kg、15 欧元/kg和40 欧元/kg。

基于电磁分析设计模型,本文中将优化变量选取为电枢直径、铁芯长度、每相串联匝数、永磁体宽度、磁化方向厚度、实心绕组尺寸和空心导线尺寸(全浸式方案没有此变量)。基于发电机的实际运行要求,设置电磁参数优化的约束条件,见表1。

表1 目标约束条件

在优化过程中,将2MW、5MW 和10MW 直驱式风力发电机的额定运行转速分别设置为22.5r/min、14r/min 和10r/min[1],将极/槽配合分别选取为20 极96 槽、40 极192 槽和60 极288 槽。

基于蒸发冷却系统已有的设计经验[18],在全浸式风力发电机的设计阶段沿定子铁芯轴向段每隔60mm 处设置了一个长度为8mm 的径向流道,在内冷式风力发电机的优化过程中将定子绕组中的最高温度约束条件设置为不超过65℃。

2.2 多目标优化设计求解流程

本文采用带精英策略的非支配排序型多目标优化遗传算法NSGAⅡ对优化问题进行求解,在优化过程中,对于电机设计参数,采用 Ansysworkbench 2021R1 内置的多物理场耦合模块进行耦合分析,求解迭代流程如下:

(1)基于Ansysworkbench 软件建立电磁场和温度场参数的耦合分析模型;

(2)设置初始条件和迭代次数,建立物理分析模型;

(3)产生随机的设计变量初始种群,基于多目标优化函数对其进行非支配型排序;

(4)对筛选后的种群进行选择、交叉和变异操作,产生子代种群;

(5)将子代和父代种群合并,基于多目标优化函数进行非支配排序,并找出相似性较小的个体,形成父代种群;

(6)判断是否满足迭代收敛要求,若是,则输出最优个体的帕累托前沿,否则返回步骤(4),同时增加迭代次数。

2.3 优化方案对比分析

通过多目标优化算法对优化方案进行求解,可以得到一系列并行的可行解,因此本文挑选出两种优化方案中参数较为相近的优化结果进行比较分析。基于优化策略求解得到的优化方案见表2 和表3。

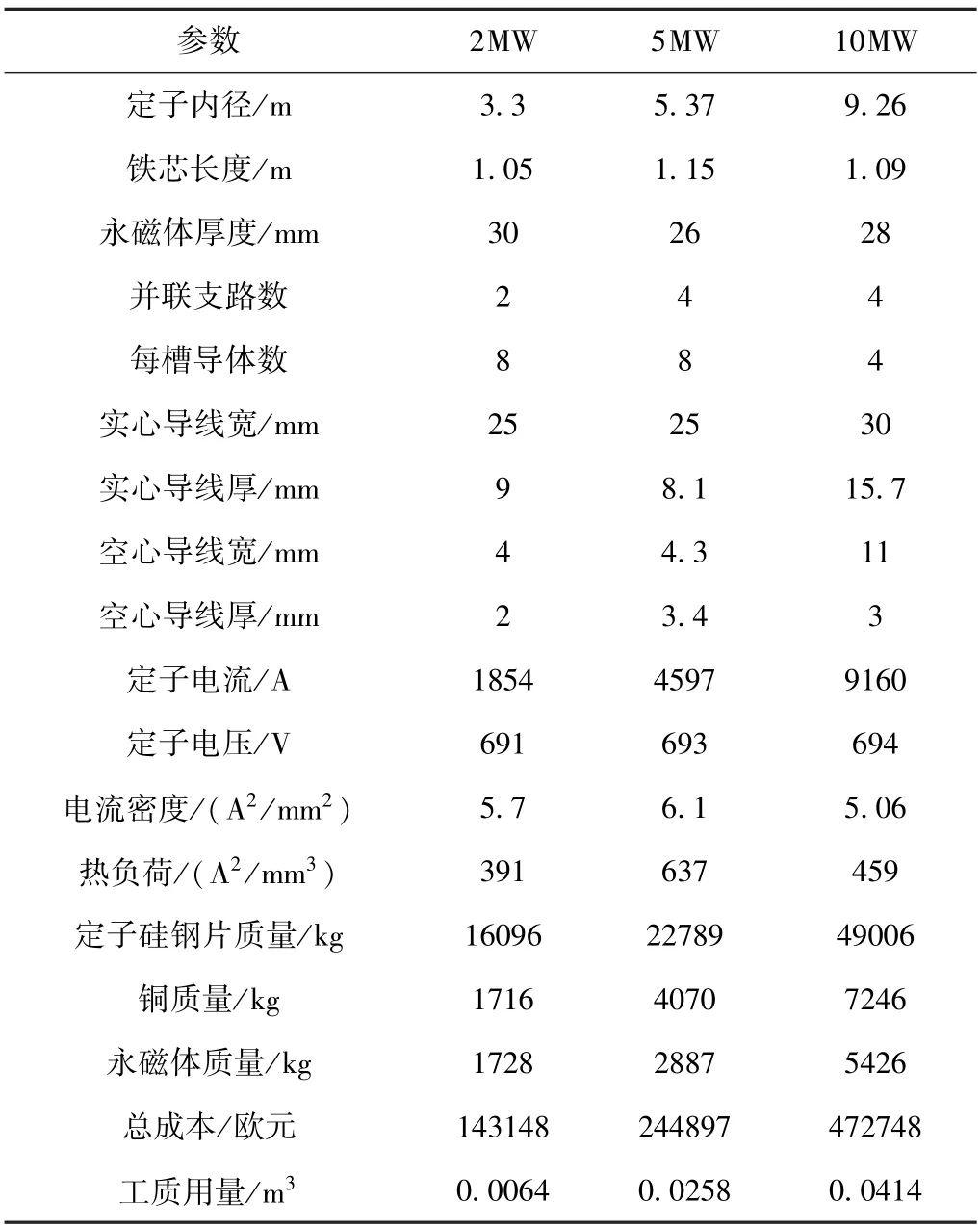
表2 内冷式优化设计结果

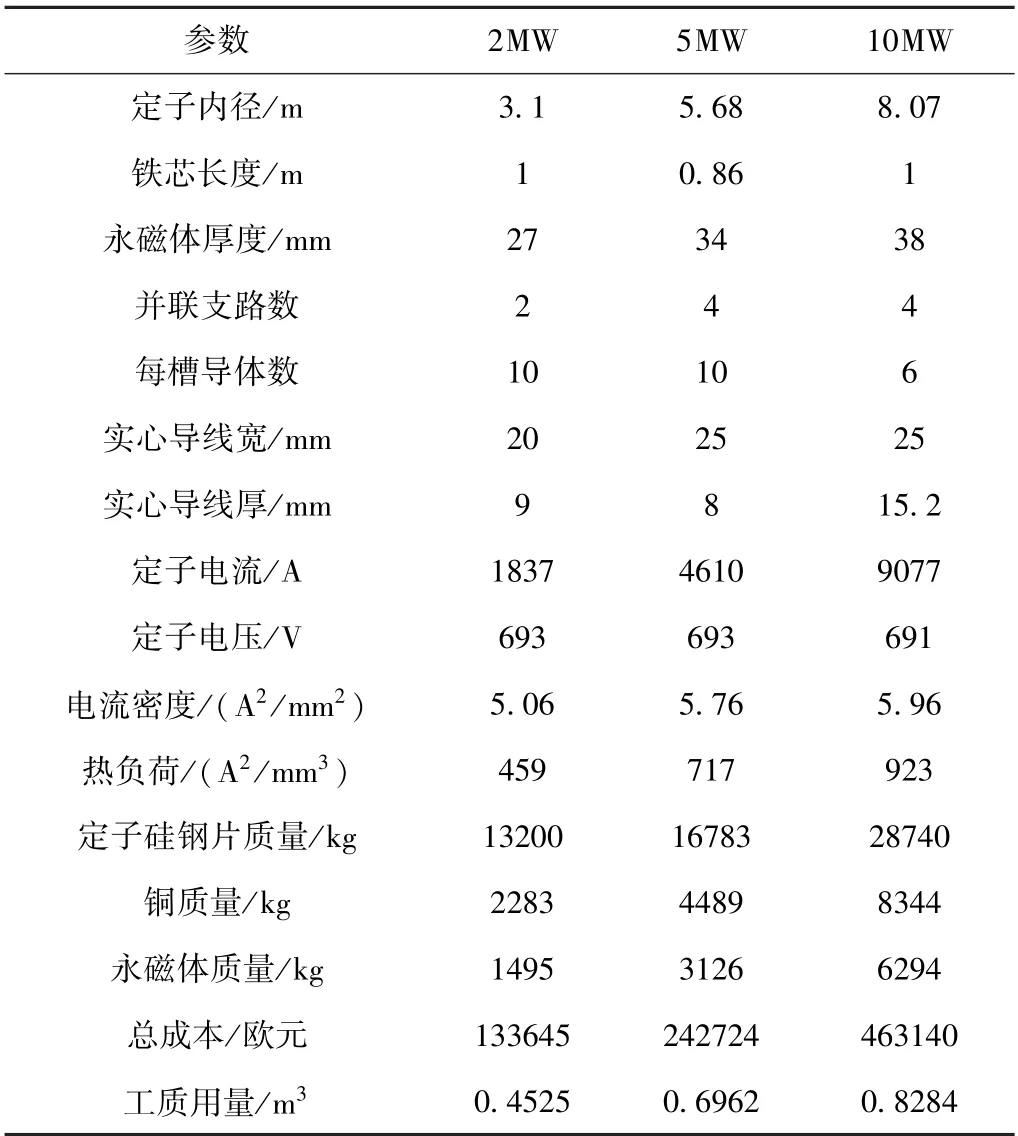
表3 全浸式优化设计结果

从方案对比分析中可以看出,当发电机材料成本相近时,内冷式风力发电机与全浸式相比仅需更少的工质用量,主要原因是此时发电机的外形尺寸较大,导致全浸式方案需要更多的工质来填充定子内部的封闭空腔区域。同时针对全浸式优化方案而言,在设计过程中主要尺寸参数的选取对工质用量的影响较大,针对内冷式优化方案而言,在设计过程中空心导线参数的选取对工质用量的影响较大。

本文选择10MW 风力发电机的优化结果作为分析和验证对象,两种优化方案的多目标优化帕累托分布前沿如图3所示。从结果中可以看出,冷却工质的用量和电磁设计参数在优化设计阶段相互作用并对结果产生影响,因此在电机参数设计阶段应对这两者进行权衡考虑。

2.4 优化结果分析验证

本文基于Ansysworkbench 软件Thermal-state thermal模块对发电机定子的稳态温度场分布进行仿真验证,在仿真计算模型中将铁芯的导热系数设置为40W/(m·K)[14],将绕组的导热系数设置为398W/(m·K),将槽内绝缘的等效导热系数设置为0.15W/(m·K)[19],基于工质沸点将工质的换热温度设置为47.3℃。通过仿真计算得到的发电机定子区域内的温度场分布如图4所示,从计算结果中可知,内冷式优化方案中电机绕组的热点温度满足温度参数的优化约束要求,同时内冷式方案中的绕组和全浸式方案中的绕组相比,前者具有更低的稳态运行温度。

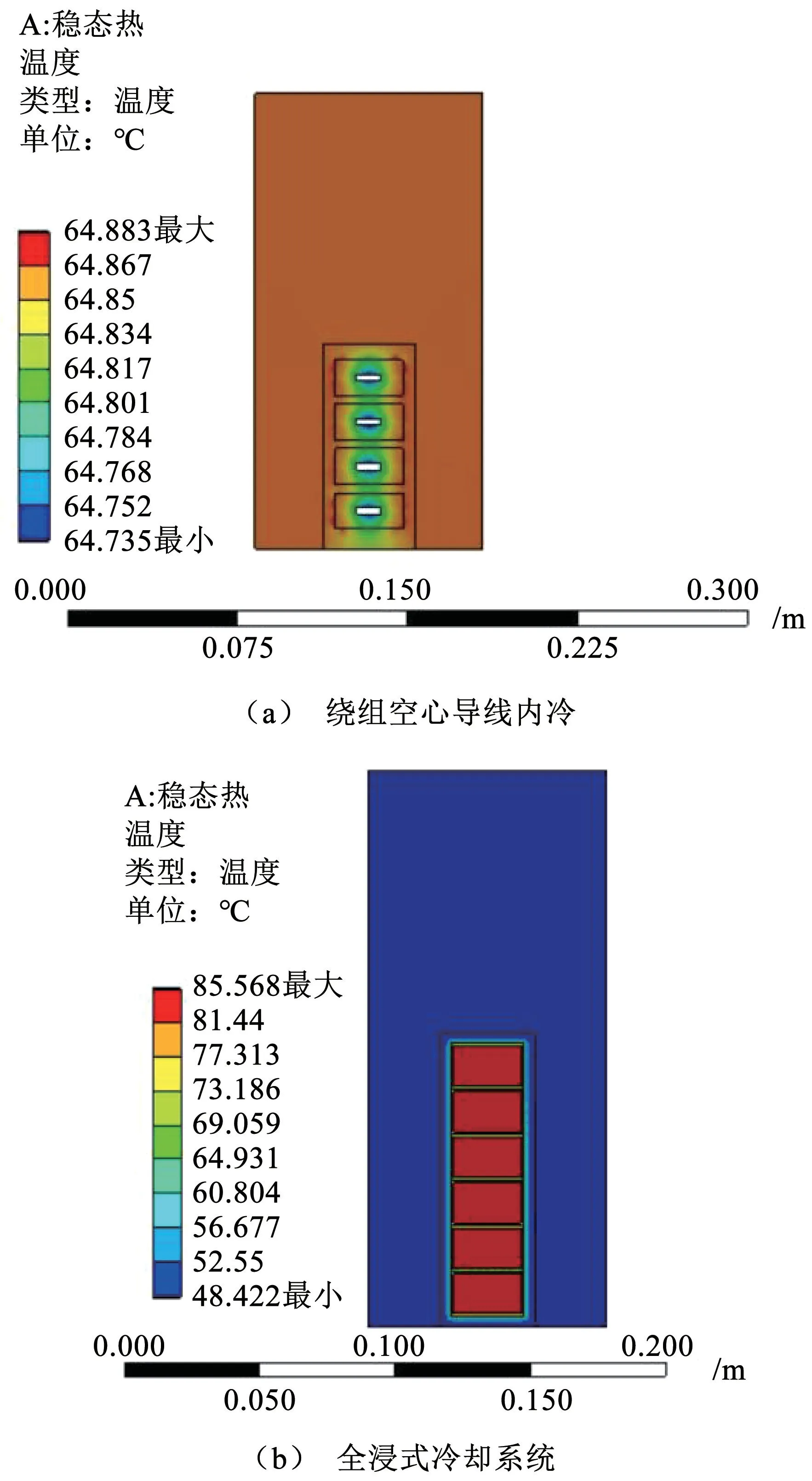
图4 定子温度场仿真验证结果

基于Maxwell 模块对发电机的电磁输出性能进行仿真验证,忽略空心导线在仿真过程中对电磁性能的影响,基于电流密度相等的相似性原则将空心导线模型简化为实心导线模型,基于优化参数建立的永磁直驱式风力发电机仿真计算模型如图5所示,基于Maxwell-2D 瞬态电磁场求解器求解得到额定运行状态下发电机的电磁输出功率和电流波形,如图6 和图7所示。

图5 永磁风力发电机电磁仿真计算模型

图6 电磁输出功率仿真结果

图7 电流波形仿真结果

从仿真计算结果中可知,10MW 全浸式风力发电机优化方案中的电磁输出功率和电流输出波形与有限元仿真结果的误差分别为2.3%和4.7%,10MW 内冷式风力发电机优化方案中的电磁输出功率和电流输出波形与有限元仿真结果的误差分别为2.9% 和3.7%,优化方案能够满足工程设计的误差精度要求。

3 结论

本文基于发电机电磁参数和温度场的耦合分析,提出了一种蒸发冷却永磁直驱式风力发电机优化设计模型,并分别对2MW、5MW 和10MW 三种功率等级下的蒸发冷却永磁风力发电机进行了优化设计,得到了系统材料成本随功率等级增加的变化规律。通过全浸式和内冷式风力发电机优化方案的对比,得到了两种冷却方式在直驱式风力发电系统优化设计中各自具有的特点。最后通过有限元对优化结果进行了验证,结果表明对于兆瓦级直驱式风力发电机而言,采用空心导线内冷技术更具有材料成本和散热性能上的优势,优化结果和分析可以为蒸发冷却技术在永磁风力发电机的设计应用和优化研究中提供理论和基础。