抽水蓄能机组水轮机工况启动过程转轮动应力特性

陈志明,靳发业,林 恺,毕慧丽,王焕茂,罗永要

(1.南方电网储能股份有限公司,广州 510635;2.水圈科学与水利工程全国重点实验室(清华大学),北京 100084;3.清华大学能源与动力工程系,北京 100084;4.水力发电设备全国重点实验室(哈尔滨电机厂有限责任公司),哈尔滨 150040;5.哈尔滨电机厂有限责任公司,哈尔滨 150040;6.哈尔滨大电机研究所,哈尔滨 150040)

0 前言

近年来,我国的抽水蓄能电站建设进入了快车道,并且向高水头、大容量、高转速的方向发展。水头和转速越高,抽水蓄能机组关键过流部件特别是转轮所承受的水压力和离心力越大,对转轮的强度设计提出了更高的要求[1]。与常规机组不同,水泵水轮机作为调峰和调频机组启动和停机非常频繁,有时一天之内达数次,转轮叶片经常处于暂态的水流激振力的作用下,从而使叶片同时承受交变的大幅低频动应力和小幅高频动应力。列宁格勒金属工厂生产联合体在分析水轮机裂纹和可靠性与寿命时进行了叶片动应力测试,结果表明机组开、停机一次对转轮造成的损伤相当于带90%负荷运行80h[2]。因此亟需开展抽水蓄能机组启停机暂态过程转轮的动应力特性研究,指导机组的安全运行。

许多学者对转轮动应力问题进行了深入研究,研究成果为机组的安全稳定运行提供了参考。钱勤[3]和潘罗平[4]分别对不同的水轮机转轮动应力进行了现场试验测量,并对转轮叶片产生裂纹的原因进行了分析。Oishi[5]对高水头水泵水轮机转轮叶片的应力实测表明,转速是影响叶片应力的主要因素,在水轮机工况启动时,动应力随转速的平方上升,到额定转速时应力达到最大。R.Suzuki[6]对水泵水轮机的研究表明,随着转速和水头的提高,作用在叶片上的水压力脉动的幅值和频率都会增加,从而导致转轮的静应力、动应力及其频率都会增加。Nakamura[7]经过实测和分析发现高频脉动在转轮上的应力集中主要在叶片与上冠和下环的交接处,特别是水泵工况在接近叶片出口处(高压侧)。

随着数值计算技术的发展,流固耦合数值模拟技术已逐渐在水力机械转轮的动应力计算分析中得到了应用,郑小波[8-9]将不同时刻叶片表面的动水压力加载至混流式水轮机单个叶片进行了动应力的计算研究,结果表明最优工况点叶片上的应力波动要小于其他工况点。肖若富、王正伟[10-13]等对水轮机进行了全流道非定常流动计算,并在非定常水力载荷基础上,用耦合方法分析了转轮动应力与运行工况的关系。杨敏[14]、高江永[15]等针对双吸离心泵叶轮、轴流泵叶轮进行了流固耦合分析,得到了叶轮在不同工况的动应力和变形等特性,在此基础上进行了疲劳寿命预测。李永恒[16]利用双向流固耦合的方法,得到了水轮机转轮动应力的变化幅值,通过对结果的分析发现转轮应力和变形近似做周期变化,且周期和叶片与导叶数有关。何玲艳[17]研究了水体附加质量对稳态工况水泵水轮机转轮动应力特性的影响,结果表明,水体附加质量不仅显著影响转轮动应力幅值,还会改变结构动态响应的频率。李萍[18]对高水头水泵水轮机动静干涉引起的稳态工况转轮动应力进行了计算分析,结果表明活动导叶通过频率是转轮动应力主要频率成分。桂中华[19]采取稳态和局部瞬态相结合的方法研究了水泵水轮机启动过程转轮的动应力。Funan Chen[20]通过准静态方法研究了水泵水轮机启动过程转轮的应力变化。

本文以某原型抽水蓄能机组为研究对象,对水轮机工况启动暂态过程机组流道内的压力脉动特性和转轮动应力特性进行了计算分析,研究了转轮应力的动态变化规律,有助于深入理解水泵水轮机机组启动过程复杂条件下的内部流动和转轮动应力特性。

1 研究对象

机组全流道三维模型如图1所示。在建模过程中,不仅考虑了蜗壳、固定导叶、活动导叶、转轮、尾水管等主要的流域,还考虑了转轮和顶盖之间的间隙流域。该流域能够有效提高计算叶轮进口处和出口处的流场流动特征的准确性,更能够有利于计算机组整体的性能参数,例如,水头和轴向水推力等。该机组的单位转速n11为89.16r/min;单位流量Q11为191.34L/s;转轮叶片数Zb为9;活动导叶个数Zh为20;固定导叶个数Zg为20。

图1 原型水泵水轮机流域示意图

2 网格划分及边界条件设置

2.1 网格划分

整体机组流道划分为以下几个部分:蜗壳、固定导叶、活动导叶、转轮、尾水管、间隙和均压管。对网格进行了无关性验证,具体内容可参考文献[21]。在本文中选择310 万的网格数量作为最终网格方案。其中,转轮采用四面体网格,蜗壳、尾水管、间隙、固定导叶、活动导叶及均压管采用六面体网格,如图2(a)所示,转轮结构域有限元网格如图2(b)所示。

图2 水泵水轮机网格离散化

2.2 边界条件设置

本研究的流动计算采用SSTk-ω湍流模型,它是标准k-ω模型的变形,使用混合函数将标准k-ε模型与k-ω模型结合起来。湍动能k和湍动能比耗散率ω的表达式如下:

式中,k为湍动能,m2/s2;u′i为速度的脉动分量,m/s;ε为耗散率;ω为比耗散率,s-1;μ为动力粘度,kg/(m·s);ρw为密度,kg/m3。

该湍流模型通过求解以下两个输运方程得到k及ω。

式中,k为湍动能;ω为比耗散率;ρw为流体密度;μt是湍流粘度;xk为坐标;p为压力;μ为动力粘度系数;uj(j=1,2,3)为流体的速度分量;μt为涡流粘度系数;F1为混合函数;σk=2.0;σω=2.0;σω1=2.0;σω2=1.168;β*=0.09;d是到下一个表面的距离;CDkω是交叉扩散项。

湍流动力粘性系数μt可表示为:

式中,常数a1=0.31。

在转轮的动应力计算中,弹性结构瞬态动力平衡方程如下:

式中,B为基于单元形函数的应变矩阵;D为弹性矩阵。

然后根据第四强度理论计算等效应力,也就是Von Mises 应力,如式(12)[22]所示:

式中,σx、σy、σz分别为x、y、z平面上的正应力;τxy、τyz、τzx分别为x、y、z平面上的切应力。

模拟的参考压力设置为1 个大气压,所有壁面均为无滑移壁面。对于抽水蓄能系统中的管路等部件,采用一维建模的计算形式得到三维模型机组的进出口边界条件,进出口压力随时间变化可参考文献[21]。

在动态网格模拟过程中,使用边界层平滑方法对边界层网格进行变形。在本算例中,在活动导叶和固定导叶表面上都存在边界层。因此,边界层区域中每个元素的节点坐标根据基准面区域中相应节点相同的位移矢量更新,以确保边界层网格的稳定性,活动导叶随时间变化的示意如图3所示。

图3 活动导叶随时间变化示意图

3 数值计算结果分析

3.1 机组外特性变化

图4 为机组性能参数随时间变化的曲线。在t=6～22s 内,导叶开度从1.5°转到5.6°,然后t=27s 时下降到3.8°;在t=6～26s 内,转速从50r/min 上升到额定转速375r/min,然后保持不变;转轮扭矩从2.3MN·m 先上升到4.0MN·m,然后在t=27s 时下降到0;流量受导叶开度的影响非常明显,处于先上升后下降趋势,从15m3/s 上升到32m3/s,然后下降到20m3/s 附近;水头在430～480m 左右波动。

图4 机组性能参数随时间变化的曲线

3.2 转轮内部压力分布变化

不同时刻转轮流固耦合面上的压力分布如图5所示,随着转速的增加,流固耦合面上的整体压力值显著增加。在t=6s 时,高压区在转轮进水边压力面的一侧,主要因为流量较小,水流冲击叶片压力面。随着时间的推移,转速逐渐上升,高压力值区域逐渐扩大,到t=26s 时,高压区在叶片进水边吸力面的一侧。将计算得到的转轮流固耦合面上的压力映射到转轮结构场中(图5(b)),开展水轮机工况启动过程转轮的动应力分析。

图5 转轮流固耦合面的压力分布

3.3 转轮应力分布变化

图6 为机组转轮进水边与下环、上冠交接处(分别命名为A点、B点)的动应力变化过程。可以发现,在t=6～11s 时,A点应力的均值约为32MPa,峰峰值为17MPa。在t=11～21s 时,应力呈现下降趋势,并达到最小值15MPa,这一时间段内的峰峰值也有所减小。在t=21s 之后,应力开始上升,达到43MPa,峰峰值也随之增加。总体看来,进口下环处的应力一直处于较低水平。

图6 转轮进水边的应力随时间变化曲线

在t=6～11s 时,B点应力在15MPa 附近,峰峰值为10MPa。在t=11～26s 时,应力呈现上升趋势,达到120MPa,其峰峰值为8MPa,B点应力与转轮转速的变化趋势基本保持一致。图7 为关键时间点(t=6s,11s,16s,21s,26s,31s,以绿色线段表示)的转轮应力分布图。在t=16s 之前,最大应力位置在转轮进口与下环的交接处(A点),在t=16s 之后,最大应力位置在转轮进口与上冠交接处(B点)。

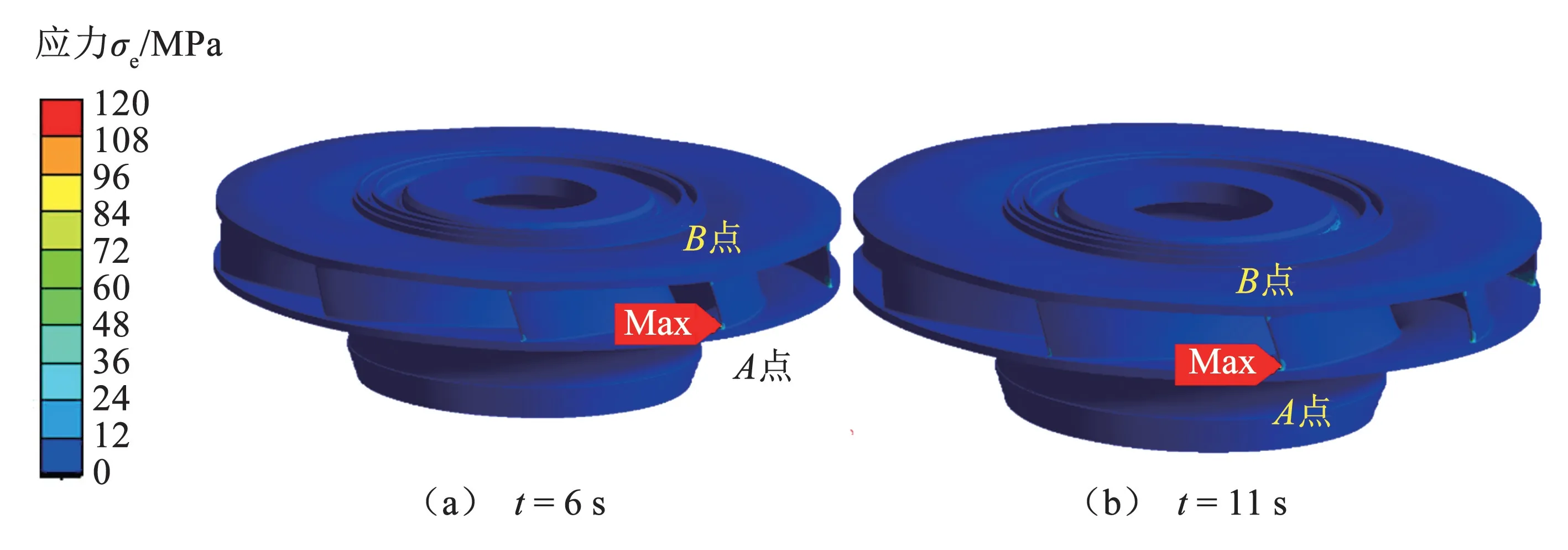
图7 转轮的应力分布

4 结论

本文针对某原型水泵水轮机组的水轮机工况启动过程进行了全流道内部流动和转轮流固耦合数值计算,重点分析水泵水轮机转轮内流场和动应力特性。主要结论如下:

(1)转轮扭矩呈先上升后下降的趋势,在转速达到额定值时,扭矩接近于0;流量受到导叶开度的影响非常明显,处于先上升后下降趋势;水头在430～480m 左右波动。

(2)随着转速的增加,转轮流固耦合面上的整体压力值显著增加。高压区起始集中在转轮进水边的压力面一侧,随着时间的推移,高压区域逐渐扩大并移动到进水边的吸力面一侧。

(3)转轮进水边与下环交接处的应力呈现先下降后上升的趋势,应力均值下降的同时,峰峰值也有所下降,其应力值一直处于较低的水平。转轮进水边与上冠交接处的应力呈现上升趋势,并与转轮转速的变化趋势基本一致。