关于树的biharmonic指数的研究*

郑学谦,乔晓云

(山西工程科技职业大学 基础课教学部,山西 榆次 030619)

设G是n阶简单连通图,其顶点集为V={v1,v2,…,vn},边集为E={e1,e2,…,em},顶点vi的度记作di(i=1,2,…,n),不妨设d1≥d2≥…≥dn,于是G的度序列可记为(d1,d2,…,dn).用A表示G的邻接矩阵,而G的度对角矩阵表示为D=diag(d1,d2,…,dn),则G的Laplace矩阵定义为L(G)=D-A,其特征多项式|λI-L(G)|称为G的Laplace特征多项式,其特征值称为G的Laplace特征值(记作λi,i=1,2,…,n,并约定0=λ1≤λ2≤…≤λn).本文涉及的其他概念可见文献[1].

1 相关引理

引理1[8]设a1,a2,…,an均为非负实数,则有

其中等式成立当且仅当a1=a2=…=an.

引理2[8](Pólya-Szeg不等式) 设ai,bi(1≤i≤n)均为正实数,则有

其中

M1=max{a1,…,an},M2=max{b1,…,bn},

m1=min{a1,…,an},m2=min{b1,…,bn}.

引理3[7]设Tn是n阶树,且d1+d2=n,则Tn的Laplace特征多项式为

φTn(λ)=λ(λ-1)n-4(λ3+(n+2)λ2+(n+2+d1d2)λ-n).

2 主要结果

证明由引理1得

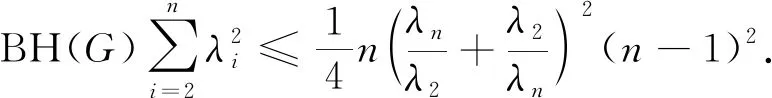
定理2设Tn是n阶树,且有d1+d2=n,则

证明由引理3得

φTn(λ)=λ(λ-1)n-4(λ3+(n+2)λ2+(n+2+d1d2)λ-n).

记

f(λ)∶=λ3+(n+2)λ2+(n+2+d1d2)λ-n.

设f(λ)的三个根为x1,x2,x3,则由韦达定理得

故

于是有

推论1设Hn是度序列为(n-2,2,1,…,1)的n阶树,则

证明由定理2得

推论2设Sn是度序列为(n-3,3,1,…,1)的n阶树,则

证明由定理2得

设K1,s是含有s+1个顶点的星图.

定理3设T(s,t)是用一条边连结不相交的星图K1,s和K1,t的中心所得到的n阶树,则

证明直接计算得φT(s,t)(λ)=λ(λ-1)n-4(λ3-(n+2)λ2+(2n+st+1)λ-n).记

f(λ)∶=λ3-(n+2)λ2+(2n+st+1)λ-n.

设f(λ)的三个根为x1,x2,x3,则由韦达定理得

故

从而