高一上学年期末专题复习与总结
2024-01-27卢智军张文伟
■卢智军 张文伟
数学必修第一册是进入高中阶段学习的基础知识,也是高一学习的重要知识,这部分的主要内容有集合与常用逻辑用语,一元二次函数,方程和不等式,函数的概念与性质,指数函数与对数函数,以及三角函数。下面就这部分知识进行复习与总结,希望对同学们的学习有所帮助。
1.集合中元素的互异性
解决集合相等问题时,易产生与互异性相矛盾的增解,这需要解题后进行检验。有些集合问题很难从整体着手解决,可以分类讨论进行求解。
例1 已知集合A={12,a2+4a,a-2},且-3∈A,则a=( )。
A.-1 B.-3或-1
C.3 D.-3
解:因为A={12,a2+4a,a-2},且-3∈A,所以a2+4a=-3或a-2=-3。
①当a2+4a=-3 时,即a2+4a+3=0,解得a=-1 或a=-3。若a=-1,则A={12,-3,-3},不满足互异性,舍去。若a=-3,则A={12,-3,-5},满足题意。
②当a-2=-3 时,解得a=-1,不符合题意。
综上可得a=-3。应选D。
跟踪训练1:已知集合A={x,x+1,1},B={x,x2+x,x2},且A=B,则( )。
A.x=1或x=-1
B.x=1
C.x=0或x=1或x=-1
D.x=-1
提示:当x=1 时,集合A={1,2,1},B={1,2,1},不满足集合元素的互异性,排除ABC。当x=-1时,A={-1,0,1},B={-1,0,1},这时A=B。应选D。
2.“补集思想”的应用
求补集时,要注意全集是否为实数集。利用数轴求解此类问题,要注意端点值能否取到,可以采用代入验证的方法确定端点值。
例2 已知全集U=R,集合A={x|x<3或x≥7},B={x|x A.{a|a>3} B.{a|a≥3} C.{a|a≥7} D.{a|a>7} 解:因为A={x|x<3 或x≥7},所以∁UA={x|3≤x<7}。又(∁UA)∩B≠∅,所以a>3。应选A。 跟踪训练2:已知集合A={x|x>a+3或x 提示:A={x|x>a+3 或x 图1 由包含关系确定集合中所含参数的值(取值范围)是集合间关系的重要应用,一般可借助数轴解决此类问题,且要注意空集的情况。 例3 已知集合A={x|-5≤x≤6},B={x|2m-1≤x≤m+1}。若A∪B=A,求实数m的取值范围。 解:因为A∪B=A,所以B⊆A。①当B=∅时,2m-1>m+1,即m>2,此时B⊆A成立;②当B≠∅时,由题意可得解得-2≤m≤2。综上可得,实数m的取值范围是{m|m≥-2}。 跟踪训练3:已知集合A={x|1 综上可得,a=0或a≥2或a≤-2。 解答这类问题的常用方法与步骤:化简p,q两命题;根据p与q的关系(充分、必要条件),转化为集合间的关系;根据集合间的关系,建立不等式组;求出参数的取值范围。 例4 是否存在实数p,使“4x+p<0”是“x2-x-2>0”的充分条件? 如果存在,求出p的取值范围。 跟踪训练4:已知集合A={x|-2 提示:因为x∈A是x∈B成立的充分不必要条件,所以(-2,6)是[2-m,2+m]的真子集,所以解得m≥4,即所求实数m的取值范围是[4,+∞)。 一般命题的否定通常是在条件成立的前提下否定其结论,得到真假性完全相反的两个命题;含有一个量词命题的否定,是在否定其结论的同时,改变量词的属性,即将全称量词改为存在量词,将存在量词改为全称量词。与一般命题的否定相同,含有一个量词命题的否定的关键也是对关键词的否定。 例5 (1)下列语句不是全称量词命题的是( )。 A.任何一个实数乘以零都等于零 B.自然数都是正整数 C.高一(1)班绝大多数同学是团员 D.每一个实数都有大小 (2)命 题p:“∀x∈R,x2>0”,则( )。 A.p是假命题;¬p:∃x∈R,x2<0 B.p是假命题;¬p:∃x∈R,x2≤0 C.p是真命题;¬p:∀x∈R,x2<0 D.p是真命题;¬p:∀x∈R,x2≤0 解:(1)A 中命题可改写为:任意一个实数乘以零都等于零,A 是全称量词命题。B中命题可改写为:任意的自然数都是正整数,B是全称量词命题。C 中命题可改写为:高一(1)班存在部分同学是团员,C 不是全称量词命题。D 中命题可改写为:任意的一个实数都有大小,D 是全称量词命题。应选C。 (2)由 于02>0 不 成 立,故“∀x∈R,x2>0”为假命题。根据全称量词命题的否定是存在量词命题可知,“∀x∈R,x2>0”的否定是“∃x∈R,x2≤0”。应选B。 跟踪训练5:命题“能被7整除的数是奇数”的否定是____。 提示:原命题即为“所有能被7整除的数都是奇数”,是全称量词命题。该命题的否定是:“存在一个能被7整除的数不是奇数”。 不等式的性质是进行不等关系推理运算的理论基础,要熟练掌握不等式的性质及应用条件,以防推理出错。 A.1个 B.2个 C.3个 D.4个 跟踪训练6:(多选题)下列命题正确的是( )。 一元二次不等式常与集合、方程等交汇命题,主要考查运算能力、逻辑推理能力,以及数学建模能力。对于不含参数的一元二次不等式,可转化为ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)的形式,结合二次函数的图像求解。对于含参数的一元二次不等式,应先看二次项系数的正负,再考虑判别式,最后根据两根的大小进行分类讨论。 跟踪训练7:已知a∈R,解关于x的不等式ax2-2x+a<0。 提示:当a=0时,原不等式为-2x<0,其解集为{x|x>0}。 当a<0 时,Δ=4-4a2,①当Δ>0,即 基本不等式是不等式部分的重要内容,其主要应用是求最值或取值范围。求最值问题,既适用于一个变量的情况,也适用于两个变量的情况。 例8 设x<-1,求的最大值。 函数的值域由函数的定义域和对应关系确定,一旦函数的定义域和对应关系确定了,值域也就确定了。求函数的值域没有统一的方法,如果函数的定义域是由有限的几个数构成的集合,那么可将函数值一一求出来,构成的集合即为值域;如果函数的定义域是一个无限数集,那么可根据函数解析式的特点,采取相应的方法求其值域。 例9 求下列函数的值域。 函数的性质包括函数的单调性、奇偶性、对称性和周期性,从高考命题形式上看,抽象函数、具体函数都有涉及,其中函数单调性的判断与证明、求单调区间、利用函数单调性求参数的取值范围是高考考查的重点。利用函数的奇偶性、对称性研究函数的图像是学习的难点。 (1)确定函数f(x)的解析式。 (2)用定义证明:f(x)在(-1,1)上是增函数。 (3)解不等式f(t-1)+f(t)<0。 跟踪训练10:设函数f(x)对任意的x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(1)=-2。 (1)求证:f(x)是奇函数。 (2)在区间[-3,3]上,f(x)是否有最值? 如果有,求出最值;如果没有,说明理由。 提示:(1)令x=y=0,则f(0+0)=f(0)+f(0),所以f(0)=0。 令y= -x,则0=f(0)=f(x)+f(-x),所以f(x)为奇函数。 (2)任取-3≤x1 函数y=ax及y=logax(a>0,且a≠1)的图像关于直线y=x对称,前者恒过(0,1)点,后者恒过(1,0)点,两函数的单调性均由底数a决定。在解题中要注意由翻拆、平移等变换得出的函数图像。利用函数的图像与性质比较大小,利用方程和不等式求解问题,都是高考的常考题型。 例11 已知a>0,a≠1,且loga3>loga2,若函数f(x)=logax在区间[a,3a]上的最大值与最小值之差为1。 (1)求a的值。 (2)若1≤x≤3,求函数y=(logax)2-loga x+2的值域。 解:(1)因为loga3>loga2,所以f(x)=logax在[a,3a]上为增函数。又f(x)在[a,3a]上的最大值与最小值之差为1,所以loga(3a)-logaa=1,即loga3=1,故a=3。 跟踪训练11:设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )。 A.奇函数,且在(0,1)上是增函数 B.奇函数,且在(0,1)上是减函数 C.偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数 提示:由题意得函数f(x)的定义域为(-1,1)。因为f(-x)=ln(1-x)-ln(1+x)=-f(x),所以f(x)为奇函数。因为,而-1在(0,1)上为增函数,所以f(x)在(0,1)上为增函数。应选A。 函数的零点就是相应方程的根,是相应函数图像与x轴交点的横坐标。因此,判断函数零点的个数可转化为求解方程的根或两函数图像的交点个数。零点存在定理是判断函数是否存在零点的一种方法,注意其使用条件:连续性和异号性。 例12 已知定义在R 上的函数f(x)的图像是一条不间断的曲线,满足f(a)≠f(b),其中a A.(0,1) B.(1,2) C.(2,3) D.(3,4) 利用三角恒等变换研究函数性质的方法与步骤:运用和、差、倍、半角公式化简;统一把f(x)化为f(x)=asinωx+bcosωx+k的形式;利用辅助角公式化为函数f(x)=Asin(ωx+φ)+k的形式,研究其性质。 (1)求f(x)的最小正周期和最大值。 (2)讨论f(x)在上的单调性。 (多选题)在△ABC中,下列等式一定成立的是( )。 B.sin(2A+2B)=-cos2C C.tan(A+B)=-tanC D.sin(A+B)=sinC
3.利用集合之间的关系求参数

4.利用充分条件与必要条件求参数的值或取值范围

5.全称量词命题与存在量词命题
6.不等式的性质及其应用

7.一元二次不等式的解法



8.利用基本不等式求最值
9.函数值域的求法

10.函数性质的应用
11.指数函数、对数函数的图像与性质
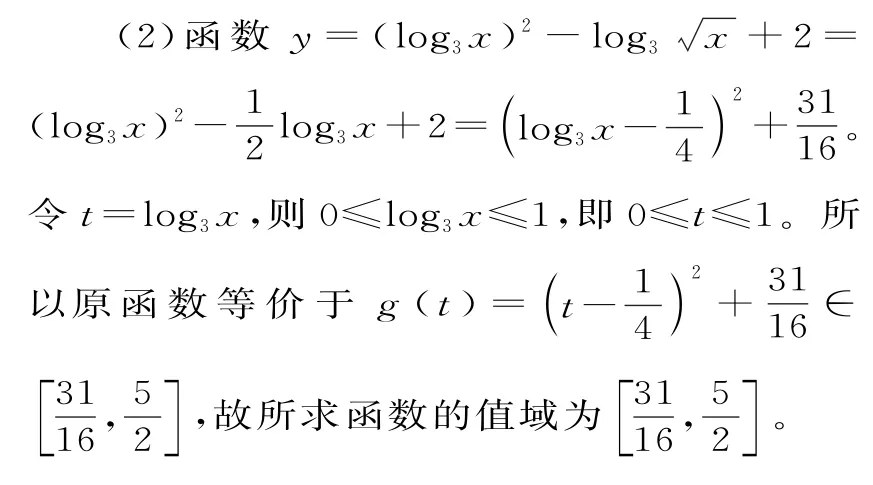
12.函数的零点与方程的根


13.三角恒等变换的综合应用

