强噪声下压力传感器触觉信号的提纯算法设计∗

张 燕，毛莉君

(西安培华学院智能科学与信息工程学院，陕西 西安 710125)

近年来，在智能制造领域中发展迅速，压力传感器被广泛应用在交通管制、运动健康、空间探索等行业领域[1]。随着科学技术的快速发展，人们对压力传感器触觉信号的提纯方法，提出了更高的要求，不仅要求信号提纯效率高，还要求其在复杂感知环境下依然具备精准的提纯能力[2]。在相关研究中，惠文珊等[3]提出了一种基于卷积神经网络(CNN)和长短期记忆(LSTM)神经网络的融合模型，对压力触觉信号序列识别。该方法可以准确识别不同类型的压力触觉数据，但是由于传感器触觉信号存在不同程度的噪声，导致信号识别的时间较长。张秀丽等[4]对可穿戴式触觉压力传感设备单元，静态标定，利用D－H 法建立了触觉传感单元的运动学模型，实现了触觉正压力方向信号的分析。该方法可以准确标定触觉设备信号，但信号提纯的精准度有待进一步完善。Tanaka 等[5]研究了抓取操作中，人机协作的双边共享触觉感知方法。其设计了一个双边共享的触觉系统，用于抓取操作。该方法根据人类的触觉信息控制抓握力，通过手指连接的压力传感器提取信号。该方法提高了触觉信号提纯的稳定性，但对信号噪声的处理仍需进一步优化。

为了解决上述方法中存在的问题，本文设计了基于局域波分解的强噪声下压力传感器触觉信号提纯方法。

1 提纯算法的设计与实现

压力传感器存在内部导电微粒不连续的情况，当外加反向电压时，耗尽区的变化相反，从而产生了较强的噪声。强噪声影响下，压力传感器的触觉信号存在噪声、信号泄漏及回波重叠等情况，从而提高信号提纯的准确性与效率。因此算法需要对传感信号降噪与校正。本文利用局域波分解方法，消除强噪声下的信号冗余信息，设计校正法信号，完成信号提纯。

1.1 传感信号局部均值特征的计算

利用局域波分解计算强噪声下，压力传感器触觉信号的局部均值特征，可以消除信号中的冗余信息，具体步骤如下:

①局域波分解的原理是将某个时刻压力传感器的多个瞬间频域分解[6]到不同的基本模式分量中，即将原时间序列信号经过局域波分解后得到不同的基本模式分量，公式如下所示:

式中:u描述的是时间序列；t代表的是时刻；s表示的是趋势项；d表示的是第i个基本模式分量；n为分量总个数。

②强噪声下压力传感器中的触觉信号经过局域波分解后，得到若干个局域波分量。对于具备相同时间序列的触觉信号，计算极大值点与极小值点，分别用umax(t)和umin(t)表示。然后采用插值法[7]计算出极大值点与极小值点构成的信号包络范围，分别用fmax(t)和fmin(t)表示。

③根据信号的包络范围，计算出强噪声下，压力传感器触觉信号的局部均值，公式如下所示:

式中:o(t)描述的是局部均值。

④为了确定局部均值中是否含有噪声成分，计算强噪声下压力传感器触觉信号的分解分量，利用如下公式计算出所有分解分量与原始信号的关系。

式中:j表示分解分量；R为分解分量与原始信号的关系值。η表示的是白噪声集合；F表示原始信号集合。

⑤如果分解分量与原始信号的关系值较小，则说明这个分量中含有噪声成分。利用式(4)对此分量对称分解[8]，完成压力传感器触觉信号的降噪处理，保证局部均值的准确性。

式中:k表示的是对称分解次数。在完成触觉信号降噪的基础上，为了提高强噪声下信号提纯的精准度，需要对信号进行校正处理。

1.2 压力传感信号的频谱特征分析

在强噪声下压力传感器触觉信号的提纯过程中存在信号泄露、背景回波重叠等问题的干扰[9]。因此设计一种压力传感器触觉信号校正法，对传感信号的局部均值实施校正处理，具体步骤如下:

①背景直流和幅相失衡是导致压力传感信号偏移的主要因素，强噪声下压力传感器的触觉信号会经过缩放、移动和旋转等操作，校正处理就是对信号做出反变换处理，公式如下所示:

式中:B代表的是测量信号；e为直流分量；i表示信号个数，ϑ表示相位不平衡系数；L为幅相失衡系数，和局部均值相关。

②校正之后的压力传感器触觉信号，重新回归正交状态，此时需要获取幅度失衡系数以及相位失衡系数。将混频器输入值设为压力传感器稳定时的测试信号，对输出的中频信号进行分析，得到幅度失衡系数以及相位失衡系数。利用距离函数表达相位失衡系数，完成强噪声下压力传感器待测信号的多目标测距，公式如下所示:

式中:μ为距离函数的一般系数；f表示的是距离函数；WJ、WR分别表示正交输出。

③在强噪声下压力传感器中引入等效的中频信号后，将误差系数与正交输出相结合，得到复合信号。复合信号经过牛顿欧拉变化[10]后得到频域特征W(e)，公式如下所示:

④强噪声下压力传感器触觉信号的频域特征由三部分组成，分别是主频域、副频域和直流分量。如图1 所示。

图1 频谱特征

频域特征的幅值包括压力传感器的误差系数，所以可以从误差系数中计算出直流量、幅相失衡系数与实际波长，完成强噪声下压力传感器触觉信号的校正，公式如下所示:

式中:S为复合信号的真实值；M表示的是采样点数量；I代表复合信号的虚假值。

1.3 压力传感器触觉信号提纯

在上述信号降噪与校正的基础上，提纯传感器触觉信号。小波变换法可以覆盖整个频域，极大地减小或去除所提取的不同特征之间的相关性，本文根据小波在时域和频域都具备局部特征变化的性能。利用小波变换法来提纯强噪声下压力触觉信号，具体过程如下:

①小波变换法具有分析信号的能力，即在强噪声下压力传感器信号的时频具有表达触觉信号的能力，用式(9)表示连续小波变换式的函数[11]形式:

式中:X表示的是小波变换式；x表示的是尺度因子；y表示的是平移因子；g(c)表示函数。c为触觉信号。

②不同于其他的信号提纯方法，小波变换对强噪声下压力传感器触觉信号的提纯过程，可以采用小波基函数。最佳小波基可以使强噪声下压力传感器中的触觉信号，在时间平面中的系数最大化，同时保证信号取得局部极大值。

③此时的小波基函数可以提纯出强噪声下压力传感器中所有触觉信号的频率成分[12]。然后通过改变尺度因子[13]与平移因子的大小调整频率分辨率和时间分辨率，公式如下所示:

式中:Z表示传感器信号的频域；a表示的是信号双指数。

④利用阈值重构频率成分。强噪声下压力传感器的触觉信号主要集中在小波分层上[14]，且触觉信号分布范围较广。因此在重构触觉信号波形前，先去除含有较少局部能量的信号，这样可以在损失较少量信号的情况下，消除重构波形中的边缘信息。利用式(11)选取小波重构波形对应的各层分量的阈值:

式中:ν为阈值；q表示的是中值数；p为系数总数量；j表示尺度。

⑤引入软阈值[15]获取最佳触觉信号区间，软阈值的作用是将阈值与强噪声下压力传感器触觉信号的绝对值相比较，如图2 所示。

图2 软阈值处理法

当信号的绝对值小于等于阈值时，将信号值变为零。当绝对值小于阈值时，将此信号点变为与阈值之间的差值，公式如下所示:

至此，完成了强噪声下压力传感器触觉信号的提纯。

2 实验分析

2.1 提纯实验研究

为了验证本文设计的强噪声下压力传感器触觉信号提纯方法的整体有效性，进行实验测试。实验环境如图3 所示。

图3 实验环境分析

本文的基线算法有局域波分解、校正算法和小波变换法。首先，局域波分解强噪声下原始压力传感器的触觉信号F，以降低提纯干扰。其次，利用校正算法计算M个采样点的直流分量、幅相失衡系数与实际波长，提取到触觉信号的频谱特征。最后利用小波变换法，在频域信号频域Z6 Hz～8 Hz 的范围下，调整尺度因子x和平移因子y。利用软阈值将信号点变为与阈值之间的差值。设置传感器信号频域Z的范围为6 Hz～8 Hz，设相位不平衡系数ϑ为0.5。本文参考了文献[12]的传感信号的采集方式，为分配夹取任务，设置夹具速度为50 mm/s，将压力传感单元触觉信号的检测阈值ν设置为0.1 N。

通过图4 的统计结果可以看出，本文的方法可以很好地在原始干扰信号中，提纯压力信号，排除大部分干扰。

图4 提纯实验结果

2.2 实验结果统计

利用不同方法提纯执行夹取任务时的信号，分别对比信号提纯时间、信噪比、均方根误差等实验指标。采用基于小波变换的强噪声下压力传感器触觉信号提纯方法、文献[3]方法、文献[4]方法和文献[5]方法做出对比测试。

2.2.1 信号提纯时间

采用所提方法、文献[3]方法、文献[4]方法和文献[5]方法提纯10 组强噪声下压力传感器触觉信号，对比不同方法所用的提纯时间。提纯时间越长，算法的提纯效率越低，相反，提纯时间越短，算法的效率越高，不同方法的测试结果如图5 所示。

图5 不同方法的信号提纯时间

分析图5 中的数据可知，针对强噪声下压力传感器触觉信号的提纯，所提方法的提纯时间在2 s上下波动。文献[3]方法、文献[4]方法和文献[5]方法的提纯时间分别在5 s 至8 s 上下波动。通过对比发现，在不同仿真次数下所提算法的提纯时间均低于文献[3]方法、文献[4]方法和文献[5]方法的提纯时间，表明所提算法触觉信号的效率高于对比方法的效率。

2.2.2 信噪比

信噪比是评价算法抗噪声能力的重要指标，信噪比数值越大，表明算法的抗噪声能力越强；信噪比数值越小，表明算法的抗噪声能力越弱。其计算公式如下:

式中:SNR 代表的是信噪比数值；y代表的是原始信号。l为剩余噪声；y′为经过去噪后的信号；var 表示方差。为保证测试结果的公正性，本次测试在15 组强噪声下压力传感器环境下完成，将所提方法、文献[3]方法、文献[4]方法和文献[5]方法的信噪比测试结果绘制成表，方便分析，如图6 所示。

图6 不同方法的信噪比

分析图6 可知，无论是哪组仿真测试中，所提算法的平均信噪比为14.13 dB，高于文献[3]方法、文献[4]方法和文献[5]方法的信噪比数值，说明所提方法的抗噪声能力强于对比的三种方法的抗噪声能力。并且随着仿真次数的增加，所提方法的信噪比数值比较稳定，没有发生明显浮动。而用于对比的三种方法的信噪比数值上下浮动较大。表明针对强噪声下压力传感器触觉信号的提纯，所提方法抗噪能力的稳定性较强。所提方法在对强噪声压力传感器触觉信号提纯之前，利用局域波分解对信号完成了去噪处理，进而在提纯过程中不受噪声的影响，表明所提方法具有良好的抗噪声能力。

2.2.3 均方根误差

均方根误差表示的是算法提纯的强噪声下压力传感器触觉信号与原始信号的平均偏离程度，是衡量算法精准度的重要指标。均方根误差数值越大，表明算法提纯的信号与原始信号偏离程度越大，即精准度越低。均方根误差数值越小，表明提纯信号与原始信号之间的偏离程度越小，即精准度越高。其计算公式如下所示:

式中:MSE 代表的是均方根误差。

所提方法、文献[3]方法、文献[4]方法和文献[5]方法的测试结果如图7 所示。

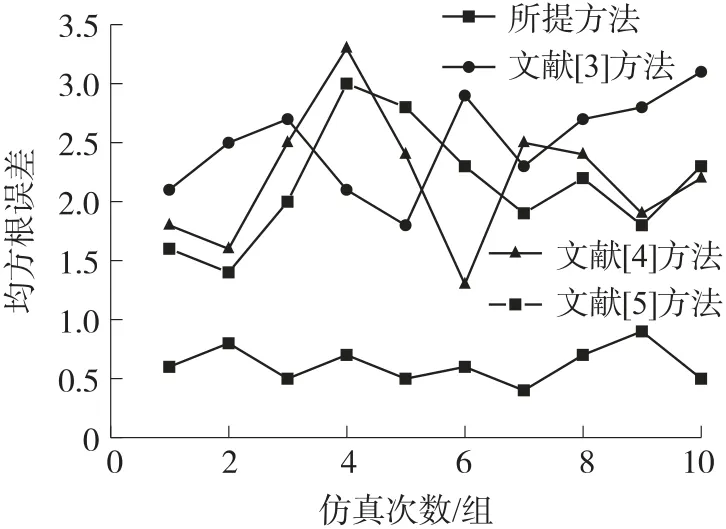
图7 不同算法的均方根误差

对图7 分析可知，无论是哪组仿真测试中，所提方法的平均均方根误差为0.63，均低于文献[3]方法、文献[4]方法和文献[5]方法的均方根误差。说明针对强噪声下压力传感器触觉信号的提纯，所提方法提纯结果与目标信号之间的偏离程度较小，即所提方法的提纯精准度高于对比的三种方法的提纯精准度。并且随着仿真次数的增加，所提方法的均方根误差比较稳定，没有发生大幅度波动，而文献[3]方法、文献[4]方法和文献[5]方法的均方根误差不稳定，上下波动较大，说明所提方法的提纯精准度稳定性强于对比的三种方法提纯精准度的稳定性。

4 结束语

本文提出了基于小波变换的强噪声下压力传感器触觉信号提纯算法。

①该方法首先对压力传感器中的触觉信号实行降噪处理，其次采用雷达微波方法校正信号，最后采用小波变换法分解和重构信号，完成强噪声下压力传感器触觉信号的提纯。

②经验证，该方法的提纯时间在2 s 上下波动，平均信噪比为14.13 dB，平均均均方根误差为0.63。方法在提高了信噪比的同时，降低了方法的提纯时间和均方误差。