基于IFWA-ELM 的六维力传感器解耦算法∗

董 翔，许子健，曹会彬，孙玉香，高理富

(1.安徽大学电气工程与自动化学院，安徽 合肥 230601；2.中国科学院合肥物质科学研究院，安徽 合肥 230031；3.中国科学技术大学信息科学技术学院，安徽 合肥 230027)

六维力传感器是机器人实现智能化控制的核心器件之一，在机器人领域占有非常重要的地位[1]。目前，基于电阻应变式[2]测量原理的六维力传感器被广泛应用，其采用电阻应变片感应外力变化，通过惠斯通桥路转换为电压输出，具有测量精度高，静态性能稳定等优点。然而六维力传感器的各维度间存在耦合，严重影响传感器的测量精度[3]。

六维力传感器的解耦方法包括结构解耦和软件解耦。结构解耦是从结构设计、加工工艺等方面减小耦合，但是这种方法操作难度大，不易实现，且成本较高。2017 年，Niu 等[4]设计了一种基于过约束并联机构的新型传感器结构，用于大量程力测量，实验结果表明，通过该方法获得的预测力/力矩与实际加载的力/力矩基本一致，最大耦合误差为1.98%。2021 年，Xiong 等[5]设计了一种多层感知的弹性体结构，通过差分测量的方法感知力/力矩的应变，降低了六维力传感器的耦合干扰。2022 年，Nasab等[6]设计了一种非对称结构的三维力传感器，传感器的每一维都独立地在力和位移之间建立一种由硅结构覆盖的关系，实验结果表明，非对称结构有效降低了三维力之间的耦合。软件解耦采用软件算法实现解耦，具有成本低、灵活性高等优点。软件解耦可以分为两种，一种是线性解耦，另一种是非线性解耦。线性解耦是利用最小二乘法(LS)确定输入输出的关系，然而六维力传感器的输入和输出关系通常是非线性的，因此基于最小二乘法的线性解耦很难取得较好的解耦效果。常用的非线性解耦方法包括:BP 神经网络(BPNN)、极限学习机(ELM)、支持向量回归(SVR)等[7]。BP 神经网络是一种采用误差反向传播算法训练的多层前馈神经网络，由于其简单有效，BP 神经网络是一种应用广泛的非线性解耦方法，然而这种基于梯度下降的迭代学习算法训练时间长，且易陷入局部最优解。2020 年，张弘昌[8]采用遗传算法对BP 神经网络的初始权值和阈值进行优化，有效降低了多维力传感器的耦合误差。2022 年，Li 等[9]提出了一种基于全局最优适应度函数的BP 神经网络算法(GOFF-BP)，来解决三维力之间的解耦问题，解耦算法能在短时间内找到最优解，解耦后Ⅰ类误差和Ⅱ类误差均控制在1.5%以内。2021 年，Liu 等[10]提出了两种自适应偏置径向基函数神经网络(RBFNN)，具有用于多维力解耦的局部偏置和全局偏置方法，该方法可以提高RBFNN对具有显著偏差的动力学的逼近精度，从而提高控制性能。极限学习机是一种单隐含层前馈神经网络，通过随机生成网络权值和阈值的操作减少了训练时间，同时具有较高的预测精度。2018 年，梁桥康等[11]采用最小二乘法、BP 神经网络和极限学习机分别对五维力/力矩传感器进行解耦，实验结果表明，基于极限学习机的解耦方法能在保持效率的前提下获得较高的解耦精度。

虽然极限学习机具有训练速度快、泛化性能好等优点，但随机生成权值和阈值导致网络稳定性较差，容易陷入局部最优解，同时隐含层神经元数量难以确定，影响网络的预测精度。因此，许多学者对极限学习机进行优化，主要优化方法是将智能优化算法应用于极限学习机。2021 年，郑小霞等[12]提出了基于变分模态分解(VMD)和灰狼算法优化极限学习机(GWO-ELM)的轴承故障诊断方法，实验结果表明，GWO-ELM 模型能够有效识别故障类型，同时具有较高的故障识别率。2022 年，钟琳等[13]采用粒子群算法(PSO)对极限学习机进行优化，构建PSO-ELM 预测模型，应用于中国石油股票价格预测。2022 年，卢雪琴等[14]提出了一种基于鲸鱼算法优化极限学习机的微电网故障诊断方法，仿真结果表明，与BP 神经网络、RBF 神经网络和极限学习机相比，基于鲸鱼优化算法优化极限学习机的故障诊断模型具有更强的泛化性能和更高的识别精度。

烟花算法是一种基于烟花爆炸产生火花现象的群智能优化算法，由谭营等[15]于2010 年提出。烟花算法具有出色的全局搜索和局部搜索能力，是一种求解全局空间最优解的有效方法，烟花算法在交通、云计算、纺纱等领域具有广泛应用[16－18]。本文采用改进烟花算法(IFWA)对极限学习机进行优化，获得网络的最佳初始权值和阈值，并基于此提出了改进烟花算法优化极限学习机(IFWA-ELM)的解耦算法。同时，本文以应用于4 500 m 深海机械臂的六维力传感器作为研究对象，进行了标定实验和解耦实验。实验结果表明，IFWA-ELM 解耦算法具有较好的非线性解耦能力。

1 IFWA-ELM 算法

1.1 极限学习机

极限学习机随机生成输入层与隐含层之间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元数量，便可以得到唯一最优解。网络结构如图1 所示。

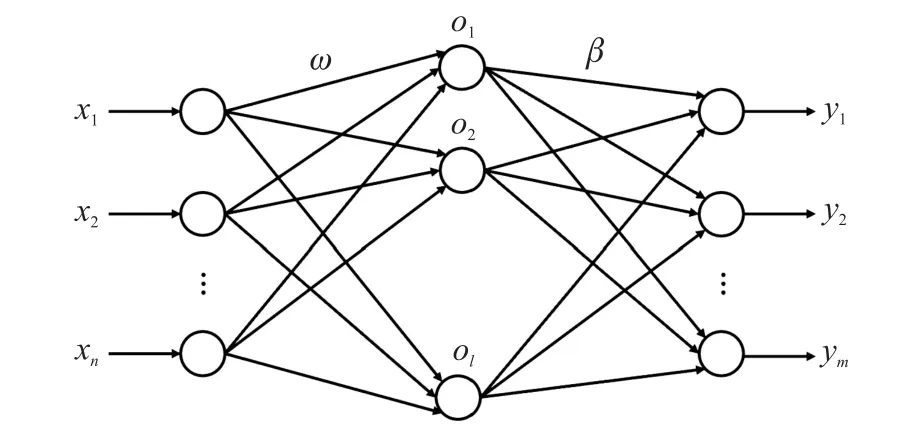
图1 ELM 网络结构图

假设有N个训练样本(Xi，Yi)，其中1≤i≤N，Xi＝[xi1，xi2，…，xin]T∈Rn为第i个样本的输入向量，Yi＝[yi1，yi2，…，yim]T∈Rm为第i个样本的输出向量，则ELM 网络可以表示为:

式中:g(x)为激活函数；Wf＝[wf1，wf2，…，wfn]T为输入权值；bf是第f个隐含层神经元的阈值；βf＝[βf1，βf2，…，βfm]为输出权值；Ti＝[ti1，ti2，…tim]T为第i个样本的输出向量。

ELM 的学习目标是使网络的输出误差尽可能最小，表示为:

即存在一组合适的W，b和β，使得:

式中:H＋为隐含层输出矩阵H的广义逆矩阵。

1.2 烟花算法

烟花算法主要包括3 个部分:爆炸算子、变异算子和选择策略。

爆炸算子的核心思想是适应度值较优的烟花在小范围产生大量火花，适应度值较差的烟花在大范围产生少量火花。根据适应度函数f(x)计算烟花适应度值，并据此计算烟花的爆炸半径Ri和爆炸火花数量Ni。

式中:r和n是常数，用来限制爆炸半径和爆炸火花数量；ε是一个极小的非零常数，用来避免分母为零；f(xi)表示烟花xi的适应度值；fmin和fmax分别表示最优和最差烟花的适应度值。

烟花爆炸通过位移在k维搜索空间内产生火花，位移操作公式如下:

式中:表示第i个烟花在第k维上的位置；rand(0，Ri)表示在爆炸半径Ri内生成的均匀随机数。

为了增加爆炸火花的多样性，随机选取部分火花进行变异操作，公式如下:

式中:g是均值为1、方差为1 的高斯分布随机数。

烟花算法采用基于距离的选择策略。首先保留最优个体进入下一代，再选择其他N－1 个个体。在候选集合K中，与其他个体距离较远的个体更有可能被选中。

式中:d(xi，xj)表示个体xi和个体xj之间的欧氏距离；R(xi)表示个体xi与其他个体的距离之和，K表示候选集合的火花总数。

采用轮盘赌的方式进行选择，每个个体被选择的概率为:

1.3 改进烟花算法

1.3.1 自适应爆炸半径

在原始烟花算法中，适应度值最优的烟花产生最多火花。然而最优烟花通过式(6)计算得到的爆炸半径非常小，接近于0，因此没有发挥挖掘作用。本文对最优烟花的爆炸半径进行改进，引入自适应方法[19]。烟花算法总是选取最优个体作为下一代烟花。自适应方法是利用这一代获得的信息去计算最优烟花在下一代的爆炸半径。在爆炸和变异产生的火花中，选择一个个体，以其与最优个体的距离，作为最优烟花在下一代的爆炸半径[13]。选取个体满足条件:

①适应度值大于这一代的烟花X。

②在满足条件①的所有个体中，与最优个体的距离最短。

式中:表示选择的个体；x∗表示所有烟花和火花中适应度值最优个体；d是一种距离度量，这里采用所有维度中最大的差值。

条件①要求所选个体与最优个体的适应度值之差大于烟花与最优个体的适应度值之差，即

这个不等式确保评价函数在范围d(，x∗)对应值域上的距离至少比这一代取得的进步更大。通过d(，x∗)来估计距离d(，x∗)，从而在下一代爆炸中找到一个更好的位置～，满足:

条件②用于确保半径收敛。为了减慢算法收敛速度，将计算得到的自适应半径乘以一个特定的系数λ，经过多次实验，取λ＝1.3。同时，为了避免半径剧烈波动，引入平滑机制，使用计算得出的自适应半径和这一代爆炸半径的平均值作为最优烟花在下一代的爆炸半径。

烟花种群初始化后，将最优烟花的爆炸半径设置为整个搜索空间的范围。对于之后的每一代，采用自适应方法计算最优烟花在下一代的爆炸半径。其他烟花的爆炸半径仍根据式(6)计算。

1.3.2 新型高斯变异算子

在原始烟花算法中，当随机产生的高斯分布随机数接近0 时，变异火花的位置会接近0，而且迭代后期很难跳出。本文采用新型高斯变异算子，使得变异火花沿着当前位置和种群中最优个体位置组成的直线方向上进行变异。

式中:e是均值为0、方差为1 的高斯分布随机数，xbk为当前种群中适应度值最优个体在第k维上的位置信息。

1.3.3 精英选择策略

原始烟花算法的选择策略需要构建任意两个个体之间的欧氏距离，这种策略虽然增加了下一代种群的多样性，但也增加了算法训练时间。烟花算法通过适应度值对个体质量进行评价，即适应度值越小，个体质量越高。为了减少算法训练时间，采用精英选择策略。首先适应度值最小的个体直接保留到下一代，然后采用轮盘赌的方法在候选集中选择剩余的N－1 个烟花，烟花被选择的概率公式如下:

易知，适应度值越低的个体被选择的概率越大，反之越小。这样使下一代更容易得到优质的烟花，提高了寻优效率。同时，适应度值最差的烟花也有概率被选择进入下一代，提高了种群的多样性，避免算法在迭代过程中过早收敛。

1.4 改进烟花算法优化极限学习机

改进烟花算法优化极限学习机是用改进烟花算法来优化极限学习机的初始权值和阈值，寻找最佳网络参数。输入层的权值和隐含层阈值作为烟花种群的参数，种群的维度大小为n＝h(d＋1)，h为输入层神经元个数，d为隐含层神经元个数。通过改进烟花算法得到最佳初始权值和阈值，代入网络进行训练。优化后的极限学习机能够有效降低随机生成权值和阈值对网络性能的影响，提高模型预测的准确性和稳定性。设置适应度函数为:

式中:yi为真实值，为预测值，n为样本数量。IFWA-ELM 算法流程如图2 所示，具体流程如下:

图2 IFWA-ELM 算法流程图

①初始化种群，随机生成N个烟花，设定初始迭代次数t＝1，最大迭代次数为T；

②计算每个烟花的适应度值，计算爆炸半径和爆炸火花数量进行爆炸操作，随机选择部分火花进行变异操作；

③根据选择策略在当前种群选择出N个个体作为下一代烟花种群；

④令t＝t＋1，判断迭代终止条件t>T是否成立，如果成立则终止迭代，否则继续执行步骤②；

⑤将最优烟花个体对应的参数作为极限学习机的最佳初始权值和阈值，构建IFWA-ELM 网络模型。

2 标定实验

2.1 标定实验的目的

标定是指利用标准的计量设备对待检测的设备进行校准的过程，六维力传感器的精确标定对测量性能至关重要。通过对六维力传感器的标定，可以获得传感器在不同受力状态下，输入力/力矩与输出电压的关系。同时，获得的大量力/力矩值与电压值为解耦实验提供训练样本和测试样本。本文以应用于4 500 m 深海机械臂的六维力传感器作为研究对象，传感器的实物如图3 所示。传感器的参数如表1所示。

表1 六维力传感器参数

图3 六维力传感器

2.2 标定实验的流程

六维力传感器的常用标定方法是用已知标准力源在不同方向对传感器加载标准力/力矩，加载的力/力矩从最小测量范围到最大测量范围呈恒定变化，同时在各加载点检测并记录传感器的输出电压。重复这个过程三次，得到完整的标定数据。标定平台量程如下:Fx/Fy为1 000 N，Fz为2 000 N，Mx/My/Mz为50 Nm，精度为0.1%F.S.。从六维力传感器标定平台，到给传感器施加载荷的标准砝码，再到力加载过程中的方向偏差，都会产生加载误差，从而影响传感器的精度[20]。例如，定滑轮轴承处存在摩擦力会产生附加力矩作用，进而产生误差。通常情况下，标定平台自身精度指标高于传感器一个等级。六维力传感器的标定平台和原理图如图4、图5 所示。具体标定流程如下:

图4 六维力传感器标定平台

图5 标定平台原理图

①跟据六维力传感器在各方向的量程范围，在各方向划分若干加载点；

②调整标定平台，将传感器用螺栓固定在标定平台上，并在其顶部安装加载帽；

③对六维力传感器各方向输出电压进行零基线校准；

④在Fx正方向上按划分的加载点逐步增加载荷至满量程，然后逐步减少载荷至零，重复3 次，记录输出电压；

⑤按照步骤④方法进行Fx负方向加载和卸载，并记录数据；

⑥按照步骤④、⑤方法对其他方向进行标定，完成各方向的标定，得到完整标定实验数据。

2.3 标定实验的结果

标定结果如图6 所示，根据标定曲线图可知，当某一方向施加载荷时，其他方向的输出电压都会产生或多或少的影响。因此，六维力传感器的各个方向之间存在一定的耦合。产生耦合的原因可以分为两种:结构性耦合和误差性耦合。结构性耦合产生的原因主要是因为弹性体的一体化结构，某些方向之间必然存在耦合，例如Mx方向与Fy方向、My方向与Fx方向之间。误差性耦合产生的主要原因是贴片水平的限制，在手工粘贴应变片的过程中，应变片实际粘贴位置与期望粘贴位置难免存在一定偏差。六维力传感器的维间耦合严重影响传感器的测量精度，因此需要对六维力传感器进行解耦。

图6 标定结果

3 解耦实验

3.1 解耦实验方案

首先对标定数据进行训练集和测试集的划分，采用留出法进行训练集与测试集的划分，标定数据的80%用于训练IFWA-ELM 算法，20%用于测试算法的解耦精度，训练集和测试集数据均包括全区间各方向不同加载情况下输出电压与加载力/力矩数据。在所处理的解耦样本中，最大力值为1 010 N，而力矩值的大小在±62 N•m 以内，数值的大小存在显著差异。为了消除不同量纲对数据分析的影响，同时提高网络的训练效率，需对数据进行归一化处理，归一化公式如下:

式中:min 和max 分别表示数据中的最小值和最大值；old＿value 表示归一化前的数据；new＿value 表示归一化后的数据。数据归一化处理后，映射到[－1，1]区间。然后构建IFWA-ELM 解耦模型，网络的输入层为传感器的输出电压，节点数为6，输出层为加载的力或力矩，节点数为6，隐含层激活函数为sigmoid。改进烟花算法的参数设置为:烟花种群大小N＝5，变异火花数量M＝5，爆炸半径调节常数r＝1，爆炸火花数量调节常数n＝50，爆炸火花数量上限值UN＝10，爆炸火花数量下限值LN＝2，最大迭代次数T＝500。

3.2 隐含层神经元数量分析

隐含层神经元数量对极限学习机的预测性能有较大影响。为了确定IFWA-ELM 算法的隐含层神经元数量的最优取值，以均方误差(MSE)作为指标来分析隐含层神经元数量对算法预测精度的影响，均方误差的计算公式如下:

式中:yi为第i个样本的真实值，为第i个样本的预测值，n为样本数量。

同时，为了验证IFWA-ELM 算法的预测性能，分别使用相同的数据样本对ELM、PSO-ELM、FWAELM 进行训练。PSO 算法的参数设置如下:c1＝c2＝1.494 45，种群大小为5，个体最大值popmax＝5，个体最小值popmin＝－5，个体速度最大值Vmax＝1.25，个体速度最小值Vmin＝－1.25，最大迭代次数maxgen ＝500。对于FWA 算法的参数选取采用与3.1 节中IFWA 算法相同的参数。

如图7 所示，原始ELM 算法的预测精度较差，当隐含层神经元为30，均方误差达到99.5。使用智能优化算法优化后的ELM 算法提高了预测精度。在不同隐含层神经元数量下，IFWA-ELM 算法的均方误差均低于PSO-ELM 和FWA-ELM。当隐含层神经元数量逐渐增加到90 时，IFWA-ELM 和ELM 的均方误差均先减小后趋于稳定。可见，增加隐含层神经元数量有利于提高解耦精度。IFWA-ELM 算法在均方误差最小时的隐含层神经元数量为75，而ELM 算法在均方误差最小时的隐含层神经元数量为80。当均方误差最小时，IFWA-ELM 比ELM 少了5 个隐含层神经元，同时IFWA-ELM 的最小均方误差比ELM 降低了66.327%。对比ELM，IFWA-ELM能以更少的隐含层神经元数量得到更高的解耦精度。

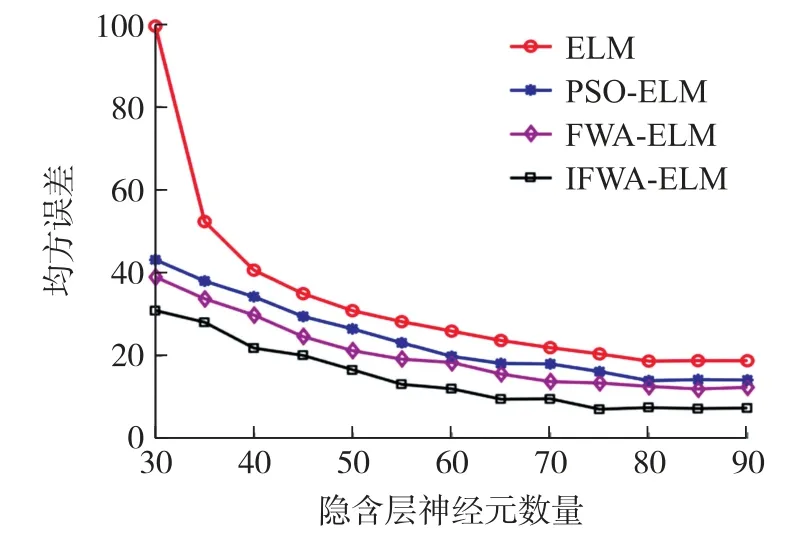
图7 隐含层神经元数量的影响对比

3.3 测量精度评价指标

六维力传感器在进行解耦之后，需要对传感器的测量精度进行评价。与单维力传感器不同，六维力传感器的误差除了各方向加载误差外，还存在各方向之间的耦合误差。采用Ⅰ类误差和Ⅱ类误差作为六维力传感器的测量精度评价指标。Ⅰ类误差反应主方向测量值与实际加载值之间的偏离程度，也称主方向上的非线性误差。其中，i方向的Ⅰ类误差用下式表示:

式中:Fi(P)表示i方向测得力/力矩；Fi(L)表示i方向实际施加力/力矩；Fi(FS)表示i方向的全量程值。

Ⅱ类误差表示某一方向施加载荷导致其他方向产生附加的干扰力/力矩，也称耦合误差。其中，j方向施加载荷对i方向产生的耦合误差用下式表示:

式中:Fij表示i方向施加力/力矩为零时，j方向施加力/力矩，在i方向所测得力/力矩；Fi(FS)表示i方向的全量程值。

3.4 解耦实验结果

为了验证IFWA-ELM 算法的解耦性能，选取LS、BPNN 和ELM 进行对比分析。BPNN 算法的参数如下:隐含层数设置为1，隐含层和输出层的激活函数分别设置为tansig 和purelin，选取trainlm 作为网络的训练函数，通过多次实验分析，隐含层神经元数量设置为60，学习速率为0.01，最大迭代次数为1 000，训练最小误差为1e－04。通过3.2 节的分析确定ELM 算法的隐含层神经元数量为80，IFWAELM 算法的隐含层神经元数量为75。

根据和Ⅰ类误差和Ⅱ类误差的定义，对六维力传感器解耦后的测量精度进行分析。六维力传感器使用不同算法解耦后的Ⅰ类误差和Ⅱ类误差如表2所示。从表2 可看出，传统线性解耦算法LS 的解耦性能较差，解耦后各方向的最大Ⅰ类误差为2.69%。BPNN 和ELM 各方向的最大Ⅰ类误差分别为0.53%和0.312%，Ⅰ类误差大幅降低。IFWA-ELM 算法的Ⅰ类误差被控制在0.27%以内，且6 个方向的Ⅰ类误差均小于其他算法，IFWA-ELM 算法能够有效降低各方向的非线性误差。

表2 解耦算法的结果对比

Ⅱ类误差方面，LS 算法的最大Ⅱ类误差为2.655%，耦合误差较大。BPNN 算法的最大Ⅱ类误差为0.33%，ELM 算法的最大Ⅱ类误差为0.17%，与线性解耦算法相比，基于机器学习的非线性解耦算法能够有效降低六维力传感器的耦合干扰。IFWAELM 算法的最大Ⅱ类误差为0.13%，与ELM 算法相比，IFWA-ELM 算法在控制Ⅱ类误差方面有一定的提高，特别是在Mx、My、Mz方向上，Ⅱ类误差被控制在0.05%以内，耦合干扰得到了良好的控制。

根据解耦实验的结果，绘制箱形图，箱形图是一种通过5 个数字来描述数据分布的标准方法。如图8所示，6 个箱形图显示了传感器使用不同解耦算法后各方向的误差，箱形图的横线表示误差分布的最小、25%、50%、75%和最大分位数。“×”代表误差的平均值，“°”代表误差的离群值。使用IFWA-ELM算法解耦后，6 个方向的误差平均值和中值控制在0.1%以内，同时IFWA-ELM 解耦算法的误差数据更加集中。因此，本文提出的IFWA-ELM 算法的解耦性能优于LS、BPNN 和ELM，能够有效提高六维力传感器的测量精度。

图8 不同解耦算法的解耦误差箱形图

4 结论

本文提出了一种改进烟花算法优化极限学习机的解耦算法，利用改进烟花算法对极限学习机的初始权值和阈值进行优化。本文以应用于4 500 m 深海机械臂的六维力传感器为研究对象，进行标定实验。在标定数据的基础上，采用LS、BPNN、ELM 和IFWA-ELM 进行解耦实验。对比LS 和BPNN，IFWA-ELM 算法能够有效提高解耦精度，解耦后Ⅰ类误差控制在0.27%以内，Ⅱ类误差控制在0.13%以内。对比ELM 算法，IFWA-ELM 算法能够以更少的隐含层神经元获得更高解耦精度，且不易陷入局部最优解，具有更好的稳定性。实验结果表明:IFWA-ELM 解耦算法能够有效降低六维力传感器的Ⅰ类、Ⅱ类误差，提高测量精度。