思政元素融入大学数学课程的思考与实践——以微积分学课程为例

李静澎 张柳霞

2016 年12 月，习近平总书记在全国高校思想政治工作会议上强调，高校思想政治工作关系高校培养什么样的人、如何培养人以及为谁培养人这个根本问题。要坚持把立德树人作为中心环节，把思想政治工作贯穿到教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面。[1]育德与育才的辩证统一是在学校教育中难以回避的问题，是每位教师在教学过程中持续思考并不断实践的内容。课堂教学作为主渠道，应与思想政治理论课同向同行，形成协同效应。挖掘每门课程中所蕴含的思政元素，对于落实立德树人根本任务、实现价值引领具有积极意义。[2]

一、大学数学课程特点及融入思政元素的必要性

作为基础学科的基础，数学贯穿于人们的学习、劳动与生活，也为所有学科的发展提供力量，引领世界的改变。大学数学课程是高校开设的公共基础课程，也是很多专业的专业基础课程，其重要性不言而喻。大学数学课程的下述特点，决定其可以且应当成为思想政治教育的重要载体，承担起价值塑造、知识传授、能力培养的任务。

（一）课程开始时间早，持续时间长

由于课程的基础性，数学课程往往作为新生课程，在入学之初就进入学生视野，学习时间短则一学期，长则要延续到大学三年级（多为理工科学生）。课程的基础性和持续性既与数学课程本身的递进性特点有关，例如概率论知识的学习需要一定的微积分学基础；又与专业课程的需求结构有关，例如经济管理专业的学生学习经济学需要一定的微积分知识储备。数学课程的开始时间和持续性，使得借助其开展思政教育具备优势。大学阶段是学生人生观、世界观和价值观形成的关键阶段，新生进入大学学习，面临着转变身份、适应新环境的挑战，而他们的思维与人格品质等仍然不够成熟，面对外部环境的变化和复杂性，容易迷失或者迷茫。在学生学习数学课程的过程中，恰当地融入发挥价值引领作用的思政元素，将有益于学生在大学环境中逐步适应、调整状态、把握节奏并获得成长。

（二）专业支撑性强，应用性广泛

从专业知识储备的角度看，数学课程的理论、思路和方法是后续很多专业课程的知识基础和重要工具，数学学科本身蕴含的理性、逻辑、严谨、思辨的特质和结构化、步骤化的解决问题方式，也有益于学生素养和能力的提升。从应用范畴的角度看，社会经济、科学研究的方方面面都离不开数学知识。引入思政元素后的数学课程，可突出数学与科研前沿、社会经济生活、各行业专业领域的相关性，既能增进学生对专业的把握，又可增强对数学学科的认识。

（三）高度的抽象性，逻辑的严密性

抽象与严谨是数学学科的显著特点，大学数学课程则体现出更高程度的抽象性与逻辑的严密性，高度概括且严谨的数学语言、巧妙的证明思路、严格的推理在课程中一一展现，对学生抽象能力、逻辑思维能力的训练贯穿于课程的全过程。此时如果能把价值观、辩证思维、数学史等思政元素有机融入教学，既可增强数学知识的趣味性，有效调动学生学习数学的积极性，又可“如盐入水”般自然地实现知识传授、能力培养和价值引导。

（四）丰富的文化内涵

数学文化是指数学的思想、精神、方法、观点、语言，还包含数学史、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系等。[3]大学数学课程中蕴含着丰富的文化内涵，其文化教育价值为培养学生的科学精神、人文精神和数学素养奠定了基础。[2]大学生大多数经历了长达12 年的基础数学教育，难免在应试的压力下忽视数学的文化属性，进入大学阶段后，教师可突破学生长期以来将数学视为“解题训练”的惯性思维，将数学的文化属性在课堂上展示出来，这既能更好地激发学生学习数学课程的兴趣和动力，又能引导学生领略丰富的文化内涵，体现数学的人文教育价值。

二、思政元素与大学数学课程的结合点

每个学科专业的课程都蕴含着思政元素和育人资源，要在确保专业课程知识体系科学性和逻辑关系严密性的基础上，在遵循思政工作规律、教育教学规律、学生成长规律的前提下，把课程中蕴含着的思政元素挖掘出来并融进课程教学。[4]下文以大学数学课程开设内容中最为普遍的微积分学为例，阐述在大学数学课程中如何挖掘出思政元素并将之融入课程教学。

（一）哲学思维的植入

数学与哲学的关系密不可分。数学本身即是哲学思考产生的一个重要来源，为哲学的生存与发展提供了丰富的实践环境。[5]数学与哲学都来源于实践并作用于客观世界，二者相互影响、相互促进。数学的发展深刻诠释了“从生动的直观到抽象的思维，并从抽象的思维到实践”的过程，与辩证唯物主义认识论的“认识从实践中产生”“认识的真理性只有在实践中得到检验”等观点一致。

许多基本数学概念和方法都蕴含着丰富的哲学思想，伴随着课堂教学即可自然巧妙地植入哲学思维。例如微积分学中的极限知识点，描述极限定义的时候，需要从感性的认识、具体例子的推演、数学分析的语言、几何形态的描述等几个方面去反复释义，让学生对不断逼近、有限的变化、无限的变化进行深入的思考，逐步加深对于极限定义的理解。教学过程本身蕴含着有限与无限的对立统一、量变到质变的辩证规律等深刻的哲学思想。课程讲授全过程中既有极限定义的逐步深入讲解，亦可有效传递哲学思想，可于无形中进一步加深学生对辩证规律的认识和理解。通过引导学生总结归纳，更有利于提高学生的辩证思维能力，树立且形成辩证唯物主义的世界观与方法论。

（二）数学文化的融入

学生对数学知识的理解应该不仅仅包含学习数学知识的经验，而是应该建立在他个人具有的全部经验基础上。数学知识经历和其他各种经验经过整合并有机地联系在一起，形成他自己个性化的知识。在数学学习中，学生获得的不仅仅是显性的知识，如数学符号和法则，还包括隐性的精神、思想、方法和价值观念，后者服务于人的个性的不断成长。[6]学习数学的过程，可以成为接收数学所蕴含的丰富文化内涵的过程，其主要有以下途径。

1.数学史的嵌入

在课程讲授中适时嵌入数学史的知识，既可以让学生更好地理解数学的概念和方法，又可以在追溯数学工作者研究数学的历史过程中所处的背景、对人类社会的影响等时，将新知识的学习放在历史背景中展开，增加学生学习数学知识的兴趣，并引发其对相关历史背景的思考，达到滋养其人文素养的目的。

例如，在讲授导数概念的时候，往往以牛顿和莱布尼兹发现导数的过程为例，体现“数学来源于生活”“数学与实践之间的密切联系”。与此同时，教师可进一步介绍微积分发明权之争，指出牛顿的拥护者否认牛顿与莱布尼兹对微积分发明的独立贡献，坚持认为是莱布尼兹剽窃了牛顿的研究成果，对牛顿的盲目崇拜、对英国数学在国际上地位的盲目自信，导致了英国数学故步自封。[7]这在引起学生对导数概念兴趣的同时，也引发其对这一段历史中所折射出来的盲目又狭隘的民族主义所带来的负面影响的思考。

2.数学美的展现

数学类课程中充满着美的要素，概念之严谨、公式之简洁、定理之深刻、图形之匀称、理论之和谐、应用之广泛，充分展示着数学之美。[8]不论是心形线、星形线、螺旋线、马鞍面等数学图像所体现出来的直观上的美感，还是莫比乌斯带、斐波那契数列、黄金分割比等具有完美特征让人忍不住发出惊叹的数学现象，抑或是简洁的公式、严谨的定理，都在阐述着数学中的美感。教师可结合所授内容，将与数学之美有关的案例向学生展示，这既可以激发学生的兴趣，又可以使学生体会到数学之美的含义，从而提升审美能力，实现感性与理性兼具的审美感受。

例如，在讲授极限定义的时候，从描述性的定义到用魏尔斯特拉斯的定义，学生可以从中感受到数学的简洁之美；在讲授微分中值定理的时候，从罗尔定理、拉格朗日中值定理到柯西中值定理，教师可以分析三个定理之间包含与推广的关系，向学生展示数学定理之间的和谐之美；而多元函数微积分学部分，则可以通过引入空间图形的实例，例如广州塔“小蛮腰”（单叶双曲面）、广东星海音乐厅的屋顶（抛物双曲面），让学生直观感受数学图形的美感及其在社会生活中的广泛应用。

（三）对专业知识、生活实践的支撑

专业领域的知识、专业的应用前景等无疑是在校学生最为关注的问题，经过大学阶段的学习，学生终将迈入社会，将所学的专业知识应用于工作和生活的实践中。长期以来，受到应试思维的影响，很多学生对数学学科的认识停留在其“工具性”上，枯燥乏味的“刷题”模式让学生对数学的学习失去了兴趣，因而进入大学后很多学生对数学课程学习的必要性抱有怀疑态度，认为只要专业课程过关，数学课程无足轻重。另有一种看法是，摆脱高考即是摆脱了数学，数学只是高度抽象的数字游戏，与日常生活并无关系。而实际上，数学尤其是大学阶段的数学课程，对学生专业课程的学习以及进一步深造的支撑作用是不容忽视的。因此，教师需要在教学过程中将如下观念传递给学生：一是纠正学生对数学课程的态度，帮助他们正确理解所开设课程对专业课程的支撑作用；二是开阔学生对数学应用范围的思路，将实际应用问题转化为数学模型问题，改变学生对数学学科的认知；三是充分调动学生的积极性，引导学生参与到思考的过程中来，挖掘并归纳其中的数学思维模式，认识到知识的应用也许会有局限，但数学思想、数学方法的应用则广阔且深远。

数学课程中很多知识点与专业领域相关，二者的有机融合可以在课堂中以引例、数学模型、案例分析等方式得以呈现。例如，经济学中均衡价格、边际成本、边际利润、需求价格弹性等概念都和函数及其导数有关；社会经济问题中的评价模型需要基于指标体系、采用一定的赋权方法才能得以应用；定性数据的分析离不开对均值和方差的理解，而定性描述向定量数据的转化无疑需要数学概念和方法的帮助。解读生活中的现象与问题同样离不开数学，例如与人们生活密切相关的房价拐点、疫情时代新闻媒体上频频出现的疫情拐点，都应该建立在对“拐点”这一概念的正确解读和认知上，才能突破认知的盲区，避免错误理解。

（四）价值观的塑造

大学阶段是塑造学生世界观、人生观、价值观的重要阶段。在当今社会复杂深刻的国际形势、多元文化思潮冲击的背景下，大学生接收信息的渠道广且速度快，十分有必要在课堂教学的过程中，将爱国、敬业、诚信、友善等社会主义核心价值观融入其中，让学生接受正确的思想引领。教师可将有益于学生价值观塑造的思政元素融入课程教学，具体可有以下方面。

1.提升学生的民族自豪感、爱国情怀与文化自信

中国古代数学的辉煌成就、古典文学中蕴含的数学思想、当代中国科技取得的巨大成就中数学的强有力支撑，这些案例可以在教学中恰当融入，提升学生的民族自豪感和责任感，激发爱国情怀，增强文化自信。

例如，讲授极限概念的时候可以将刘徽的割圆术以及祖冲之在此基础上计算圆周率的故事作为引例，指出这一成就比法国数学家韦达的成果早一千多年；讲述定积分的时候，引入祖暅利用刘徽的“牟合方盖”理论去计算体积，并提出了著名的祖暅定理——“缘幂势既同，则积不容异”，比意大利数学家卡瓦列里提出的卡瓦列里原理早一千年；中国高铁的快速发展被国人引以为傲，高铁的平稳运行离不开“曲率”的概念，此外在航空航天、信息技术、材料科学等领域，都离不开数学的贡献；而李白著名的诗句“孤帆远影碧空尽，唯见长江天际流”，则可以引导学生感受古代文学与极限思想的完美结合。

2.引导学生建立理性、客观与诚信的态度

严密的逻辑性是数学的特点，数学课程的学习对于引导学生理性思考、在纷繁杂乱的信息面前保持客观具有积极的作用。如果能再结合生活实际进一步引发学生的思考，对于塑造其科学诚信的价值观会更为有益。

例如，微积分中第二个重要极限与连续复利模型密切相关，教师可以先讲解知识点，再指出当前消费贷、校园贷陷阱频发的社会现象和具体案例，引导学生利用复利模型去分析其背后高利率与高风险的隐患，引导学生树立正确的消费观，避免高息贷款的陷阱。讲授极限计算著名方法——洛必达法则的时候，则可以适时引入洛必达法则发明背后的故事，向学生介绍洛必达法则实际上是约翰·伯努利发现的，但最终却被命名为洛必达法则的缘由，由此引导学生关注学术诚信问题。

3.激励学生勇于创新、敢于面对挫折、不懈求真的精神

数学知识中蕴含着很多做人的道理，只需在课堂教学的过程中稍做提示，或者鼓励学生归纳总结，引导学生讨论分享，即可达到育人的目的。借助数学概念，可引导学生端正态度，勇于挑战，敢于面对挫折。例如讲到极值的概念，可以提到极值如同人生起落，要正确看待人生的每个阶段，遇到挫折时不要悲观绝望，取得成绩时不要骄傲自满，无论低谷还是顶峰，都是新起点。而新思路新方法的提出，即可凸显创新精神的重要性，例如引入定积分概念时，通过分割（化整为小）、近似（以直代曲）、求和（化小为整）、取极限（精确化），可以引导学生用所学知识解决新问题，鼓励创新意识。数学计算追求严谨，必须考虑全面，否则将“失之毫厘，谬以千里”，以此鼓励学生不懈求真。

三、微积分学课程教学中融入思政元素的实践与反馈

（一）以极限定义为例的课程思政实践

一般而言，微积分学课程于大学一年级开设，主要涵盖极限、导数与微分、不定积分与定积分、多元函数微积分学等内容。其中极限的定义是连续、导数、定积分等知识的基础，在整个微积分的学习中具有贯穿全局的重要作用。于学生而言，极限是大学生学习数学的第一个新知识点，一般在开课的第1—2 周开始讲授，与新生适应大学生活的节奏同步，同时又因其高度的抽象性而成为学生学习微积分学课程所面临的第一个挑战。在极限部分的课程讲授中，恰当融入思政元素，开展课程思政的教学实践，将传授知识、价值塑造、能力提升融合在一起，可以使学生在理解概念的同时，进一步强化对学科的认识，助力其价值观的塑造。这既具有恰当的契机，又具有现实的可操作性，并可进一步检验课程思政实践的效果。

2022—2023 学年秋季学期，笔者讲授三个专业、两门涉及微积分学教材的数学课程，分别是人力资源管理专业本科、会计学专业本科的《经济数学——微积分》以及数字媒体技术专业的《高等数学Ⅰ》。在极限定义部分的讲授中，课程思政主要从以下四个方面切入。

1.极限定义的引入

以刘徽的割圆术作为案例引入极限概念，提升学生的民族自豪感和爱国情怀。

案例具体如下：刘徽是魏晋时期伟大的数学家，中国古代数学理论的奠基人之一，公元263 年写了著名的《九章算术注》。在该书中刘徽创立了“割圆术”这一新的数学方法：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这一方法其实就是极限思想的体现。进一步提及中国古代数学家在圆周率计算方面的成就：到了南北朝时期，祖冲之在刘徽研究的基础上继续努力，使圆周率精确到了小数点以后的第七位；在西方，这个成绩是由法国数学家韦达于1593 年取得的,比祖冲之晚了一千一百多年。

通过刘徽割圆术的展示，引导学生建立对极限思想的直观感受，同时介绍了中国古代数学的辉煌成就，以此引发学生的民族自豪感，进一步激发学生的爱国热情，激励学生学以致用，为中华民族的复兴而努力奋斗。

2.极限定义的描述

通过极限定义的描述性分析，揭示有限与无限、量变到质变的思想，引导学生加强对辩证唯物主义世界观和方法论的认识，提升学生的思维能力。

数列部分是学生在高中阶段学习过的内容，课程讲授中以具体数列作为切入点，例如数列，通过n＞10，n＞100，n＞1000 等情况，解释un与1 的接近程度，以此来逐步归纳出数列极限的直观描述，使学生对数列极限产生具象的体会，建立由具体到抽象的数学思维模式，同时感受有限与无限的对立统一、量变到质变的辩证规律，体会数学中蕴含的哲学思维。进一步，在讲授ε的任意性和暂时固定性时，让学生体会到事物的两面性，建立多维度看待问题的思维方式。

实际上，微积分学中，整个极限部分的内容都充分体现了辩证唯物主义的哲学思想，包括极限定义之后涉及的无穷小与无穷大、函数连续等内容。学生通过反复学习、思考并且应用极限思想，对其哲学思维品质的提升无疑是有益的。

3.极限定义的提出

数列极限的“ε-N”、函数极限的“ε-X”“ε-δ”等定义的描述与对比，展露出抽象、严谨兼具的数学特性，呈现了数学学科的简洁之美。

极限的定义可以使学生感受到微积分学高度抽象和逻辑严密的特质，但部分学生表示这部分内容难以理解。此处教师可以多次重复、反复“渗透”，以对比及类比的方式逐步加强学生对这一定义的理解，同时要强调这一定义所呈现出的数学之美：简洁之美、严谨之美，让学生体验数学学科的魅力。

4.极限定义的理解

利用古诗词中蕴含的极限思想，加强学生对极限思想的理解，并体会到数学之美。唐朝诗人李白的名篇《黄鹤楼送孟浩然之广陵》中有一句“孤帆远影碧空净”，正是极限思想的体现，如果把帆影的长度看作一个函数，这句诗描述的正是函数极限为0 的情况。这个案例巧妙地将古代诗词与数学知识结合起来，既有助于学生更好地理解函数极限，又增加了数学的文化属性，让学生体验到数学之美。同时，这句诗词反映出的内容恰是“无穷小”，可作为后续课程的一个铺垫，体现出课程思政的延续性。

上述四个方面，除“割圆术”部分需要通过课件具体展示，占据一定时长外，其余内容均只需在授课过程中“点到即止”，既不会由于占用过多学时而影响教学进度，又可落实思政教育目标。

（二）思政元素融入大学数学课程实践的反馈

思政元素在课程中的融入，既要尊重学科的特征，又要符合学生的特点，尊重学生的需求。在教学实践过程中，为更好地把握学生对于学科和课程的认识，检验课程思政的实践效果，了解学生对课程学习的需求和期望，笔者在经过一段时间的课程思政教学实践之后，采用调查问卷的形式，对所授班级学生展开了调研。

调研的基本情况为：在讲授完“数列极限、函数极限定义”之后，讲授“无穷小量与无穷大量”之前，在课堂教学开始前完成问卷发放。利用“问卷星”软件在学生微信群中发放问卷，学生人数共计120人，最终回收问卷112 份。

调研主要围绕两部分内容展开：第一部分是学生对极限部分涉及的课程思政相关内容的反馈，包括对“刘徽割圆术”案例的反馈和学生对极限概念所蕴含的哲学思想、体现的学科特点的感受；第二部分是学生对数学学科的认识，包括数学学科的特征、数学与生活、专业的关系等。此外，为了更好地开展教学工作，围绕学生对课程学习是否有信心、既往数学学习中有何经验、目前学习中存在的困难发布了相关问题，其中经验和困难部分主要用于教师教学过程的参考，其内容本文不再赘述。

1.对“刘徽割圆术”案例的反馈

表1 呈现了学生对“刘徽割圆术”案例的部分反馈，可以看出这一案例对学生的触动比较大：一方面通过割圆术的展示和描述，学生对极限思想有所理解；另一方面，古代数学的辉煌成就激发了学生的民族自豪感，增强了文化自信，也触动了学生的爱国热情。

表1 部分学生对“刘徽割圆术”案例的反馈

2. 对极限概念所蕴含的哲学思想、体现的学科特点的感受

极限概念是微积分的基础，其中蕴含着丰富的哲学思想，充分体现了数学学科的特点。 笔者在问卷中提出“通过极限定义的学习，你认为从中体会到了以下哪些方面”的问题，并给予选项，表2 列举了学生对所给选项的感受情况。 数据反映出通过极限概念的讲授和分析，确实可以促进学生对哲学思想的挖掘和体会，强化学科特点的显现，这对于提升学生思维品质不无裨益。

表2 学生对极限定义的理解和认识

3. 学生对数学学科特点的认知

表3 体现了学生对数学学科特点的认知。 从表中可见，学生对于数学的严谨性、抽象性、简洁性、蕴含哲学思想、蕴含美感的认可程度普遍较高，经过多年数学课程的学习，学生对数学学科特征的认识比较清晰，个别特征上的感受略有不同。

图1 将持有“认同”和“非常认同”观点的数据进行汇总， 观察学生对数学学科特点的认可程度。可以直观地看到，认可程度最高的是严谨性，认可程度相对较低的是简洁有力和数学美。 可见有必要在教学过程中进一步通过实例融入数学之美，呈现数学的广泛应用性，以促进学生对数学学科认识的多元化。

图1 学科特点认知数据比较

4. 学生对数学学科与生活、专业关系的态度

表4 显示了学生对数学学科与生活、专业关系的态度。 与学科特点调研中大多数学生表示认同或非常认同的统计结果不同，在数学与生活、专业、工作等方面关系的态度上， 有相当数量的学生持 “一般”态度。 这一结果反映出学生对数学课程的实用性认可度不高，也与学生群体中“数学无用论”的看法存在一定程度的吻合， 这必然导致学生学习动力和兴趣的不足。 该结果提示，教师需要在课堂中注重传递数学对各学科的支撑及对个体未来生活和职业生涯发展的积极支持作用， 从学习动机角度去提高学生的学习意愿。

表4 学生对数学学科与生活、专业关系的态度

5. 学生学习数学课程的信心程度

图2 体现了学生对数学课程学习的信心状态。整体来看，大部分同学对课程的学习有一定程度的信心， 非常缺乏信心和缺乏信心的学生占比总计为15.17%。 这提示教师要注重引导，鼓励学生更多参与课堂，课后加大对部分学生的指导，以增强学生对课程学习的信心。

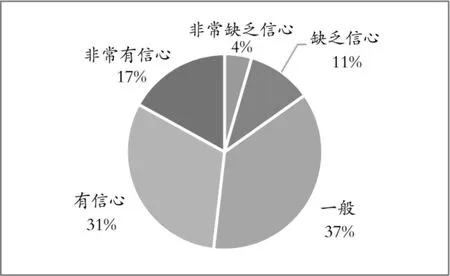
图2 学生学习数学课程的信心程度

上述调研数据体现出，通过将思政元素融入极限定义的教学中，可以较为恰当地处理知识、能力、情感态度和价值观三者之间的关系，证实了微积分学课程思政的可行性与有效性。 调研数据也反映出学生对数学学科的认识和学习的信心，对于指导教学实践具有参考价值。

综上所述， 课程思政是落实立德树人要求、实现“三全育人”的需要，也是学生德智体美劳全面发展的需要。 本文在理论分析与具体课程实践的基础上，以调研数据验证了课程思政实践的效果，从而得到以下启示：作为大学教师，在教学实践中，要持续深入挖掘思政元素，寻求思政元素与课程教学内容的有机结合，不断提升教学水平，落实立德树人根本任务。