降低永磁同步电机滞环控制电流波动的方法研究
2024-01-26唐敬亮关玲玲李文耕
唐敬亮,关玲玲,张 程,李文耕
(1.兰州飞行控制有限责任公司 西安研发中心,西安 710100; 2.兰州飞行控制有限责任公司 九分厂,兰州 730070)
0 引 言
永磁同步电机(以下简称PMSM)是电机伺服控制领域的研究热点,速度-电流双PI控制可以确保最终的速度和dq轴电流都处于无差跟踪状态(阶跃速度给定),并具有良好的稳态性能[1],因此在PMSM中得到了广泛的应用。然而,级联速度-电流双PI的控制结构降低了系统的动态性能,其稳定性应精心设计。有一些学者也使用了滑模控制和模型预测控制等方法来提高矢量控制[2-3]的动态性能,但这些方案复杂程度更高。
作为一种简单的电流回路控制器,滞环电流控制(以下简称HCC),由于其结构简单,动态响应性能好,对系统参数变化不敏感,软件和硬件实现简单,无条件稳定,已广泛应用于各种电机的矢量控制和并网逆变器[4-19]。然而,对于PMSM,电机电感小易造成HCC波动显著。
当采用固定环宽HCC,通过在α,β轴上设置两级滞环可以限制HCC的电流波动,并采用0矢量降低稳态电流波动[15]。在此基础上,分别在α轴和β轴上设置了4级和3级回滞比较器,进一步优化了系统性能[12]。这种方法是通过模拟电路来实现的。PMSM的磁场定向控制(FOC)通常通过数字控制系统进行,其采样频率不能过高,电流的滤波器和程序的执行会带来延迟,若逆变器不能及时动作输出电压,那么电流的波动就会变大。
变环宽的方法主要是通过数字电路实现,其更适用于PMSM控制领域。采用一种简单的方法计算环宽,减小了逆变器[4]开关频率的波动。回滞宽度是在线计算[8,16-17]。时钟信号和PWM载波用于辅助回滞过程,以完成对逆变器开关的控制[10]。与七段SVPWM类似,可以输出逆变器开关模式,实现PI控制的稳态性能和回滞的速度[8,10,16-17]。然而,这些特性将需要一些额外的硬件电路[10]。在文献[4,8,16,17]中,高采样频率(高于10倍开关频率)被应用以及时减少逆变器的电流波动。因此,逆变器开关频率较低,电流谐波较大。
当数字电路实现HCC时,电流波动很大的原因是在整个PWM周期内实际上只使用了一个空间电压矢量,控制周期不能太短,导致电流剧烈变化。特别对于PMSM(由于绕组的电感较小),这种情况被放大了。为此,考虑采用PWM时,在一个控制周期将有多个电压矢量来减少电流波动。
数字系统的采样周期性会导致执行延迟。为了进一步减少电流的波动,应注意尽可能补偿这个节拍延迟。
一种想法是间接补偿。增加一个电压补偿项,以减少延迟对稳态性能[24]的影响,观察器用于补偿延迟[25-26]。然而,这些方法需要精确的运动参数,实现起来比较复杂。另一种方法是直接补偿。传统的直接补偿策略是基于数学模型来预测下一拍的轨迹[20],但它对系统参数的变化更为敏感,预测需要较长时间。文献[21-22]中利用空间电压矢量在短时间内产生近似恒定的效应,不需要系统参数,减少了预测时间,预测精度得到了提高,但它不适用于电压矢量合成的方法。
文献[23]利用了PWM的特性,在一个PWM循环中,合成的电压矢量波也是中心对称的,将预测时间减少到半拍,并且不需要系统参数。当系统稳定时,每个拍的给定电压近似等于反电动势,因此该方法对测量噪声非常敏感,且半拍的预测时间是固定的,不能改变。
针对HCC控制PMSM电流波动大的问题,本文提出了一种基于PWM矢量计算输出的方法来解决传统HCC中电流波动较大的问题。放弃根据开关表选择电压矢量输出的方法,采用计算输出电压。当实际电流超过滞环误差带时,根据回滞比较器的输出值,对d,q轴的输出施加适当的电压,使电流能够快速返回到误差带以内。当电流在误差带以内时,将使用PI的不连续积分来控制输出电压。PI的积分器将只在当前的变化超出预期的情况下起作用。PI控制器可以设置与比例系数一致的积分系数,所以积分器的值比传统的PI更快地收敛到稳态。此外,当前的变化满足预期时,PI控制器不进行积分,这缓解了PI控制的超调和振荡现象。最后,在稳状态下,电流总是在给定电流周围波动。
对于数字延时问题,在分析了三相电压的相互耦合关系后,利用PWM的对称性,在一个周期内进行三次采样,可以完成对系统执行延迟的补偿。
1 基于d,q轴PMSM HCC
为了简化分析,本文采用表贴式PMSM进行研究。
定子电压表达式:
(1)
式中:所有参数基于d,q坐标:id和iq是定子电流;ωe是角速;L和R是绕组的电感和电阻;Ψf是励磁磁链。
转矩表达式:
(2)
根据HCC,在d,q坐标系中设置一个误差方形区域,然后根据d轴和q轴的两个回滞比较器的输出,选择合适的电压矢量。电流将连续跟踪给定的电流矢量,方法结构如图1。
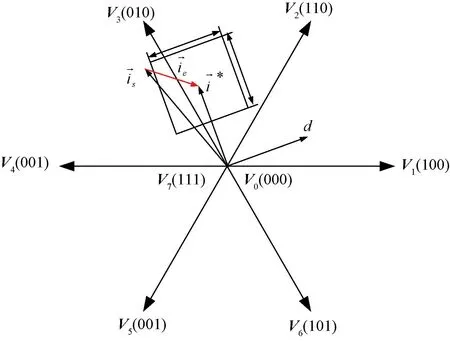
图1 基于d,q轴传统HCC调节方法
给定电流i*的方向与q轴对齐,参考FOC控制中isd=0。以给定电流顶端在d轴和q轴分别设定误差带,通常d轴和q轴误差带设定相同,如此便可看到图1所示方形误差区域。依据d轴和q轴的回滞误差,在8个空间矢量中选择最优的一个,计划将实际电流拉回或保持在方形误差区域内。如图1中,采样电流已超过d轴的左极限,根据式(1)所述,为了使电流返回到公差区域,所选的电压矢量必须有一个正的d轴分量(将d轴电流向右拉)。考虑到反电磁势会使q轴电流下降,这样,就可以根据可能超出公差范围的电流对开关表进行总结,并可以进行回滞控制,具体方法见文献[11]。
2 提出新方法
2.1 根据滞环选择输出电压
如基于d,q轴HCC所述,这种矢量选择策略可能导致电流在控制周期内波动太大。原因在于单个周期内空间电压矢量选择单一,并且PMSM绕组电感明显较小。因此,本文放弃了选择单一矢量的方法,采用了矢量合成。
根据回滞比较器的输出,直接得到d,q轴的输出电压。回滞比较器的输出值的计算方法如式(3)所示:
在式(3)中,带星*上标的参量为参考电流,输出为回滞比较值(0,1,或2)。实际输出d,q轴电压见式(4)。
(3)
(4)
Udb和Uqb是计算出的施加电压,以减少电流波动,它们的计算将在后面给出。当采用isd=0控制策略时,Risq和ωLisq都较小。所以当d轴电流超过公差范围时,一个小的Vd可以使其迅速返回到公差范围。±Udc/3作为输出电压是足够的。
对于q轴,反电动势对q轴有更大的影响,从而降低q轴电流。因此,当q轴电流较小时,其输出为2Udc/3 (SVPWM调制所能输出的最大电压幅值),从而使q轴电流快速跟踪参考值。
2.2 输出电压计算
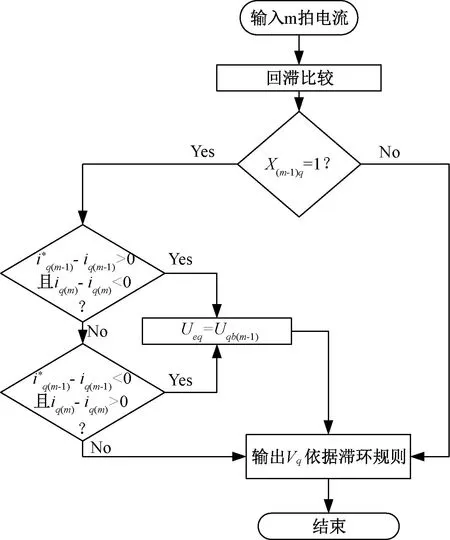
当实际电流进入误差范围时,为了减少电流的波动,希望实际电流能够连续地跟踪参考值,而不是像传统的HCC那样保持0向量,直到电流达到回滞范围。因此,当Xd和Xq为1时,输出电压Udb和Uqb由在线计算确定。从而使实际电流总是在给定的周围波动。
离散化式 (1)可得到以:
(5)
式中:Δid和Δiq是d,q轴电流在一拍中的变化量;ΔT是一拍的周期;m是拍数。
为了使得实际电流始终跟随给定值,当滞环输出为1时,Udb和Uqb由应满足:
(6)
式中:Ued和Ueq是d,q轴误差电压;K是比例系数;id(m)和iq(m)是id和iq给定第m拍的值。当实际电流在误差域以内时,式(6)减去式(5)可以得到式(7):
(7)
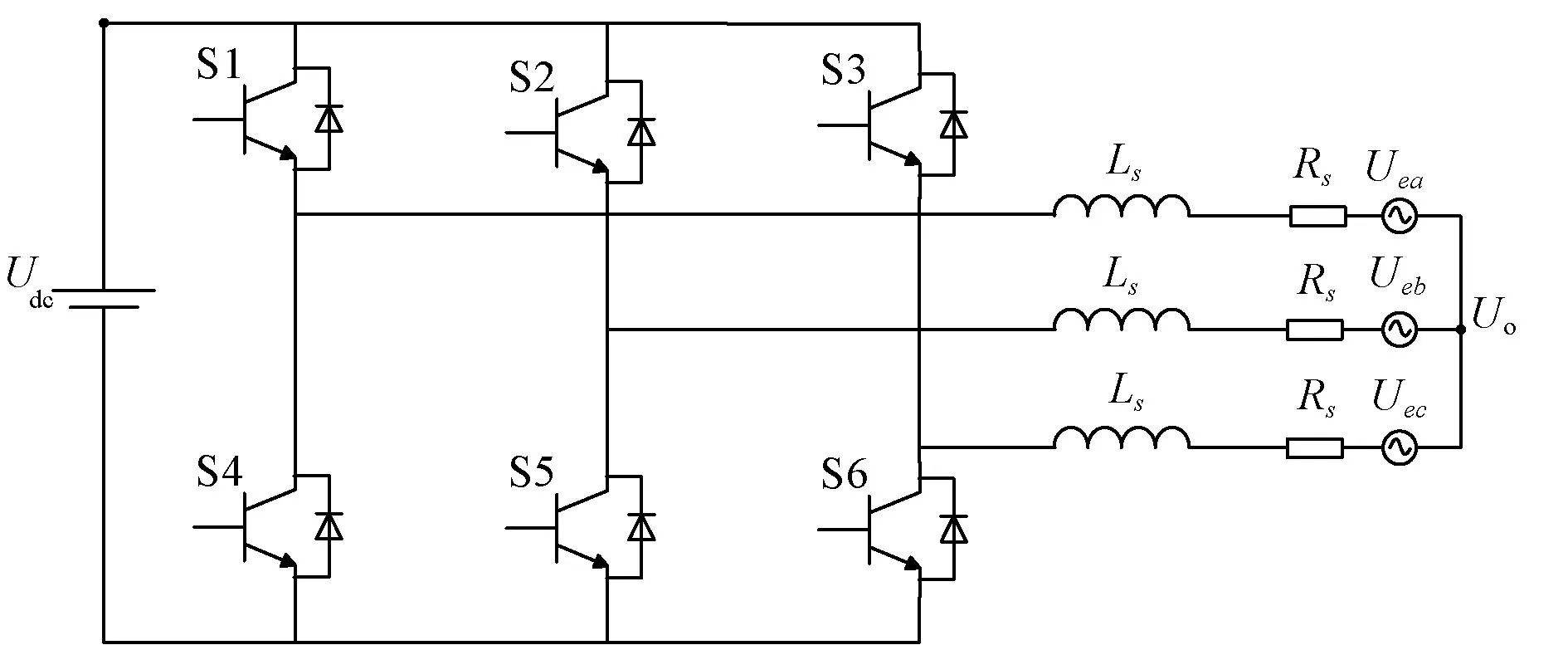
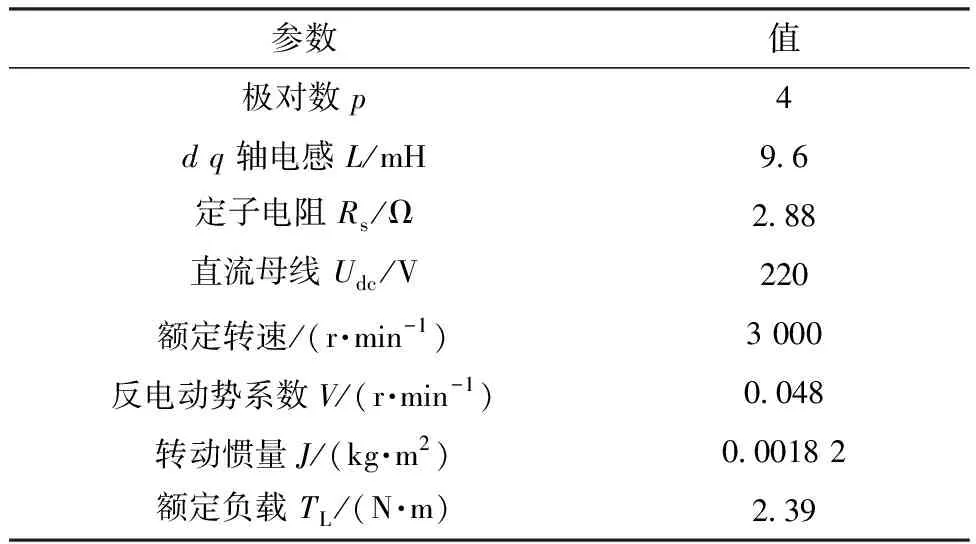
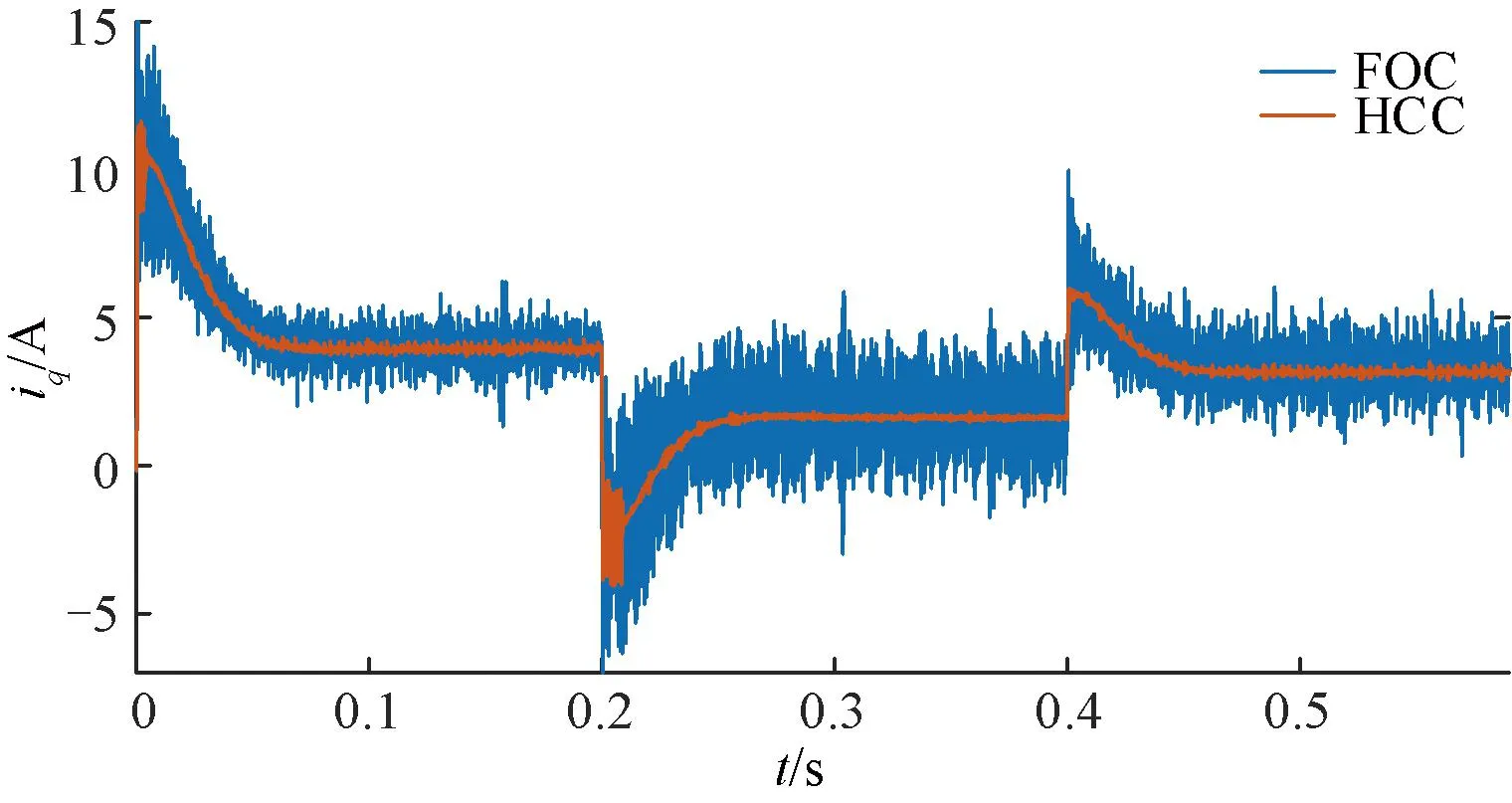
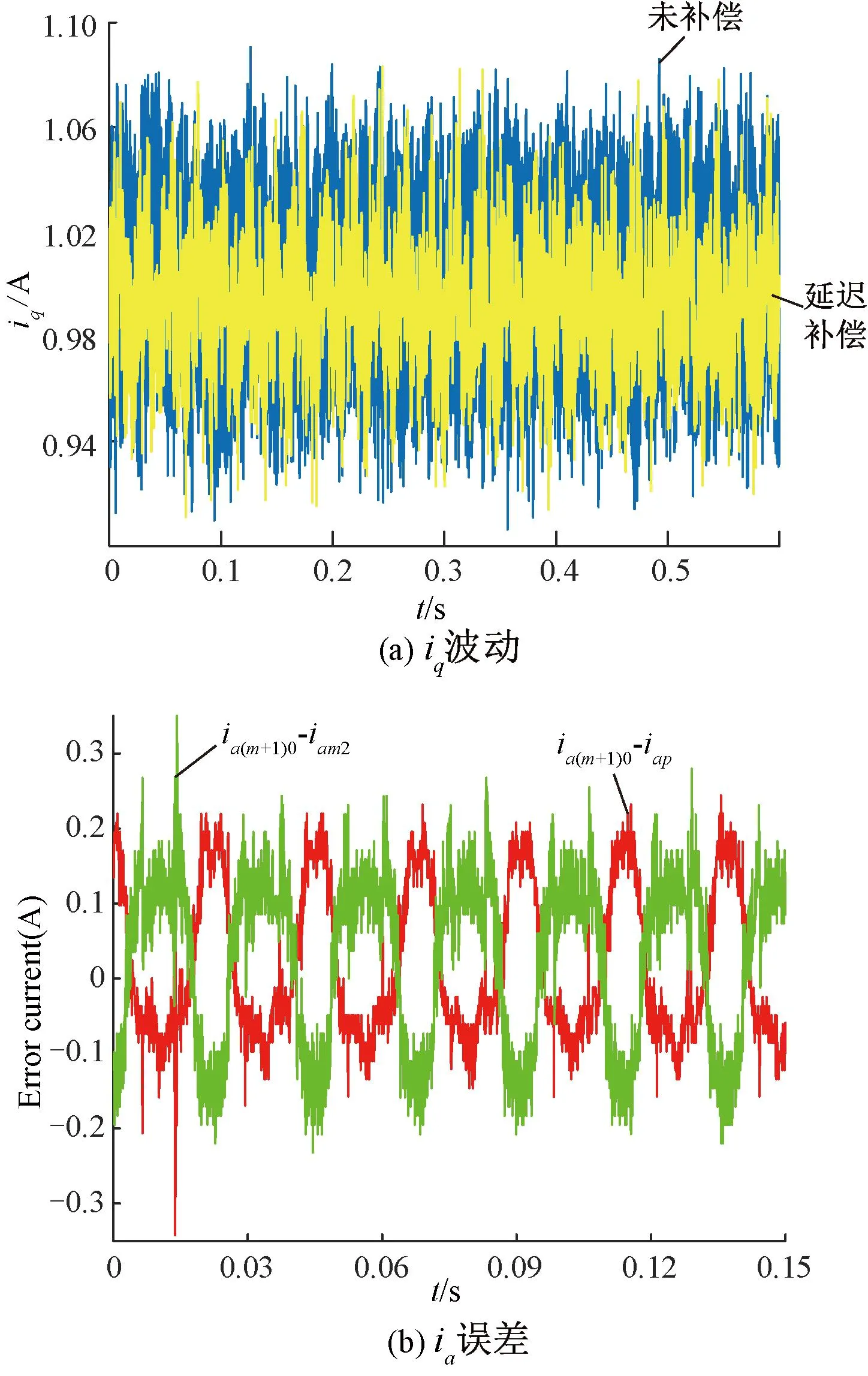
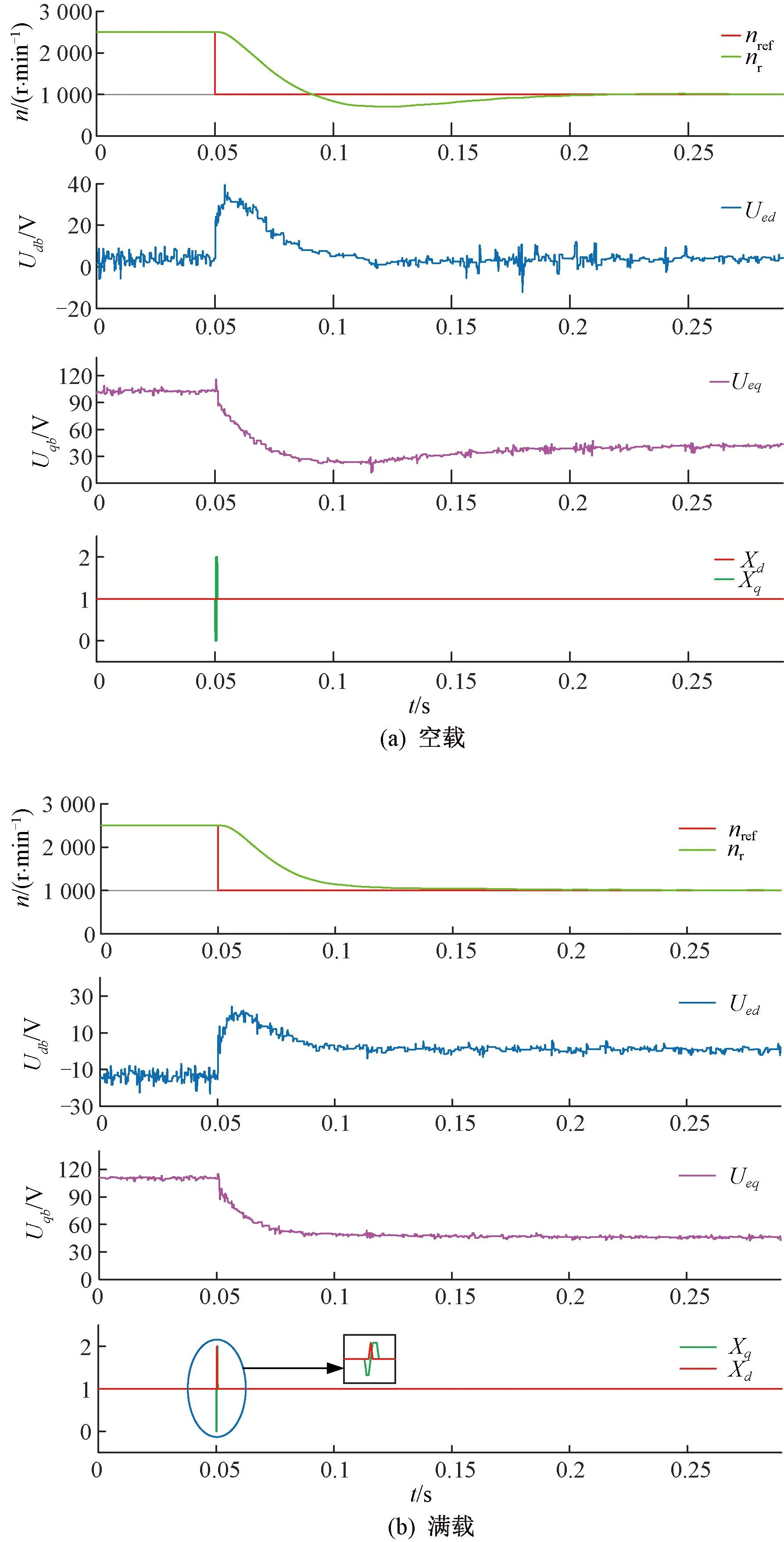
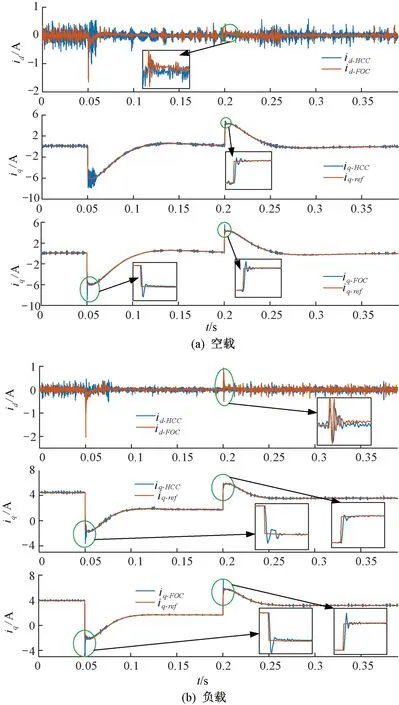
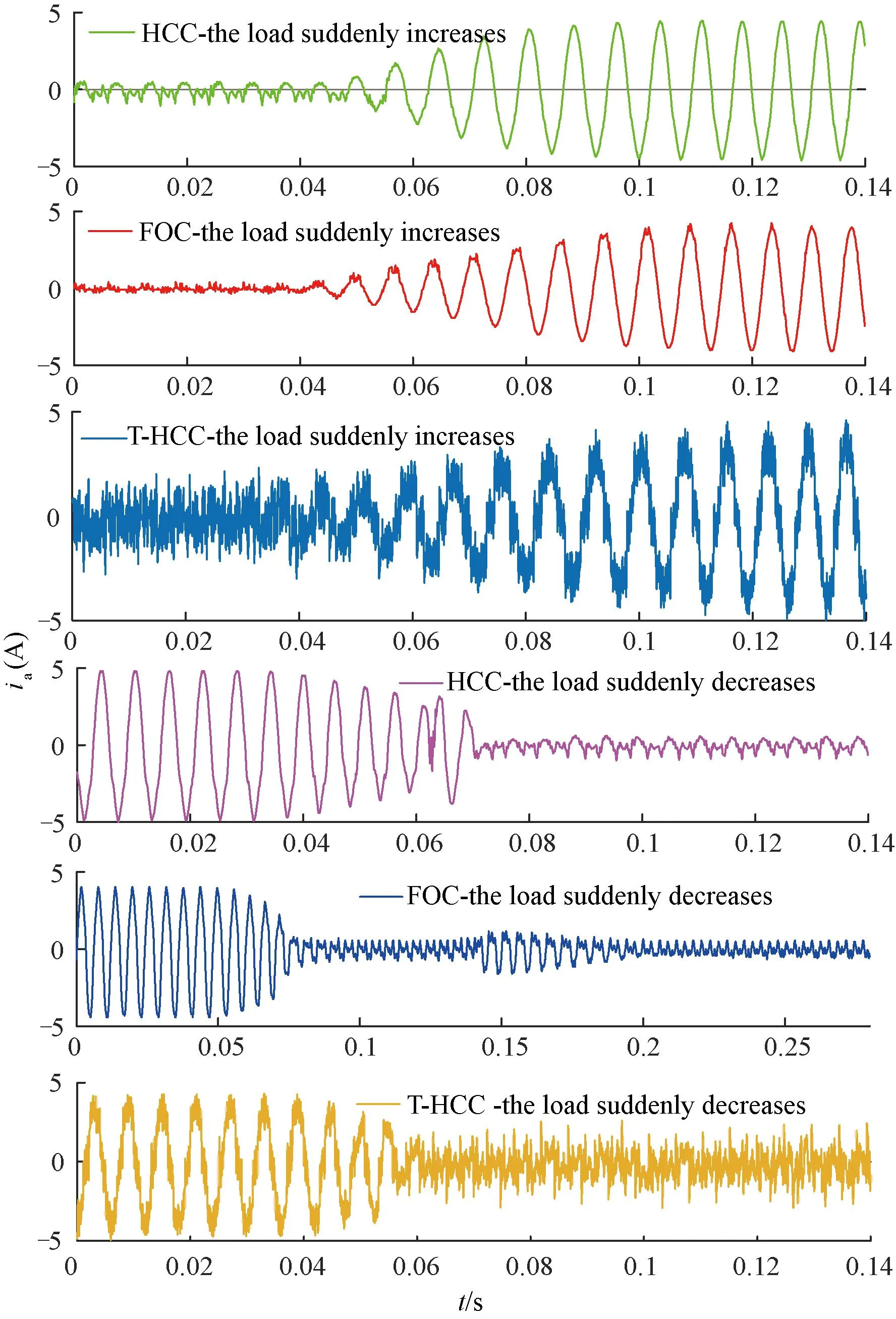
根据式(7),K应该取L/ΔT。此时,系统的响应速度是最快的。但是,K是根据式(7)直接计算的,在考虑到数字系统的单拍延迟后,系统的稳定性是一个值得注意的问题。HCC从本质上保证了系统的动态性能,K应该满足K q轴电流参考值是由速度环PI控制后获得的,它在稳态下也会波动,很难有效地跟踪其参考值,因此,修正式(6)为: (8) 式中:b是一个小电压常数,用以尽可能减小误差;sign定义如下: (9) 2.3Ued和Ueq估计 至此,依据式(6)就可得到Udb和Uqb,从而式(4)的输出明确。然而,基于式(6)的PMSM模型参数计算需要电机参数,这削弱了HCC对系统参数不敏感的优势。因此,本文又设计了一种基于双采样电流变化信息的不连续积分策略来进行估计Ued和Ueq,将估计值代替实际值输入(8)计算输出电压。 (10) 如果Δiq(m)<0,就会得到: (11) 从式(11)中可知,在Ueq和估计值中存在误差,接着需进行积分。更新Ueq估计,如下式: (12) 当Δiq(m)>0,Ueq和估计值的误差不能准确判断,所以积分器不工作。将式(12)代入式(8)并计算。b值不应太大,以免导致估计精度下降。考虑到设置b的主要目的是处理在稳态下由于转速的轻微变化而引起的电流变化,则b应该满足: b≈L·max(Δiref)/ΔT (13) 式中:max(Δiref)是稳态下参考电流的两拍之间的最大变化。由于速度波动范围也会随工作条件而略有变化,max(Δiref)只能估计,所以在(13)中使用“≈”。 只要回滞宽度不设置得太窄,在系统达到稳态时,回滞比较器的输出始终为1,电流波动仅取决于逆变器的开关频率和b值,与回滞宽度无关。 当回滞比较器的输出值为1时,Ued和Ueq二者的估计计算与传统的PI控制方法有一些相似之处。但该方法最显著的特点是积分的不连续。实际上,考虑到稳态后的电流误差几乎为零,由理想状态下的PI积分器得到的Ued和Ueq,与本文的估计计算结果相似。但很明显,本文中积分器的作用取决于前一个节拍的当前变化,这更为合理。与传统的PI的积分器相比,不连续积分只增加了一个判断条件。两者的软件复杂度大致相同。本文设计的不连续积分流程如图2所示。 图2 不连续积分流程图 从图2可以看出,本文提出的不连续积分需要m拍和m+1拍的当前信息,这两拍之间的电压输出值为Udb和Uqb,由m拍计算得到。由于DSP的EPWM输出有一个节拍延迟,如果执行延迟没有得到补偿,则需要一个更复杂的程序逻辑来消除该节拍延迟对积分器的影响,这会导致比例部分的输出不当,因此有必要补偿延迟,以保持一个简单的系统结构。为此,本文提出了一种新的延迟补偿策略,该策略对测量噪声具有鲁棒性,且不需要系统参数。 图3 三相两电平VSI结构 三相逆变器的结构如图3所示。Rs和Ls分别为相电阻和电感。Uea,Ueb和Uec分别为A、B、C相的反电动势,U0为中性点电压,有关系如下: (14) 式中:x={a、b、c}表示三相下标;Ux为线电压;ix为相电流。假设在一个节拍中Rsis和Uex保持不变,根据PWM的对称性,可以直接推导出下一个节拍开始时的相电流,如图4所示。 图4 电流预测时序图 三相逆变器的三角载波和三相占空比波形如图4所示。中间部分的三相方波为相电压波形,底部的蓝线是a相电流波形。根据伏特-秒等效原理,从Tm0到Tm1,有Ub=Uc=0,并且Ua=(ΔT1-ΔT0)/ΔT1。ΔT0是Ua=0持续时间,考虑到式14中的U0,则三相电压为: (15) 每相电流在ΔT1内的变化是可以获取的。可以得到各相电流的变化。在图4中,A相电流变化被给出如Δia1。从PWM的对称性可以看出,在三角形载波峰的右侧,可以找到时间Tm2,从Tm2到下一拍起始T(m+1)0,有ΔT1=ΔT2。在ΔT2期间,三相电压也满足式(15)。然后电流变化量Δia2=Δia1。这一结论适用于三相计算。 因此,下一个节拍开始时间的电流ix(m+1)0可以直接从电流ixm0,ixm1和ixm2(在Tm0,Tm1和Tm2时刻采样值)推导出来,如下所示: ix(m+1)0=ixm2+ixm1-ixm0 (16) 从以上分析中可以看出,为了实现无执行延迟的效果,需要合理安排当前循环的计算程序的执行时间。它必须在ΔT2内完成。在Tm2开始前,可以先完成速度环计算。 与文献[23]的预测方案相比,本文多进行了一次电流采样。然而,电流的预测是基于相-电压耦合关系,而不考虑由三相PWM合成的矢量,三次采样的时间更加灵活,合适的ΔT1和ΔT2可以在满足程序执行时间的要求下设定,从而避免测量噪声因Δia1小而影响较大,因此本文方法对采样误差更有鲁棒性。 下面将本文方法(以下简称HCC)与传统的PI双闭环方法(FOC)进行了比较,还给出了传统的HCC方法(以区别于本文提出的方法,以下称为T-HCC)。实验设备平台如图5所示。实验采用以DSP28335为控制芯片的控制器,开关频率设置为10 kHz。除延迟补偿的验证部分外,在其他实验中不使用延迟补偿,因此ixm2替代ix(m+1)0被直接用于计算。Tm2和T(m+1)0之间的间隔为1/3控制周期(33.33 μs)。为了公平起见,还对传统的对比速度-电流双PI的电流在Tm2进行采样,使延迟对两种方法影响相同。 图5 测试平台 实验中使用的电机数据见表1。电机是表贴转子。电机所承载的负载为线性负载。当转速为2 500 r/min时,额定扭矩为2.39 N·m。 表1电机参数数 在实验中,K=36,回滞宽度为ihd=ihq=1 A。该方案与传统PI的速度回路PI参数一致,分别为Kp=0.004,Ki=0.000 006;与传统PI方案的电流环路PI的两组参数进行比较:其中一组Kp=Ki=36(参照K值),另一组值根据文献[27]计算,为Kp=36,Ki=1.63。所有实验均采用isd=0方案。为更说明问题,T-HCC的控制频率为40 kHz,回滞宽度为ihd=ihq=0.2 A,其他参数与HCC一致。 传统的PI (FOC)电流回路参数均采用Kp=Ki=36,参考速度为2 500 r/min;在0.2 s时,速度命令为1 000 r/min,在0.4 s,上升到2 000 r/min,带载启动。两种方法的q轴电流波动如图6所示。此时,FOC(较高的参数)和HCC的动态响应一致,但电流波动比HCC大很多。 图6 q轴电流对比(FOC和HCC) 图7 延时补偿结果 图7(b)为预测值iap与ia(m+1)0之间的误差,以及iam2与ia(m+1)0之间的稳态误差。误差曲线周期性波动,iap和iam2之间的波动范围较小。 从图7可以看出,经过延迟补偿后仍会出现一定误差。这是由于参数如反电势,电机电感矩阵等,将随着转子的旋转而有一定改变,得到的结果是误差的正弦变化。ia(m+1)0与其预测值iap(m+1)的误差: ea=ia(m+1)0-iap(m+1) (17) 由于ea的频率与基频一致,即在两个控制周期内基本没有变化,因此,可以认为ea也包含在补偿中,如下所示。 i′ap(m)=iap(m)+ea(m-1) (18) 式中:iap(m)是A相在m拍起始电流值(依据式(16))。对于延时补偿用i′ap(m)替换iap(m)更为合适,但由于实验条件有限,随机测量误差(图7(b)中波形出现的差错)对计算产生负面影响,最终的实验结果没有明显的改善。因此,应用i′ap(m)作为预测值的影响可以在仿真中看到,如图(8)所示。仿真参数与实验设置一致,可以看出,补偿效果已经进一步提高。 图8 延时补偿仿真结果 然后,通过改变实验中的速度指令和加载情况,验证了回滞比较器的输出能否保持为1,以及Ued和Ueq估计的正确性。Ued和Ueq的在线估计实验结果如图9所示。 图9 Ued和Ueq在线估计实验结果 在实验中50 ms时,速度命令从2 500 r/min下降到1 000 r/min,Ueq主要部分为空载反电势,其下降趋势与转速基本相同,证明了该方案识别的准确性。可以看到,满载时略大于空载,这是由于满载时电阻电压降较大所致。 对于Ued,d,q轴的耦合项随着速度的减小而减小,因此在两种方案下都更接近于0。在调整过程中,Ued增加是由于当转速降低时,q轴电流基本为负,因此d,q轴耦合项的正负也相应变化。 当给定的速度突然发生变化时,无论是空载还是负载,回滞比较器的输出都会发生变化,从而使系统响应迅速。但是,回滞比较器的输出很快变为1,然后比较器的输出总是为1,这验证了该方案限制电流波动的有效性。 初始参考速度设为2 500 r/min。在0.05 s时,将速度命令降低到1 000 r/min,然后在0.2 s时将速度提高到2 000 r/min。将HCC与传统的FOC方案进行比较,结果如图10所示。 图10 HCC和传统FOC性能比较 根据速度环的机械时间常数和PI参数,两者之间的速度回路性能基本没有差异,所以两种方法的当前参考值基本相同。然而,在抗扰调节时,FOC的电流环路调整时间和超调时间都高于HCC。 还可以看出,HCC的稳态电流波动略大于传统的FOC,空载时波动更严重。一方面,这是由于使用iam2替换ia(m+1)0,两者之间的误差可能导致积分器错误判断,执行错误的积分,从而使当前波动较大;另一方面,采样电路总是有误差,并且空载时的相电流近似等于0,零点漂移问题引起更大的误差,导致更多的错误判断。因此,空载时的电流波动是大于负载的。 在负载突变情况下,将HCC、T-HCC和传统FOC方法的相电流波形进行比较实验,如图11所示,参考速度2 500 r/min。负载突变分两种:空载突变满载和满载突降空载。可以看出,在突然施加载荷时,本文所采用的HCC方法的动态响应过程明显优于传统的FOC方法。当负载突然降低时,虽然FOC电流幅值减小更快,但随后超调更明显。总体来说,恢复稳定状态的时间比HCC要长得多。 图11 负载变化时波形比较 T-HCC在突变负载条件下的性能并不理想,这是因为此时的反电势较高,在一个控制周期中使用0矢量或负矢量引起的转矩下降远远大于正矢量的转矩增加。在速度环PI的影响下,参考电流变化缓慢。因此,在T-HCC方案中,电流总是可以返回到公差区域或大于回滞的上限,使用0和负向量降低了其响应速度。出于同样的原因,也可以看到,当负载突然下降时,T-HCC的响应速度比其他两个HCC的响应速度要快得多。 本文针对PMSM,提出了一种减小HCC电流波动的方法,总结如下: 1) 当实际电流超出滞环时,直接在dq轴上施加较大电压矢量,使电流迅速回到误差带,保持HCC快速性; 2) 当实际电流在误差范围内时,计算输出矢量电压,使得电流保持在滞环内,保持电流稳定性; 3) 考虑到计算输出电压要使用到电机参数,从而提出不连续PI算法得到输出电压,保持HCC鲁棒性; 4) 为了进一步优化该方案,利用数字PWM中心对称输出,提出了一种新的执行延迟补偿策略,该补偿策略可以使PWM期间的补偿时间更加灵活。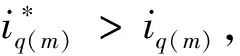
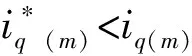
3 延时补偿

4 仿真与实验

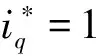

5 结 语
