基于多尺度散布熵的磁声发射信号特征识别方法*
2024-01-25李梦俊沈功田沈永娜
李梦俊,沈功田,沈永娜,王 强
(1.中国计量大学 质量与安全工程学院,浙江 杭州 310018;2.中国特种设备检测研究院,北京 100020;3.国家市场监管无损检测与评价重点实验室,北京 100029)
0 引 言
磁声发射(MAE)[1-2]是指铁磁性金属材料在磁化过程中产生的声发射现象。
在交变磁场激励作用下,材料中磁畴壁发生的不可逆移动、磁化矢量的不可逆转动,以及磁畴壁的产生与湮灭等现象都会产生MAE信号[3-6]。因此,MAE信号对于材料微观组织结构和应力状态非常敏感,在评价铁磁性金属材料的应力集中、弹塑性变形、热处理状态等方面具有广阔的应用前景。
铁磁性材料由于受到应力作用导致内部磁畴结构发生变化,当受到不同应力作用时,激发的MAE信号也不相同。
为了确定MAE信号与材料应力作用的对应关系,王威等人[7]在机理层面讨论了MAE实施应力检测的可能性,并证明了MAE信号的强度受到外磁场和应力变化的共同影响。李志农等人[8]基于有限元仿真与实验,准确描述了静载拉伸和低周疲劳两种状态下Q235钢的MAE信号特性。SU F[9]进行了Q235钢拉伸实验,发现在弹性范围内,无论拉伸应力还是压缩应力,MAE信号强度都以相似的线性方式随应力降低。PIOTROWSKI L等人[10]在平行和垂直压应力作用下,研究了M140-30S GO电工钢试样MAE信号的变化规律,发现材料磁性能受外部和内部应力的共同影响;然而MAE信号幅值较低,在采集过程中容易被噪声干扰,造成部分信息丢失或产生冗余,导致信号特征识别困难。SKALSKYI V等人[11]采用小波变换方法,研究了不同氢化程度结构钢磁化过程中的MAE信号特征。陈炫宇等人[12]在不同的拉伸应力状态下,分析了Q235钢试样MAE信号中样本熵的变化规律。
然而样本熵计算慢、实时性差,且相似性度量易发生突变[13]。散布熵[14]是一种新的时间序列不规则性衡量指标,相较于样本熵受突变信号影响较小,并且考虑了振幅之间的差异性,具有更强的鲁棒性。
由于MAE信号的复杂性,单一尺度的信息熵难以反映其信号特征。变分模态分解(variational mode decomposition,VMD)[15]是一种基于信号频率的变分分析方法。它采用变分约束条件,能够对复杂信号进行从低频到高频的有效分离,实现MAE信号的多尺度化目的。
笔者采用变分模态分解和散布熵,提出一种基于多尺度散布熵的MAE信号特征提取方法;设计并搭建MAE检测实验平台,进行Q345钢静载拉伸实验,并采集0 MPa~400 MPa应力状态下的MAE信号;计算多尺度散布熵,进行特征提取与分类识别,以验证该方法的有效性。
1 磁声发射信号特征提取
1.1 变分模态分解
变分模态分解[16]搜索变分模态最优解,确定模态分量的中心频率和带宽,将不同频段信息的模态分量从信号中分离出来,实现信号的自适应分解的目的。由VMD分解的模态分量uk具有特定的稀疏性质,并且能够重现输入。
VMD变分约束模型为:
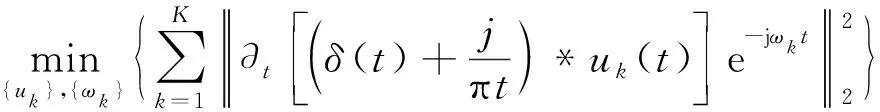
(1)
式中:ωk为uk(t)的中心频率;∂(·)为对时间t求偏导;δ(t)为关于时间t的狄拉克分布;*为卷积算子;-j2=1;f为输入信号。
引入二次惩罚因子α和Lagrange算子λ(t),求解约束变分问题:
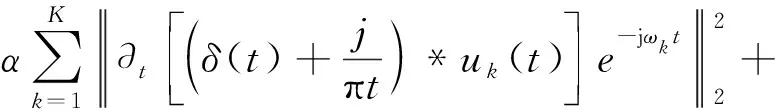
(2)
式中:L(·)为拉格朗日函数;α为带宽平衡参数;λ(t)为关于时间t的拉格朗日乘子项。
1.2 散布熵
散布熵[17]是用于表征时间序列规律性和不规则程度的信息熵算法。散布熵计算步骤如下:
1)利用正态分布函数将长度为N的时间序列x={xj,j=1,2,…,N}映射到y={yj,j=1,2,…,N},yi∈(0,1),即:
(3)
式中:μ为期望;σ2为方差;
2)采用线性变换将y映射到[1,2,…,c]范围内,即:
(4)
式中:round为取整函数;c为类别个数;
3)计算嵌入向量为:
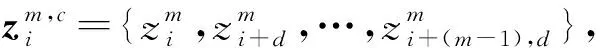
(5)
式中:m为嵌入维数;d为时延;
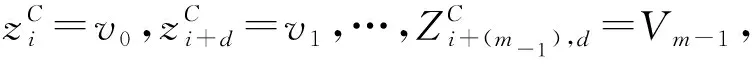
5)计算每种散步模式πv0v1…vm-1的概率:
(6)
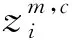
6)根据信息熵的定义,信号x的散布熵定义为:
(7)
1.3 信号特征向量
磁声发射(MAE)信号经过变分模态分解后,每个模态分量含有不同的频段信息,不同应力状态下的MAE信号会引起某些频段分量的变化,对应分量的散布熵值随之改变。因此,信号的散布熵可在一定程度上反映应力特征。需要计算不同模态分量的散布熵值,构成信号特征矩阵,对MAE信号进行特征提取[18]。
MAE信号经过VMD分解后得到n个模态分量[IMF1,IMF2,…,IMFn],计算对应分量的散布熵值[DE1,DE2,…,DEn]作为MAE信号的特征向量。
2 磁声发射信号特征识别分类
支持向量机[19]是基于统计学习理论和结构风险最小化原则的分类算法。它通过引入核函数的方式,将样本数据从低维空间映射到高维空间,在处理非线性问题时可以表现出更好的优势。
笔者将多分类支持向量机应用到磁声发射(MAE)信号特征的识别分类中,把MAE信号的特征向量作为多分类支持向量机模型的输入量,确定最佳的核函数及参数,以进行MAE信号应力特征识别分类。
MAE信号特征提取与分类识别流程如图1所示。
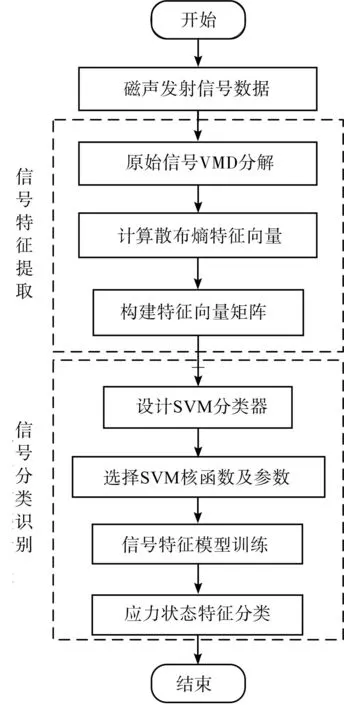
图1 特征提取与分类识别流程 Fig.1 Feature extraction and classification recognition process
笔者对MAE信号特征进行提取与识别分类。其整体流程如下:
1)信号VMD分解。输入MAE信号,采用VMD分解得到n个模态分量;
2)构建特征向量矩阵。计算每个模态分量的散布熵值,进行归一化处理以减小量纲影响,构建信号散布熵特征向量矩阵;
3)确定支持向量机分类模型。建立支持向量机分类器模型,其中核函数选择高斯核函数exp(-γ‖xi-xj‖2);
4)模型训练。将特征向量矩阵随机划分为训练集和测试集,分别使用训练集数据和测试集数据对模型进行训练与测试;
5)应力状态识别。对新的MAE信号进行VMD分解,并计算模态分量散布熵,构建归一化特征向量矩阵,将其输入到支持向量机中,进行信号的分类与识别。
3 实验及结果分析
3.1 实验平台及数据采集
笔者设计搭建了MAE检测实验系统,其系统框图及实物如图2所示。
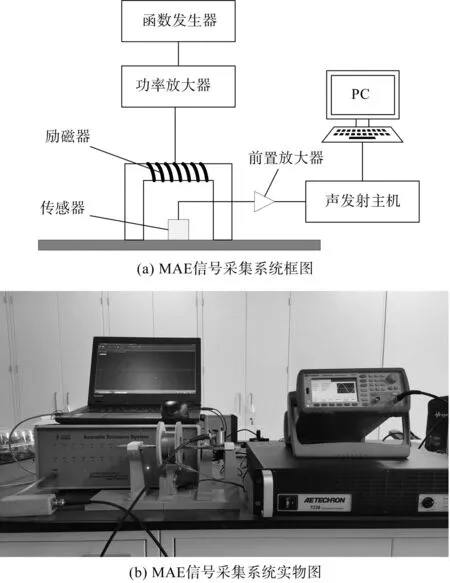
图2 MAE检测实验系统Fig.2 MAE signal acquisition system
采集系统主要包括:声发射检测仪(Soundwel SAEU2S,China),响应频率为1 kHz~2.5 MHz;谐振式传感器(Soundwel SR150,China),频率范围为60 kHz~400 kHz;前置放大器(Soundwel SAEPA2,China);函数发生器(Keysight 33500B,USA),提供线性可调幅值的标准正弦波;功率放大器(AE Techron 7228,USA),提供高保真、低噪声的线性放大信号;励磁器及支架。
MAE信号采集过程为:将传感器放置在实验试件表面,函数发生器产生的励磁信号经过功率放大器线性放大10倍,然后作用于励磁器激励交变磁场;试件在磁化过程中产生MAE信号,传感器采集后经由前置放大器放大,并传输到声发射检测仪,利用计算机进行数据处理。
此处实验选用商用Q345钢作为实验对象,测量不同静载拉伸应力下的MAE信号。
Q345钢拉伸试样尺寸图如图3所示(单位:mm)。
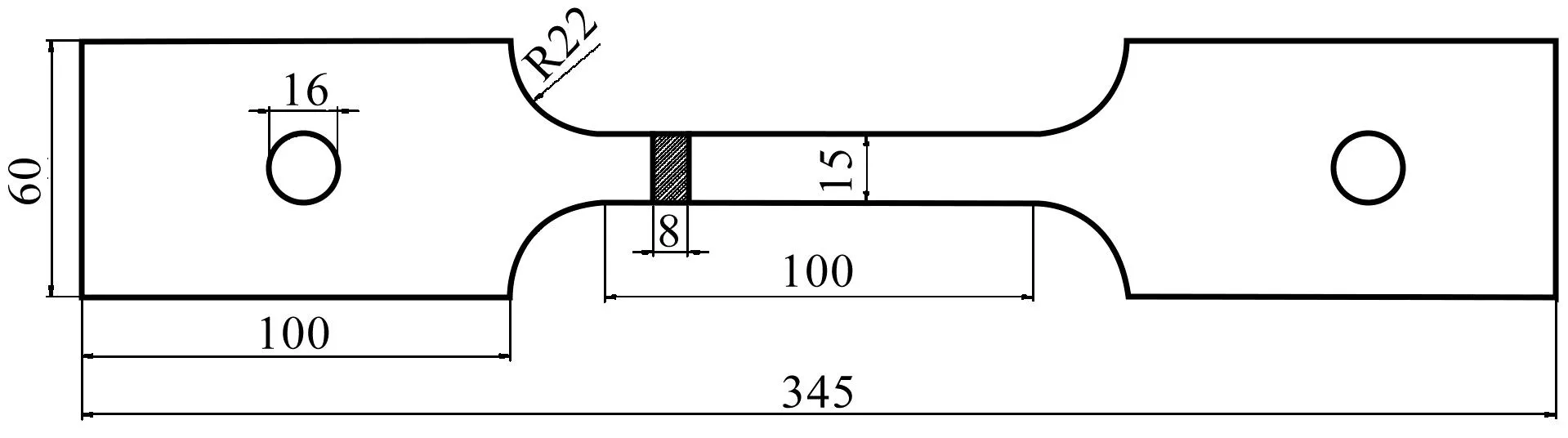
图3 Q345钢拉伸试样尺寸图Fig.3 Dimensional diagram of Q345 steel tensile specimen
笔者采用深圳新三思CMT5504/50 kN微机控制电子万能试验机进行Q345钢拉伸试样的拉伸实验。
静载拉伸实验图如图4所示。

图4 Q345钢试样静载拉伸实验图 Fig.4 Statictensile test graph of Q345 steel specimen
实验加载方式为夹头位移速率恒定加载,加载速率为0.5 mm/min。当加载应力达到80 MPa、160 MPa、240 MPa、320 MPa、400 MPa等应力值时,停止加载,并进行MAE信号采集(MAE信号采集传感器和励磁器布置方式见图4)。
笔者设置励磁信号为频率50 Hz,幅值1 V的正弦波。励磁波形如图5所示。
图5 励磁信号波形Fig.5 Excitation signal waveform
磁声发射信号的采样频率设置为1 MHz,每种应力状态各采集60个数据段,每组数据有10 000个采样点,构成MAE信号原始样本数据集,用于分析。
MAE信号的时频域如图6所示。
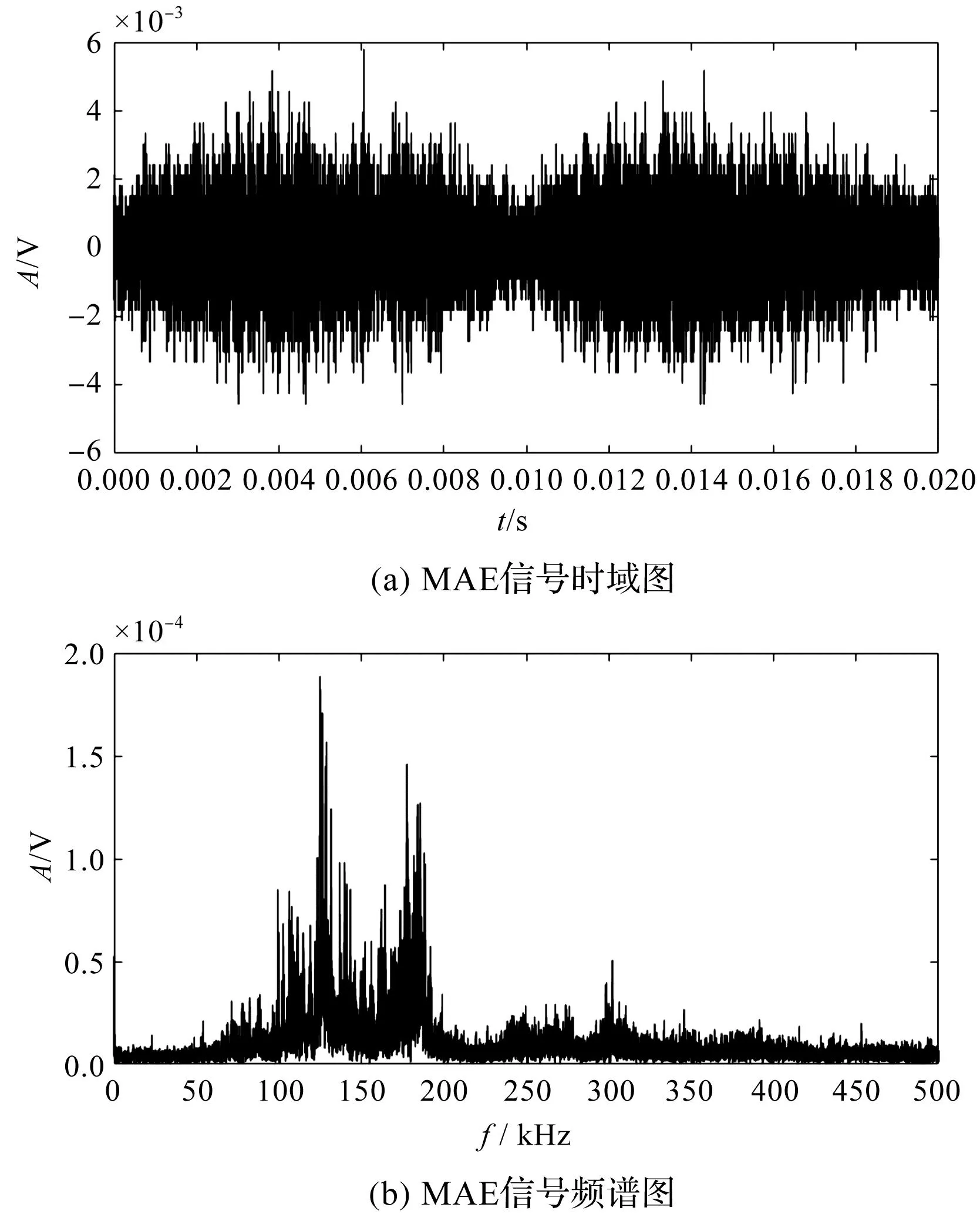
图6 MAE信号时频图Fig.6 MAE signal time-frequency diagram
由图6(a)可知:MAE信号为单峰纺锤形或者双峰驼峰形包络信号,具有周期性;励磁周期是MAE信号周期的2倍,即一个交变磁场变化周期内产生2个信号幅值、包络形状相似的MAE信号。
由图6(b)可知:MAE信号的频谱范围主要分布在20 kHz~500 kHz之间,其中有2个主峰峰值分别位于130 kHz和185 kHz附近。
3.2 数据分析
笔者用VMD对MAE信号样本数据集进行分解(VMD运行前需要预设分解模态层数K),采用波形法比较不同分解层数后的模态分量,根据对比不同层数模态分量的最大中心频率,确定最优分解层数K为6,并对采集的MAE信号进行最优层数的变分模态分解。
笔者对MAE信号进行VMD分解,得到了各分量波形图,如图7所示。
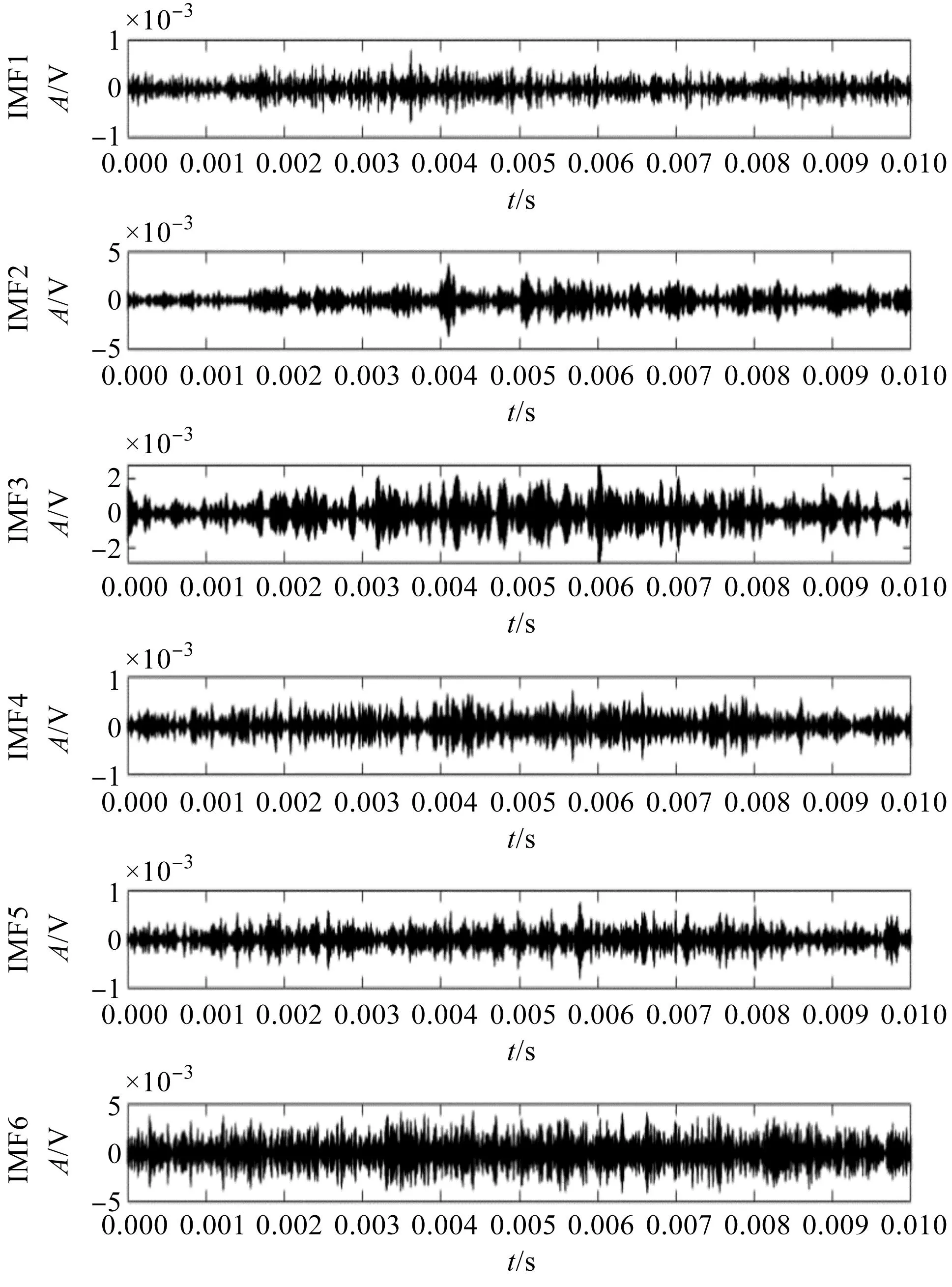
图7 MAE信号分解各分量波形图 Fig.7 MAE signal decomposition waveform diagram of each component
笔者对MAE信号进行VMD分解,得到各分量频谱图如图8所示。
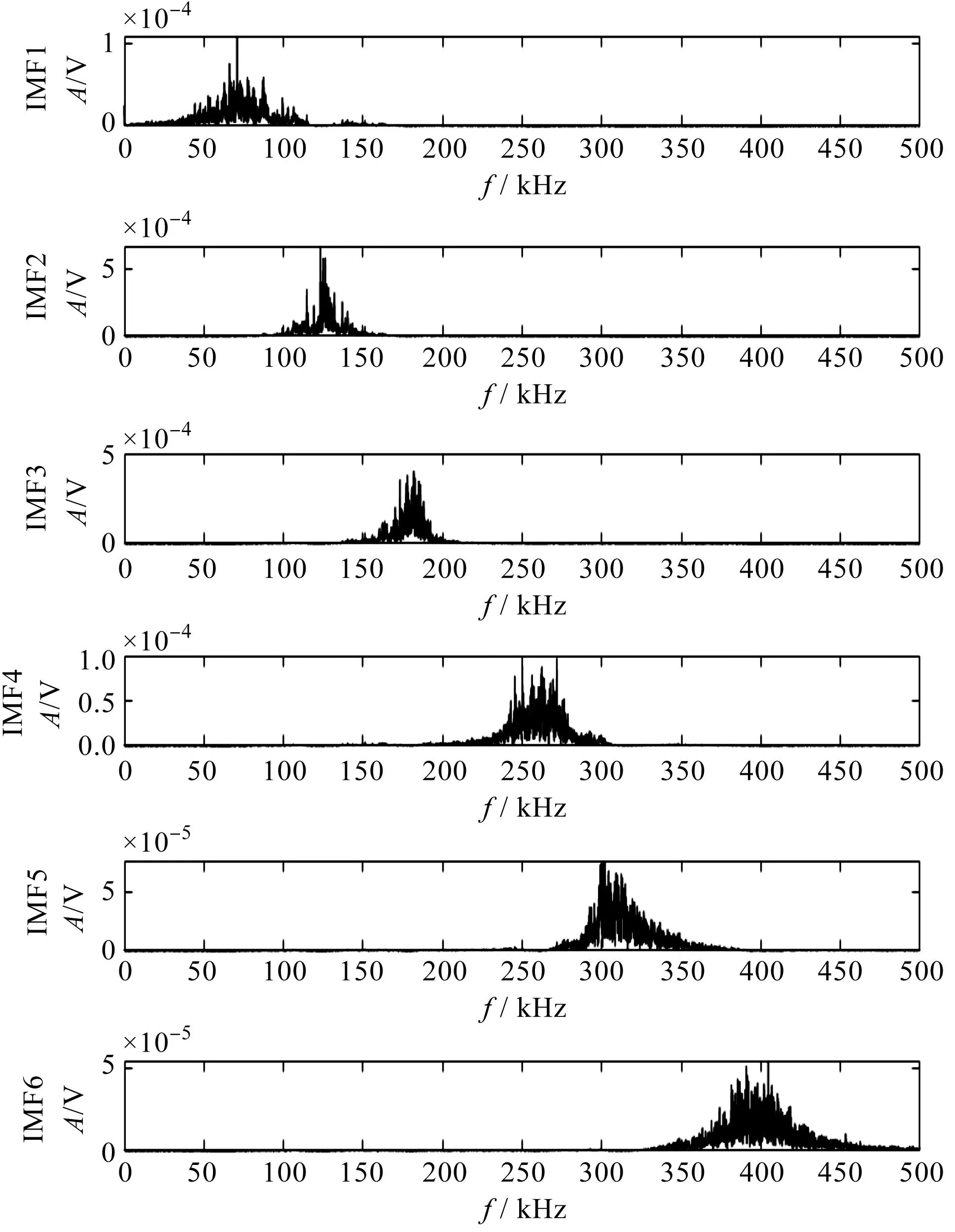
图8 MAE信号分解各分量频谱图Fig.8 MAE signal decomposition spectrum of each component
由图7和图8可知:采用变分模态分解将MAE信号从低频到高频相互分离成不同信号频段,其中第1个IMF分量的频率带宽为0 kHz~125 kHz,中心频率为72 kHz;第2个IMF分量的频率带宽为98 kHz~160 kHz,中心频率为125 kHz;第3个IMF分量的频率带宽为140 kHz~220 kHz,中心频率为185 kHz;第4个IMF分量的频率带宽为200 kHz~310 kHz,中心频率为275 kHz;第5个IMF分量的频率带宽为240 kHz~380 kHz,中心频率为300 kHz;第6个IMF分量的频率带宽为340 kHz~500 kHz,中心频率为400 kHz。
由此可知,采用VMD能够将MAE信号和背景噪声分离。其中,前3个IMF分量的频率带宽较小,信号幅值较高,主要包含MAE信号的有效信息;其余分量频率带宽较大,并且存在大量幅值较低的背景噪声。
但是,每个分量都包含不同的信号特征,不能摒弃,因此,需要计算不同信息频段的散布熵值,多尺度反映MAE信号的特征信息。
实验共设置Q345钢承受静载拉伸应力0 MPa~400 MPa六种状态,每种状态采集60组MAE信号样本数据,每组样本数据有6个特征值,共构成360×6维的特征矩阵。
在每种应力状态下,笔者随机选择了3组MAE信号特征向量列出,如表1所示。
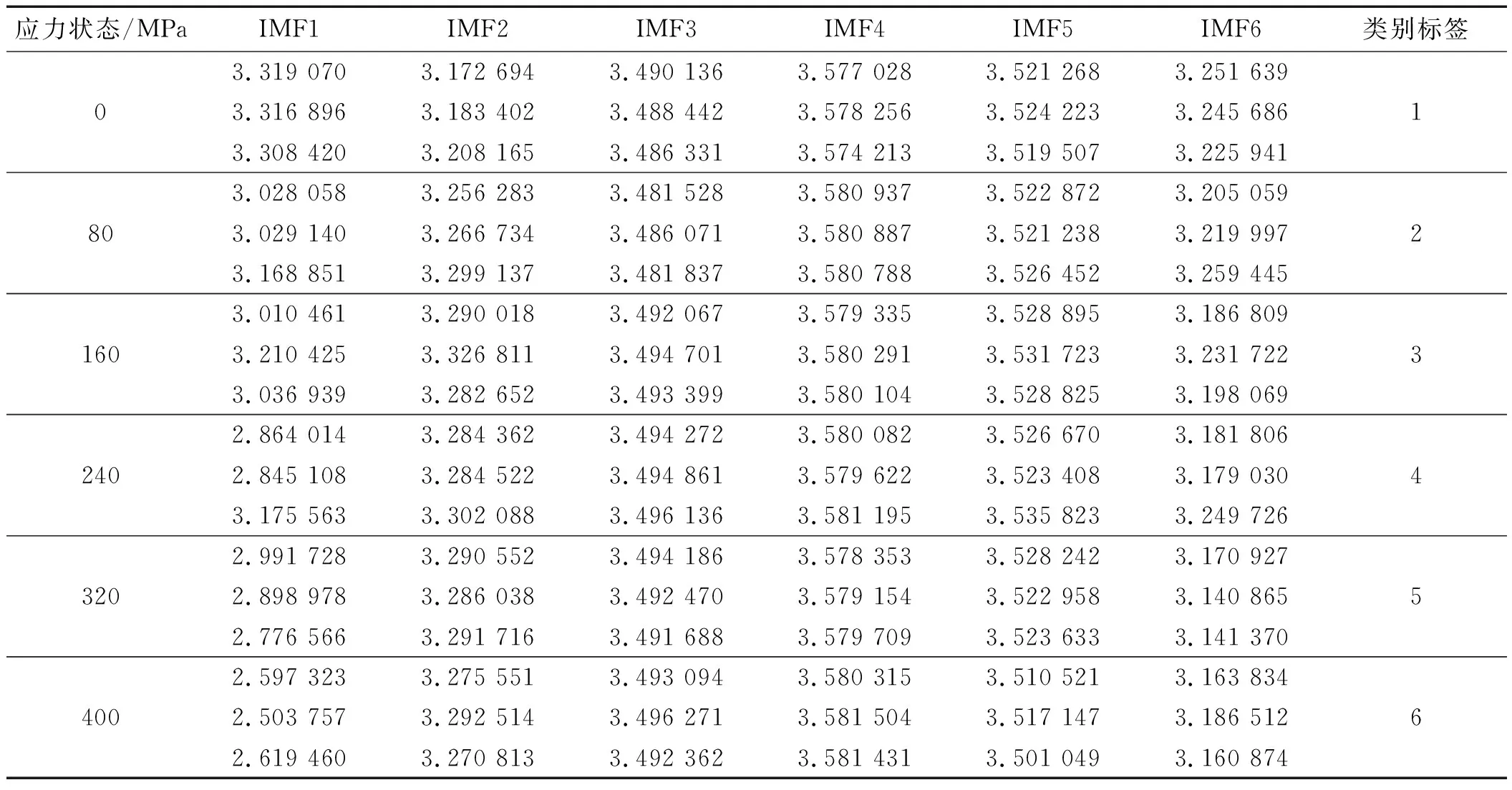
表1 Q345钢不同应力状态MAE信号的部分特征向量Table 1 Partial characteristic vectors of MAE signals under different stress states for Q345 steel
根据不同应力状态,笔者分别设置类别标签为1~6,用于多分类支持向量机识别分类模型;从特征向量矩阵中随机选取70%的样本数据,用来训练多分类支持向量机模型,把剩余30%的样本数据作为测试样本。
笔者把MAE信号特征向量矩阵输入支持向量机中,进行MAE信号特征状态识别分类,测得整体分类准确率为95.370 4%。
笔者对MAE信号特征向量矩阵进行支持向量机分类,其结果如图9所示。
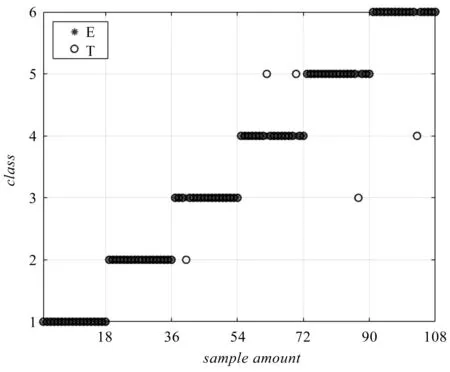
图9 MAE信号的应力特征分类结果Fig.9 Stress characteristic classification results of MAE signal注:E为期望输出;T为真实输出。
由图9可知:在不同的应力状态下,有5个样本数据分类错误,且主要集中在应力较大的情况下。这是因为随着拉伸应力的增加,材料磁畴结构的改变会使得MAE信号特征不明显。
但是分析上述整体结果可知:多尺度散布熵能够较好地表征MAE信号的特征信息,证明了将多尺度散布熵与支持向量机相结合,用于MAE信号特征识别这种方法是有效的。
4 结束语
针对MAE信号易受噪声影响的问题,笔者提出了一种基于多尺度散布熵的MAE信号特征识别方法,并采用该方法对Q345钢进行了静载拉伸实验,并采集了不同应力状态下的MAE信号,进行了多尺度散布熵的特征提取与识别分类。
研究结论如下:
1)利用VMD对MAE信号进行了分解,可以有效减少噪声对MAE信号的影响,并且避免信号分解中出现模态混叠等现象;针对MAE信号的复杂性,分别计算了不同模态分量的散布熵值,可多尺度地提取MAE信号的特征信息;
2)建立基于多尺度散布熵的支持向量机分类模型,输入Q345钢在0 MPa~400 MPa应力状态下的MAE信号数据,对模型进行了测试,准确率达到95.370 4%,证明了将多尺度散布熵与支持向量机相结合用于MAE信号特征识别的方法是有效的。
在后续的工作中,笔者将进一步降低MAE信号中的噪声,并针对散布熵的计算开展研究,以提高基于多尺度散布熵的MAE信号特征识别方法的特征识别效率和精度。
