基于贝叶斯优化的GRU网络轴承剩余使用寿命预测方法*

孟琳书,张音旋,张 起,王 豪

(1.中国航空工业集团公司 沈阳飞机设计研究所,辽宁 沈阳 110035;2.先进科技(中国)有限公司,四川 成都 610000)

0 引 言

滚动轴承是旋转机械中重要且相对易失效的基础零部件[1],其由于磨损、疲劳等原因而产生的性能退化或故障将影响设备的正常工作,甚至会造成财产损失和人员伤亡等一系列后果[2]。

因此,预测滚动轴承可能的失效时刻,并根据预测结果提前对设备进行预测性维护是十分必要的,可以避免由于滚动轴承失效而造成的设备停机[3]。

预测滚动轴承剩余使用寿命从而进行设备健康管理已经成为机械故障诊断领域的研究热点之一[4]。总体上,滚动轴承寿命预测方法可以分为3类:基于物理模型的方法、基于数据驱动的方法和混合方法[5]。由于具备良好的泛化性能,数据驱动方法中的基于深度学习的预测方法受到了广泛的关注,已经成为滚动轴承剩余使用寿命预测的重要手段之一[6]。

近年来,深度学习中的时间序列模型在滚动轴承寿命预测领域得到了广泛应用。

CAO Y等人[7]采用了一种基于残差注意力的时间卷积网络模型来预测滚动轴承的剩余使用寿命;但该模型对多工况轴承的跨工况预测能力不足。WANG B等人[8]引入可分离卷积和压缩-激励单元,实现了端到端的滚动轴承剩余使用寿命预测目的;但受限于隐式特征难以结合工程经验问题,导致其通用性欠佳。GUO R等人[9]采用了一种结合经验模态分解和长短期记忆(long-short term memory, LSTM)网络的剩余使用寿命预测方法,学习固有模态函数和滚动轴承剩余使用寿命之间的映射关系;但该方法的长期寿命预测能力不足。

上述学者针对不同使用场景结合多种深度学习模型开展了滚动轴承寿命预测,并取得了一定进展;但预测模型的超参数大部分由研究人员根据经验手动进行选择调优,这种选择方法显著降低了模型优化效率。因此,有学者开发了贝叶斯优化、Successive Halving和Hyperband等超参数调节方法。其中,贝叶斯优化基于贝叶斯定理估计目标函数的后验概率分布,依据后验分布对超参数组合进行采样,并根据采样结果不断完善后验分布的形状,从而高效地找到目标函数的全局相对最优解,在深度学习模型的超参数调节中得到了广泛应用。

笔者提出一种基于注意力GRU模型与贝叶斯优化的滚动轴承剩余使用寿命预测方法。

首先,使用小波包分解重构对原始振动信号进行降噪处理;其次,在去噪后的信号上提取时域特征;然后,将时域特征输入GRU模型中挖掘输入特征与剩余寿命的映射关系;最后,利用贝叶斯优化方法对模型的超参数进行搜索调整。

1 特征提取与优化筛选

振动信号采集方便且蕴含着丰富的退化信息,是滚动轴承失效分析的常用信号。该领域内积累了众多研究人员的先验知识,产生了时域、频域和时频域等一系列特征计算方法。不同人工特征对各种故障类型的敏感程度有一定差异且数据质量不同,因此需要对特征进行优化筛选。此外,由于采集过程中噪声影响难以忽略,对振动信号进行降噪是取得一个良好预测结果的必要条件。

笔者使用小波包分解重构进行信号降噪。该方法采用一组正交的小波基函数将原始信号分解为高频分量和低频分量,然后将得到的高频分量和低频分量作为新一轮输入信号继续进行迭代分解。通过调整小波基函数的尺度和平移参数,可获得信号分量的频率信息与时间信息。

由于传感器采集的振动信号为离散数据,因此在使用小波包变换时,一般采用离散小波变换。

其过程表示如下:

(1)

式中:f(t)为原始信号;φ()为小波函数;φ*()为小波函数的共轭函数;a为通过伸缩控制小波频率的尺度参数;b为平移参数,该参数使频率分量具有时间信息。

特征提取在寿命预测领域具有重要地位,对模型的最终表现影响巨大。一个良好的特征应具有单调性、趋势性和鲁棒性等性质。传统的人工经验特征趋势性和单调性较差,不利于模型预测。

考虑到轴承的退化是一个损伤累积过程,因此笔者对其特征与趋势的累加进行缩放,并滤除特征中的噪声,降低噪声对累积计算过程的影响,以实现特征优化目的[10]。

2 注意力GRU模型

2.1 GRU单元

循环神经网络具备独特的递归结构和内部神经元的参数共享机制,使其可以学习时间序列之间的依赖关系,但其存在梯度消失问题,即梯度被近距离梯度主导,导致模型难以学到远距离的依赖关系。

GRU[11]是循环神经网络(recurrent neural network, RNN)的一种变体,其通过添加“门”结构调节信息流,以及“记忆细胞”存储长期信息,可有效克服短期记忆的缺陷,缓解梯度消失问题。

GRU中包含重置门和更新门。重置门是根据上一时间步的隐藏状态和当前输入,控制历史信息的遗忘程度。

重置门表示如下:

rt=σ(Wr×[ht-1,xt])

(2)

式中:Wr为重置门中的权重矩阵;ht-1为上一时间步的隐藏状态;xt为当前时间步的输入。

更新门控制传递到当前时间步的新信息。

更新门表示如下:

zt=σ(Wz×[ht-1,xt])

(3)

式中:Wz为更新门中的权重矩阵。

笔者结合重置门和更新门中的信息,计算当前时间步的隐藏状态,隐藏状态表示如下:

(4)

相较于单向GRU网络,双向GRU网络可以利用当前时间步的未来信息得到当前时间步的预测值,即使用来自当前时间步两端的序列信息来预测输出。

对于时间序列预测任务,上述特性意味着在预测任意时间步的输出时,网络已经将完整的输入序列信息纳入计算过程,而非如单向GRU网络一样只考虑过去的信息,这有助于网络更好地理解时间步之间的依赖关系。

2.2 基于注意力机制的Encoder-Decoder结构

注意力机制[12]源于人类的行为,其给予时间序列中关键时间步较高权值,使模型更关注对输出结果影响较大的时间步,而忽略那些对输出结果几乎无影响的时间步。

上述机制提高了模型的信息处理能力,便于捕捉轴承退化特征的长期趋势,常与Encoder-Decoder结构的神经网络配合使用。

注意力机制计算方法多样,但本质上是计算并分配权重的过程。其分配过程表示如下:

Score=fatten(he,hd)

(5)

(6)

(7)

(8)

式中:he为编码器所有时间步上的输出;hd为编码器当前时间步上的隐藏状态;α为注意力权重矩阵。

在权重计算过程中,首先,笔者将编码器所有时间步上的输出和解码器当前时间步上的隐藏状态点乘,计算两者之间的相似度,相似度越大,分数值(Score)越大;其次,对Score值进行归一化处理,得到注意力权重矩阵α;然后,将注意力权重矩阵与编码器输出矩阵相乘,得到输出C;最后,将上一步的输出C与当前时间步上的原本输出拼接后进行线性变换,以得到当前时间步上的最终预测值。

2.3 贝叶斯优化

神经网络的超参数对模型表现起着决定性作用。目前,在寿命预测领域,大多数网络模型依然采用手动调参的方法。该方法依赖个人经验、效率较低,往往得不到最优的超参数组合。

笔者利用贝叶斯优化方法搜索模型的高维超参数空间。

贝叶斯优化的核心主要包括代理模型和采集函数两部分。代理模型用于拟合真实目标函数的先验分布,常用的模型有高斯过程、Parzen树估计(tree Parzenes-timator,TPE)等。

采集函数通过权衡“开发”和“探索”之间的关系来指导下一次迭代的采样点选择,以实现代理模型的最大拟合。采集函数能够直接决定模型优化的性能,影响优化过程的收敛速度及后验分布的拟合效果。常用的函数包括“期望提升”“置信限准则”和“概率提升”等。

笔者选择TPE作为代理模型,“期望提升”函数作为采集函数。

3 剩余使用寿命预测流程

基于注意力GRU模型的剩余使用寿命预测算法具体流程如图1所示。

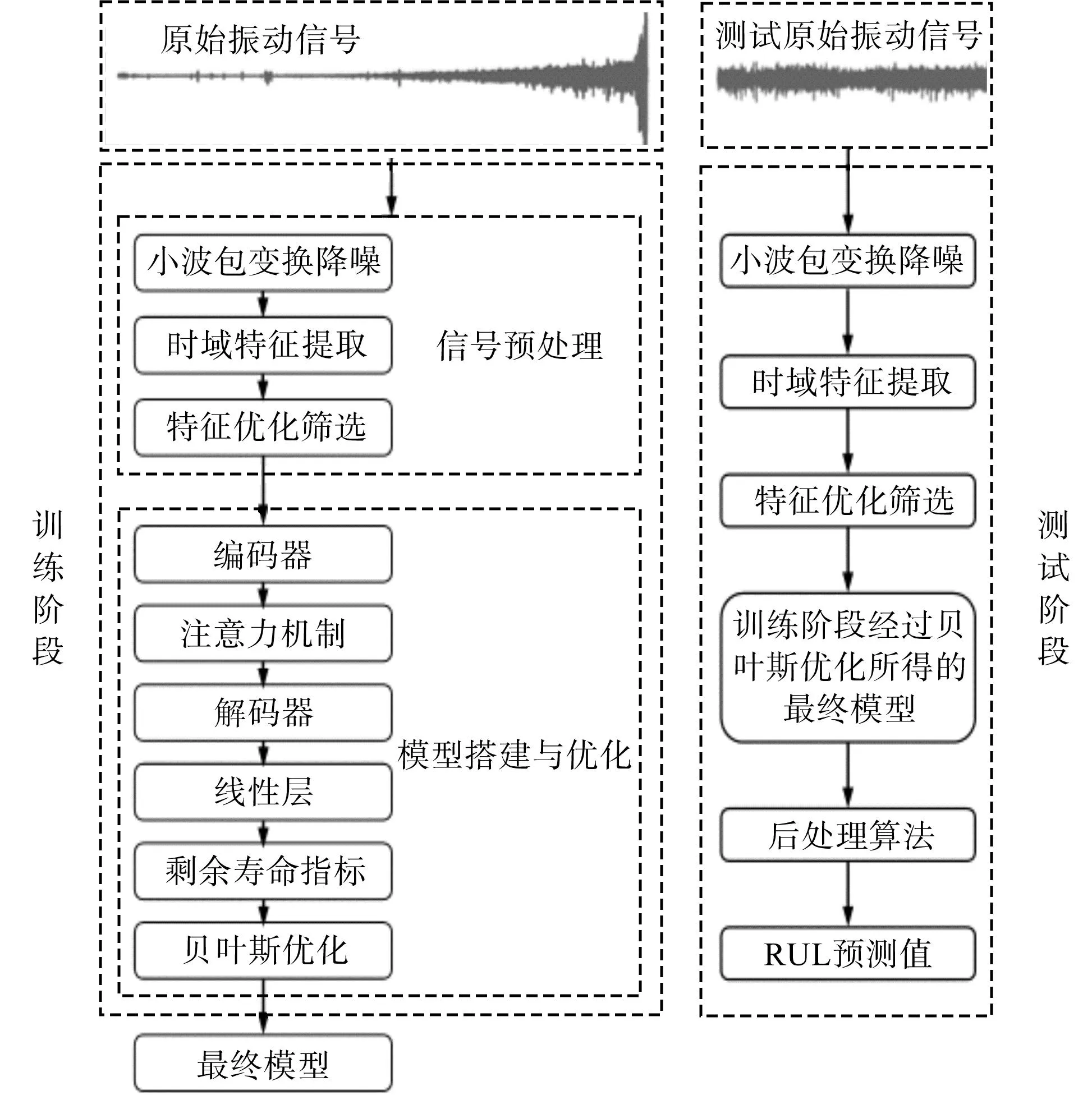
图1 预测流程Fig.1 Forecasting process

流程主要分为小波包变换降噪、时域特征提取、特征优化与筛选、模型搭建、模型训练及优化、模型测试等主要步骤:

1)小波包变换降噪。原始振动信号经过小波包分解(小波基函数为db4),根据信号的通用阈值采用软硬阈值折中的方式处理分解后的细节系数,将处理后的细节系数进行重构,以得到最终降噪后的信号;

2)时域特征提取、优化及筛选。时域特征具有直观、计算简单、趋势明显的优点,能够表征轴承运行状况的一部分信息。计算时域特征后使用Savitzky-Golay滤波器进行滤波,对滤波结果进行优化并筛选获得最终输入到模型的特征;

3)模型搭建、训练及优化、测试。搭建注意力GRU模型的同时,将网络的层数、GRU单元的偏置等网络参数作为贝叶斯优化的超参数,并将学习率、序列长度、dropout等参数作为优化变量,利用贝叶斯优化方法对模型进行训练,得到最优模型,并在测试数据上测试所得模型。

预测流程的实际运行效果如图2所示。

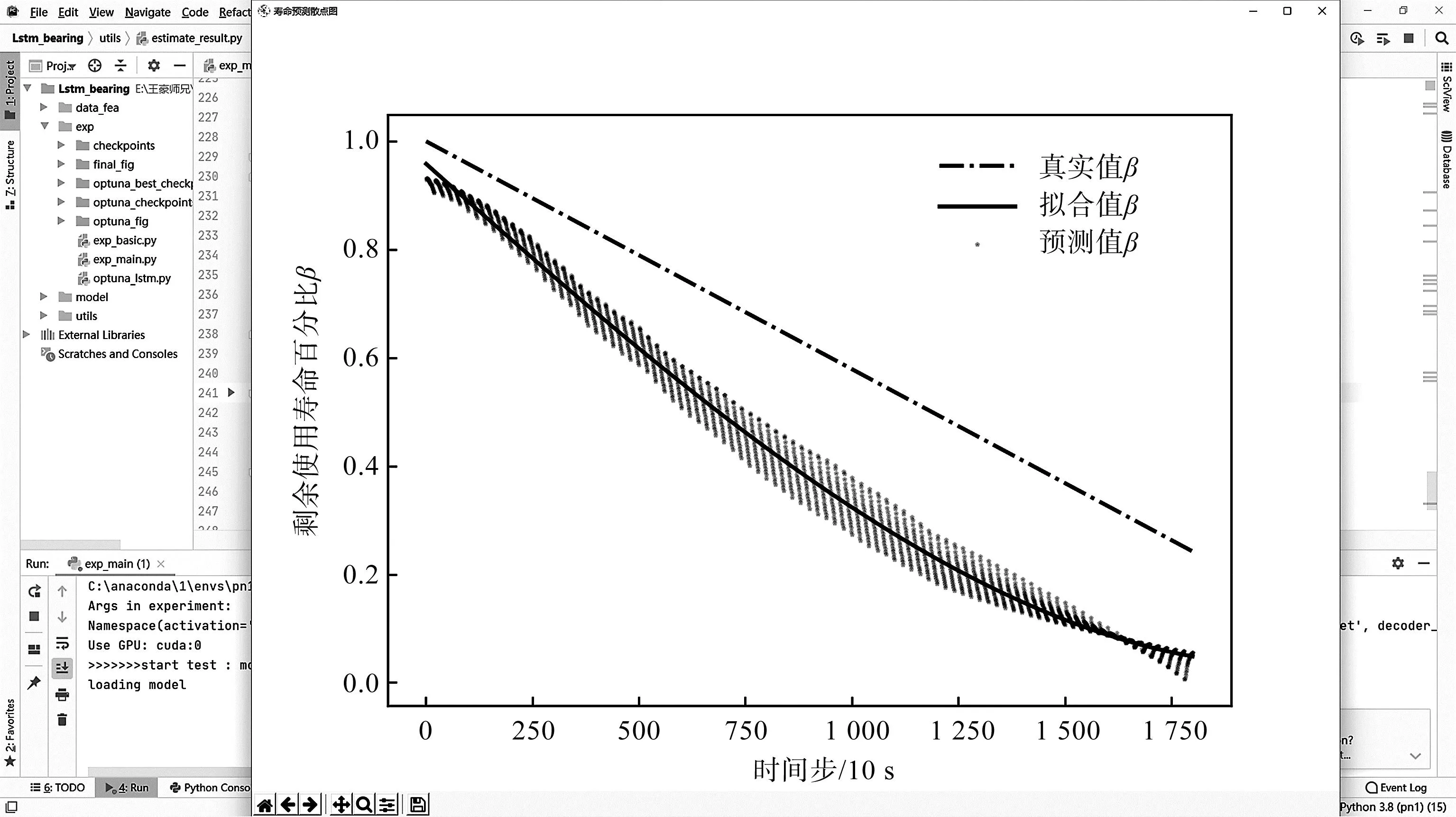
图2 预测流程运行效果Fig.2 Forecasting process in action

4 实验验证与结果分析

4.1 实验数据

此处笔者使用的数据来自于IEEE PHM2012[13]挑战赛,其数据集中包含6个全生命周期的训练数据和11个截断的测试数据。

数据集具体情况如表1所示。

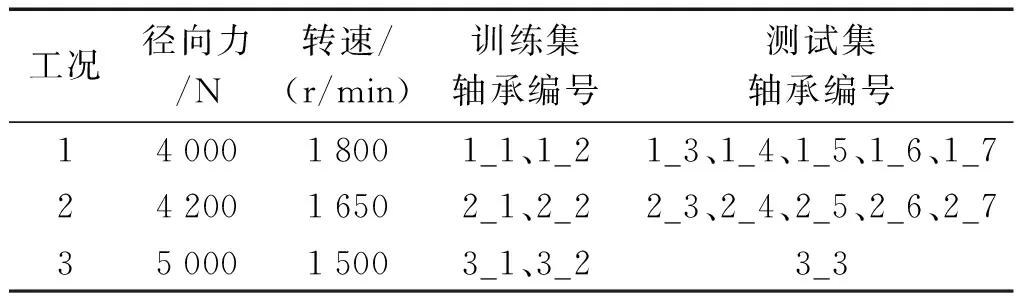
表1 轴承数据集Table 1 Bearing data set

笔者在每个轴承上采集了水平和垂直方向上的振动信号。根据SINGLETON R K等人[14]的研究结果,相较于水平振动信号,垂直振动信号所包含的有用退化信息很少。因此,笔者最终使用轴承水平方向上的振动信号,在工况1的7个数据上进行实验验证。

4.2 评价指标

在实际生产中相较于滞后预测(寿命预测值大于真实值),超前预测(寿命预测值小于真实值)更有价值,其可以提供正确的维修决策信息。

为准确评估模型的性能和实际表现,PHM 2012挑战赛给出了标准得分函数,其对超前预测和滞后预测施加了不同程度的惩罚,惩罚表示如下:

(9)

式中:Ei为轴承剩余寿命真实值与预测值之间的误差;Ai为最终得分。

4.3 时域特征提取、优化及筛选

笔者根据文献[15],选取标准差、反正切标准差、均方根、峰峰值、偏度、峭度、峰值因数、裕度因数、波形因数、脉冲因数、偏度因数、峭度因数和上限等特征,绘制时域波形,并根据特征计算公式去除冗余波形与相近特征。

时域特征选择如表2所示。

表2 时域特征Table 2 Time domain feature

笔者使用趋势累积方法对提取到的特征进行优化,并利用单调性、趋势性、鲁棒性指标评估筛选特征。

时域特征优化前后的评估指标对比如表3所示。

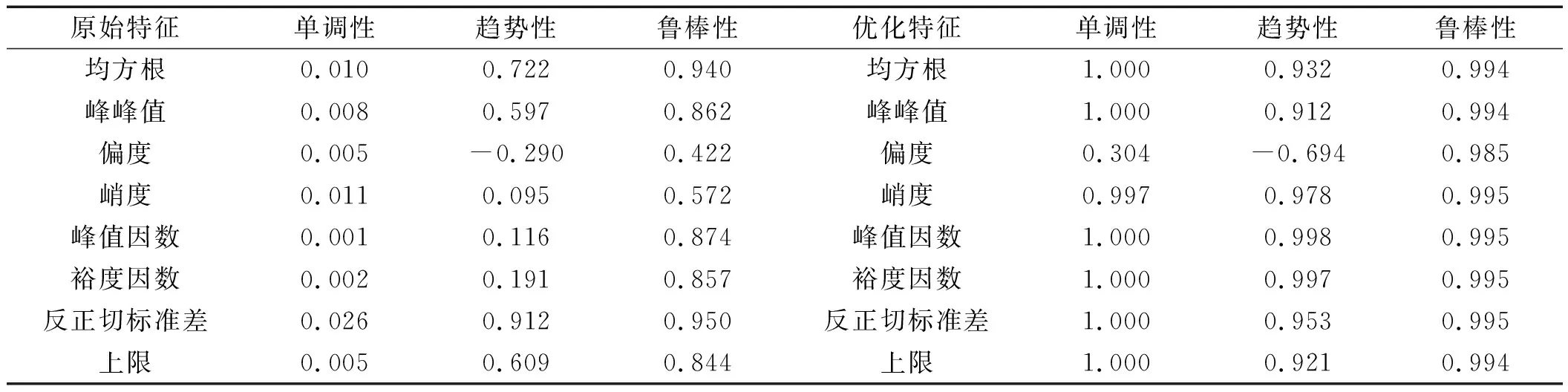
表3 特征优化评估Table 3 Feature optimization evaluation

由表3可得出:趋势累积方法可以有效优化特征的单调性、趋势性和鲁棒性。

根据优化后的3个指标对时域特征进行筛选,最终输入模型的时域特征为均方根、峰峰值、峭度、峰值因数、裕度因数、反正切标准差和上限。

4.4 实验结果

笔者使用python(3.8.10)完成所有数据处理及模型搭建工作。其中,深度学习框架为pytorch(1.9.0),cuda版本为11.3。全部实验均在搭载NVIDIA 3060 GPU,Intel i5-10400F CPU的Windows10 64位操作系统计算机上完成。

首先,确定影响GRU网络性能的超参数及其对应范围,形成超参数域空间。在域空间中随机初始化超参数组合,并以此搭建待训练的网络模型。以退化特征集为输入,剩余使用寿命标签为输出,对网络模型进行训练。将测试数据输入到训练好的网络模型中,计算预测剩余使用寿命的均方根误差,并将其作为优化目标值,构建由超参数和目标值组成的TPE代理模型。利用采集函数在域空间中迭代采样,并根据采样结果更新代理模型,直到目标值收敛。其中,所确定的GRU网络模型使目标值最小的超参数组合,其即为最优模型。

超参数选择如表4所示。

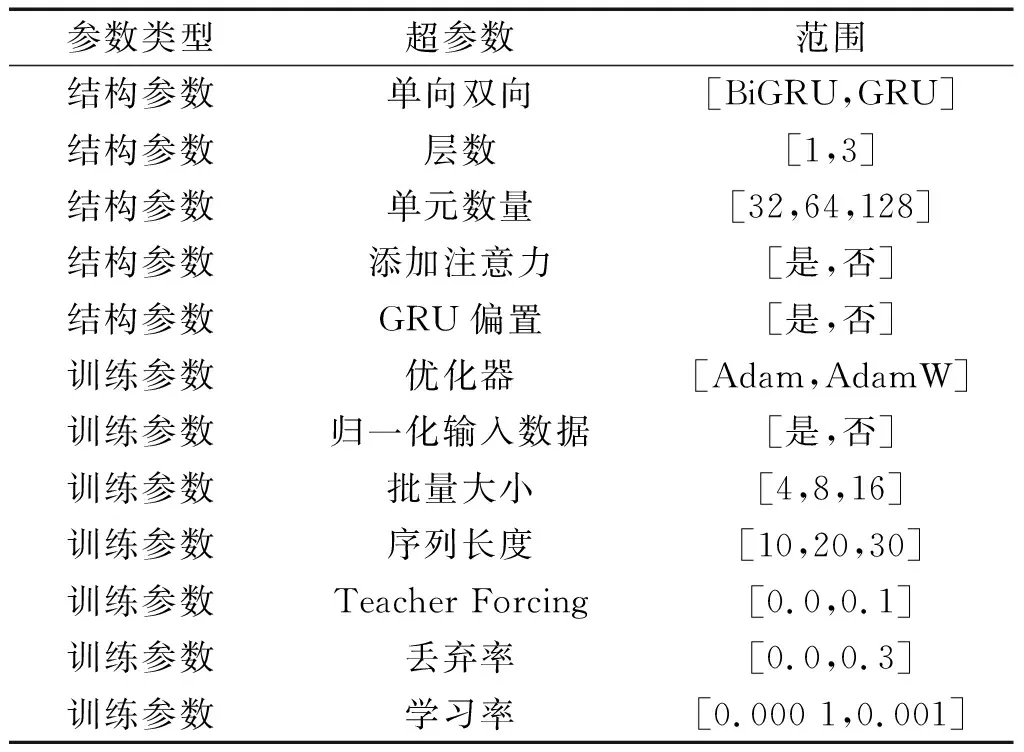
表4 超参数空间Table 4 Hyperparameter space

在巨大的超参数空间中,笔者仅抽样200组超参数进行训练优化,经过贝叶斯优化后得到的参数组合为(BiGRU,1,32,否,是,AdamW,是,4,20,0.0,0.05,0.000 1),在该参数组合下测试所得到的模型。

轴承1_5、1_6预测结果如图3所示。

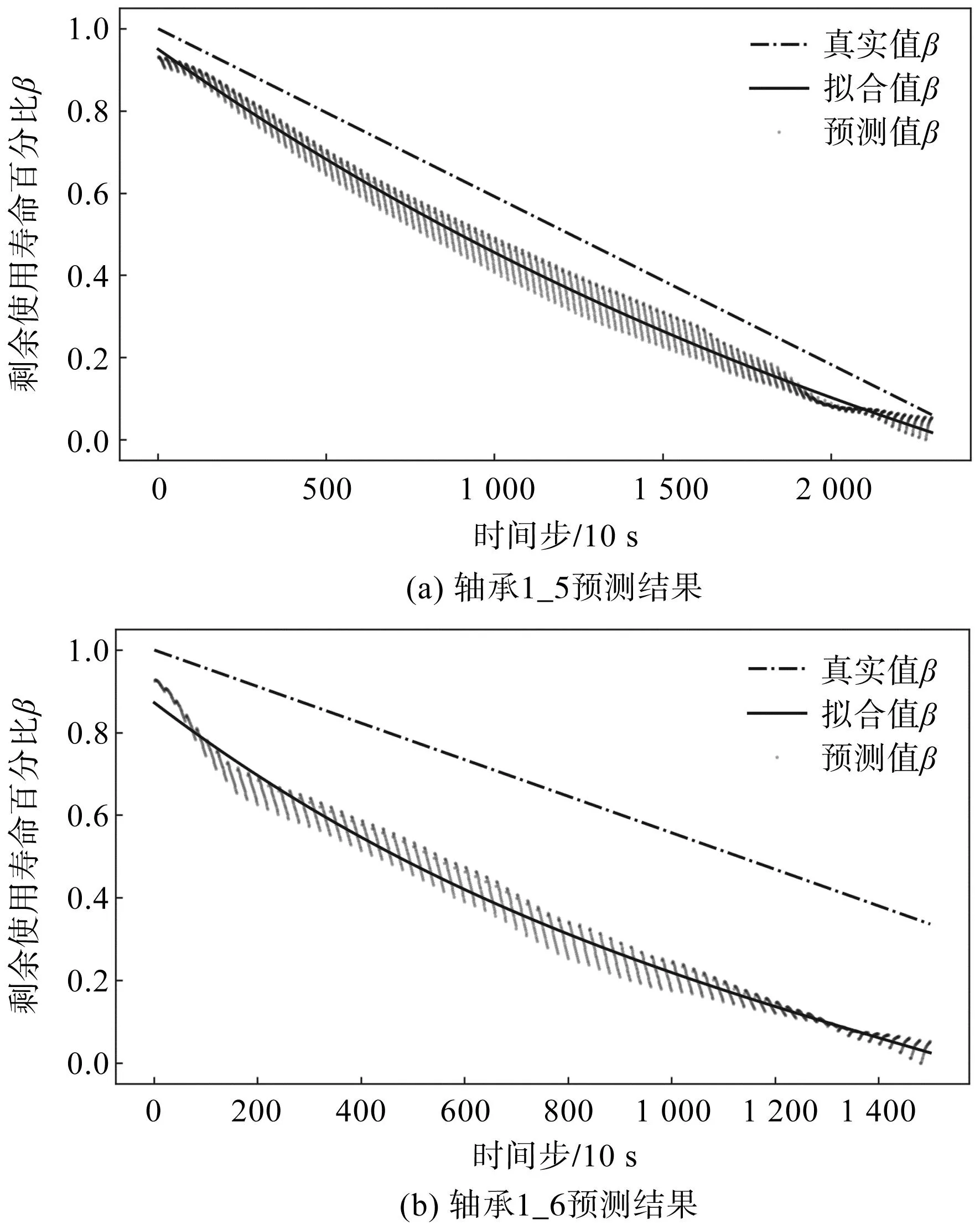
图3 轴承寿命预测结果Fig.3 Life prediction results of bearings

粗虚线为轴承的真实剩余使用寿命百分比;黑色实线为三次多项式拟合值;黑色点构成的斜划线为模型的预测值;其中三次多项式的拟合值可以作为轴承退化趋势的参考。

为了证明基于贝叶斯优化的GRU网络的有效性,笔者将实验结果与其他文献中的3种方法(卷积LSTM[16]、自注意LSTM[17]、RNN[18])的预测结果进行了对比。

基于贝叶斯优化的GRU网络与其他文献的对比结果如表5所示。

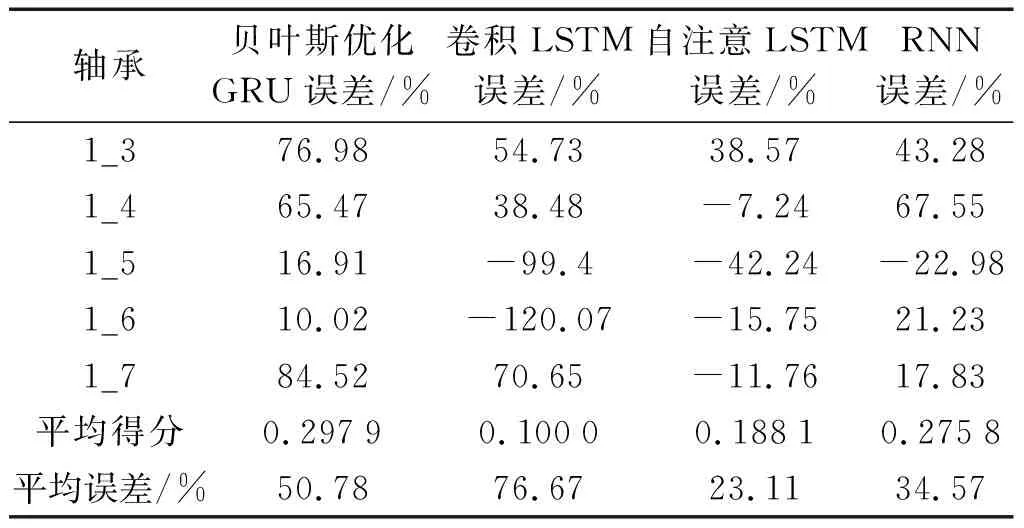
表5 基于贝叶斯优化的GRU网络与其他文献方法的结果对比Table 5 The results of the GRU network based on Bayesian optimization are compared with those of other literatures

由表5可以看出:基于贝叶斯优化的GRU网络平均得分高于另外3个文献中方法的得分结果,且平均预测误差有所降低。基于贝叶斯优化的GRU网络对于真实寿命较短的轴承预测结果较为准确,而对于真实寿命较长的轴承预测误差较大,但并没有出现预测值大于真实值的情况,其可以作为轴承临近失效阶段的剩余使用寿命参考。

上述结果证明了基于贝叶斯优化的GRU网络的有效性。

5 结束语

传统的滚动轴承剩余使用寿命预测模型存在参数优化的困难。针对这一问题,笔者提出了一种基于贝叶斯优化的GRU网络滚动轴承剩余使用寿命预测方法,并进行了实验验证,即以PHM2012数据集为例,结合贝叶斯优化算法对基于Encoder-Decoder结构的门控循环单元(GRU)预测模型的多个超参数进行了优化。

研究结论如下:

1)趋势累积方法对由振动信号所提取出的时域特征的单调性、趋势性和鲁棒性具有明显的优化效果;

2)基于注意力的GRU模型可以用于有效地预测滚动轴承的剩余使用寿命,且平均得分相较于其他3种方法的最优值提高了8.01%;

3)采用贝叶斯优化方法能够在较短的时间内通过采样训练得到较优的预测结果,避免了繁琐的人工调参和网格搜索的巨大时间代价。

目前,基于注意力的GRU模型的预测精度还有待进一步提高,且其对剩余寿命较长的轴承预测精度仍然较低。因此,在后续的研究中,笔者拟采用迁移学习等方法进一步提高滚动轴承寿命预测模型的泛化性能。