基于MOBWO-MCKD的风机滚动轴承故障特征提取方法*

霍忠堂,高建松,张丁丁

(邯郸学院 机电学院,河北 邯郸 056000)

0 引 言

传感器技术的发展,使得状态监测及故障诊断在维护机械安全、稳定方面起到了日益重要的作用[1]。

作为风力发电机的关键零部件,滚动轴承的运行状态会影响机组的运行稳定[2]。由于风力发电机运行工况复杂多变,导致发电机轴承承受交变载荷时会不可避免地发生点蚀、磨损、电腐蚀等故障。同时,轴承的更换成本也较高[3-4]。因此,对发电机轴承进行有效故障诊断,及时发现故障并进行维修,对于保证机组正常稳定运行,延长轴承使用寿命等方面具有重要意义[5]。

振动信号易采集,且包含较多有用的特征信息,因此轴承故障诊断通常基于振动信号[6]。传统的故障诊断方法有傅里叶变换[7]、变分模态分解[8]、包络谱[9]等。韩朋朋等人[10]提出了遗传算法优化变分模态分解(variational mode decomposition, VMD)与增强包络谱的轴承故障诊断方法,利用遗传算法对VMD进行了参数寻优,获取了最优模态分量和惩罚因子,达到了轴承故障诊断的目的。JALAYER M等人[11]利用快速傅里叶变换、原始信号统计特征等方法,也达到了滚动轴承故障诊断的目的。

在实际工程应用中,轴承振动信号受强背景噪声及其他设备激励源的影响,早期微弱故障特征不易提取,上述方法实际应用受限。针对强背景噪声这一问题,SAWALHI N等人[12]提出了一种最小熵反卷积(minimum entropy deconvolution, MED)的滚动轴承故障检测方法;但是研究者使用MED方法对信号降噪时,并未考虑轴承冲击特征。MENG Zong等人[13]提出了一种自回归移动平均和多点最优MED的轴承故障诊断方法,该方法能够从强背景噪声中分离周期性脉冲故障特征。

近年来,MCKD[14]被广泛应用于信号的降噪及滤波处理。WANG Zhi-jian等人[15]提出了MCKD与VMD相结合的轴承早期微弱故障特征提取方法。李政等人[16]提出了MCKD与改进经验小波变换相结合的轴承早期故障诊断方法,利用MCKD对原始信号进行了降噪处理,提取了周期性脉冲信号;但MCKD降噪效果受关键参数滤波长度L、反卷积周期T及滤波器位移数M的影响,且很大程度上依赖专家先验知识。DENG Wu等人[17]利用人工鱼群算法对MCKD关键参数进行了优化,实现了最佳反卷积和故障特征分离的目的。刘奇等人[18]利用最大重叠离散小波包变换对轴承原始信号进行了分解,选取峭度较大的分量进行了MCKD滤波,实现了信号降噪目的。

但是以上算法只针对滤波长度L、解卷积周期T进行了寻优,并未考虑M的影响,而且算法参数多、计算量大,算法的实用性并不强。

针对风力发电机轴承早期微弱故障不易提取的问题,笔者提出一种基于MOBWO-MCKD的风力发电机滚动轴承故障特征提取方法。

首先,笔者利用MOBWO[19]优化MCKD的滤波长度L、解卷积周期T、滤波器位移数M,以生成最佳解卷积信号,有效消除噪声及其他设备激励源的影响,突出冲击特征;其次,对解卷积信号进行包络解调,以提取轴承故障特征频率;最后,采用实际采集的风力发电机轴承数据,对MOBWO-MCKD方法进行有效性验证。

1 理论介绍

1.1 最大相关峰度反卷积

最大相关峰度反卷积(MCKD)本质为利用反卷积运算提高原始信号的峰度值,突出淹没在强背景噪声中的连续脉冲信号。

峰度表达式为:

(1)

式中:y为传感器测量的输出信号;M为位移数;T为反卷积周期。

Ts=fs*T

(2)

式中:fs为采样频率;Ts为冲击周期。

对于输入的原始振动信号x,输出信号y,求最优滤波器f:

(3)

为了求最优滤波器f,需满足:

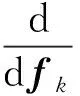
(4)

由式(1)～式(4)可知,滤波器f最终表达式为:

(5)

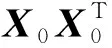
其中:

1.2 多目标白鲸优化算法

多目标白鲸优化算法(MOBWO)模拟了鲸鱼的游泳和觅食行为,其主要包含探索阶段和开发阶段。根据种群机制改变自身位置向量在空间进行搜索,其中每条白鲸代表一个候选方案,在迭代过程中进行寻优。

物理表达式为:

(6)

式中:N为白鲸的种群数量;d为变量维数。

适应度表达式为:

(7)

猎物初始位置未知,白鲸初始位置随机布置。当白鲸探索到最优猎物位置时,所有白鲸包围猎物,采用平衡因子Bf从探索阶段过渡到开发阶段,其表达式为:

(8)

式中:T为当前迭代次数;Tmax为最大迭代次数,B0在[0,1]随机变化。

平衡因子Bf>0.5时为探索阶段,白鲸种群根据最优个体探索猎物;Bf≤0.5时,种群利用随机个体探索猎物。

整个过程中,白鲸位置表达式为:

(9)

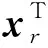
式(9)中的A和L可表达为:

(10)

(11)

(12)

式中:u和v为正态分布随机数;β为常数,此处取β=1.5。

1.3 MOBWO改进MCKD方法

笔者采用MOBWO强大的全局和局部寻优能力,将MCKD的包络谱熵作为MOBWO的适应度函数,其值的大小代表原始信号的冲击周期。原始信号背景噪声值越大,有效特征越微弱,则包络熵越大,表达式如下:

(13)

式中:N为采样点数;pj为包络谱概率分布密度。

笔者定义滤波长度L、反卷积周期T及滤波器位移数M为MOBWO的寻优空间,则有:

Xi=[Li,Ti,Mi]

(14)

多目标自适应优化L、M、T的过程如下:

1)初始化种群;

2)设定白鲸数量10,Tmax=50,探索者数量7,开发者数量3;

3)设定L∈[20,400],T∈[Ts/fs-40,Ts/fs+40],M∈[1,7];

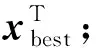
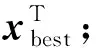
6)若满足最大迭代次数,输出最优结果,对原始信号进行降噪处理,若不满足,则转至步骤4)。

2 基于MOBWO-MCKD的诊断流程

针对风力发电机轴承振动信号受强背景噪声及其他设备激励源影响,导致早期微弱故障特征不易提取这一问题,笔者提出了基于MOBWO-MCKD的风力发电机轴承故障诊断方法。

首先,该方法采用MOBWO强大的全局及局部搜索能力优化MCKD关键参数;然后,使用MCKD对原始信号进行卷积运算,消除噪声及其他设备激励源的影响,突出轴承的周期性脉冲信号;最后,对解卷积信号进行包络谱分析,达到轴承故障诊断的目的。

基于MOBWO-MCKD的故障诊断流程如图1所示。

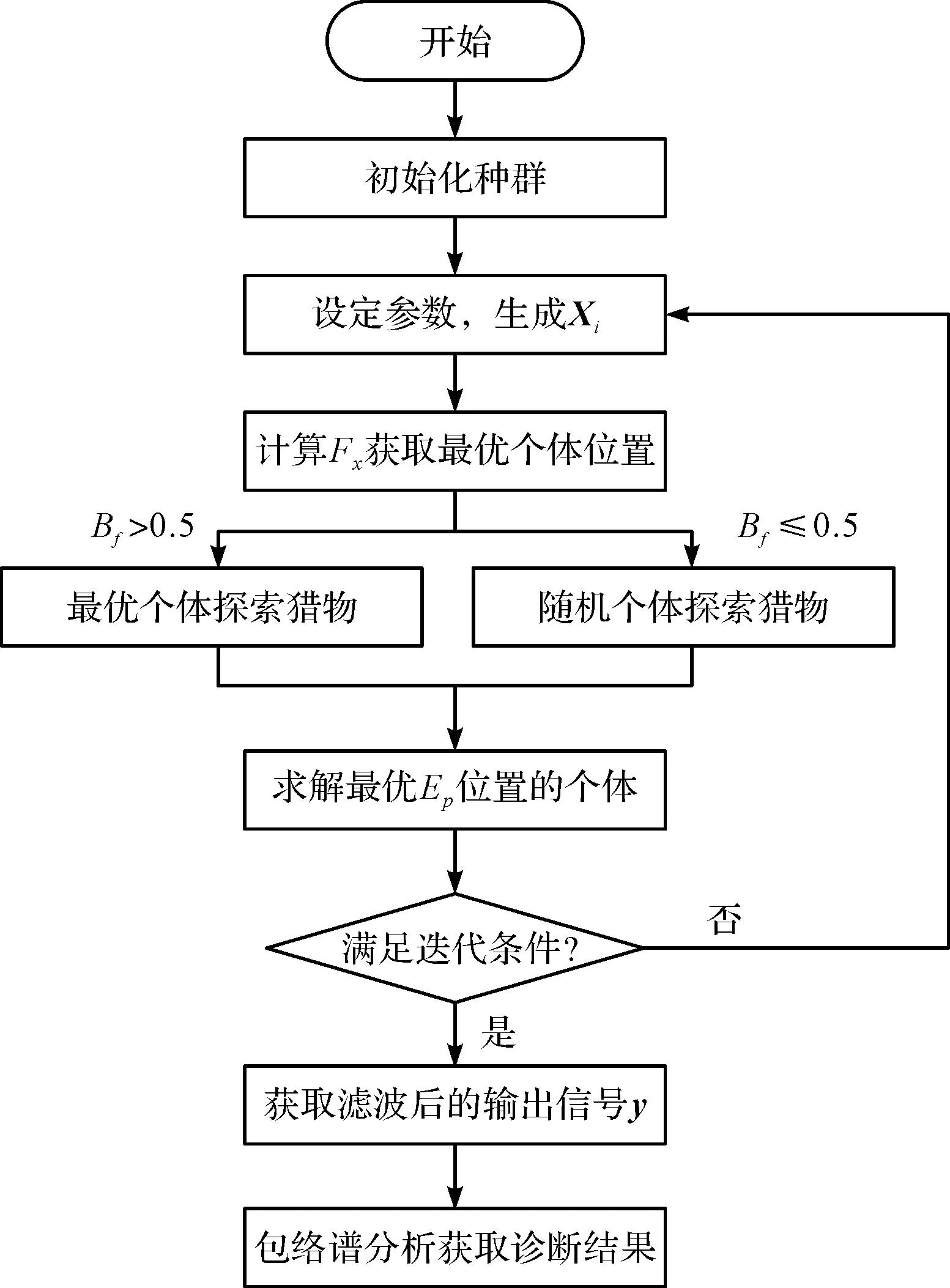
图1 MOBWO-MCKD故障诊断流程图Fig.1 MOBWO-MCKD fault diagnosis flowchart

3 试验及结果分析

为了验证MOBWO-MCKD在强背景噪声干扰下对风力发电机轴承故障特征提取的有效性,笔者采用实际采集到的风力发电机轴承数据对MOBWO-MCKD进行具体的试验验证。

3.1 试验数据来源

试验数据由河北某2 MW风场提供。该风场发电机型号为湘潭电机,轴承型号为SKF6332。其参数如表1所示。

表1 SKF6332参数Table 1 SKF6332 parameters

发电机轴承承受交变载荷,采用脂润滑。采样频率为16 384 Hz,采样时长为10 s,发电机转速为1 570 r/min。

数据采集如图2所示。

图2 风力发电机轴承振动信号采集Fig.2 Wind turbine bearing signalacquisition

轴承故障如图3所示。

图3 轴承故障Fig.3 Bearing fault

图3(a)中,轴承内圈故障形式为电腐蚀故障,故障损伤点均匀分布在内圈表面;图3(b)中,轴承外圈故障形式为不规则形状局部疲劳脱落。

3.2 内圈故障分析

内圈故障信号时域波形、频谱如图4所示。

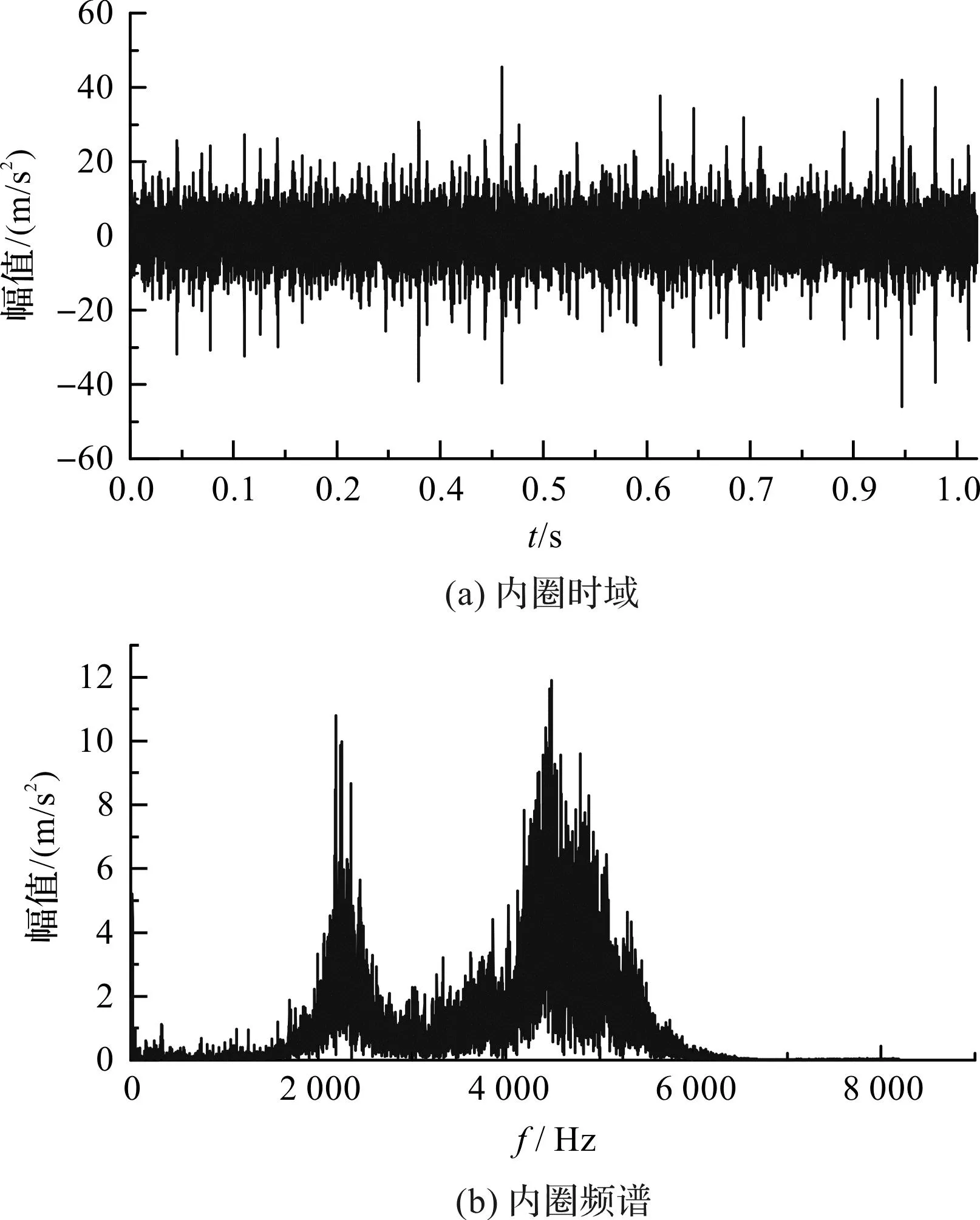
图4 内圈故障时域波形、频谱 Fig.4 Time domain waveform and spectrum of inner ring fault

笔者分别采用MOBWO-MCKD、白鲸优化算法(beluga whale optimization, BWO)优化MCKD(BWO-MCKD)和原始信号直接包络方法进行对比分析。

首先,利用优化后的MCKD对原始信号进行降噪处理(MCKD参数为:M=7,L=160,T=108),MOBWO-MCKD降噪后轴承时域信号结果如图5所示。

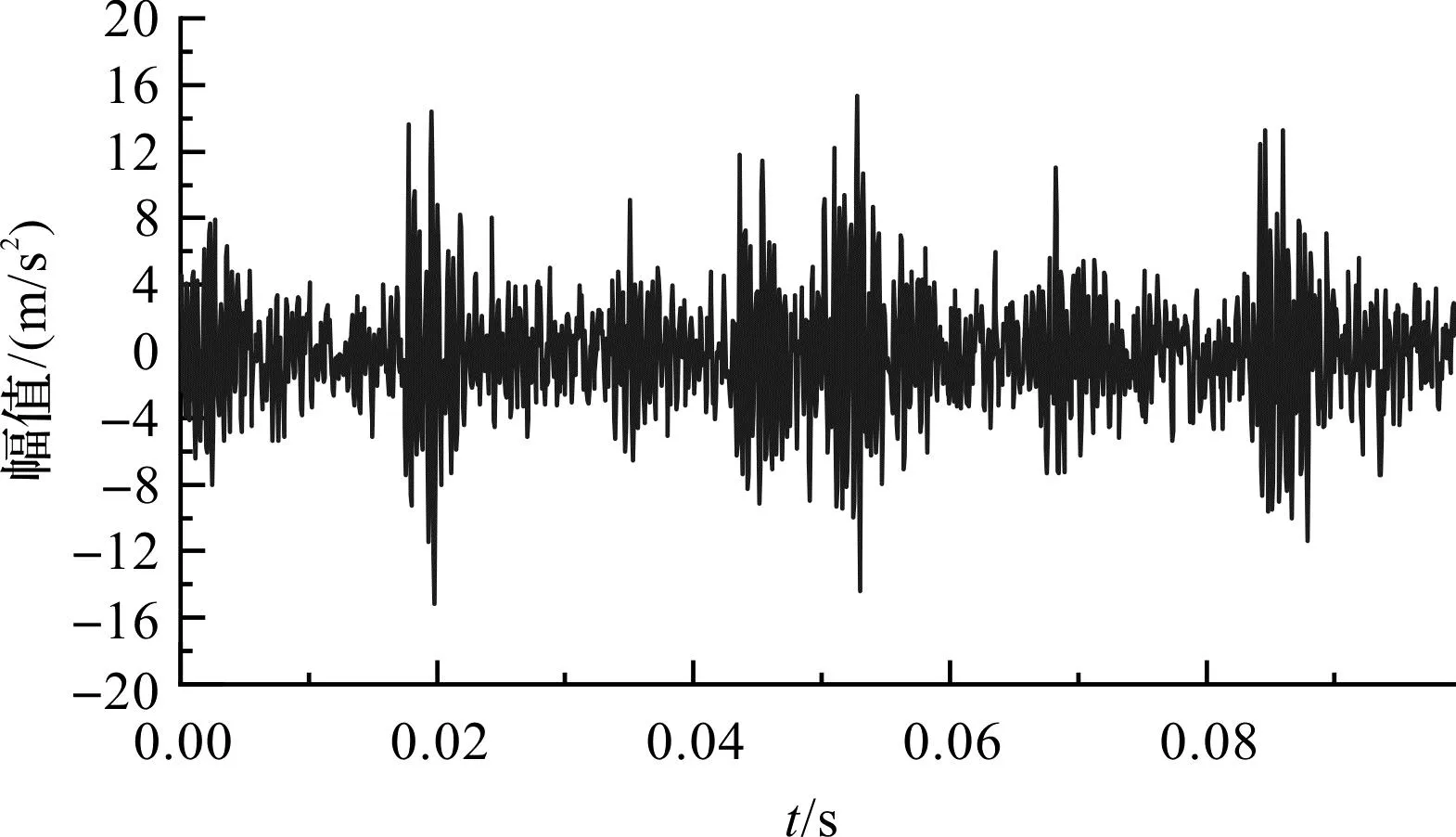
图5 MOBWO-MCKD降噪后轴承时域信号 Fig.5 Bearing time domain signal after MOBWO-MCKD noise reduction

由图4(a)和图5对比可知:背景噪声及其他设备激励源等干扰因素明显消除,突出冲击特征。

笔者对降噪后的时域信号进行了包络谱分析,结果如图6所示。

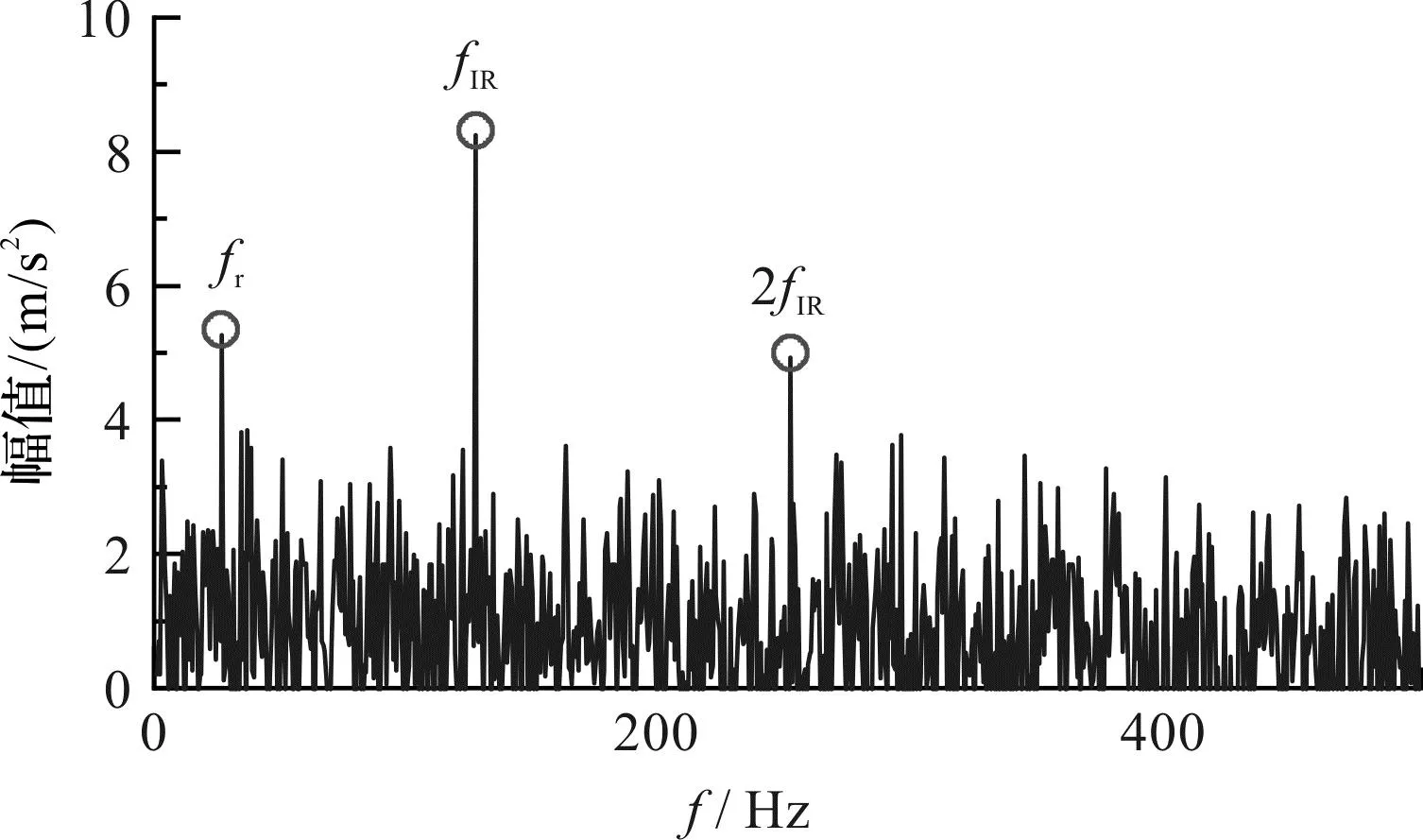
图6 MOBWO-MCKD降噪后包络谱Fig.6 Envelope spectrumafter MOBWO-MCKD

由图6包络谱可看出:轴承内圈故障特征频率fIR=125.87 Hz、2fIR=251.74 Hz,与理论计算轴承内圈故障频率一致,由此可诊断出轴承内圈故障。

笔者对图4(a)所示的轴承时域信号采用BWO-MCKD和直接包络进行对比分析。

BWO-MCKD分析结果如图7所示。

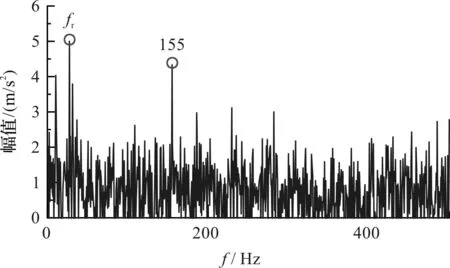
图7 BWO-MCKD降噪后包络谱Fig.7 Envelope spectrum after BWO-MCKD

由图7可看出:使用BWO-MCKD降噪后,包络谱图噪声等干扰因素较多,未找到内圈故障特征频率。

原始信号直接包络分析结果如图8所示。

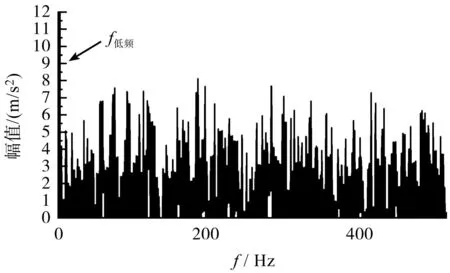
图8 原始信号包络谱Fig.8 Original signal envelope spectrum

由图8可看出:原始信号包络谱图存在低频干扰,未发现内圈故障特征频率。

3.3 外圈故障分析

外圈故障信号时域波形、频谱如图9所示。

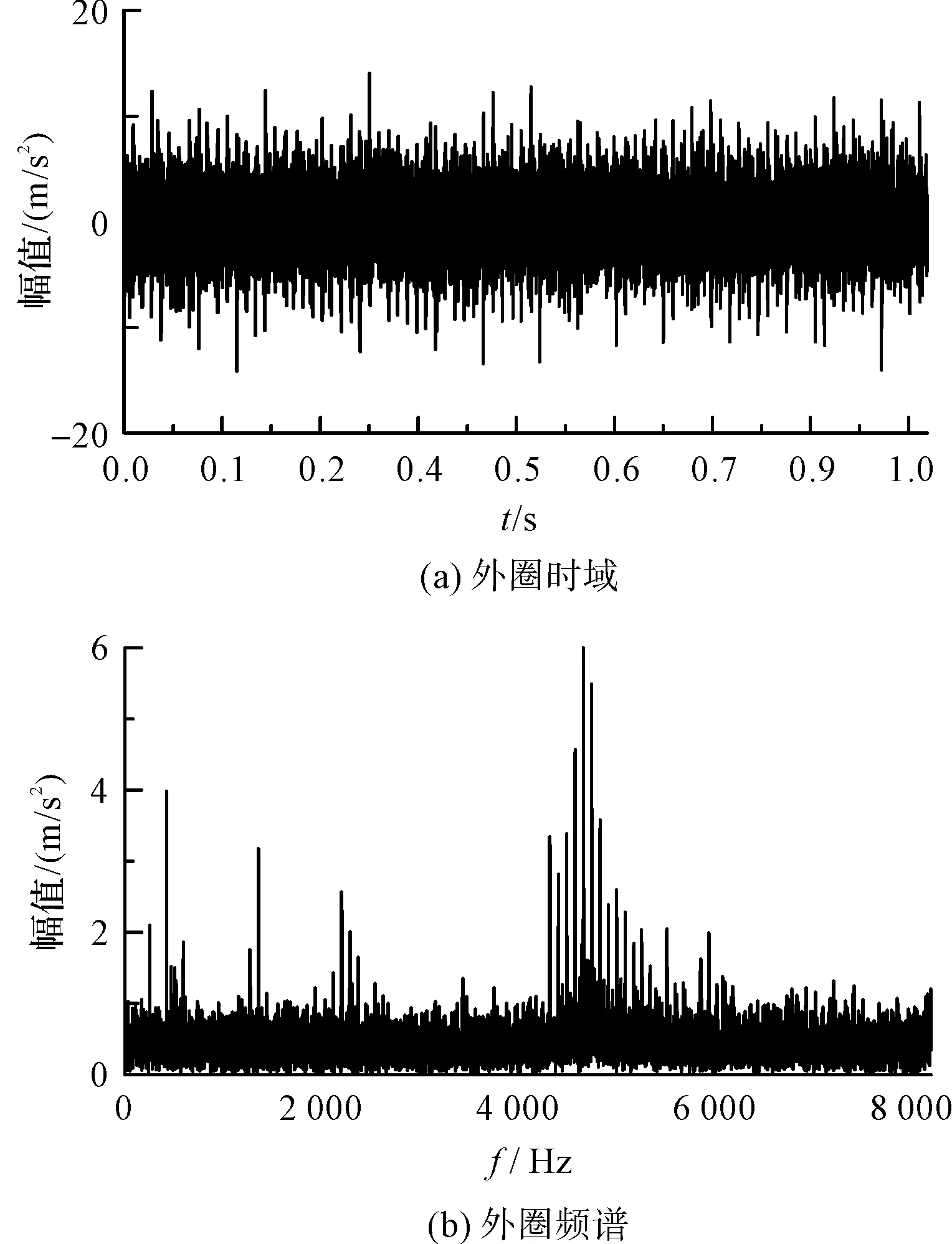
图9 外圈故障时域波形、频谱Fig.9 Time domain waveform and spectrum of outer ring fault

笔者分别对MOBWO-MCKD、BWO-MCKD和原始信号直接包络进行对比分析。

首先,采用优化后的MCKD对原始信号进行降噪处理,MCKD参数为:M=5,L=140,T=163,结果如图10所示。

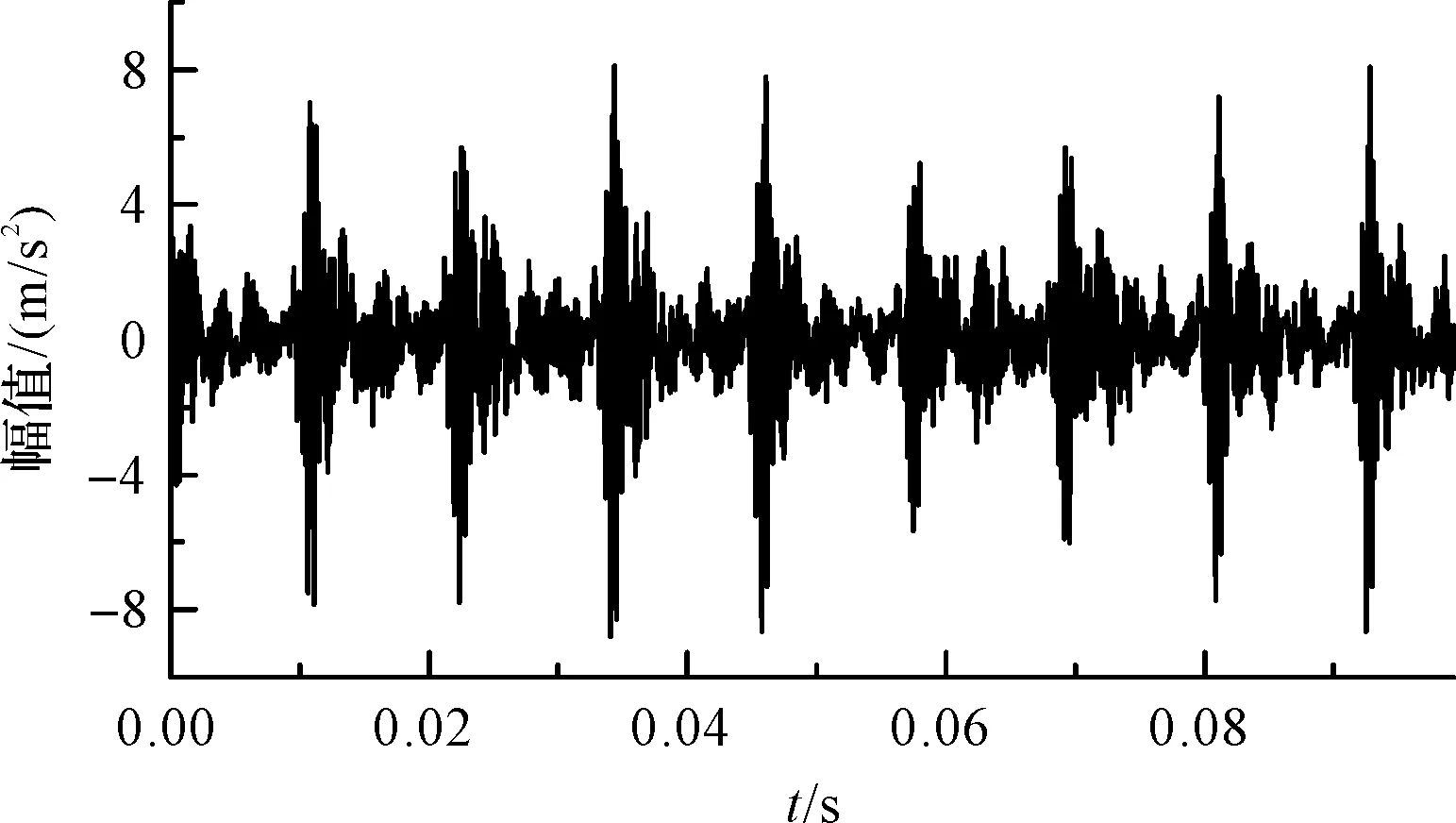
图10 MOBWO-MCKD降噪后轴承时域信号 Fig.10 Bearing time domain signal after MOBWO-MCKD noise reduction

由图9(a)和图10对比可知:背景噪声及其他设备激励源等干扰因素明显消除,突出冲击特征。

笔者对降噪后的时域信号进行包络谱分析,结果如图11所示。

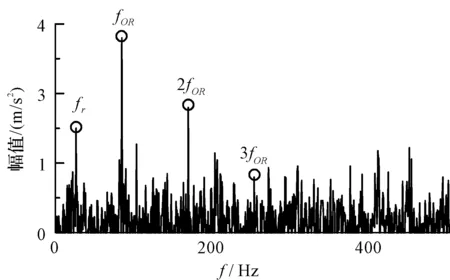
图11 MOBWO-MCKD降噪后包络谱Fig.11 Envelope spectrum after MOBWO-MCKD

由图11包络谱可知:轴承外圈故障特征频率fOR=84.47 Hz、2fOR=168.94 Hz、3fOR=253.41 Hz,其与理论计算轴承外圈故障频率一致,由此可以诊断出轴承外圈故障。

笔者对轴承外圈时域信号采用BWO-MCKD和直接包络进行对比分析。

BWO-MCKD分析结果如图12所示。

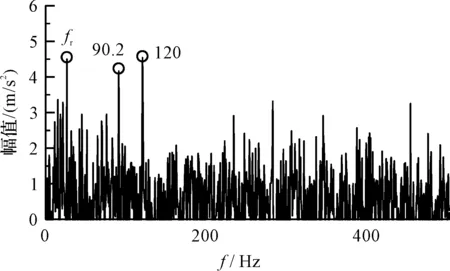
图12 BWO-MCKD降噪后包络谱Fig.12 Envelope spectrum after BWO-MCKD

图12中,噪声等干扰因素较多,未找到外圈故障特征频率。

原始信号直接包络分析结果如图13所示。

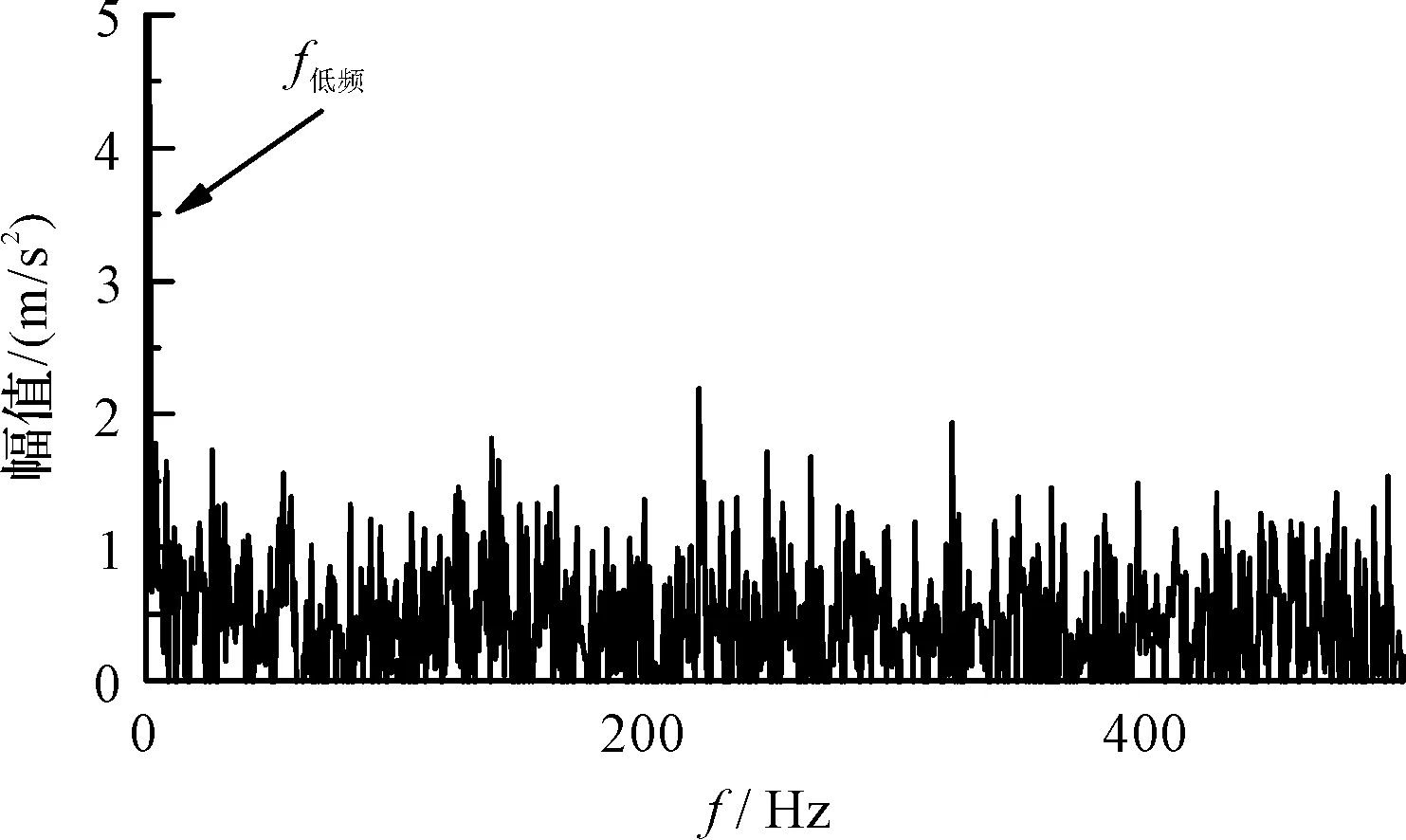
图13 原始信号包络谱Fig.13 Original signal envelope spectrum

图13中,存在低频干扰,未发现外圈故障特征频率。

综上所述,笔者提出的基于MOBWO-MCKD的方法可有效消除强背景噪声及其他设备的激励源影响,突出冲击特征。笔者对降噪后的时域信号进行包络谱分析,可有效提取出轴承故障特征频率,实现强背景噪声及其他设备激励源干扰下的轴承故障诊断的目的。

4 结束语

针对风力发电机轴承振动信号受强背景噪声及其他设备激励源影响导致早期微弱故障特征不易提取这一问题,笔者提出了一种MOBWO优化MCKD的风力发电机轴承故障特征提取方法,即基于MOBWO-MCKD的方法。

研究结果表明:

1)采用经过MOBWO优化后的MCKD对原始信号进行了卷积运算,可有效消除噪声及其他设备激励源的影响,突出轴承的周期性脉冲信号;

2)对解卷积信号进行了包络谱分析,有效提取了fIR=125.87 Hz、2fIR=251.74 Hz的轴承内圈故障特征频率,以及fOR=84.47 Hz、2fOR=168.94 Hz、3fOR=253.41 Hz的轴承外圈故障特征频率,验证了MOBWO优化后的MCKD的有效性;

3)与传统的故障诊断方法进行了对比分析,证明笔者所提基于MOBWO-MCKD的风力发电机滚动轴承故障特征提取方法诊断效果最好,验证了其优越性,对实际工程风力发电机轴承故障诊断研究具有一定的应用价值。

在后续的研究中,笔者将进一步对现有方法进行优化,使其适用于风力发电机轴承内外圈复合故障诊断以及行星齿轮箱故障诊断。