基于仿真数据和子领域自适应的轴承故障网络诊断框架*

韩 洁,苏小平,康正阳

(南京工业大学 机械与动力工程学院,江苏 南京 211800)

0 引 言

轴承被誉为“工业的关节”,被广泛应用于国民经济和国防建设各个领域。因此,对轴承的运行状态进行监测和故障诊断具有重要的意义[1]。

随着人工智能的快速发展,深度学习在轴承故障诊断领域得到了广泛研究,通过模型训练可以端到端地自动识别轴承的故障类型和故障程度[2]。然而,深度学习模型的优异诊断性能离不开大量同分布的数据样本[3]。

在实际工业场景中,由于机械大部分时间处于正常工作状态,通常难以事先获取同一设备、同一工况下充足的故障数据用于深度学习模型训练,这限制了人工智能在工业场景下的应用。

通过数字孪生进行虚拟实验,能够以较低的成本和较高的灵活度获取大量数据,为解决深度学习缺乏训练样本的问题提供了可能[4]。

SOBIE C等人[5]利用轴承三自由度动力学模型获取了故障数据,并在卷积神经网络的基础上,实现轴承故障识别的目标。LIU Xiao-yang等人[6-7]分别建立了轴承故障和齿轮故障有限元模型,将其应用于故障诊断方法研究中,取得一定的成果。LUO Wei-chao等人[8]提出了一种基于模型和数据的数字孪生混合模型,完成了数控机床的预测性维护工作。

然而,仿真模型是理想化的工程设计,通过模拟得到的数据往往与实际测量得到的数据存在较大差异,导致神经网络的泛化能力降低。

针对训练样本与测试样本差异大的问题,迁移学习能够将源域的知识迁移到相关目标域的任务上,以提升模型在目标域上的分类精度。

XU Yan等人[9]利用数字化车间的数字孪生模型生成了大量仿真数据,并对其进行了训练,采用少量的真实标签样本对模型进行了微调,完成了对真实样本的故障分类任务;但在实际场景下,要获取少量真实故障样本仍存在困难。LIU Chen-yu等人[10]通过建立轴承数字孪生模型,获取了轴承退化数据,并使用对抗迁移方法,将仿真数据用于实际实验台中的剩余寿命预测问题研究;但其对抗迁移方法存在着收敛困难的问题,导致模型难以进行训练。董绍江等人[11]采用条件最大均值差异法,缩小了仿真数据与实际数据的差异,进而提高了无标签样本场景下的轴承故障分类精度;但该方法只对源域和目标域特征进行了全局对齐,因此容易导致负迁移现象的出现。

为了解决以上问题,笔者采用数学建模和有限元仿真两种方式生成轴承故障仿真数据,研究不同轴承故障模型生成的仿真信号对实际信号的迁移能力;同时,为了提高基于模拟故障信号训练的模型在真实故障数据上的分类精度,利用深度子领域自适应方法对齐源域和目标域的全局分布和相关子领域的分布;最后,在ResNet模型架构上进行端到端的轴承故障诊断。

1 轴承故障数学建模

1.1 轴承故障模型

轴承故障时产生的冲击振动可以看作脉冲序列函数,笔者将故障信号建模为伪循环平稳过程,考虑转频调制和滚动体滑移现象,对轴承内圈故障和外圈故障模型进行简化。

其表达式如下[12]:

(1)

h(t)=exp(-Bt)sin(2πfnt)

(2)

Ak=A0sin(2πfrt)+1

(3)

式中:ffault为滚动体经过内圈或外圈故障点时产生冲击信号的频率;h(t)为单次欠阻尼衰减振动信号;B为衰减系数;fn为共振频率;Ak为冲击信号的幅值,当轴承载荷方向不变,轴承外圈固定,内圈随轴旋转时,外圈故障冲击信号的幅值没有调制现象,内圈故障冲击信号的振幅受到转频fr调制,用频率为fr的正弦(或余弦)函数表示;fr为转频;n(t)为高斯白噪声;tk为第k次冲击相对于故障周期的微小波动,采用均值为0、标准差为0.005fr的正态分布表示。

未加噪的轴承内圈故障模拟信号如图1所示。

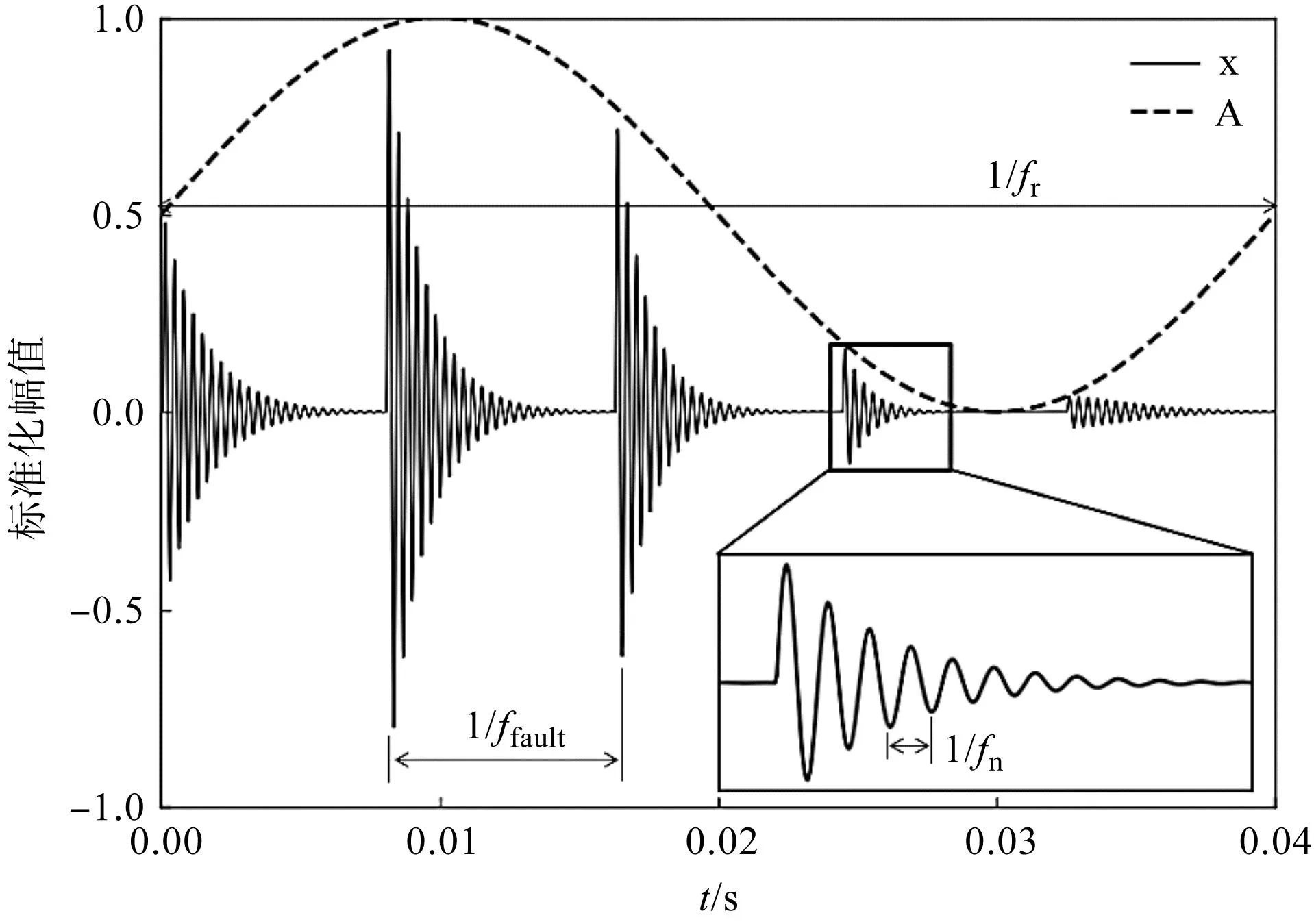
图1 内圈故障模拟信号Fig.1 Simulation signal of inner race fault

滚动体经过内圈或外圈故障点时,产生冲击信号的频率称为故障频率,其计算公式[13]如下:

(4)

(5)

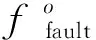
此处的仿真模型选用6203型轴承,轴承转速为1 500 r/min。

相应轴承故障模型参数设置如表1所示。

表1 轴承故障模型参数Table 1 Parameters of bearing fault model

1.2 模型可靠性验证

针对数学建模得到的仿真信号,笔者又添加了信噪比为0的噪声。

外圈故障和内圈故障信号及其包络谱如图2所示。

图2 故障模拟信号及其包络谱Fig.2 Simulated signals and envelope spectrograms

图2中包络谱上的等间隔虚线表示故障频率及其倍频。

从图2中可见:从外圈故障信号包络谱中提取到了外圈故障频率及其倍频,内圈故障信号包络谱中展现了调制现象,在内圈故障频率周围有大小为1倍转频的边频带。

这表明,轴承故障数值模型是有效的。

2 轴承故障有限元仿真

2.1 模型建立

笔者以6203型深沟球轴承为建模对象进行显式动力学分析。

轴承尺寸参数为:滚动体直径6.75 mm,节圆直径14.525 mm,外径40 mm,孔径17 mm,滚动体数量8个。

为了与实际工作轴承更加接近,笔者在其建模过程中,设置径向间隙为0.02 mm,兜孔间隙为0.35 mm;采用SKF方形法兰盘式轴承座,并进行简化;在HyperMesh中采用渐变网格划分,对轴承外圈内表面和内圈外表面部分进行网格细化,单元大小为0.3 mm～1 mm。

笔者采用LS-DYNA前处理软件LS-PrePost进行显式动力学分析设置。

轴承内圈、外圈和滚动体材料为轴承钢,保持架材料为黄铜。笔者对轴承内圈内表面节点建立节点刚体,并施加径向载荷和转速,参数值根据实际工况而定。滚动体与内圈、外圈和保持架之间采用自动面面接触;轴承外圈外表面节点与轴承座内表面设置绑定接触;轴承座螺栓孔位置设置固定约束;仿真过程中考虑重力因素;在LS-PrePost中通过删除单元方式以简单模拟局部故障。

建立的轴承故障有限元模型如图3所示。

图3 轴承故障有限元模型Fig.3 Finite element model of the fault bearing

2.2 模型可靠性验证

通过显式动力学仿真得到了节点加速度信号及其包络谱,如图4所示。

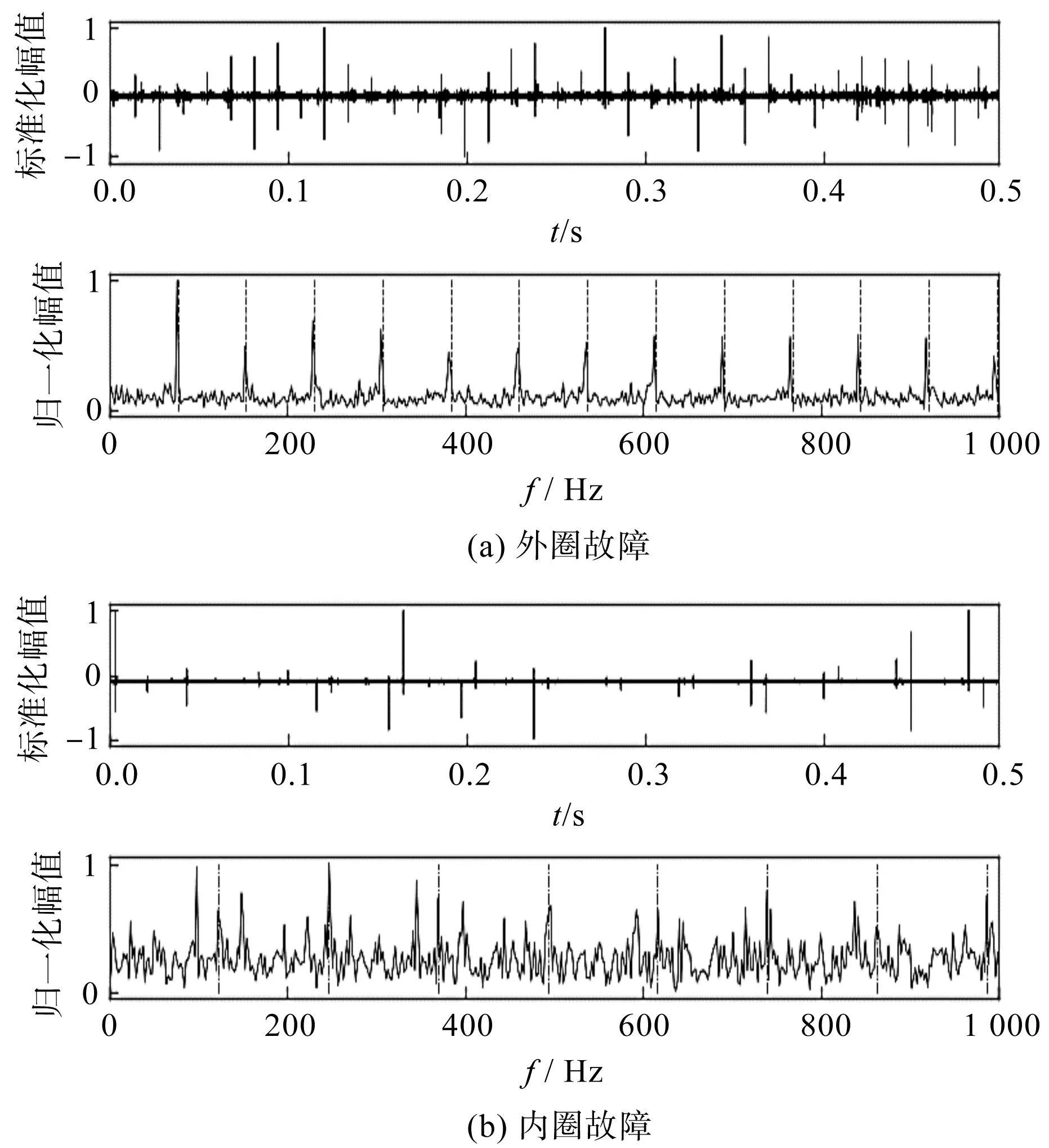
图4 故障模拟信号及其包络谱Fig.4 Simulated signals and envelope spectrograms

从图4中可观察到:经过动力学仿真得到的冲击信号包含很多数值噪声,且冲击信号幅值有较大波动;但其希尔伯特包络谱中仍提取到了故障频率及其倍频,在一定程度上表明了基于显式动力学建立的轴承故障模型的有效性。

3 子领域自适应轴承故障诊断网络

3.1 子领域自适应

现实场景中,往往缺少可供训练的大量标签数据,通过迁移学习可以将在大数据上训练的大模型应用到下游相关小数据任务上。

在迁移学习中,一般将具有大量数据的任务称为源域,将具有少量标签数据或无标签数据的任务称为目标域。当目标域含标签信息时,可以利用微调的方式将在源域数据上训练的模型应用到目标域上;当目标域不含标签信息时,由于源域数据和目标域数据存在差异,迁移学习性能往往受到限制。

因此,领域自适应方法被提出以减少源域和目标域之间的分布差异,实现无标签数据下的分类识别目的[14]。

深度子领域自适应(deep subdomain adaptation network, DSAN)[15-16]是无监督领域自适应方法中的一种。它利用偏差度量的方法,缩小源域特征和目标域特征的差异。与大多数全局分布对齐方法不同,DSAN中提出的局部最大均值差异(local maximum mean discrepancy, LMMD)可以拉近相关子域的分布,实现同一类别特征的对齐。

最大均值差异[17](max mean discrepancy,MMD)测量的是再生希尔伯特空间中两个特征分布的距离。与经典MMD相比,LMMD利用了源域真实标签和目标域伪标签,在计算最大均值差异过程中给核函数添加了以类别信息表示的权重,这可以拉近同一类别相关子域的特征分布。

其计算公式如下:

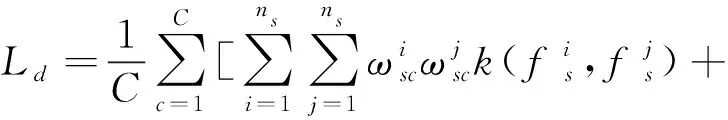
(6)

(7)

式中:k(,)为核函数;fs为源域特征;ft为目标域特征;C为类别数;ns为源域特征个数;nt为目标域特征个数;y为源域真实标签或目标域预测标签。

3.2 模型框架

笔者提出的轴承故障诊断模型架构如图5所示。

图5 故障诊断模型框架Fig.5 Diagram of the diagnostic model structure

模型采用原始一维振动信号作为输入,信号输入维度为4 096,特征输出维度为128,标签输出维度为3。

模型中包含两个目标损失,领域自适应损失用来拉近源域特征和目标域特征的距离,分类损失用来度量源域数据的预测标签和真实标签的差异,其计算公式如下:

(8)

式中:Ds为源域样本分布;C为类别数;yr为源域真实标签;ys为源域预测标签。

模型训练过程中优化的目标损失函数如下:

L=Ly+Ld

(9)

基础模型参考残差网络(ResNet)[18],并根据输入信号特征对模型参数进行改进。

该模型由卷积核堆叠而成,每个卷积核后都跟随批量归一化层和ReLU激活函数。基础模型一共包含五个模块,其中针对输入信号尺寸过大的特点,在第一个模块中使用尺寸为32、步长为8的大卷积核;其余四个模块各包含两个尺寸为3的卷积核和残差结构,在每个模块后添加平均池化层以降低输入尺寸。

模型具体参数如表2所示。

表2 ResNet模型参数Table 2 Parameters of ResNet

4 实验验证

4.1 数据集和模型参数介绍

笔者采用德国帕德博恩大学轴承故障数据集[19]7对上述方法的有效性进行验证。

模块化实验平台如图6所示。

图6 模块化实验平台Fig.6 Modular test rig

实验轴承型号为6203,轴承内圈故障和外圈故障采用电火花加工,轴承转速为1 500 r/min,径向载荷为1 000 N,采样率为64 kHz。

三种轴承故障实验信号[19]10如图7所示。

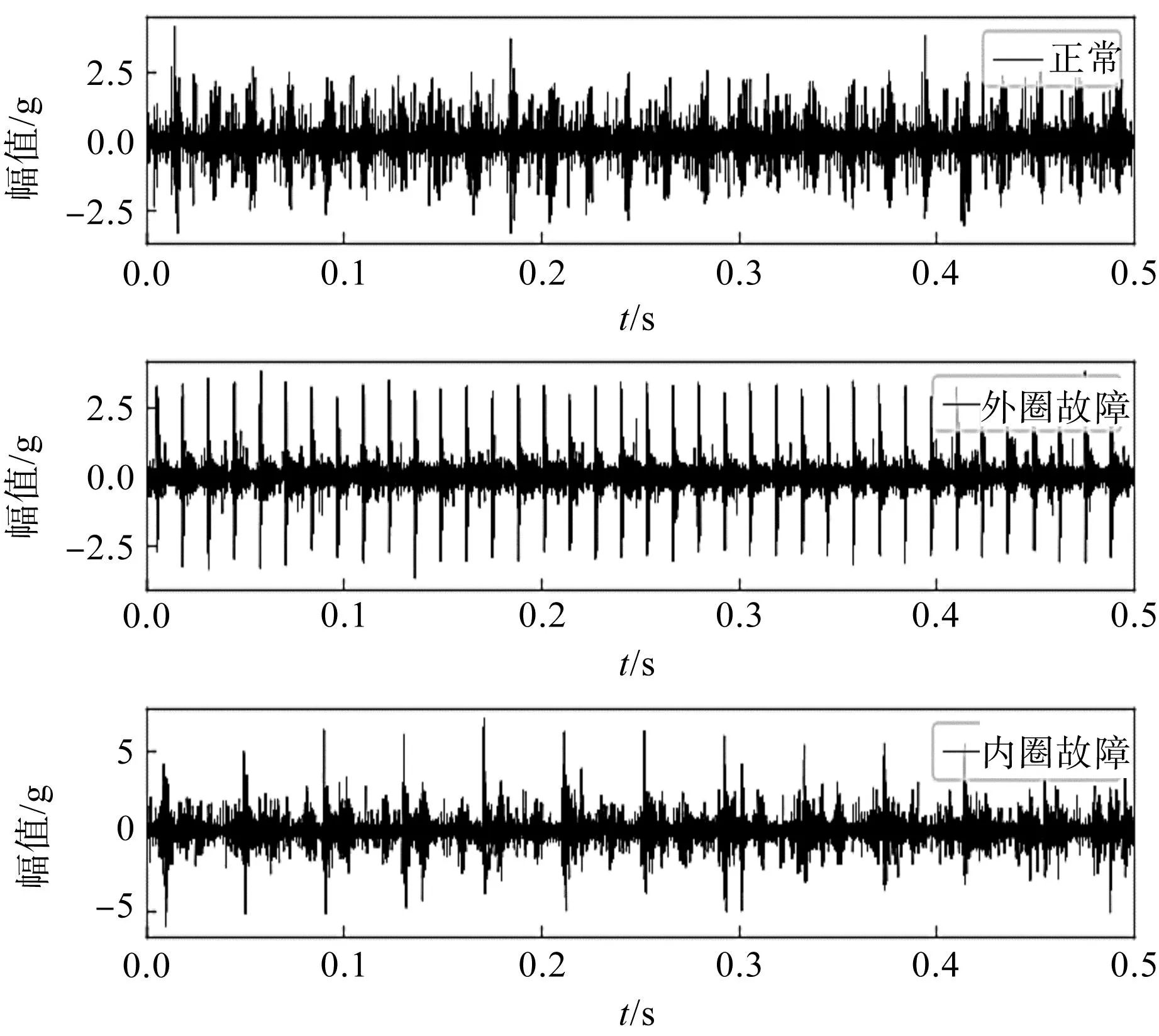
图7 轴承故障实验信号Fig.7 Experimental signals

笔者分别利用数学建模和有限元仿真方式生成两种训练数据。显式动力学分析设置仿真时长为0.5 s,单次采集四个节点的垂向加速度,每种故障类型共获得2 s的数据。

为了公平对比,数值模型单次生成长度0.5 s的信号,并对此信号分别添加四种程度的噪声,使其信噪比分别为-2 dB、0 dB、2 dB和4 dB。

为了保证截取后的样本不会丢失故障信息,笔者设置样本长度为4 096个点,不采用重叠采样时一共可以获得约90个样本。

模型总参数量为58 275,初始学习率设置为0.01,学习率采用系数为0.96的指数型衰减策略,训练批次设置为50,权重衰减系数设置为0.000 1,批量大小设置为64。

4.2 实验结果及对比分析

4.2.1 样本大小对模型泛化能力的影响

通过重叠取样,笔者以不同移动步长截取数据,研究不同训练数据量大小对模型泛化能力的影响,此时不计算领域自适应损失。源域训练数据采用数学建模生成的信号,每次实验重复十次。

笔者将十次训练过程中模型分类准确率的均值和最值绘制成图,如图8所示。

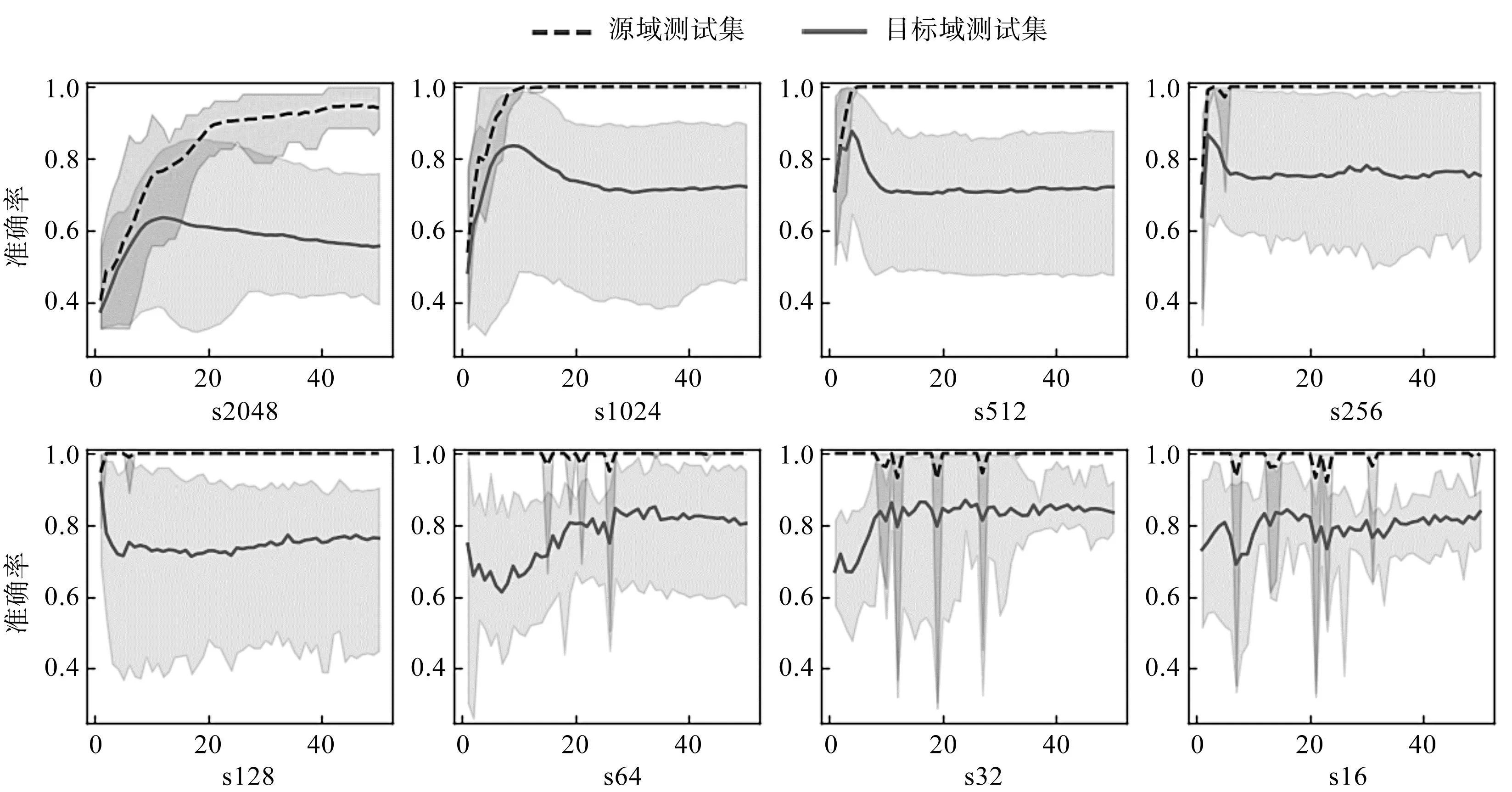
图8 重叠取样不同移动步长下模型精度收敛曲线Fig.8 Model accuracy under different moving steps with overlapping sampling

从图8中可以观察到:

1)当源域训练样本较少时,模型对目标域样本的平均分类准确率先上升后下降,然后趋于平稳。在模型能够对源域测试样本达到100%分类准确率附近时,模型对目标域测试样本的分类准确率达到最高值,此后继续训练模型,使之对源域样本过拟合,导致其对目标域的分类精度下降;

2)当源域训练样本较少时,模型对目标域样本的识别精度波动范围较大,且随着训练批次的增加,波动并没有减小的趋势。由于模型参数量大,根据少量训练样本训练出的模型有无数种拟合源域样本的参数组合。虽然存在某次训练能使模型对目标域达到较高的分类精度,但同时也存在更差的分类结果;

3)当源域训练样本增多时,模型在第一个训练批次,即第一次遍历源域训练样本后,已经可以对源域测试集进行完美分类,此时对目标域的分类精度也较高,此后继续训练,模型对目标域的平均分类精度大致呈上升趋势,且波动逐渐减小。这表明源域样本的增加有利于目标域分类精度的提升和稳定。

最后一个训练批次的模型分类精度如表3所示。

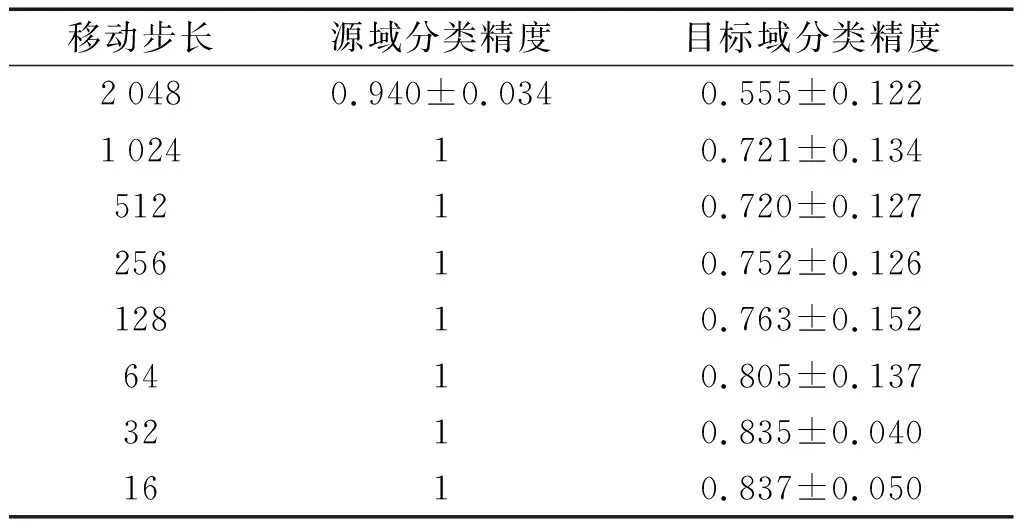
表3 不同数据量下模型的诊断精度Table 3 Diagnostic accuracy under different amounts of data

从表3中可以得知:当移动步长为1 024,源域训练样本约为250个时,模型已经可以对源域样本完成100%的分类精度工作,此时增大数据量对源域分类精度没有影响;但却可以提高模型对目标域样本的分类精度,使模型对目标域的分类精度从72.1%增加到了83.7%,共提升了11.6%。

总之,模型在目标域数据上的平均分类精度随着数据量的增大而增大,最后趋于平缓。这表明重叠采样对于轴承故障信号而言是一种显著有效的数据增强方式,增加源域训练样本的数量能够提高模型对目标域样本的识别精度。

4.2.2 不同领域自适应方法对模型泛化能力的影响

笔者采用重叠取样移动步长为16,约为16 000个训练样本进行无监督领域自适应模型训练。

不同领域自适应方法下,模型对目标域的平均识别精度和标准差如表4所示。

表4 不同领域自适应方法下模型的诊断精度Table 4 Diagnostic accuracy under different domain adaptation methods

表4中,ResNet代表在训练过程中不包含域自适应损失的方法,MMD和LMMD分别代表2种不同领域自适应损失计算方法。

从表中可以得知:不采用领域自适应方法时,模型在目标域上的分类精度较低,波动较大;采用领域自适应方法之后,模型在目标域上的分类精度得到了提升,同时降低了标准差。

子领域自适应损失函数LMMD使模型在目标域上达到了最高分类精度,十次训练的均值为99.73%,相比于经典最大均值差异法的97.6%提高了2.1%,体现了子领域自适应方法的有效性。

4.2.3 不同数据生成方式对模型泛化能力的影响

根据4.2.1节和4.2.2节的实验结果,重叠采样的移动步长选取16,领域自适应损失函数采用LMMD。

笔者对基于数学建模和有限元仿真得到的仿真信号迁移性能进行对比,并保持训练数据量大小一致。

某次实验的混淆矩阵如图9所示。

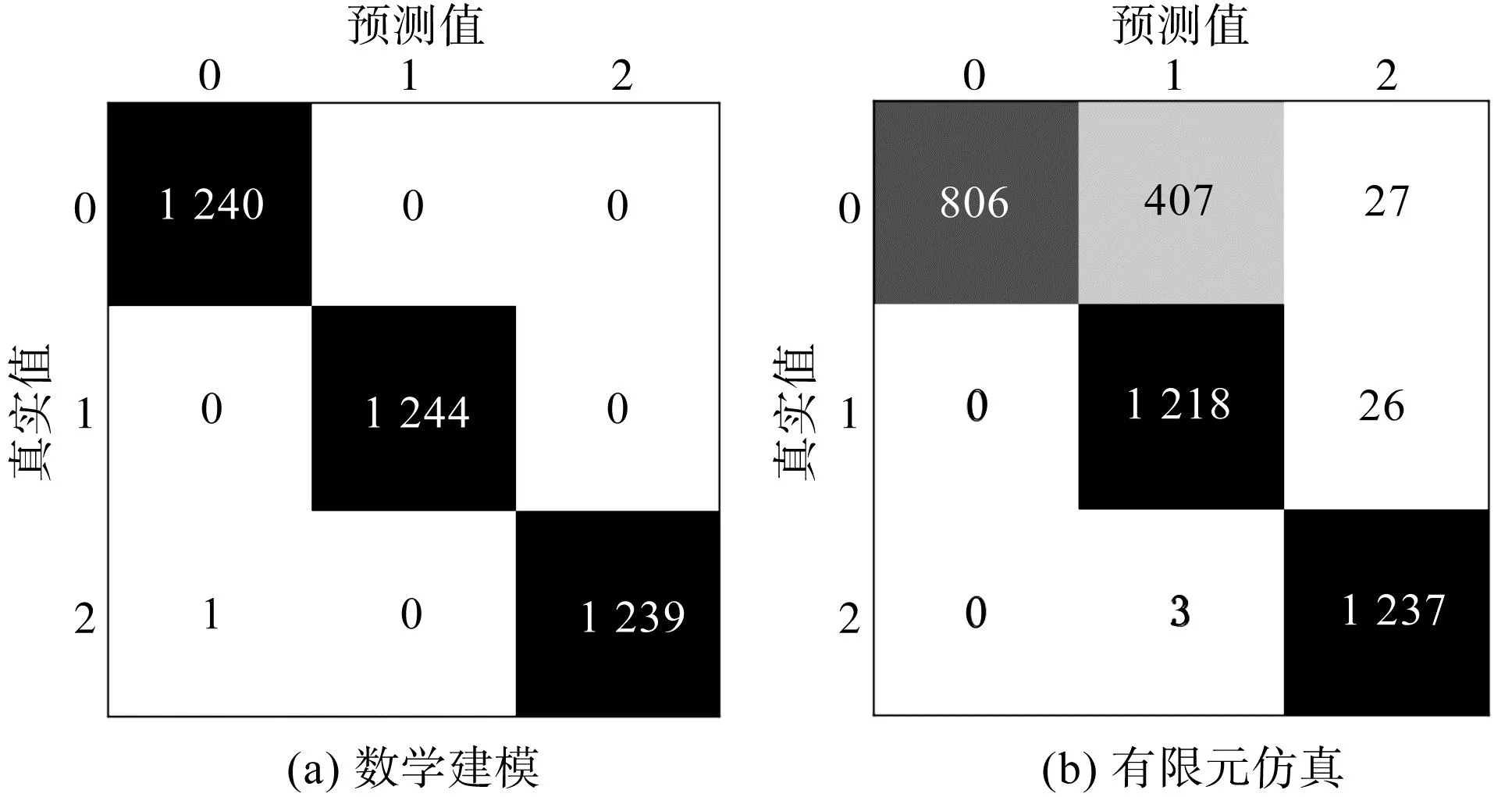
图9 混淆矩阵图Fig.9 Confusion matrix

坐标轴标签0为正常;1为外圈故障;2为内圈故障。

由图9(a)可知:采用数学建模生成的信号作为源域数据进行训练时,目标域真实信号中只有一个内圈故障信号被误分类为正常信号;

而由图9(b)可知:采用有限元仿真生成的信号作为源域数据进行训练时,模型学到的分类知识难以拟合目标域真实故障信号,分类效果较差。

两种仿真信号对实际信号的十次迁移结果如表5所示。

表5 不同数据生成方式下模型的迁移精度Table 5 Diagnostic accuracy under different data generation methods

由表5可见:受建模精度的影响,基于有限元仿真得到的信号对目标域数据的迁移精度较低,只有88.4%;基于数学建模生成的信号与实际信号较为接近,采用子领域自适应方法后对实际信号的迁移精度达到了99.7%,相比于有限元仿真提高了11.3%,体现了数学建模方法生成轴承故障信号在无监督轴承故障诊断领域的有效性。

5 结束语

在实际工业环境中,往往缺乏相应工况的轴承故障数据用于模型训练,这限制了深度学习在工业场景中的应用。

基于此,笔者采用两种建模方式生成了轴承故障信号,将其用于训练模型,并利用深度子领域自适应方法,缩小了模拟信号和真实信号间的差异,提升了模型对真实信号的诊断精度。

研究结果表明:

1)在对源域测试样本分类精度保持不变的情况下,通过对源域训练样本重叠采样,使模型对目标域的分类精度增加了11.6%,表明重叠采样对振动信号来说是一种简单却极为有效的数据增强方式,增加源域数据可提升模型在目标域的分类精度;

2)在进行无监督领域自适应模型训练时,子领域自适应方法相比于最大均值差异法提高了2.1%,表明子领域自适应方法可有效提升模型在无标签目标域上的分类精度;

3)相比于有限元仿真,数学建模生成的仿真信号对真实信号的迁移精度提高了11.3%。基于有限元仿真的数据生成方法受限于个人建模水平,在较长的仿真过程中容易出现不可控现象,导致对实际故障数据的迁移能力较差。基于数学建模的数据生成方法灵活性大、可控性好,对实际信号的迁移精度高,作为故障信号生成工具,其可降低对模拟试验台的依赖,缩减成本。

在后续的研究中,笔者将对旋转机械的数字孪生模型进行深入研究,以提高模型仿真精度,为实际工业系统与人工智能搭建桥梁。