齿向修鼓和轴向错位直齿轮副刚度的计算方法*

朱文轩,张书维,王 琳,周海川

(1.江苏安全技术职业学院 机械工程学院,江苏 徐州 221011;2.南京航空航天大学 自动化学院,江苏 南京 211106)

0 引 言

分析时变啮合刚度激励的变化规律是反映齿轮副啮合特性的有效途径。许多学者都对时变啮合刚度的计算方法进行了研究。

该类研究所采用的方法一般可分为以下3类:有限元法、解析法、解析—有限元法。

其中,有限元法可以自动模拟实际齿廓,包括齿廓修形、加工误差和安装误差,对时变啮合刚度的分析具有较高的精度。WANG Jian-de等人[1-2]综合运用2D与3D单元,对轮齿进行了自适应网格划分,构建了通用的有限元模型,结合数值分析方法计算了传动误差、载荷分布以及扭转啮合刚度。LI Run-fang等人[3]采用三维接触有限元法,对某型减速箱的动力学特性进行了仿真,确定了齿轮箱的刚度激励和误差激励。LI Shu-ting[4]采用了有限元软件,定量研究了加工误差和装配误差对一对直齿轮的承载能力、载荷分配以及传动误差的影响。WU Yong-jun等人[5]运用有限元分析方法,详细讨论了滑动摩擦和时变啮合刚度对连续啮合齿轮传动动态啮合特性的影响。

然而,上述研究中所采用的有限元分析方法,存在耗费资源大,不利于齿轮副的快速优化设计的缺陷。

研究人员结合有限元法和解析法的各自优点,提出了解析-有限元法。采用该方法可以快速计算齿廓修形、齿基、裂纹等多种参数下的齿轮时变啮合刚度。WANG Qi-bin等人[6]采用三维有限元法构建了齿基模型,并将该模型与基于势能法构建的轮齿副啮合刚度模型进行了刚性耦合,借此分析了裂纹对啮合刚度的影响规律。CHEN Kang-kang等人[7-8]运用解析—有限元法,分析了轮齿剥落对直齿和斜齿轮啮合刚度、接触应力和齿根圆角应力的影响;但该方法不能适应制造误差等新条件,需进一步研究扩大其应用范围。

由于求解效率高的特点,解析法被广泛应用于时变啮合刚度的快速计算中。TIAN Xin-hao[9]利用势能法和渐开线轮齿的特性,导出了健康直齿轮与裂纹、断齿直齿轮啮合刚度的表达式。WU Si-yan等人[10]在YANG D C等人[11]的研究基础上,将直齿轮模拟为基圆上的变截面悬臂梁,提出了综合考虑弯曲刚度、径向压缩刚度和赫兹接触刚度的直齿轮时变啮合刚度模型;但研究中并未考虑轮齿剪切变形、齿根圆角部分以及齿基对啮合刚度的影响。SAINSOT P等人[12]基于Muskhelishvili理论,提出了一种齿基刚度的解析公式。马辉等人[13]基于能量等效原理,提出了一种包含渐开线齿廓部分与齿根过渡曲线部分的直齿轮改进时变啮合刚度模型。CHEN Zai-gang等人[14-17]基于梁变形理论,提出了综合考虑抗弯刚度、剪切刚度、径向压缩刚度、赫兹接触刚度和齿基刚度的直齿轮时变啮合刚度模型,并分析了齿廓修形和裂纹对时变啮合刚度的影响。

然而,上述研究并未考虑多齿啮合对刚度叠加模型中齿基刚度的影响。因此,MA Hui等人[18-20]提出了一种多齿啮合状态下的齿基刚度改进计算式,并结合弹性力学原理分析了齿顶导圆和摩擦对时变啮合刚度的影响。除此之外,许多文献也研究了齿廓修形、点蚀、磨损、剥落、裂纹等因素对直齿轮时变啮合刚度的影响[21-24]。

然而,目前考虑齿向修鼓和轴向错位的直齿轮副时变啮合刚度激励的研究较少。这是由于该齿轮副在受载状态下将会由整个齿宽的线接触转换为局部共轭接触形成椭圆形接触区域。上述研究中的方法多是对轮齿整体进行受力分析,结合弹性力学原理求解应变能从而导出刚度计算式,对局部接触齿轮副则不完全适用。若采用WAN Zhi-guo等人[25]447-463提出的基于切片理论的累积积分势能法,计算齿向修鼓和轴向错位的直齿轮啮合刚度,则忽略了片齿间的耦合效应。

虽然YU W等人[26]在AJMI M等人[27]的研究基础上,提出了一种考虑片齿耦合效应的片齿加权因子分布模型;但是,该模型存在因子难以准确估算的缺点。此外,采用切片法计算齿向修鼓和轴向错位的直齿轮啮合刚度时,则需要通过TCA与LTCA计算接触点、接触迹线以及加载接触区,这是齿向修鼓和轴向错位的直齿轮副啮合刚度准确计算的前提,也是计算中的难点之一。

笔者针对齿向修鼓和轴向错位直齿轮副展开研究,提出一种改进的啮合刚度计算方法。

首先,在直齿轮误差模型的基础上,结合弹性力学理论计算加载状态下的啮合特征;然后,结合势能法以及切片理论,推导齿向修鼓和轴向错位直齿轮副改进时变啮合刚度解析式;最后,与有限元结果对比分析,对该解析模型进行验证;并分析不同鼓形量与错位量对直齿轮副啮合特性的影响。

1 直齿轮误差数学模型

鼓形齿示意图如图1所示。

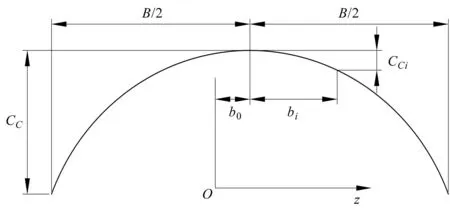
图1 鼓形齿示意图Fig.1 Tooth lead crown relief diagram注:B,Cc,Cci为齿宽、最大修形量和齿廓任意点修形量。

根据多项式函数,Cci表示为[28]1-9:

(1)

式中:s为曲线弯曲系数;b0,bi见文献[28]2-3。

轴向错位即直齿轮副的两平行轴线错位一个角度的示意图,如图2所示。

图2 作用面上的轴向错位Fig.2 Misalignment error on the action plane

图2中,Cmi是任意截面齿廓处的错位量;该错位量可以由小齿轮和大齿轮上的展角来定义,即:

(2)

式中:βb,θx,θy,ψ12等参数详见文献[28]3-4。

结合式(1)～式(2)可知,齿对的总误差Ei可表示为:

(3)

式中:上标(p),上标(g)为小轮与大轮。

2 齿接触分析及加载齿接触分析

考虑齿向修鼓和轴向错位的直齿轮副会由线接触转换为局部共轭接触,并在载荷作用下形成椭圆形接触区域。

瞬时接触特征如图3所示。

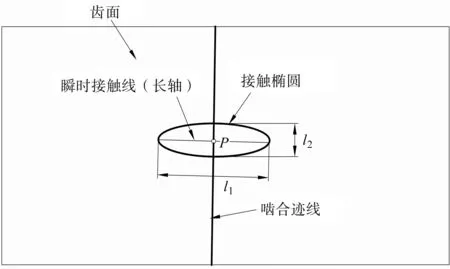
图3 接触特征示意图Fig.3 Contact characteristic diagram注:P为瞬时接触点;l1,l2为椭圆长轴与短轴长度。

图3中,齿面上各个瞬时接触点的连线即为啮合迹线。

TCA与LTCA技术的目标则是为了求解瞬时接触点P和椭圆主轴长l1、l2及其方向。

2.1 齿接触分析

局部共轭接触直齿轮副齿接触分析(TCA)如图4所示。

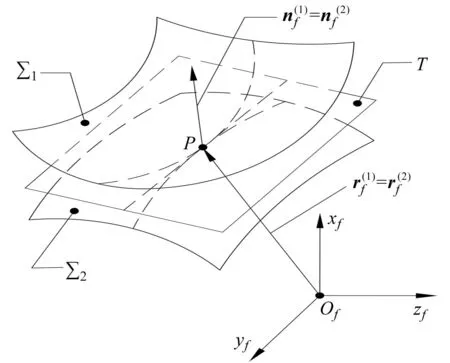
图4 TCA示意图Fig.4 TCA diagram注:为齿面∑1和∑2于坐标系Sf中的法矢和位置矢量;T为接触点P处的切平面。

图4中,设定坐标系S1和S2分别与主动轮和从动轮固连,坐标系Sf为全局固定坐标系,固定坐标系Sq表示装配错位。由于齿向修鼓直齿轮齿面不再是标准渐开线齿面,无法用渐开线函数准确表达齿廓特征。

为了TCA以及LTCA程序编写的简化以及程序的可计算性,笔者采用B-样条曲面将齿廓偏差齿面重新表征为双参数函数r(u,v)[29-30]。

齿面∑1和∑2的位矢和单位法矢在坐标系S1和S2中可表示为:

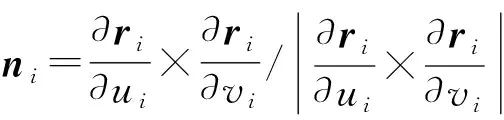
(4)

∑1绕Sf中的固定轴旋转。结合式(4),位置矢量和单位法矢在Sf中可表示为:

(5)

∑2则是绕错位坐标系Sq中的固定轴旋转,位置矢量和单位法矢在Sf中可表示为:

(6)

式中:L为3×3阶矩阵,可由矩阵M确定。

接触齿面于接触点处相切,此时两齿面的位置矢量和法矢满足下式条件:

(7)

式中:φ1为∑1绕自身轴线的旋转角度;φ2为∑2绕自身轴线的旋转角度。

其中:位矢方程提供3个标量方程,法矢方程提供2个标量方程,却有6个未知数,即u1,v1,φ1,u2,v2,φ2。

因此,给定一个参数v2,对式(7)提供的5个非线性方程进行迭代求解,便可得到另外5个参数,其对应的齿面点即为接触点;不同v2下的接触点连线即为接触路径,直到迭代点超出齿面范围。

2.2 加载齿接触分析

接触点P处的受载变形如图5所示。

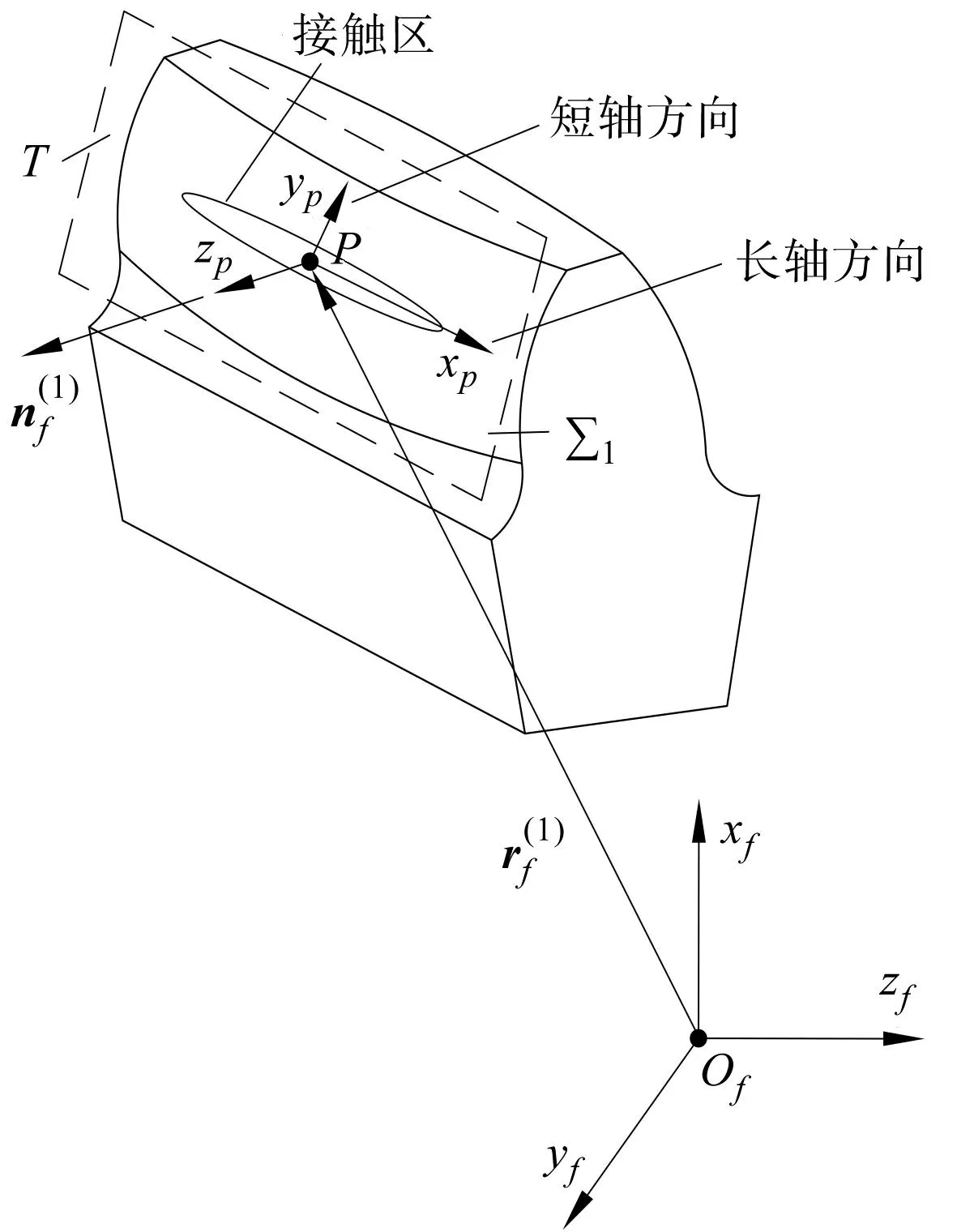
图5 切面坐标系示意图Fig.5 Section coordinate system diagram

对于标准直齿轮或者齿向修鼓直齿轮,椭圆主轴分别为齿长方向和齿廓方向。由于轴向错位的影响,主轴方向与主方向存在一定角度。

椭圆主轴与主方向示意图如图6所示。

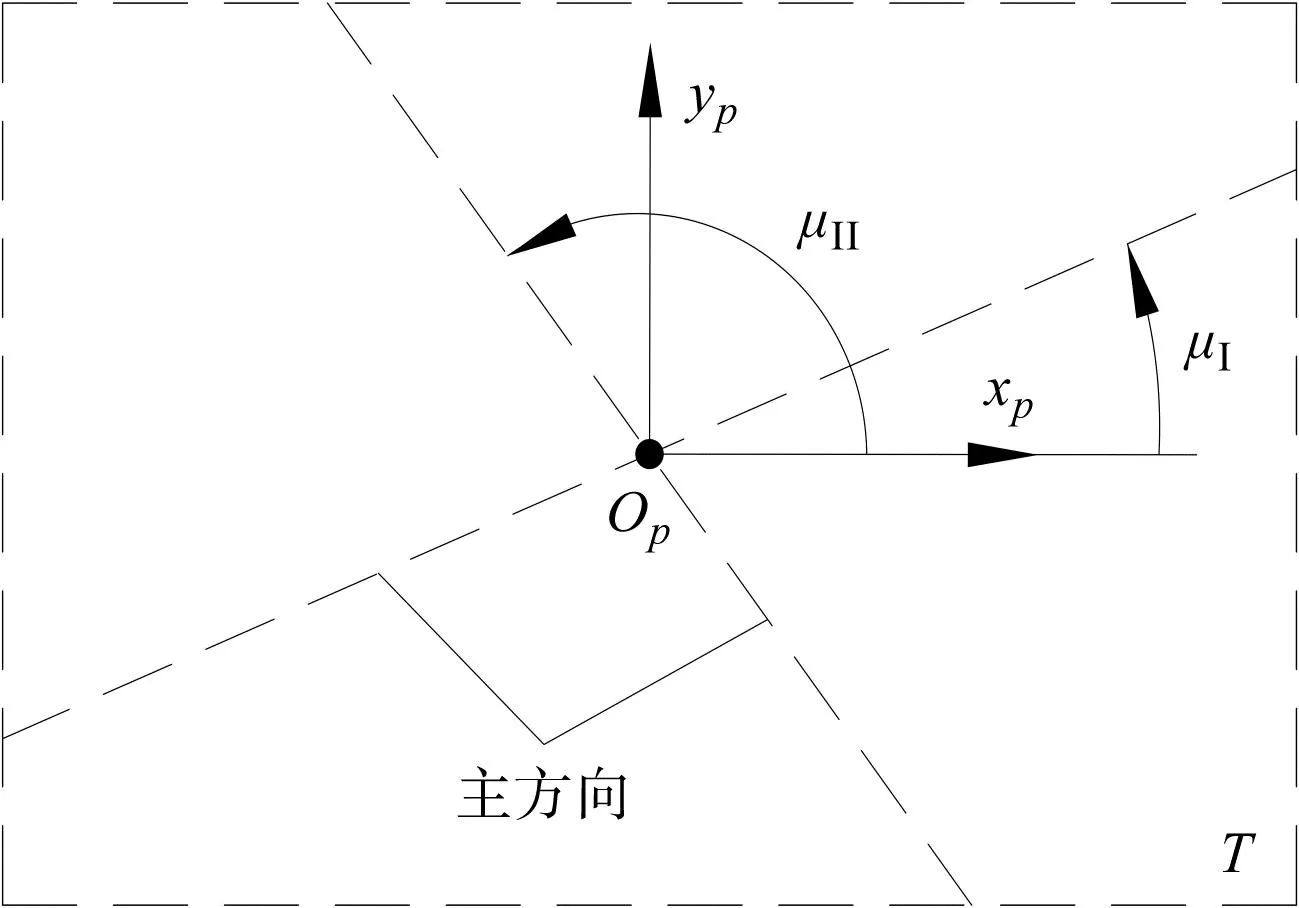
图6 曲率与主轴关系示意图Fig.6 Curvature and spindle relationship diagram注:μⅠ,μⅡ为椭圆主轴方向与主方向间的夹角。

根据欧拉公式,任意方向上的法曲率可表示为:

(8)

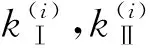
笔者结合式(8)可计算出两齿面的相对法曲率。其中,最大相对法曲率方向为椭圆短轴,最小相对法曲率方向为长轴[32];求得对应的曲率半径并结合赫兹理论,给出曲率半径与半长轴和半短轴间的关系为:

(9)

式中:a为椭圆半长轴;b为椭圆半短轴;E(e)为第二类完全椭圆积分;K(e)为第一类完全椭圆积分。

笔者在式(9)基础上,补充a和b的关系表示如下:

(10)

式中:F为法向啮合力;Re为等效曲率半径,值为(RⅠRⅡ)1/2;E*为等效弹性模量;f(e)为a/b相关的函数。

这些参数可表示为[33]:

(11)

式中:e为椭圆率;E为弹性模量;v为泊松比。

笔者结合式(9)～式(11),可得椭圆主轴长l1和l2。

3 时变啮合刚度模型

轮齿沿齿宽方向切片处理示意图如图7所示。

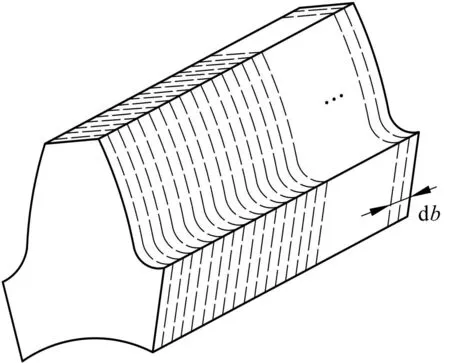
图7 切片示意图Fig.7 Slice diagram注:db为片齿宽度。

计算标准直齿轮结构刚度和赫兹接触刚度时需考虑整个齿面上的片齿。而对于齿廓偏差直齿轮副,则只需考虑接触区内片齿。

片齿等效变截面悬臂梁模型如图8所示。

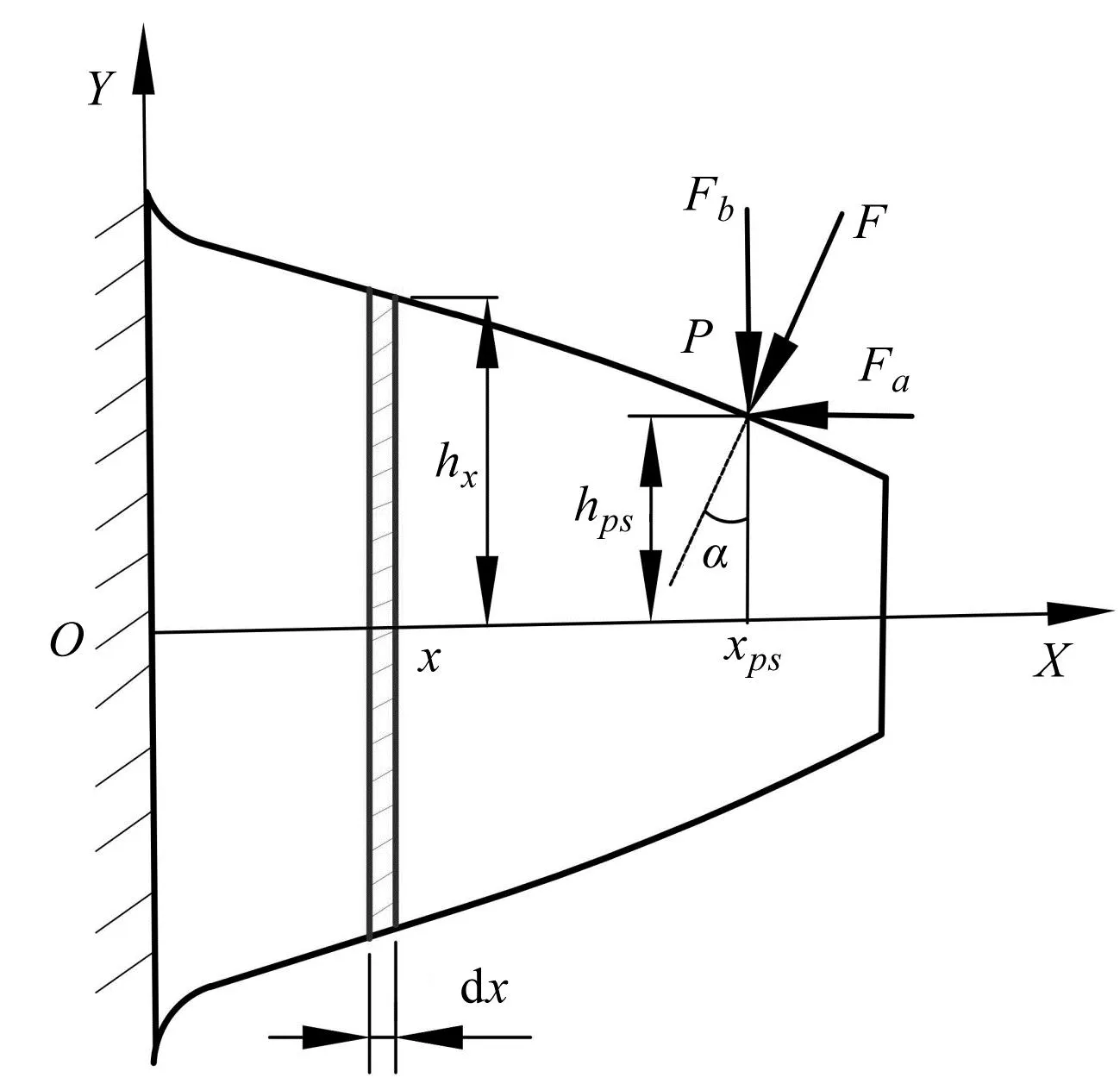
图8 悬臂梁模型Fig.8 Cantilever model注:F为法向啮合力;Fb,Fa为F的分力;xps,x分别为啮合点和变截面齿廓点处的横坐标,对应的纵坐标为hps和hx。

由于齿向修鼓后的直齿轮齿面点横纵坐标值无法用标准渐开线函数计算得到。结合2.1节重构的齿面新函数r(u,v),并改变齿长参数u,对轮齿进行切片,可以得到任意截面齿廓参数。在齿根与齿顶截面齿廓的中点处建立坐标系,通过位置矢量关系即可进一步得到任意截面齿廓点的横纵坐标值。

Fb和Fa可表示为:

Fb=Fcosα
Fa=Fsinα

(12)

采用势能法,片齿受载变形存储的弯曲应变能dUb、剪切应变能dUs,及轴向压缩应变能dUa可表示为:

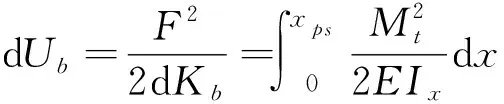
(13)

式中:Mt为力矩;Ix为惯性矩;Ax为截面面积。

这些参数可表示为:

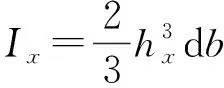
(14)

结合式(13)～式(14),片齿弯曲等效刚度dKb、剪切等效刚度dKs,以及轴向压缩刚度dKa可表示为:

(15)

赫兹接触刚度与非线性接触力有关,也呈非线性。在文献[34-35]中,作者采用有限元法和实验法都已对其进行了证实;因此,片齿赫兹刚度dKh表达式如下[36]:

(16)

式中:Fi为片齿载荷。

其中:Ee=2E1E2/(E1+E2)。

除轮齿刚度与赫兹刚度外,齿轮副啮合刚度中还包含齿基刚度。

齿基刚度Kf表达式如下[17]6:

(17)

式中:B为齿宽;系数L*,M*,P*,Q*以及参数uf和Sf详见文献[17]6。

由于齿向修鼓和轴向错位直齿轮副接触齿面间呈非线性接触,各片齿变形不同,力在片齿间的传递存在耦合效应。因此,笔者将各片齿以及片齿间的耦合效应等效为弹簧模型。

耦合效应等效弹簧模型如图9所示。

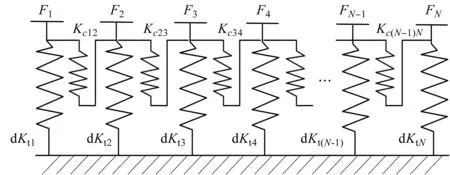
图9 片齿耦合弹簧模型Fig.9 Coupling spring model of slices注:dKti为片齿刚度;Kci(i+1)为耦合弹簧等效刚度。

结合式(15),Kci(i+1)可表示为[37]:

(18)

笔者将片齿刚度和耦合弹簧刚度用对角矩阵K表示,在力平衡原理的基础上,可得表达式如下:

F=K·δ

(19)

式中:F为片齿载荷矩阵;δ为片齿变形矩阵;矩阵F和δ中的元素分别是Fi和dδti。

根据力平衡原则,可得总的外力F表达式为:

(20)

在啮合力F作用下,齿轮副的片齿副变形示意图如图10所示。

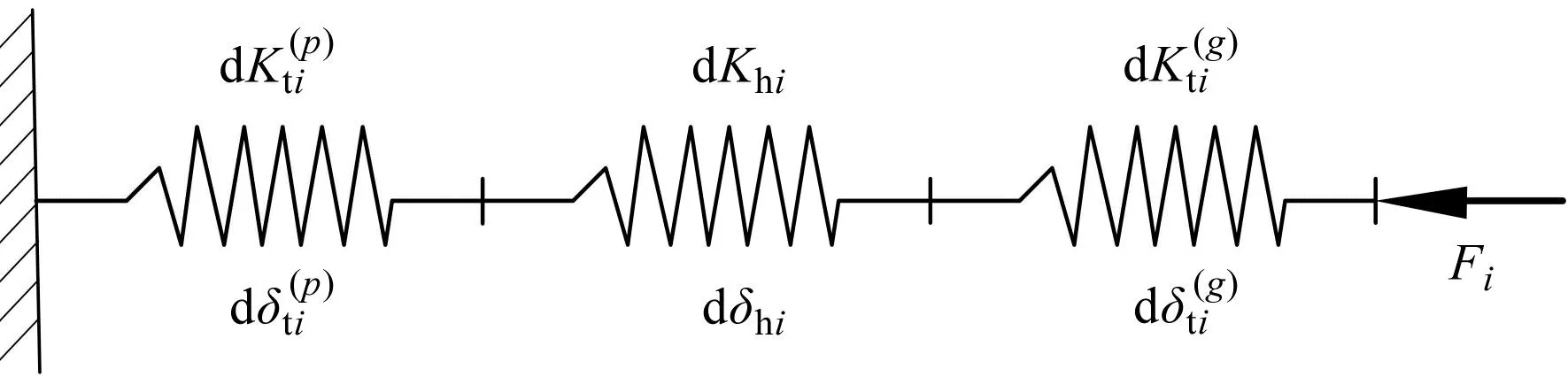
图10 串联弹簧模型Fig.10 Series spring model

根据串联弹簧理论,并结合式(16)、式(18),可得如下关系式:

(21)

式中:dδi为片齿副总变形。

结合式(21),可得片齿各变形分量关系如下:

(22)

结合式(18)～式(22)可以计算dδi,轮齿副总变形δ可表示为:

δ=Max(dδi),(i=1,2,…,N)

(23)

结合式(23),轮齿副总刚度K(pg)可表示为:

(24)

结合式(17),单齿啮合刚度Ke表达式为:

(25)

结合式(3),各片齿对之间的齿形误差可表示为:

E=[E1,E2,E3,…EN]T

(26)

结合式(19),当双齿啮合时,可得到如下表达式:

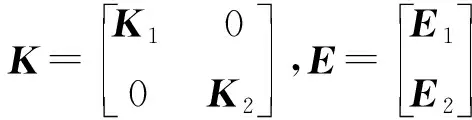
(27)

式中:角标1和2为齿对1和齿对2。

双齿啮合时,根据力平衡法则可得到:

F=F1+F2

(28)

式中:F1为齿对1啮合力;F2为齿对2啮合力。

只需设定初始载荷分配系数,根据式(28)即可得到各齿对的啮合力。同时,结合式(15),以及式(18)～式(22),即可计算各齿对的刚度矩阵以及变形列阵。综合式(26)～式(27),即可迭代出稳定的载荷分配系数。在此基础上,通过式(23)～式(25)计算,即可得到各接触对的单齿啮合刚度Ke。

传统多齿啮合刚度计算方法如图11所示。

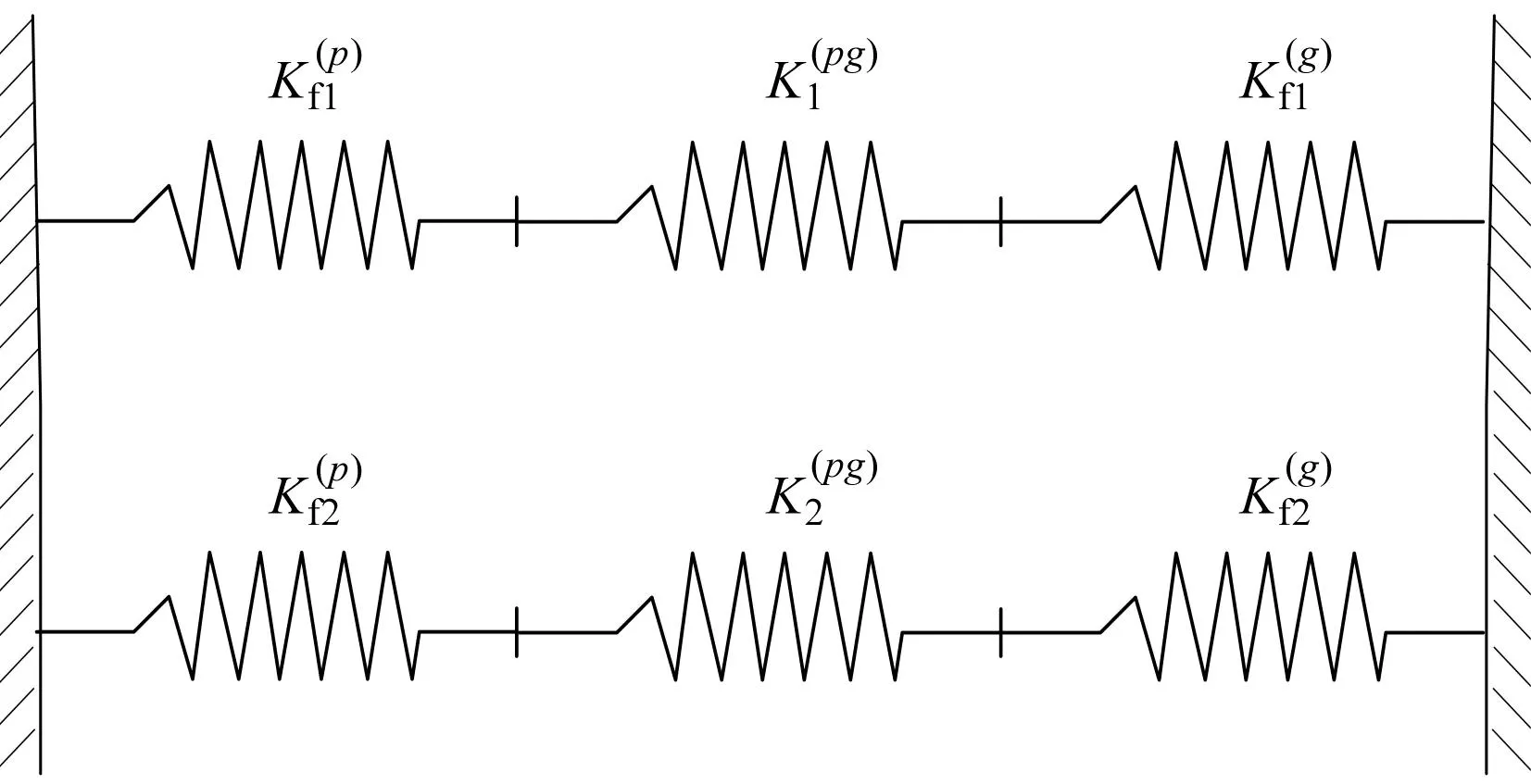
图11 多齿啮合齿基刚度传统计算方法Fig.11 Traditional method of multi-tooth meshing foundation stiffness

根据图11所示并联刚度模型,多齿啮合刚度K可以表示为:

(29)

式中:n为啮合齿对数。

实际上,两齿对啮合时,多齿共享一个齿基。

MA Hui等人[19]66-67提出了一个改进的多齿啮合齿基刚度计算方法。

多齿啮合齿基刚度改进模型如图12所示。

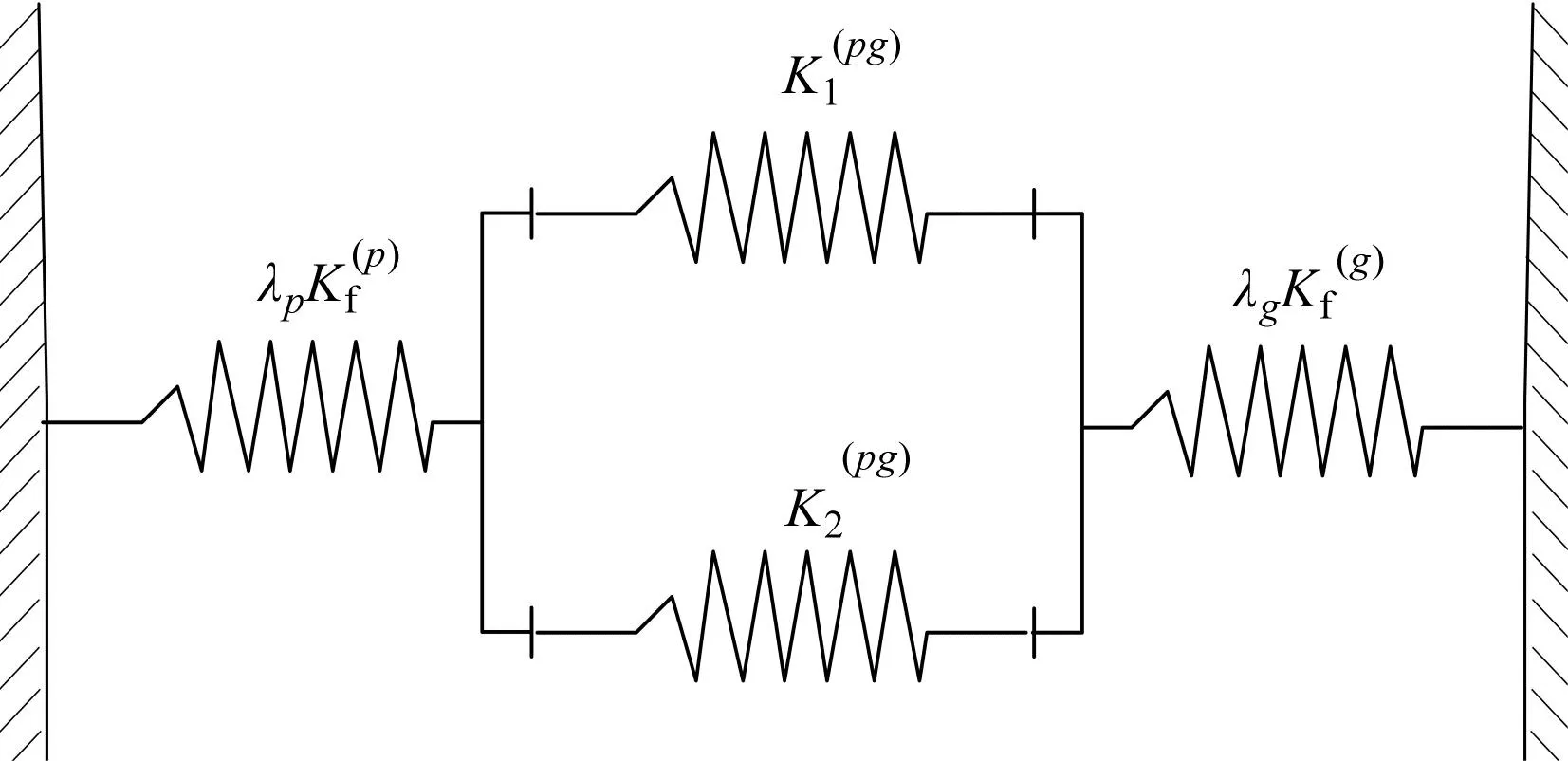
图12 多齿啮合齿基刚度改进计算方法 Fig.12 Improved method of multi-tooth meshing foundation stiffness

图12中,λ为齿基刚度的修正系数。单齿啮合时λ等于1;多齿啮合时,利用有限元法可以得到λ,具体计算流程见文献[19]66-67。

改进后的多齿对啮合齿基刚度可表示为:

(30)

笔者结合式(25)、式(29)、式(30),可得改进的多齿啮合刚度K表达式为:

(31)

4 验证与分析

通常来说,采用实验法对齿轮副啮合刚度的计算是最符合实际的。然而,进行实验需要昂贵的特殊设备,且易受到安装误差和设备测量精度等外部条件影响。因此,有限元法被许多研究者采用,这种方法可以自动考虑实际齿形误差的影响。

笔者采用文献[38]的有限元分析方法进行齿轮副静力学分析,以完成解析模型验证。齿轮内孔施加耦合约束,并添加相应边界与载荷条件;接触面之间通过接触单元进行耦合,接触行为为标准接触;分析过程不考虑动力学效应;施加扭矩为100 Nm。

用于实例验证的直齿轮参数如表1所示。

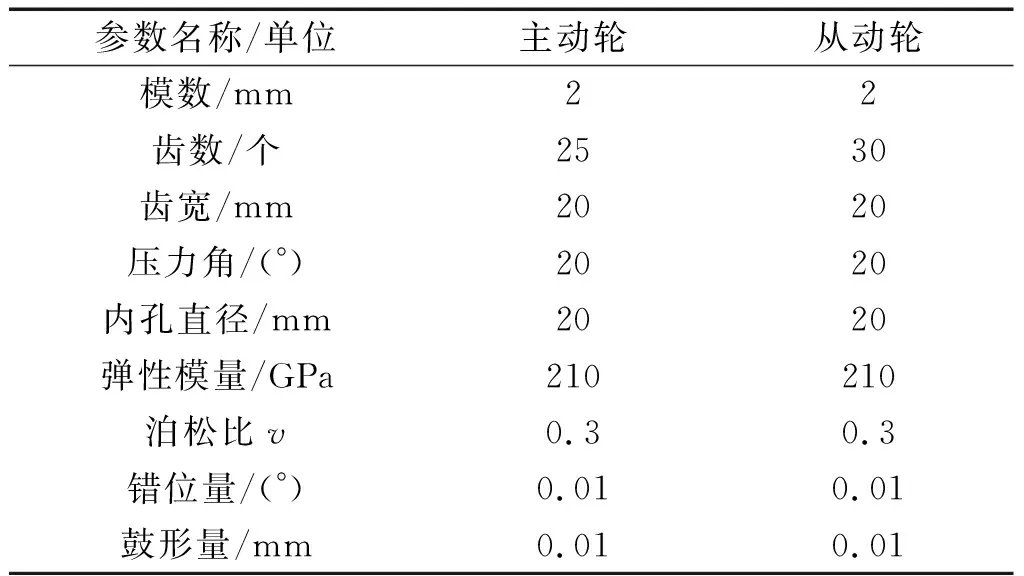
表1 基本参数Table 1 Parameters

4.1 模型验证

4.1.1 理想齿廓刚度比对

基于表1参数,笔者运用有限元法计算得到齿基刚度修正系数λ为1.19。

笔者运用上述齿向修鼓和轴向错位直齿轮副刚度计算方法,对齿向修鼓量和轴向错位量为0时的理想齿廓直齿轮副时变啮合刚度进行计算,并将其结果与文献[25]450-452的累积积分势能法和有限元法计算结果进行对比,如图13所示。

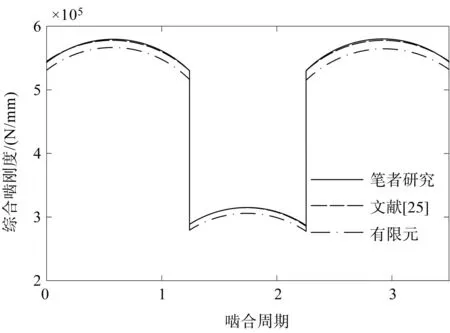
图13 时变啮合刚度对比Fig.13 Comparison of time-varying mesh stiffness注:实线、虚线、点画线为笔者提出的啮合刚度计算方法、文献[25]方法以及有限元法的啮合刚度曲线。

从图13中可以看出:采用3种方法得到的计算结果非常接近,曲线的变化趋势一致;运用笔者提出的啮合刚度计算方法计算理想齿廓直齿圆柱齿轮的时变啮合刚度与采用文献[25]方法的计算结果相同,这是由于理想齿廓直齿轮副各片齿间的变形相同,片齿间没有力的传递,说明运用笔者所提出的考虑片齿耦合效应的直齿轮副啮合刚度计算方法和不考虑耦合效应的累积积分势能法都能适用于理想齿廓直齿轮刚度计算。

从数值上看,基于笔者提出的啮合刚度计算方法所计算得到的时变啮合刚度均值为483 kN/mm,基于有限元法的结果为473 kN/mm,误差为2.1%;由此可以说明,笔者提出的齿向修鼓和轴向错位直齿轮副刚度计算方法对齿向修鼓量和轴向错位量为0的理想齿廓直齿轮副时变啮合刚度计算有较高的计算精度。

4.1.2 误差直齿轮副刚度比对

笔者基于表1参数,得到了综合考虑轴向错位量0.01°、鼓形量0.01 mm时的接触迹线以及接触区域计算结果,如图14所示。

图14 接触迹线以及接触区域对比Fig.14 Contact trace and contact area comparison

图14(a)是运用笔者提出的TCA及LTCA技术计算得到的接触迹线和椭圆长轴,黑色虚线表示椭圆长轴,黑色实线和黑色实心点分别表示接触迹线以及不同瞬时时刻的接触点。

图14(b)是有限元计算结果,云图区域则是实际承载接触区,图中标记的黑色实线表示接触迹线。经对比可知,两种方法的计算结果相近;接触点、接触线以及接触范围的准确计算也为后续的啮合刚度模型建立打下基础。

在此基础上,笔者分别运用提出的方法、文献[25]方法以及有限元法,对该错位量与鼓形量下的直齿轮副时变啮合刚度分别进行计算。

具体的时变啮合刚度结果对比如图15所示。

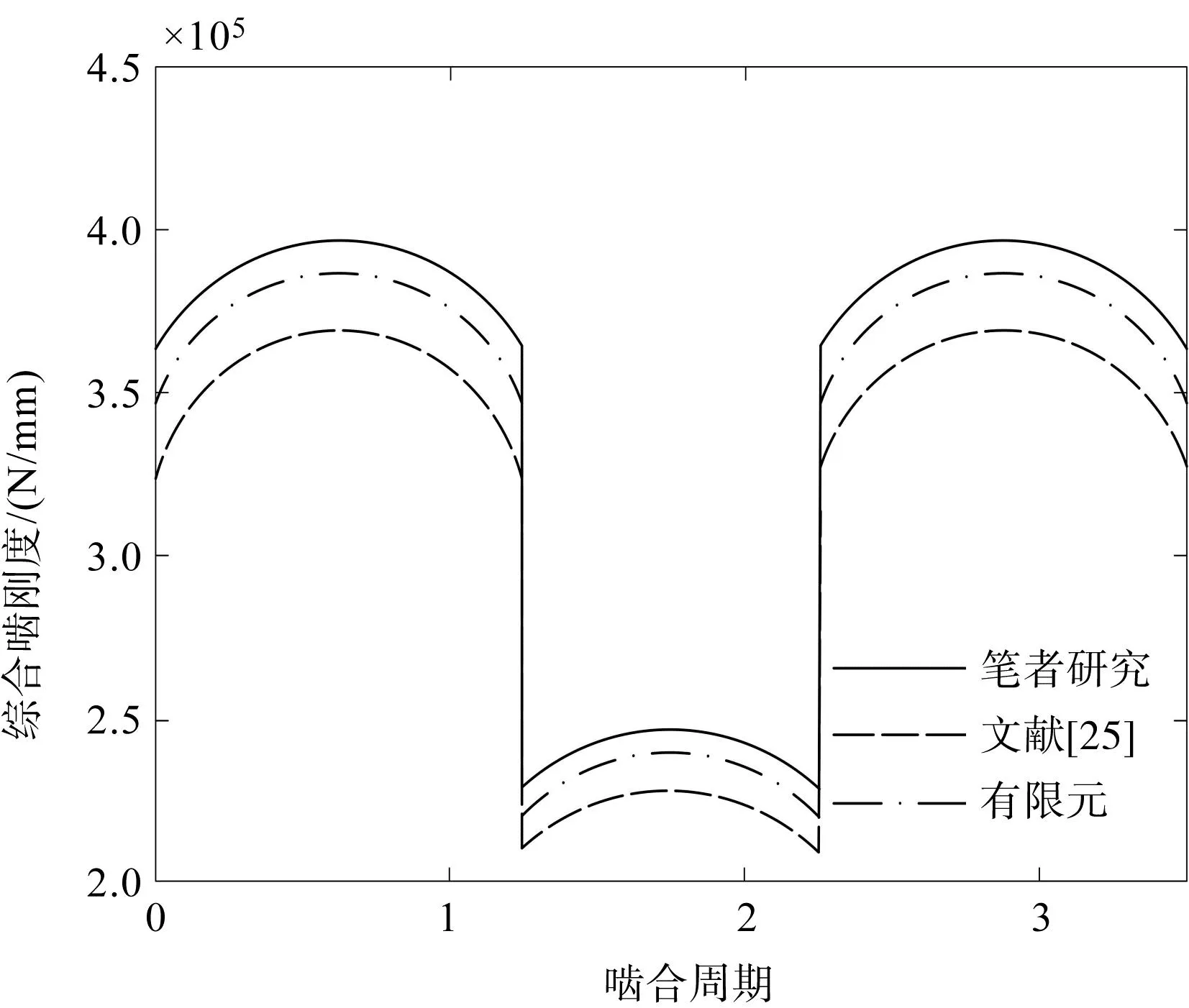
图15 时变啮合刚度对比Fig.15 Comparison of time-varying mesh stiffness

由图15可知:运用笔者提出的齿向修鼓和轴向错位直齿轮副刚度计算方法计算得到的啮合刚度结果略高于有限元结果,文献[25]方法的计算结果略低于有限元;从数值上看,运用笔者提出的齿向修鼓和轴向错位直齿轮副刚度计算方法计算得到的时变啮合刚度均值为339 kN/mm,文献[25]450-452方法的刚度均值为315 kN/mm,有限元的刚度均值为329 kN/mm,两者与有限元结果的误差分别为3%和4.2%;由此可以看出,笔者提出的齿向修鼓和轴向错位直齿轮副刚度计算方法的计算结果精确度高于文献[25]方法的计算结果的精确度。

以上结果说明,对于齿面间存在非线性接触的齿轮副,运用微元法对轮齿进行切片处理计算时变啮合刚度时(由于各片齿变形不同导致片齿间有力相互传递),考虑此片齿间耦合效应的时变啮合刚度计算方法的计算精度要略高于不考虑片齿耦合效应的累积积分势能法的计算精度[39-41]。

除此之外,相较于理想齿廓,考虑齿向修鼓和轴向错位后的齿轮副刚度均值降低了30%,可以看出齿向修鼓和轴向错位对齿轮副的刚度有较大的影响。

4.2 误差对啮合刚度的影响分析

4.2.1 错位量对啮合刚度的影响

基于表1参数,笔者将轴向错位量分别设置为0.01°、0.02°、0.03°、0.04°,得到了不同错位量的啮合刚度计算结果,如图16所示。

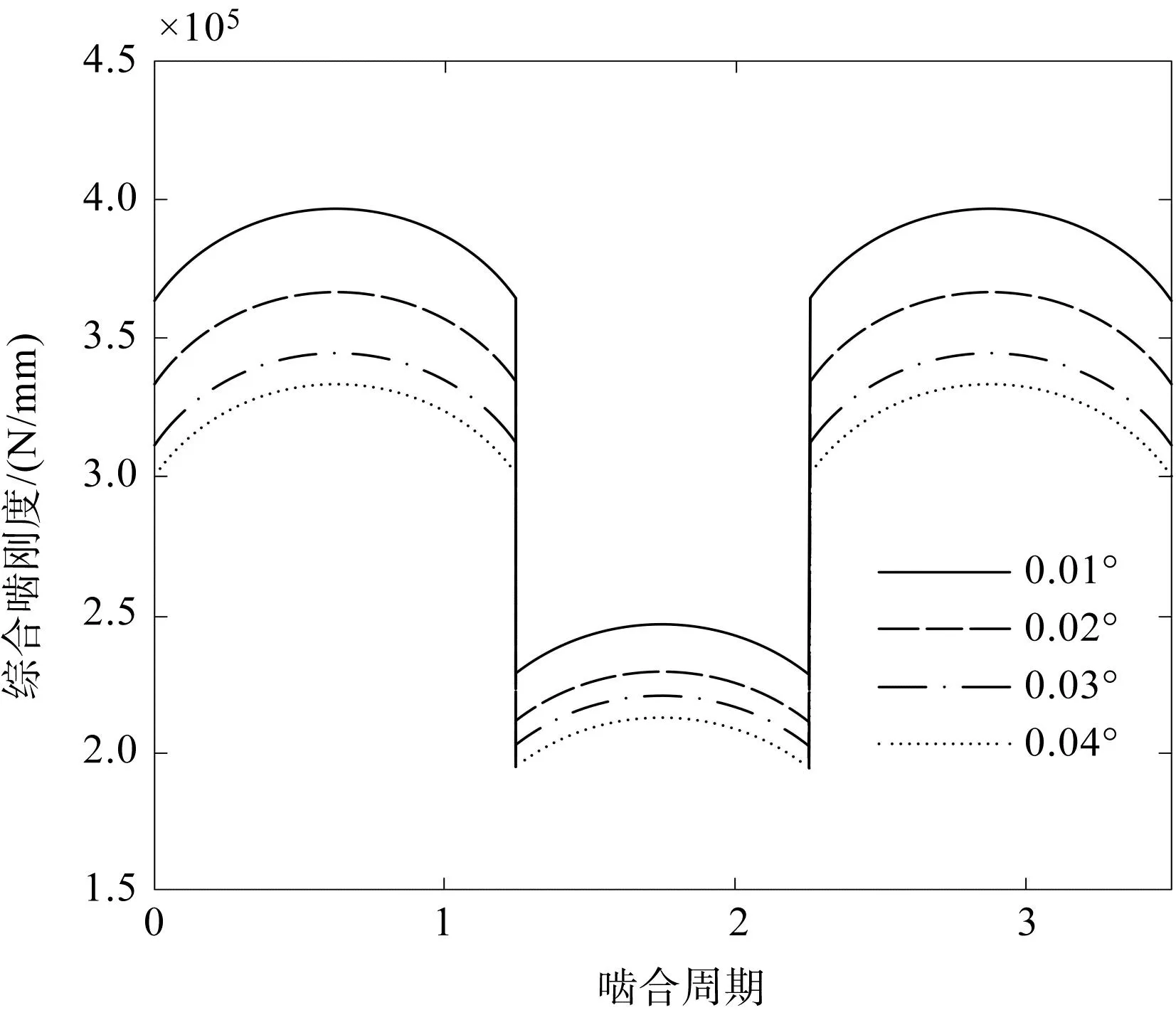
图16 不同错位量的啮合刚度Fig.16 Mesh stiffness with different misalignments

从图16中可以看出:随着错位量的增大,啮合刚度显著减小,呈负相关;这是由于错位量增大,接触区逐渐从齿面中部向齿端偏移,受曲率的影响,使得参与啮合的轮齿范围减小,即接触长轴逐渐减小,进而导致轮齿几何刚度、非线性赫兹接触刚度以及综合啮合刚度减小。

从曲线的变化规律上看,刚度的变化与错位量间并无明显的线性关系。在实际装配或者工程应用中,难以避免地会造成错位量。

因此,对错位状态下的齿轮副啮合刚度或者动力学特性进行分析时,错位量的影响不可忽略。

4.2.2 鼓形量对啮合刚度的影响

基于表1参数,在鼓形量分别为10 μm、15 μm、20 μm、25 μm时,可以得到啮合刚度的计算结果,如图17所示。

图17 不同鼓形量的啮合刚度Fig.17 Mesh stiffness with different lead crown reliefs

从图17中可以看出:时变啮合刚度随着鼓形量的增大而减小,呈负相关;这是由于鼓形量的增大会导致曲率增大、曲率半径减小,进而使承载状态下的椭圆接触区范围减小,参与啮合的轮齿部分减少,导致几何刚度、非线性赫兹接触刚度以及综合啮合刚度减小。

从曲线的变化趋势上看,啮合刚度的变化与鼓形量并无明显的线性关系,该结果说明,对齿向修鼓的齿轮副时变啮合刚度以及动力学特性进行分析时,不能忽略该参数的影响。

综上所述,考虑轴向错位以及鼓形量导致的齿轮副局部共轭接触,受载状态下会产生椭圆形的变形区域;不同的错位量、鼓形量会造成不同的接触特征,从而影响轮齿几何刚度、片齿耦合刚度以及赫兹接触刚度。

然而从图16～图17中可看出,这种影响规律目前无法用一个公式或者影响系数的泛值来表示,因为这种影响并无明显的线性可言。

5 结束语

笔者在直齿轮齿向修鼓和轴向错位模型的基础上,结合弹性力学理论计算了加载状态下的啮合特征;然后,结合势能法以及切片理论,推导了齿向修鼓和轴向错位直齿轮副改进时变啮合刚度的解析式;最后,将其与有限元结果进行了对比分析,验证了解析模型的有效性;并分析了不同鼓形量和错位量对直齿轮副啮合特性的影响。

研究结果表明:

1)理想齿廓下的齿轮副,由于接触线上的载荷分配均匀,片齿间没有力的传递,考虑耦合效应与不考虑耦合效应,运用累积积分势能法均能获得准确的计算结果;

2)基于提出的TCA与LTCA技术能够准确计算齿向修鼓和轴向错位直齿轮副瞬时接触点、接触迹线以及加载接触范围等啮合特征,是准确构建啮合刚度模型的前提;

3)运用微元法对轴向错位及齿向修鼓齿轮副时变啮合刚度进行计算时,考虑片齿耦合效应的计算结果略大于有限元结果,不考虑耦合效应采取累积积分势能法的计算结果小于有限元结果;前者计算精度更高,误差为3%。因此,提出的齿向修鼓和轴向错位直齿轮副刚度计算方法能够有效、精确地对齿向修鼓和轴向错位直齿轮副刚度激励进行求解;

4)轴向错位与鼓形齿都会对啮合刚度有显著影响,增大轴向错位与鼓形量均会造成轮齿几何刚度、赫兹接触刚度以及综合啮合刚度减小;但是,这种影响并无明显的线性规律。因此,在对齿轮副啮合刚度的分析以及动力学特性进行研究时,不可忽略轴向偏差以及鼓形量的影响;

5)对于考虑修形、轴向错位等的局部接触斜齿轮以及锥齿轮副等,啮合刚度计算中若采用切片法,需考虑片齿间的耦合效应;此外,提出的齿向修鼓和轴向错位直齿轮副刚度计算方法也可进一步推广到局部接触齿轮副的啮合刚度计算中,为齿轮副动力学模型的构建和分析提供理论基础。

由于实际啮合过程中,受载导致支撑构件变形,啮合副会发生轴向错位。因此,在后续的研究中,笔者将以啮合激励为切入点,构建多部件柔性耦合动力学模型,以激励波动趋势为参量标准,有效进行齿向修鼓等齿面修形优化。