农林作业机械静液压传动系统效率特性建模及减速比分析*

程 准,邢 杰,李文杰

(南京林业大学 汽车与交通工程学院,江苏 南京 210037)

0 引 言

农林作业机械类型众多,例如拖拉机、联合收获机、联合采伐机、林果采摘机等。农林作业机械主要行驶于松软土路面,行驶时负载阻力大且不稳定,工况多变[1-3]。

由内燃机、静液压传动系统和机械齿轮装置等组成的驱动与动力传动系统被广泛应用于农林作业机械[4-6]。静液压传动系统常用变量泵和定量马达,其控制系统简单,采用容积调速回路易于实现较大范围内的无级调速[7-8]。然而,静液压传动系统的传动效率有限,普遍低于齿轮变速传动装置[9-11]。因此,设计阶段考虑静液压传动系统工作效率,评估分析整机能耗,具有重要意义。

周冉等人[12]对轮式采伐机底盘行走机构进行了分析与设计,通过对采伐机在林区地面行驶时负载工况的计算,对液压系统元件进行了选型,并采用AMESim搭建了仿真模型,以验证设计方案的有效性,该方法能有效提高设计效率;但其仿真模型结果存在一定程度的潜在误差。任军华等人[13]通过台架试验测量,获取了不同油门开度和发动机转速下液压系统的传动效率,并进行了发动机与静液压传动系统的联合优化分析,该研究为农业机械使用过程中全系统能耗的改善提供了有价值的参考;但其未具体建立有明确表达式的数学计算模型,不便于变速系统的设计和控制。LIU Z J等人[14]对山地履带式拖拉机的静液压传动系统进行了匹配设计,搭建了驱动系统的测试台架,进行了牵引性能和起步加速性能等测试,验证了设计方案的有效性;但研究未深入考虑液压传动系统的工作效率。KIM D M等人[15]针对静液压传动系统工作时的一种特殊现象,基于Simulation X开发了分析模型,并利用试验测试进行了探究;但研究未具体涉及液压系统或拖拉机整体传动系统工作效率的影响情况。朱镇等人[16]建立了泵控马达系统的效率模型,分析了泵控马达系统的高效率工作区间,采用公式拟合法获取了泵与马达效率的计算表达式。孙景彬等人[17]采用泵-马达调速回路设计了山地拖拉机的传动系统(其动力传递路线大致为:发动机—离合器—分动箱—静液压传动装置—驱动后桥),但在传动系设计阶段,未充分考虑实际液压系统效率特性(根据液压泵和液压马达的工作特性建立与实际相符的效率特性模型是其关键)。

由于泵和马达的效率变化呈非线性,其模型参数数量较多,在取值范围未知的情况下辨识难度大。此外,马达至驱动轮之间减速装置的传动比对整机能耗的影响值得进一步探究,为设计阶段提供决策性帮助。

笔者以某农林作业机械为例,对其传动系进行匹配设计,针对已选液压系统,提出一种决策变量自适应变化的效率特性参数辨识方法,即根据实测试验数据,采用内层循环(蒙特卡罗法)的随机投点搜寻各待辨识参数的最优解,采用外层循环调节各待辨识参数的搜索区间;基于已建立的整机调速特性和效率特性模型,分析减速器传动比设计值对整机传动系能耗的影响。

1 农林作业机械动力传动系统

1.1 传动原理

笔者采用的农林作业机械动力传动方案示意图如图1所示。

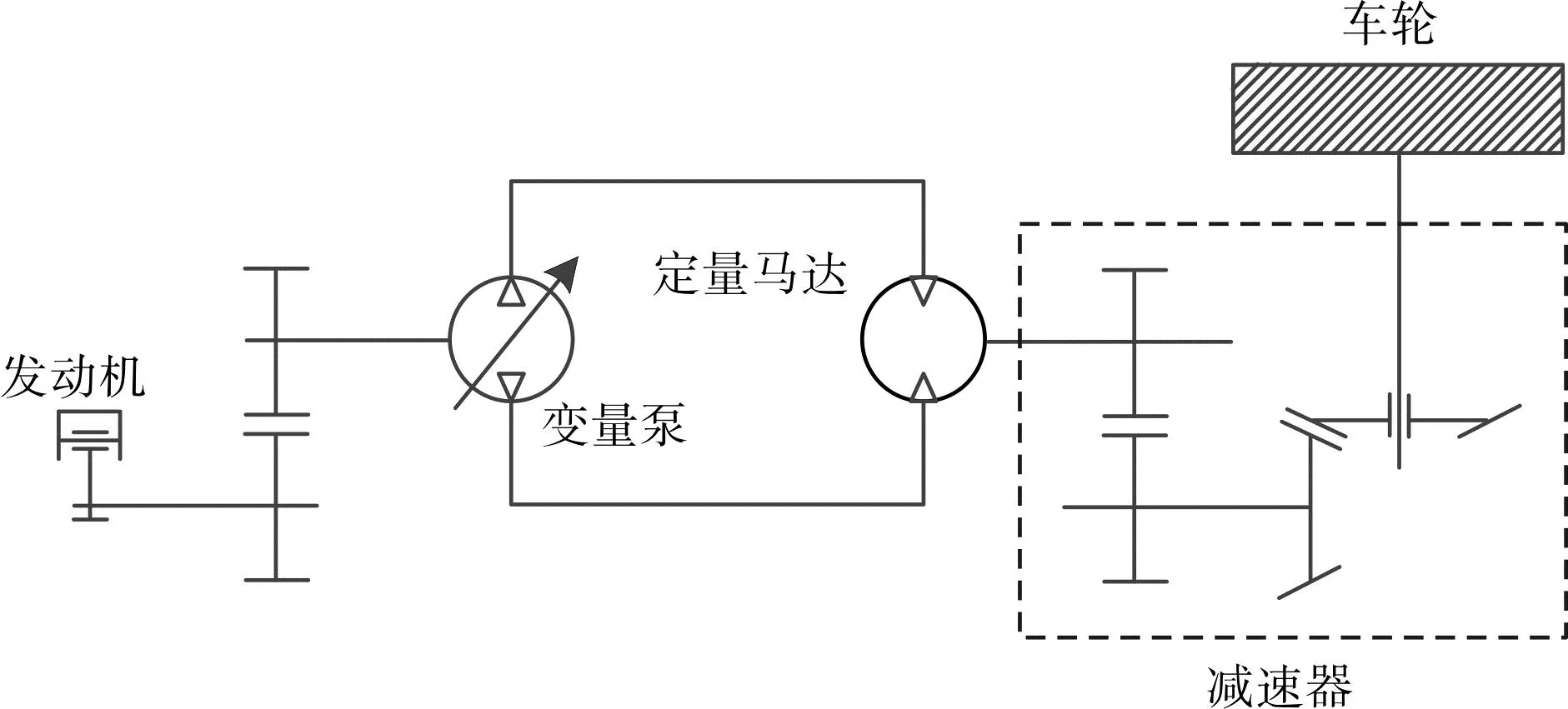
图1 一种农林作业机械动力传动方案Fig.1 A power transmission scheme of agricultural and forestry machinery

图1中,动力传动系统主要由静液压传动系统(变量泵驱动定量马达、容积调速回路)、双级减速器(第一级为圆柱齿轮、第二级为锥齿轮)、差速器、半轴等组成。

其动力传动路线为:发动机—一级圆柱齿轮(用以匹配调节发动机和变量泵之间的转速和转矩)—变量泵(通过排量调节马达转速)—定量马达—双级减速器—驱动轮。

1.2 整机调速特性

此处静液压传动系统的速度控制回路采用容积调速回路,忽略液压回路泄漏,变量泵转速np和定量马达转速nm的关系表达式如下:

nm=npVp/Vm

(1)

式中:Vp为变量泵的排量;Vm为定量马达的排量。

根据动力传递路线推导整机调速特性,计算表达式如下:

(2)

式中:ua为整机行驶速度;0.377为单位换算系数;rd为驱动轮半径;im为双级减速器-第一级圆柱齿轮传动比;i0为双级减速器-第二级锥齿轮传动比。

综合式(1)和式(2)可知:控制变量泵转速和排量即可实现农林作业机械整机行驶速度的无级调节目的。

1.3 整机效率特性

变量泵-定量马达系统的总效率特性数学模型常用式(3)和式(4)的乘积来表示,具体如下[16,18]:

(3)

(4)

式中:np为变量泵转速;Δp为系统压力差;ε为排量比(即变量泵的当前排量与最大排量之比[16],笔者取变量泵的最大排量和定量马达排量一致);Cs为层流泄漏系数;Cv为层流阻力系数;μ为液压油动力黏度;Cf为机械阻力系数;ηp为液压泵效率;ηm为液压马达效率。

由于容积调速回路中系统压力差基本由负载转矩决定,当动力传动系统工作稳定时,系统压力差与负载转矩呈正相关。负载转矩主要由农林作业机械行驶时所受阻力决定,其关系表达式如下:

Tm=Frrd/(i0im)

(5)

式中:Tm为定量马达输出轴扭矩;Fr为整机阻力。

由整机的动力传递路线可知,整机传动效率主要与静液压传动系统工作效率和3组齿轮传动效率有关。齿轮传递动力时,过程平稳,其传动效率常设为固定值[19-20]。

因此,整机传动效率可被描述为以变量泵转速、定量马达输出轴扭矩和排量比为自变量的数学函数表达式,具体如下:

(6)

式中:ηT为整机传动效率;ηg为齿轮传动效率。

其中:a1～a6与层流泄漏系数、层流阻力系数、液压油动力黏度以及机械阻力系数等参数有关,由液压系统的实际试验数据辨识后确定。

2 整机动力需求计算及液压系统选型

笔者以停车作业的林果采摘机械为例,整机于松软土路面上行驶时主要受坡度阻力和滚动阻力作用。其中,滚动阻力主要由轮胎弹性迟滞所引起的变形阻力、土壤压实阻力和推土阻力组成。

笔者借助KURJENLUOMA J等人[21]的研究,采用经验公式对滚动阻力进行估计,计算表达式如下:

Ff=(b1Z+b0)mg

(7)

式中:Ff为滚动阻力;Z为滑转沉陷量;b0,b1为经验系数,分别取值0.098 8和0.001 3;m为整机质量;g为重力加速度。

滑转沉陷量的计算表达式[22]如下:

(8)

式中:W为轮胎法向载荷;kc,kφ为土壤黏聚变形模数和摩擦变形模数;b,D为轮胎宽度和直径;s为车轮滑转率;n为沉陷指数。

坡度阻力计算公式如下:

Fi=mgsinα

(9)

式中:Fi为坡度阻力;α为坡度角。

整机主要参数如表1所示。

表1 整机主要参数Table 1 Main parameters of the machinery

笔者以表1所列参数的取值为例,根据农林作业车辆于水平路面上最高行驶速度和最大爬坡工况匹配计算整机最大需求功率,计算得到上述2种工况下整机最大需求功率分别为73.14 kW和71.03 kW;选择林德液压HPV-02系列液压泵(最大排量为55 cm3/r、额定压力为420 bar、持续功率为75 kW)和HMV-02系列液压马达(最大排量为55 cm3/r、额定压力为420 bar、持续功率为93 kW)。

笔者采用式(2)计算求得双级减速器总传动比≤19.66。

3 基于改进蒙特卡罗法的参数辨识

3.1 蒙特卡罗法的改进

枚举法、启发式优化算法和蒙特卡罗法(MCM)[23-24]常用于优化、求解和参数辨识等场合。MCM采用随机投点方式,相较于枚举法,其收敛精度高、算法执行次数少;相较于启发式优化算法,其可有效避免早熟现象。

因此,笔者选择MCM作为静液压系统效率特性模型参数辨识方法。

枚举法、启发式优化算法和MCM普遍对决策变量的定义域(即取值范围或搜索范围)有很大程度的依赖。式(6)为变形后的系统效率特性数学表达式,待辨识参数a1～a6的定义域未知,静液压系统效率特性模型参数辨识困难。

因此,笔者提出I-MCM法,以自适应决策变量的搜索范围。该算法采用内层循环和外层循环,其主要步骤如下:

步骤1。初步设置待辨识参数的搜索范围。在此阶段,可设置搜索范围为任意常数,且统一设置全部待辨识参数的搜索范围;

步骤2。运算内层循环。内层循环采用标准蒙特卡罗法,通过随机投点的方式形成任意1组6个待辨识参数的随机方案,对每1组方案以目标函数为评价指标进行比对,最终以优胜劣汰的原则确定6个待辨识参数的数值。

目标函数如下:

(10)

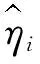
步骤3。运算外层循环。外层循环基于每一次内层循环的参数辨识结果,自适应调节每个待辨识参数在下次内层循环中的搜索范围,搜索范围调整函数如下:

(11)

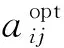
3.2 静液压系统效率特性模型参数辨识

已选液压泵和液压马达的实际工作效率由试验台架测得。

台架示意图如图2所示。

图2 静液压传动系统台架示意图Fig.2 Hydrostatic transmission system bench diagram

图2中,该实际系统定量马达的输出端通过双级减速系统与电涡流测功机相连,因此其传动形式与对象基本一致。

效率计算所需的决定性物理量(输入转速、输出转速、输入转矩和输出转矩)测量结果如图3所示(在任意工况下,重复进行5次试验)。

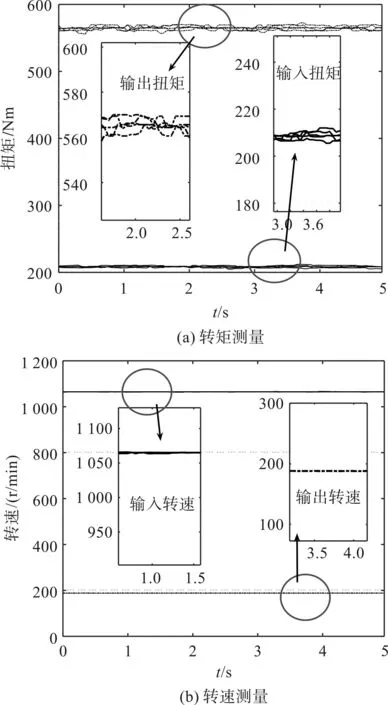
图3 重复性试验测量结果Fig.3 Repeatability test measurement results

图3中,输入转速、输出转速、输入转矩和输出转矩的重复性精度良好,标准差分别为0.41 r/min、0.24 r/min、0.97 Nm、2.77 Nm,测量不确定度和误差相对较小。

试验台架其余相关信息及效率试验测量过程与结果见文献[25],泵输入转速在500 r/min～3 000 r/min范围内取5水平,马达输出转矩在50 Nm～500 Nm范围内取5水平,泵排量比在0.17～1.00范围内取5水平。文献[25]采用组合试验的方法,获取共计15组试验样本数据。

笔者采用改进I-MCM进行静液压系统效率特性模型的参数辨识,设置外层循环迭代次数为30,内层MCM运行次数为10 000,6个待辨识参数的初始搜索范围为0～10。由于算法具有一定的随机性,笔者重复进行5次参数辨识试验。

5次重复性试验中,目标函数值的迭代运算结果如图4所示。

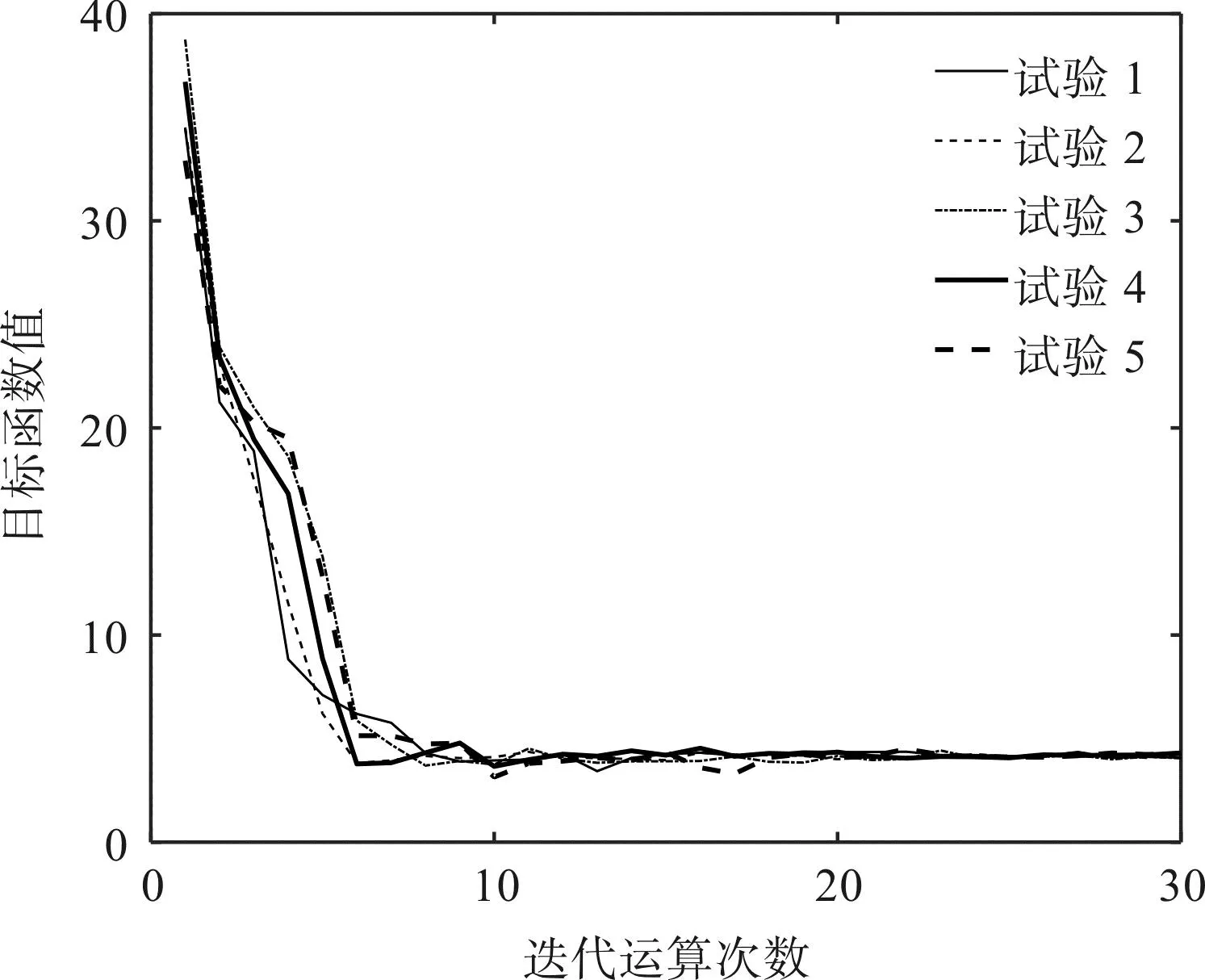
图4 参数辨识重复性试验结果Fig.4 Repeatability test results of parameter identification

图4中,5次重复性参数辨识结果具有相似性,外层循环约第10代已收敛至最优解,平均绝对百分比误差(即目标函数值)的均值为4.19%。参数辨识结果为a1=82.987 3、a2=0.335 2、a3=3.153 5×10-7、a4=3.041 1×105、a5=4.236 1×103、a6=0.159 8。

6个待辨识参数的取值差异性较大,其中a1、a4和a5不在初始搜索范围内,而a2、a3和a6则仅处于初始搜索范围的边缘位置,这表明该例参数的辨识具有一定的难度[26]。

基于I-MCM的参数辨识结果如图5所示。

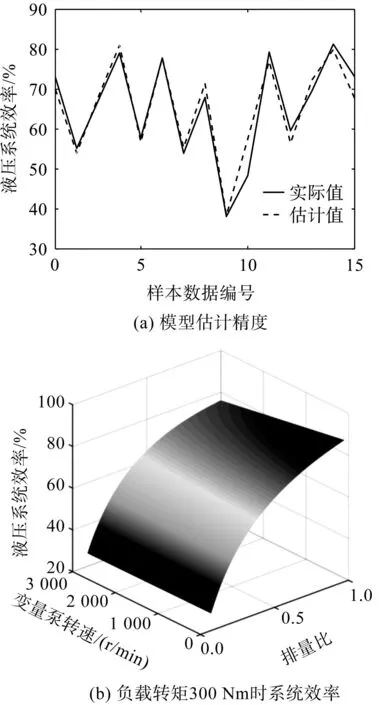
图5 基于I-MCM的参数辨识结果Fig.5 Parameter identification results based on I-MCM

图5(a)为参数辨识后液压系统效率模型估计值与实际值的对比。图5(b)为负载转矩固定为300 Nm时,液压系统效率特性模型的估计结果。

图5中,笔者采用I-MCM对模型参数辨识后,模型估计值与实际值吻合度高,液压系统效率特性整体上与排量比呈正相关。

3.3 对比与分析

为进一步验证I-MCM的先进性和有效性,笔者选择MCM和启发式优化算法,进行液压系统效率特性模型的参数辨识。

为确保3种算法对比的公平性,MCM和启发式优化算法的迭代运算次数相同,总计次数为30×10 000=300 000。由于6个待辨识参数的定义域未知,基于I-MCM的辨识结果,笔者将MCM和启发式优化算法的搜索区间统一设置为0～1 000 000。启发式优化算法采用一种改进的粒子群(improved particle swarm optimization,I-PSO)算法,详见文献[27]。

由于MCM和I-PSO算法同样具有随机性,因此笔者对每种方法各重复进行5次参数辨识试验,并进行对比分析。

3种方法的对比结果如表2所示。

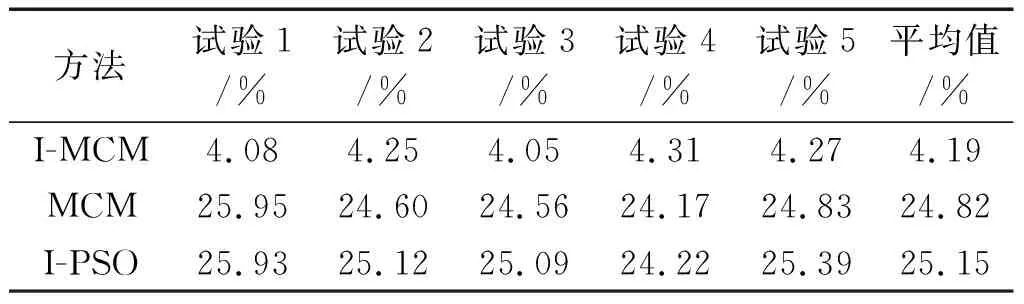
表2 3种方法目标函数值对比结果Table 2 Comparison results of objective function values for three methods

MCM和I-PSO算法的最优辨识结果如图6所示。

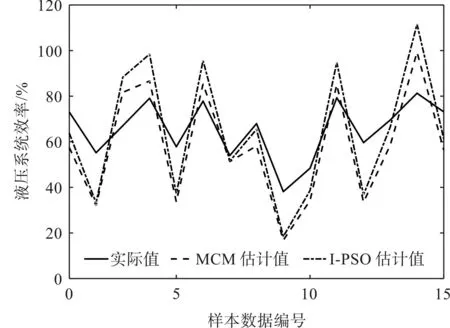
图6 MCM和I-PSO算法的最优辨识结果Fig.6 The optimal identification results of MCM and I-PSO

由表2和图6可知:在决策变量定义域未知的情况下,MCM和I-PSO算法的参数辨识效果差。

相较于笔者提出的I-MCM,前2个算法的绝对百分比误差均值分别增大492.36%和500.24%。

4 减速器传动比对整机能耗影响分析

由式(2)～式(6)可知:双级减速器传动比i0im影响了静液压传动系统中马达的输出端扭矩,并改变了整机行驶速度下对应的变量泵输入转速和变量泵排量比。因此,对于设计对象,其行驶速度在0 km/h～25 km/h范围内,且驱动轮负载扭矩变化时,整机传动系效率受减速器传动比设计值影响。

为进一步探究减速器传动比设计值对整机传动系能耗的影响关系,笔者采用单因素影响分析的方法,在双级减速器传动比最大值(19.66)范围内取5个水平(分别为8、10、12、14、16),利用前文所建立的效率特性模型,计算整机传动系效率。

整机传动系效率计算结果如图7所示。

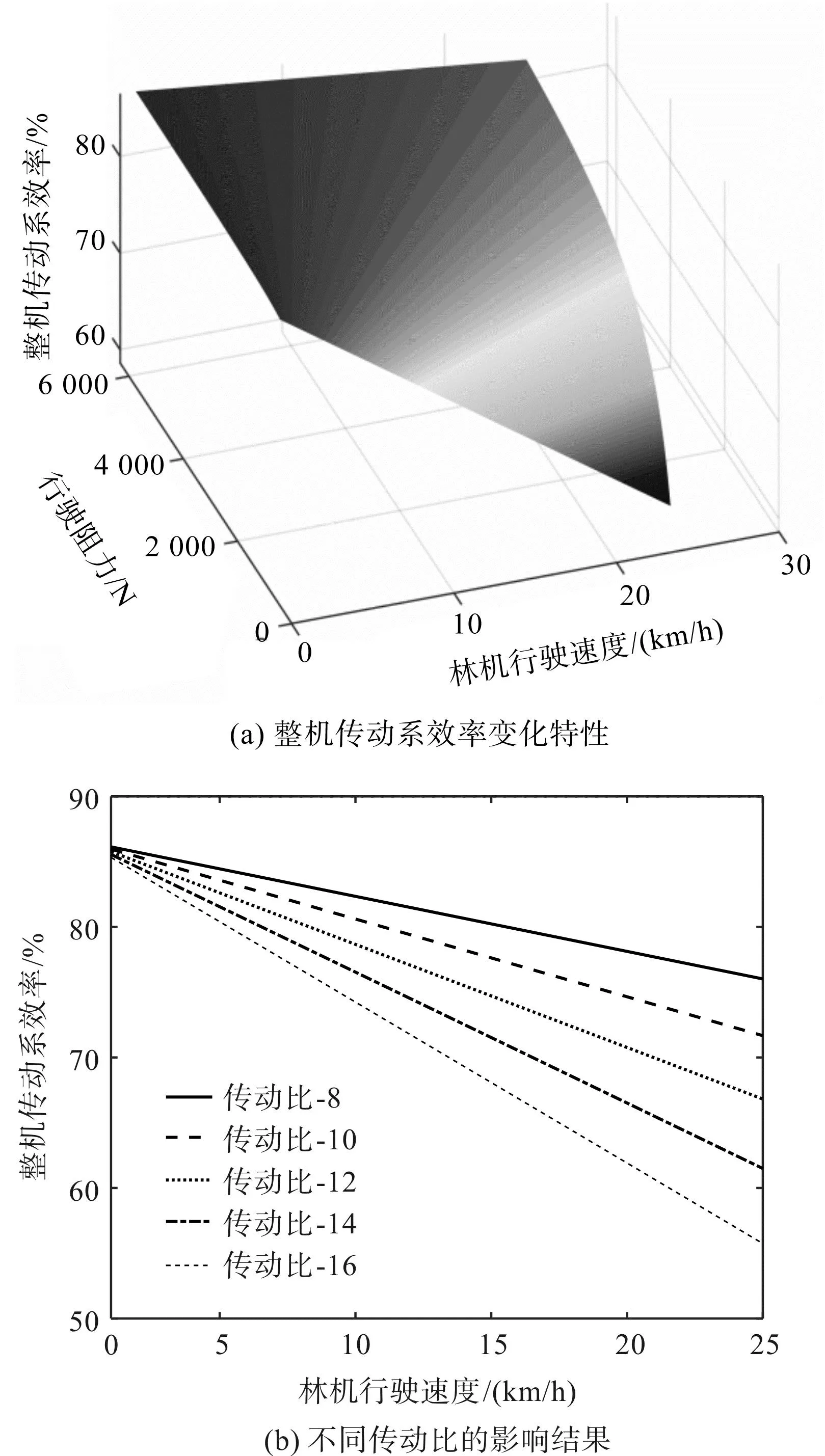
图7 整机传动系效率及影响因素分析Fig.7 Efficiency and influencing factors analysis of the whole machinery transmission system

图7(a)为双级减速器传动比为8时(示例),整机传动系效率变化特性;图7(b)为5种减速器传动比设计值下,整机传动系效率随行驶速度变化特性(同车速下,对所有负载转矩求传动系效率平均值)。

图7中,以双级减速器传动比i0im=8为例,中高行驶阻力下整机传动系效率较高;行驶阻力大于4 000 N时,整机传动系效率均值为83.66%;林机行驶速度对整机传动系效率影响较大,影响程度随行驶速度或减速器传动比值的增大而提升,1 km/h和25 km/h所对应的整机传动系效率均值分别为86.16%和76.73%,相差12.29%。

整机传动系效率与减速器传动比设计值呈反相关,全工况下整机传动系效率均值分别为81.45%(传动比为8)、79.20%(传动比为10)、76.69%(传动比为12)、73.92%(传动比为14)和70.92%(传动比为16)。

根据式(2)～式(6)、图5、图7可知:整机效率关于马达端负载转矩、变量泵转速和排量比呈非线性变化;并且传动比等差变化的同时,马达端负载转矩、变量泵转速和排量比的变化亦呈现非等差特点。这导致传动比等差增大时,整机传动系平均效率不均匀下降。

综上所述,相邻传动比的整机平均传动效率差值(传动比由小到大)分别为2.25%、2.51%、2.77%和3.00%。可见,随着传动比增大,整机传动系效率下降程度也略微增加。

5 结束语

笔者分析并推导了农林作业机械(特别针对停车作业的林果采摘机械)中搭载“变量泵-定量马达”的动力传动系统整机效率特性,计算了整机在松软土路面上行驶时的需求动力,并进行了液压系统选型;采用了I-MCM辨识了静液压传动系统效率特性模型的参数,并与MCM和I-PSO算法进行了对比验证,基于已建立的效率特性模型分析了减速器传动比设计值对整机能耗的影响情况。

研究结果表明:

1)整机双级减速器传动比为8,液压泵和液压马达分别选择林德液压HPV-02系列泵和HMV-02系列马达(最大排量为55 cm3/r),整机传动系平均工作效率为81.45%,最大工作效率为86.38%,最小工作效率为58.59%;

2)笔者提出的I-MCM,通过决策变量搜索范围自适应变化能有效解决待辨识参数定义域的未知问题,工程应用性良好。I-MCM能快速收敛至有效解,5次参数辨识重复性试验的误差均值为4.19%,平均迭代次数约为10。而MCM和I-PSO算法的参数辨识效果差,在搜索区域未知条件下基本难以获取参数辨识的有效解;

3)以集中式驱动与动力传动方案构建的农林作业机械液压式行走系统,其终端减速器传动比对整机传动系工作效率影响较大,不同取值下效率均值差异度最大达10.53%。减速器传动比设计值的合理减小有利于降低整机能耗。本例设计的整机在中低速下具有高工作效率特性,在高速下工作效率低,这与农林作业机械于松软土路面上行驶或作业时的特点(速度常低于12 km/h)相符。

后续的研究方向为:全方位增加静液压传动系统效率特性模型建模所用的样本数据量,例如引入不同排量的液压泵及液压马达的效率测量值,以期进一步验证I-MCM方法的有效性,并探究具有更高精度的液压系统效率特性计算表达式。