基于第一性原理GGA+U 方法研究Si 掺杂β-Ga2O3 电子结构和光电性质*

张英楠 张敏 张派 胡文博

(辽宁师范大学物理与电子技术学院,大连 116029)

1 引言

Ga2O3的禁带宽度为4.2—5.3 eV (不同晶体结构表现为不同的带隙),是一种直接宽带隙半导体材料,具有优良的化学和热稳定性,近期受到广泛关注[1].迄今已发现Ga2O3有5 种晶相结构:α-Ga2O3(刚玉结构);β-Ga2O3(单斜晶系);γ-Ga2O3(类尖晶石的亚稳态型);δ-Ga2O3(斜方晶系);ε-Ga2O3(六方或斜方).其中,单斜晶系的β-Ga2O3最稳定,其他相在一定条件下均可转换为β-Ga2O3[2].研究表明,β-Ga2O3具有适宜的禁带宽度、高紫外可见透过率、高击穿场强和介电常数、良好的化学性质和热稳定性,广泛应用于日盲紫外(UV)光电探测器[3,4]、深紫外透明导电电极[5,6]、高功率电子器件[7]、传感器[8]和显示阵列[1]等方面.

然而,本征β-Ga2O3的导电性往往较差,限制了其在光电领域的应用前景.因本征β-Ga2O3的价带最大值相对较低,导带最小值相对较高,杂质能级通常会变成深能级,所以选择合适的掺杂剂提高β-Ga2O3的光电性能具有重要意义[9].国内外研究者广泛研究了Si[10],Sn[11],Ge[12]和Cu[13]等多种元素的掺杂对β-Ga2O3结构和光电性能的影响[14,15].其中,Si 被认为是较合适的掺杂剂,一方面是因为Si 和Ga 的氧化物有相近的熔点,有利于调节适当的生长温度以获得高质量的Si 掺杂Ga2O3薄膜;另一方面,Si4+的离子半径(0.041 nm)接近Ga3+的离子半径(0.062 nm),可在尽量减小单元胞体积改变的前提下,Si4+取代Ga3+成为供体[16].最后,Si 掺杂后还会产生大量的自由电子,从而提高β-Ga2O3的电导率[17].

Varley 等[18]对β-Ga2O3中的施主能级进行了理论研究,认为Si 可作为浅施主实现有效的n 型掺杂,也可实现带隙可调.但也有一些学者通过实验发现,Si 掺杂未能实现对β-Ga2O3薄膜能带结构的调控和导电性能的提升.例如,Takakura等[19]发现利用射频磁控溅射方法生长的Si 掺杂β-Ga2O3薄膜的电导率并没有高于未掺杂薄膜的电导率,这与Varley 等[18]的理论预期结果不符.Gogova 等[20]用金属有机气相外延法(MOVPE)生长了Si 掺杂的β-Ga2O3薄膜,但霍尔和电导率测量表明,所得到Si 掺杂的β-Ga2O3薄膜是不导电的.针对Si 掺杂会给Ga2O3薄膜及其器件带来什么影响,目前还没有比较统一的看法,因此针对Si掺杂Ga2O3薄膜继续开展系统的研究非常有必要.

除实验研究外,最近国内外研究者对Si 掺杂β-Ga2O3薄膜也开展了一些相关的理论研究.Zhang 等[21]利用基于密度泛函理论(DFT)的广义梯度近似(GGA)方法计算了未掺杂和Si 掺杂β-Ga2O3的电子结构,并指出掺杂时Si 原子取代了Ga 原子,但计算出的β-Ga2O3带隙只有1.951 eV,明显低于4.9 eV[22]的实验结果.众所周知,带隙值的低估是标准DFT 计算的一个缺点,主要是由于缺乏对电子-电子相互作用的交换和相关势的精确考虑,但这可通过混合函数(HSE06)[23]和LDA/GGA+U[24]等方法来修正.Li 等[23]利用HSE06对未掺杂和Si 掺杂的β-Ga2O3电学和光学性质进行了计算,结果(4.3 eV)与GGA 方法计算的能带宽度(1.951 eV)相比有明显提高,但与实验结果(4.9 eV)仍有差异[22,25].Dong 等[26]采用GGA +U方法研究了氧空位对β-Ga2O3电子结构的影响,Ga 和O 离子的HubbardU参数分别为7.0 和8.5 eV,β-Ga2O3的带隙计算值为4.92 eV,与实验值一致,但Ga-3d 轨道的峰位于–14.8 eV 左右,与实验结果(–17.12 eV)[27]存在偏差,因此需要重新考虑HubbardU值.到目前为止,利用GGA +U方法对β-Ga2O3的电子结构和光学性质的研究还相对较少,特别是利用该方法开展不同Si 掺杂浓度对β-Ga2O3的电子结构和光电性质影响的探究更是少见.

基于此,本文采用基于密度泛函理论的GGA+U方法计算并讨论未掺杂和不同Si 掺杂浓度下(如无特殊说明,均指原子百分比) β-Ga2O3的电子结构和光电性质.首先,通过选择合理的HubbardU参数克服前人采用GGA[9,11,13]对Ga2O3进行理论计算时带隙总被严重低估或与实验结果不符的问题;其次,通过改变Si 掺杂浓度,探究不同Si 掺杂浓度对β-Ga2O3的电子结构和光电性质产生的影响,特别是通过对载流子迁移率和电导率的量化分析,讨论其导电性增强的物理机制,为下一步Si 掺杂β-Ga2O3实验研究和器件设计的创新及优化提供理论参考.

2 模型和方法

2.1 结构模型

β-Ga2O3具有单斜结构,空间群为c2/m,晶胞由(GaO6)八面体构成的双链沿b轴方向排列而成,链之间又以(GaO4)相连接.这种结构有利于自由电子的移动,为其用作光电导器件提供了基础[28].采用β-Ga2O3的1×2×2 超胞模型为例,Si 掺杂β-Ga2O3的取代掺杂模型如图1 所示,该模型具有两个非等效的Ga 原子,分别是与最近邻4 个O 原子键合形成的四面体Ga(1)以及与最近邻的6 个O 原子键合形成的八面体Ga(2).根据O 原子与Ga 原子的相对位置,O 原子具有3 个结晶学上不同的位置,分别表示为O(1),O(2)和O(3).O(1)是三价离子,连接了2 个四面体和1 个八面体;O(2)为四价离子,处于3 个八面体和1 个四面体交汇处;O(3)也是三价,位于2 个八面体和1 个四面体的交点.两个氧原子三角配位,一个四面体配位.因此,在进行取代掺杂时,需要考虑Si 原子取代Ga(1)原子和Si 原子取代Ga(2)原子的两种掺杂模型.

图1 Si 掺杂β-Ga2O3 的1×2×2 超胞模型,Ga(1)和Ga(2)分别表示四面体和八面体位置Fig.1.1×2×2 supercell model of Si-doped β-Ga2O3,where Ga(1) and Ga(2) represent tetrahedral and octahedral positions,respectively.

众所周知,形成能越低,掺杂体系越稳定,所以对Si 掺杂体系进行结构优化后,分别计算了它们的形成能.结果表明,取代Ga(1)原子的形成能(富Ga 为–2.142 eV;富O 为6.638 eV)低于取代Ga(2)原子的形成能(富Ga 为–1.494 eV;富O 为7.286 eV).因此,Si 原子倾向于取代Ga(1)原子来实现Si 掺杂β-Ga2O3.这与Zheng 等[29]和Dang 等[24]的分析结果一致.

综上,采用Si 原子取代Ga(1)配位进行掺杂,并构建了5 个单胞和超胞模型如图2 所示.图2(a)为未掺杂单胞模型Ga8O12;图2(b)是掺杂浓度为1.25%的超胞模型Ga31O48Si1(1×2×2);图2(c)是掺杂浓度为1.67%的超胞模型Ga23O36Si1(1×3×1);图2(d)是掺杂浓度为2.50%的超胞模型Ga15O24Si1(1×2×1);图2(e)是掺杂浓度为5.00%的单胞模型Ga7O12Si1.

图2 原胞和超胞模型 (a) Ga8O12;(b) Ga31O48Si1 (1×2×2);(c) Ga23O36Si1 (1×3×1);(d) Ga15O24Si1 (1×2×1);(e) Ga7O12Si1Fig.2.(a) Primitive cell and supercell models: (a) Ga8O12;(b) Ga31O48Si1 (1×2×2);(c) Ga23O36Si1 (1×3×1);(d) Ga15O24 Si1 (1×2×1);(e) Ga7O12Si1.

2.2 计算方法

在CASTEP 程序包中利用基于密度泛函理论的第一性原理平面波赝势方法计算未掺杂和Si 掺杂β-Ga2O3的能带结构、态密度、差分电荷密度和光电性质.在Perdew-Burke-Ernzerhof (PBE)中采用广义梯度近似(GGA)校正电子-电子相互作用和相关势.为了获得β-Ga2O3的精确能量带隙,引入HubbaardU方案来完善理论预测.采用GGA+U方法测定β-Ga2O3的能带宽度,UO-2p 和UGa-3d 参数分别为8.35 和14.0 eV[24,29,30].本文所有计算均在倒易K空间中进行,原子核用超软赝势描述,Brillouin 区的积分采用1×4×2 Monkhorst-Pack 特殊点对全Brillouin 区进行计算,计算时价电子组态为[Ga]3d104s24p1,[O]2s22p4,[Si]3s23p2.计算前采用LBFGS 算法对模型结构进行几何优化,其收敛标准: 单原子能量容差为1×10–5eV/atom、自洽场容差为1×10–6eV/atom、原子间最大受力为0.03 eV/Å,原子间内应力小于0.05 GPa,原子的最大位移为0.001 Å (1 Å=10–10m),平面波截断能量为450 eV.当优化精度满足上述所有参数时,即完成结构优化.

3 结果与讨论

3.1 结构分析

计算前β-Ga2O3的结构参数为a=12.23 Å,b=3.04 Å,c=5.8 Å,β=103.7°,通过GGA+U方法进行结构优化,计算后得到的结构参数列于表1,可知所得到的结构参数与理论结果和实验数据都非常接近[31,32].这说明本文所使用的计算方法和模型是合理的,可以使用上述参数探究β-Ga2O3的电子结构和光电性质.

表1 GGA+U 方法优化后未掺杂和Si 掺杂β-Ga2O3 的晶格参数Table 1.Lattice parameters of undoped and Si-doped β-Ga2O3 optimized using GGA+U method.

通过表1 可以发现,晶格常数b值和c值比掺杂前减小,这是由于Si 离子半径(0.041 nm)[33]比Ga(1)离子半径(0.047 nm)[24]小所致.此外,掺杂后Ga31O48Si1,Ga23O36Si1,Ga15O24Si1,Ga7O12Si1的体积常数大于未掺杂Ga8O12,并随着掺杂浓度的增加而逐渐增大,这主要是由于库仑斥力和Si,Ga 离子半径差异的共同作用导致.因为Si4+取代Ga3+会产生多余的自由电子,从而增强库仑斥力,进而增加超胞体积.虽然Si 离子半径小于Ga(1)离子半径,导致晶格常数b值和c值比掺杂前减小,但库仑斥力的作用比离子半径差的影响更大.因此,综合后的作用效果是Ga31O48Si1,Ga23O36Si1,Ga15O24Si1,Ga7O12Si1的体积常数大于未掺杂Ga8O12的体积常数.随着Si 掺杂浓度上升,部分晶格常数的变化并非呈现线性,这是因为我们选择了确定的Si 掺杂浓度(1.25%,1.67%,2.50%和5.00%),将模型沿不同方向扩胞导致的.因晶胞中a,b,c轴的长度不同,Si4+在不同晶格方向发挥的库仑斥力效果不同,导致部分晶格常数的变化呈现非线性,Li 等[23]采用第一性原理计算Ga2O3也出现了类似的现象.

为说明HubbaardU值对能带结构的影响,计算了GGA 和GGA+U方法下β-Ga2O3的能带结构和态密度(DOS),如图3 所示.布里渊区的高对称点位于G(0,0,0),B(0,0,0.5),C(0,0.5,0.5)和V(0,0,0.5),能级零点为费米面(水平虚线).由图3 可以看到,β-Ga2O3在G点既有导带最小值(CBM),又有价带最大值(VBM),说明β-Ga2O3是直接带隙半导体,这与实验结果一致[21].在图3(a)中可以看出,在GGA 近似下,β-Ga2O3的带隙仅为1.81 eV,与4.9 eV 的实验结果有明显偏差[22].此外,上价带宽仅为6.67 eV,与实验值(约7.37 eV)不一致[34].更重要的是,Ga-3d 态峰值位于VBM以下的12.61 eV 处,这与17.12 eV 的实验结果偏差很大[27].为了消除上述偏差,采用GGA+U法进行计算,校正后β-Ga2O3的带隙约为5.11 eV,与实验值[35]相符,如图3(b)所示.同时,上价带宽为7.78 eV,Ga-3d 态峰值为–7.11 eV,与实验结果–17.12 eV 吻合良好,因此用GGA+U法计算出的电子结构是合理的.除此之外,在图3(b)还可看到,CBM 和VBM 分别是来自Ga-4s 和O-2p 轨道电子的贡献,因此,β-Ga2O3的带隙是由Ga-4s 和O-2p 状态决定,这与其他计算结果相一致[36].

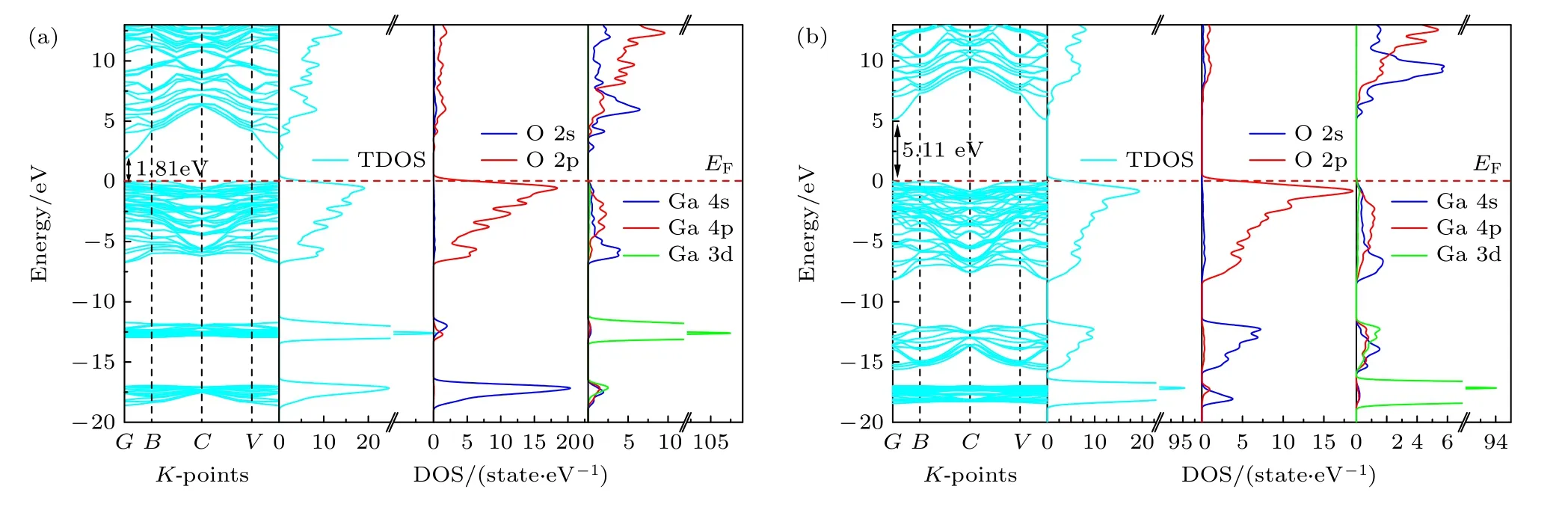
图3 β-Ga2O3 的能带结构和对应的态密度图谱 (a) GGA;(b) GGA+UFig.3.Band structure and corresponding density of states plots of β-Ga2O3: (a) GGA;(b) GGA+U.

3.2 掺杂形成能

形成能是预测掺杂体系稳定性和制备可能性的一个重要物理量.为了探究取代Si 掺杂β-Ga2O3的结构稳定性,根据(1)式计算掺杂体系形成能Ef[37]:

式中,E(GaOSi)为Si 掺杂β-Ga2O3体系的总能量;E(Ga2O3)为β-Ga2O3的总能量;μSi和μGa分别为Si原子和Ga 原子的化学势;化学势与材料的生长气氛有关,是影响Si 掺杂β-Ga2O3形成能的重要因素.因此考虑了O 气氛(富O)和非O 气氛(贫O),计算了Ga31O48Si1,Ga23O36Si1,Ga15O24Si1以 及Ga7O12Si1在富O 和贫O 条件下的形成能.在热平衡条件下E(Ga2O3)=2μGa+3/2µO2,贫O 条件下μGa=μGa(贫O),在富O 条件下μGa=μGa(贫O)+ΔHf[36].将计算得到的数据代入(1)式后,得到各掺杂系统的形成能如表1 所列.

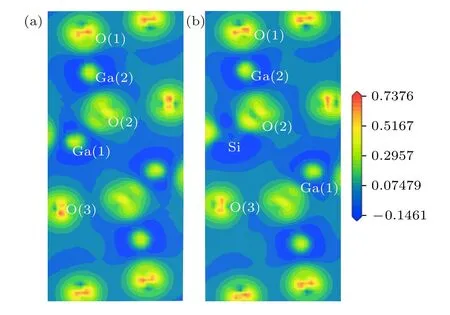
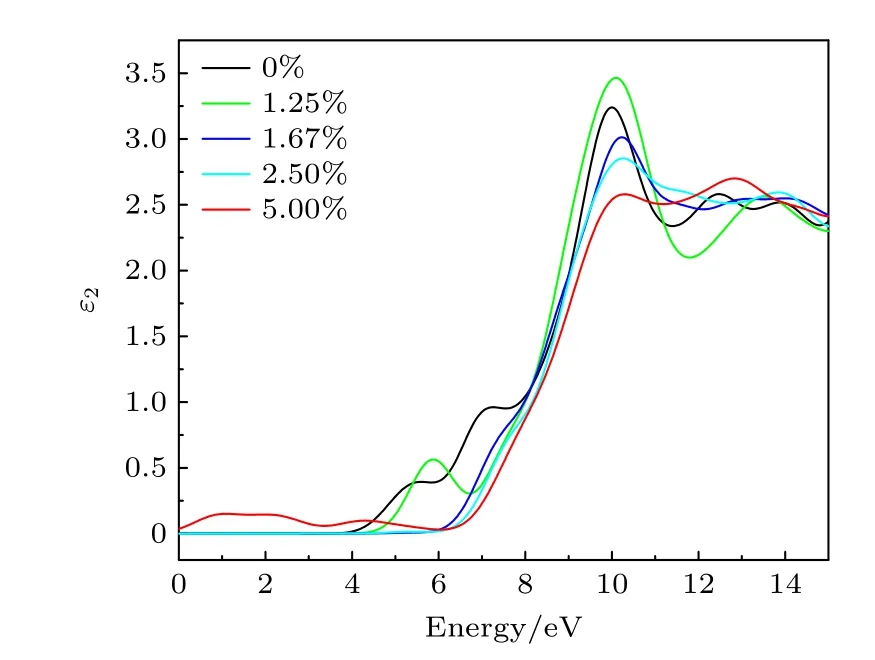
由表1 可知,贫O 条件下的形成能比富O 条件下的形成能低,因能量越低越稳定,说明Si 掺杂β-Ga2O3在贫O 条件下优先形成,且稳定性较高[29].在掺杂体系中,不同掺杂浓度对应的形成能大小顺序为Ga31O48Si1

3.3 能带结构

为了探究不同浓度Si 掺杂对β-Ga2O3电子结构和光电性能的影响,计算了Ga31O48Si1,Ga23O36Si1,Ga15O24Si1和Ga7O12Si1的能带结构,如图4 所示.可以看出,各掺杂浓度下β-Ga2O3的能带宽度在5.04—4.78 eV 之间,与实验值符合较好[16,38],这说明将β-Ga2O3中O-2p 和Ga-3d 的U值分别设为8.35 和14.00 eV 是合理的.由图4 还可以看出,β-Ga2O3导带底能级起伏较大,价带顶相对平滑,说明导带底的电子有效质量较小,而价带顶的空穴有效质量相对较大.在图4(a)—(d)中,Ga31O48Si1,Ga23O36Si1,Ga15O24Si1和Ga7O12Si1体系的能带宽度分别为5.04,5.00,4.94 和4.78 eV,由大到小依次为Ga31O48Si1>Ga23O36Si1>Ga15O24Si1>Ga7O12Si1,即1.25% >1.67% >2.50% >5.00%.与图3(b)中的未掺杂体系相比,Si 原子比Ga 原子能提供更多的价电子,且整个能带结构向低能方向移动,费米能级进入导带,显示出n 型掺杂特征.因此,Si 掺杂后的电导率显著提高,这与实验结果相一致[16,17,39].

图4 不同Si 掺杂浓度的能带结构图谱 (a) 1.25% (Ga31O48Si1);(b) 1.67% (Ga23O36Si1);(c) 2.50% (Ga15O24Si1);(d) 5.00% (Ga7O12Si1)Fig.4.Band structure plots of β-Ga2O3 with different Si doping concentrations: (a) 1.25% (Ga31O48Si1);(b) 1.67% (Ga23O36Si1);(c) 2.50% (Ga15O24Si1);(d) 5.00% (Ga7O12Si1).

图4 还显示出掺杂体系的能带宽度随着掺杂浓度的增加而减小.究其原因是,导带底和价带顶均向低能级移动,但导带底的减小幅度更大.因此,总体上导致能带宽度缩小[40].5.00%掺杂浓度相对于未掺杂和低掺杂浓度的能带结构,明显改变了其结构.重掺杂使导带和价带分裂出更多的带,进而影响了能带的结构,减小了能带宽度.但不同的Si 掺杂浓度并没有改变β-Ga2O3作为直接带隙半导体的性质.Si 掺杂β-Ga2O3的光学禁带Eg0(定义为价带顶(VBM)到费米能级的距离)大于β-Ga2O3的能带,随着掺杂浓度的增加光学带隙增大,这与后面Si 掺杂β-Ga2O3薄膜的吸收光谱一致.更大的光学带隙意味着Si 掺杂可以提高β-Ga2O3在深紫外光中的透光率,这对于紫外透明导电氧化物(TCO)材料的制备具有重要意义.

3.4 态密度

与能带结构对应的总态密度(TDOS)和分态密度(PDOS)也是很重要的数据,分析这些数据可以解释杂质的起源.不同Si 掺杂浓度0% (Ga8O12),1.67% (Ga23O36Si1),5.00% (Ga7O12Si1)和Si的TDOS 和PDOS,如图5 所示,随着Si 浓度的增加,态密度(DOS)逐渐向低能方向移动,费米能级进入导带,这与3.3 节的能带结构结果相符合.β-Ga2O3的价带主要由O-2p,Ga-4s 和Ga-4p 态组成,其中最大值被O-2p 态所占据.导带主要由Ga-4s,O-2p 和Ga-4p 态组成,其最小值被Ga-4s 态所占据.因此,β-Ga2O3的带隙是由O-2p 和Ga-4s 态所决定的.同时,能带结构中导带底比价带顶的减小幅度更大,说明Ga-4s 比O-2p 的作用效果更明显,这是由于Si 离子取代Ga 离子后自由电子增多所致.从图5(a)—(c)可以看出,未掺杂系统自旋向上和自旋向下的TDOS 是完全对称的,说明系统的总磁矩为0μB,是非磁性的.不同Si掺杂浓度Ga23O36Si1和Ga7O12Si1系统的自旋向上和自旋向下TDOS 也完全对称,表明掺杂体系也是非磁性的.相反,若系统的总磁矩不为0μB,则自旋向上和向下的TDOS 是不对称的,例如Yang 等[36]关于Nb 掺杂β-Ga2O3和Guo 等[41]关于Zn 和Cu 掺杂β-Ga2O3系统的总磁矩不为0(即自旋向上和向下的TDOS 是不对称).因此,无论掺杂与否,系统都不会显现磁性,不会对自旋电子产生影响.图5(d)显示了Si 的3s3p 轨道电子的PDOS 变化.由图5(d)可以看出,随着取代Si浓度的增加,费米能级进入导带增多,这表明更多的自由电子被掺入的Si 所吸引和诱导,并填充到CBM,进而改善β-Ga2O3的电导率.更重要的是,CBM 是被Si-3s 轨道电子所占据,说明Si-3s 轨道为改善β-Ga2O3的电导率做出了部分贡献.

图5 不同Si 掺杂浓度的DOS 图谱 (a) 0% (Ga8O12);(b) 1.67% (Ga23O36Si1);(c) 5.00% (Ga7O12Si1).(d) 不同Si 掺杂浓度的PDOS 图谱Fig.5.DOS for different Si doping concentrations: (a) 0% (Ga8O12);(b) 1.67% (Ga23O36Si1);(c) 5.00% (Ga7O12Si1).(d) PDOS for different Si doping concentrations.

3.5 差分电荷密度分布

通过分析差分电荷密度,可以进一步了解β-Ga2O3中原子间的电荷分布和成键情况[23,42].图6给出了未掺杂和Si 掺杂浓度为5.00%的β-Ga2O3的(010)面差分电荷密度分布.原子间电子密度的变化可以用来表示电子得失的程度,得电子区域用红色表示,失电子区域用蓝色表示;颜色条显示了–0.1461—0.7376 e/Å3的范围.可以观察到,在Ga原子和O 原子之间有显著的电子得失,这表明在Ga 原子和O 原子之间存在较强的静电相互作用.

图6 未掺杂(a)和Si 掺杂浓度为5.00% (b)的β-Ga2O3 010面差分电荷密度分布图Fig.6.Differential charge density distribution of undoped(a) and Si-doped β-Ga2O3 (010) surface with a doping atomic concentration of 5.00% (b).

掺杂前后,Ga2O3晶格中的原子间相互作用和体系中电荷分配均有不同.在图6(a)中,可以清楚地看到Ga 和O 之间的键合具有共价特性,其Ga原子失去电子,O 原子得到电子[43].由于Ga 原子和O 原子的负电性相差较大,大部分价电子被吸引到O 原子周围.图6(b)是Si 掺杂后的差分电荷密度分布情况,与未掺杂β-Ga2O3相比,Si 原子与其近邻O(2)和O(3)原子间共价性较Ga(1)原子强.当掺杂Si 原子替换Ga(1)原子后,负电性比Ga(1)原子强,所以与Ga(1)原子相比,Si 原子吸引电子的能力更接近O 原子,它们之间电子公有化程度加强.因此Si 掺杂能够提高β-Ga2O3的导电性.此外,与掺杂前相比,Si 近邻O 原子周围的电荷分布表现出各向异性,O(2)和O(3)原子的电子云中心偏向于Si 原子,而离 Si 原子较远的O原子电荷密度分布变化不大.

3.6 光学性质

通过计算分析介电函数ε(ω)=ε1(ω)+iε2(ω)和吸收光谱,可以评估材料的光学性质[41].介电函数: ε(ω)=ε1(ω)+iε2(ω)被分为实部ε1(ω)和虚部ε2(ω),实部与材料内储存的能量有关,虚部与能量损失或光吸收系数有关.ε2(ω),ε1(ω)和吸收系数可以表示为[44,45]

其中,M为偶极子矩阵,C 和V 分别表示初始态和最终态;k为波函数向量;ρ0为积分主值.

图7 给出了未掺杂和不同浓度Si 掺杂β-Ga2O3的介电函数虚部曲线图.可以看到,当Si 掺杂后,ε2(ω)主峰增强,但随着Si 掺杂浓度的增加,ε2(ω)主峰又逐渐减小.众所周知,ε2(ω)表征了材料对电磁辐射的吸收和能量损耗,当少量Si 掺入后,材料吸收电磁波的能力增强,可以激发更多导电电子.但随着掺杂浓度的增加,吸收能力下降,因此导电性受到抑制,这和实验结果一致[16].ε2(ω)的峰位可以用电子结构来解释,所有体系的主峰位于10 eV 左右,结合图5 的DOS 结果,分析认为这是由于价带O-2p 态向导带Ga-4s 态的带间跃迁引起的.此外,当Si 掺杂浓度达到5%时,发现在低能端有明显的吸收,可能是因为重掺杂导致带隙减小,在费米能级附近出现了Si-3s 轨道引起的杂质能级,进而价带O-2p 到杂质能级之间的跃迁产生了低能吸收,这和图5(d)的PDOS 结果相符合.还可以看到,Si 掺杂β-Ga2O3的吸收带边上升速度比未掺杂的要慢.结合图4 的结构分析,认为这是由于随着掺杂浓度的增加,光学带隙也逐渐增加,因此电子在进行跃迁时需要更多的能量,进而带边上升向高能方向移动,出现了蓝移现象.

图7 未掺杂和不同浓度Si 掺杂β-Ga2O3 的介电函数虚部Fig.7.Imaginary part of dielectric function of undoped and Si-doped β-Ga2O3 with different Si concentrations.

图8 绘制了Ga8O12,Ga31O48Si1,Ga23O36Si1,Ga15O24Si1,Ga7O12Si1的吸收系数与波长的关系,插图显示了300—790 nm 可见光区域的光吸收系数.由图8 可以看出,所有样品在波长小于260 nm的紫外范围内都有较大的光吸收,表明Si 掺杂β-Ga2O3具有较强的深紫外光探测能力.吸收强度的变化是由电子结构的改变引起的,由图8 得知,随着掺杂浓度的增加,吸收强度逐渐降低(红色虚线区域),带隙变窄,电子从价带顶向导带低跃迁所需的能量减少,而Si 掺杂后引入的杂质能级增多,因此价带与杂质能级之间和杂质能级与导带之间的吸收增强,导致带带吸收减弱.在可见光区域,其吸收光谱的强度随着掺杂浓度的增加而逐渐增加.可见光区域的光吸收是由于杂质能级与导带之间的跃迁引起的[30].当掺杂浓度较高时,吸收增强,因此可见光区域的光吸收随Si 的增加而增加,最高的掺杂浓度具有最好的光吸收性能,该结果为深紫外光电探测器件的设计和制备提供了一定的参考.

图8 未掺杂和不同浓度Si 掺杂β-Ga2O3 的吸收光谱,插图为局部区域(300—790 nm)吸收光谱放大图Fig.8.Absorption spectra of undoped and Si-doped β-Ga2O3 with different Si concentrations,illustrated as enlarged absorption spectra of a local region (300–790 nm).

3.7 迁移率和电导率分析

对于高掺杂浓度的掺杂半导体(如: >1019cm–3),影响其光学带隙的主要有两种相互竞争机制,分别是伯斯坦-莫斯效应[46,47]和带隙重正化效应[47].伯斯坦-莫斯效应由于费米带填充效应导致带隙扩大,记为∆EBM.带隙重正化效应由于多体带隙重正化效应和半导体-金属跃迁效应而导致带隙变窄,记为∆EBGN.∆EBM和∆EBGN可以表示为[48]

其中,Eg0为未掺杂的β-Ga2O3的能量带隙,为光学带隙,Eg为掺杂的能量带隙.

根据图3(b)和图4 中的能带结构示意图,Eg0=5.11 eV,随着Si 掺杂浓度的增加,Ga31O48Si1(1.25%),Ga23O36Si1(1.67%),Ga15O24Si1(2.50%)和Ga7O12Si1(5.00%)体系的Eg分别为5.04,5.00,4.94和4.78 eV.通过(5)式和(6)式,可得Si 掺杂浓度的∆EBM分别为1.02,1.12,1.43 和1.85 eV,∆EBGN分别为0.07,0.11,0.17 和0.33 eV.

式中,h是普朗克常数,ne是电子浓度.根据(7)式可以得到不同Si 掺杂浓度(1.25%,1.67%,2.50%和5.00%)的电子有效质量分别为0.3875me,0.3529me,0.2764me,0.2137me(me为电子质量).n 型半导体材料的电导率可以表示为[49]

其中,q为电子电荷,µ为电子迁移率,τ 是与电离浓度(Ni)和热力学温度有关的弛豫时间.由(8)式可知,电导率受电子浓度和迁移率的影响.因电子浓度和迁移率都随着掺杂体系增加,所以掺杂体系的电导率也逐渐增加[24].根据(8)式量化分析,Ga31O48Si1,Ga23O36Si1,Ga15O24Si1和Ga7O12Si1体系的电子迁移率分别为μ1/μ2≈0.910,μ2/μ3≈0.783和μ3/μ4≈ 0.772.结果表明,随着Si 掺杂浓度的增加,电子迁移率逐渐增加.

最后,Ga31O48Si1,Ga23O36Si1,Ga15O24Si1和Ga7O12Si1体系的电导率分别为σ1/σ2≈1.159,σ2/σ3≈0.582 和σ3/σ4≈0.687,因此随着Si 掺杂浓度的增加,电导率逐渐增大;并且电导率的增量是先增加后减小,与前面介电函数ε 函数数增的计算结果(激发导电电子的能力先增强后减弱)相符,这也与Hu 等[16]的实验结果和Liu 等[50]的计算结果一致.因此这一量化分析可以为Si 掺杂的实验探究提供理论参考.

4 结论

采用基于DFT 的GGA+U方法计算了Si 掺杂β-Ga2O3的形成能、能带结构、态密度、差分电荷密度和光电性质,分析了Si 掺杂对β-Ga2O3结构、能带结构和光电性质的影响规律,主要得到以下结论.

1) 当Ga-3d 态和O-2p 态的HubbardU参数分别设置为14 eV 和8.35 eV 时,β-Ga2O3的计算带隙、Ga-3d 态峰位和上价带宽与实验结果基本一致,可以改善GGA 方法计算电子结构的不合理性.

2) 在进行取代掺杂时,取代Ga(1)原子的形成能较低,说明该体系是稳定的,在实验中Si 原子可能优先取代Ga(1)原子;此外,在贫O 状态下体系的形成能更低,表明贫O 状态下制备的可行性更高.当Si 取代Ga(1)后,其近邻O(2)和O(3)原子间共价性增强,电子公有化程度加强,且Si 掺杂后总能带向低能端移动,费米能级进入导带和Si-3s 轨道电子占据CBM,从理论上解释了Si 掺杂β-Ga2O3提高导电性的原因.

3) 随着Si 掺杂浓度的增加,电导率逐渐增大,其增量是先增加后减小,与介电函数ε2(ω)的主峰强度先增加后减小相符,吸收带边上升速度比未掺杂的减慢.吸收光谱在260 nm 的紫外范围内有较大的光吸收,在可见光区域的强度随着掺杂浓度的增加而逐渐增加.