基于拓扑/二维量子材料的自旋电子器件*

江龙兴 李庆超 张旭 李京峰† 张静 陈祖信 曾敏 吴昊‡

1) (华南师范大学半导体科学与技术学院,广州 510631)

2) (松山湖材料实验室,东莞 523808)

3) (北京航空航天大学材料科学与工程学院,北京 100191)

1 引言

传统电子器件的发展长时间以来遵循摩尔定律,随着器件尺寸不断减小与集成度不断提高,无论是日常生活的改善还是科技技术的进步,都经历着从量变到质变的过程.然而近年来传统电子器件进一步降低器件尺寸的成本和难度大大增加,对信息处理能力的提高需要另辟蹊径.自旋电子学由此成为新的研究热点,自旋电子学器件利用电子自旋作为信息载体,可以使信息处理增加一个维度.此外它还有集成密度高、响应快等优势,并且能和传统电子器件兼容,充分利用电子器件的现有框架,因此成为了下一代信息器件最具潜力的发展方向之一.

自旋电子器件的核心功能是实现自旋的注入及自旋或磁性状态的调控和存储.目前自旋的电流注入是主流的研究重点,传统的自旋电流注入由强自旋-轨道耦合 (spin-orbit coupling,SOC) 材料,如重金属材料铂、钨、钽等,通过自旋霍尔效应或Rashba-Edelstein 效应实现.由于较短的平均自由程和散射时间,其电流-自旋转换效率比较有限(<0.1)[1–3],需要较大的电流密度来驱动磁矩翻转,因此器件的功耗比较高.另一方面,器件中各功能层,如SOC 层与负责自旋/磁状态存储的磁性材料层,面临界面的晶格失配产生的应力、缺陷、重构以及电子结构失配产生的高电子注入势垒等问题.解决这些问题是进一步提高自旋器件性能,走向实际应用的关键.新型量子材料,如拓扑材料、二维材料等,由于它们独特的量子特性与结构特征,为解决上述问题提供了潜在的新途径,成为自旋电子学的研究热点.

拓扑绝缘体 (topological insulators,TIs) 其体态呈绝缘体相,但同时拥有受时间反演对称性保护的导电表面态.该表面态由材料中强SOC 导致的价带和导带反转形成,其能带结构呈Dirac 线性散射关系.拓扑表面态能提供自旋-动量锁定,并且由于受时间反演对称性保护,表面态传输电子将不会受非磁性缺陷、杂质等散射中心影响,形成背散射.这些特性使得利用拓扑绝缘体作为SOC 层的自旋电子器件可以大大提高电荷-自旋转换效率,降低临界翻转电流密度.除此之外,拓扑半金属材料如Dirac 半金属、Weyl 半金属等,也能提供自旋-动量锁定的表面态,并且其电子有更高的迁移率,有望进一步提高自旋器件的能量效率.最近,反铁磁材料由于对太赫兹具有超快的动力学响应,以及不产生杂散场等特点,呈现出相较于铁磁材料的优势.反铁磁材料体系磁序的丰富性,结合拓扑材料拓扑序的多样性,能产生独特新奇的物理现象,从而给操控拓扑态、磁序提供了更多途径,并催生出了拓扑反铁磁自旋电子学的研究方向[4,5].目前大多数拓扑材料的拓扑性体现在其能带结构具有拓扑特征,而磁斯格明子则是一种自旋结构体现拓扑特征的准粒子拓扑j 结构[6,7],其拓扑特性同样使得它不易受散射中心影响,另一方面其对自旋力矩十分敏感,因此对其操控所需的功耗极低;与磁畴相比,它拥有更小的尺寸,可使存储密度大大提高.磁斯格明子的稳定借助于非共线Dzyaloshinskii-Moriya 相互作用,而该相互作用的前提之一是需要强SOC 作用,所以拓扑材料的强SOC特征在稳定及操控磁斯格明子方面也将发挥重要作用.

异质结器件的另一大问题来源于传统磁性材料与SOC 材料形成的低质量界面.二维材料表面不含悬挂键,靠范德瓦耳斯层间相互作用形成界面,不但避免了晶格失配带来的困难,还能形成原子级平整的高质量界面.目前已有研究人员利用hBN 材料作为中间势垒层,改善界面从而提高器件效率的报道[8–10].随着越来越多的二维磁性材料被发掘[11–16],用二维磁性材料代替传统磁性材料成为目前的另一研究热点.二维磁性材料不但能改善界面问题,其本身的磁性也表现出新奇特性,如磁性强度的层数调制,铁磁性和反铁磁性可随层数切换等[11,17,18].二维材料的低维性也使得磁性的调控,如通过场效应等,更加有效.除此之外,二维材料的独特结构与能带特征,使它拥有诸多优秀特质,如出色的电子传输特性、机械特性、化学稳定性等.同时二维材料是一个庞大的家族,可以提供物性的多样性.对自旋电子学而言,二维材料不但可以提供良好的自旋输运载体,如拥有较弱SOC的材料石墨烯等[19],还可以提供用以进行自旋操控的强SOC 材料如过渡金属硫族化物 (transition metal dichalcogenides,TMDs) 等[20,21].此外它的自旋特性可有效响应光、应力、电场、磁场等多种外部激励,实现基于自旋信号的传感器件.

二维材料层间为范德瓦尔斯相互作用,使得研究者们可以自由得堆叠不同二维材料形成异质结.前文讨论的拓扑材料,大多也都是范德瓦耳斯层状材料,例如Bi2Se3,Bi2Te3,Sb2Te3,Td-WTe2,PtSe2,PtTe2等.可以将二维磁性材料与拓扑材料堆叠在一起,制备成具有原子级平整界面的二维异质结器件,不但能大幅提高器件效率、大大降低器件的尺寸,更重要的是通过层间耦合、近邻效应等相互作用,有望在二维异质结器件中获取新的拓扑态、磁序,以及新的相互作用模式,从而激发功能实现的新逻辑.更进一步来讲,利用二维材料的多功能性,可以通过堆叠不同功能材料,实现集传感-运算-存储于一身的多功能集成器件,实现“全二维自旋电子器件”.

本综述将总结和讨论最近拓扑材料及二维材料在自旋电子器件研究中取得的进展.第2 节着重介绍拓扑材料/磁性异质结器件;第3 节讨论二维磁性材料与相关自旋电子器件的研究;第4 节主要总结目前全范德瓦耳斯层状材料组成的拓扑材料/二维磁性材料器件的发展.最后,将总结拓扑材料、二维材料在自旋电子器件应用中面临的主要挑战及未来展望.

2 拓扑/磁性异质结的自旋器件

近年来,拓扑绝缘体已经成为了自旋电子学的新兴材料[4,22–28].拓扑绝缘体的一个显著特征是其表面态电子的动量和自旋被锁定为相互垂直的方向.由外加电流引起的费米面平移可以在拓扑绝缘体的表面产生净自旋极化,如图1 所示.自旋积累扩散到相邻的磁性层,其自旋角动量可以在磁体上施加自旋轨道力矩[29,30],从而操控磁性材料的磁矩.除本征拓扑绝缘体以外,研究表明在具有手性边缘态的磁性拓扑绝缘体中,当存在类手性对称时,这种边缘态在边界处表现出拓扑稳定的自旋纹理[31].

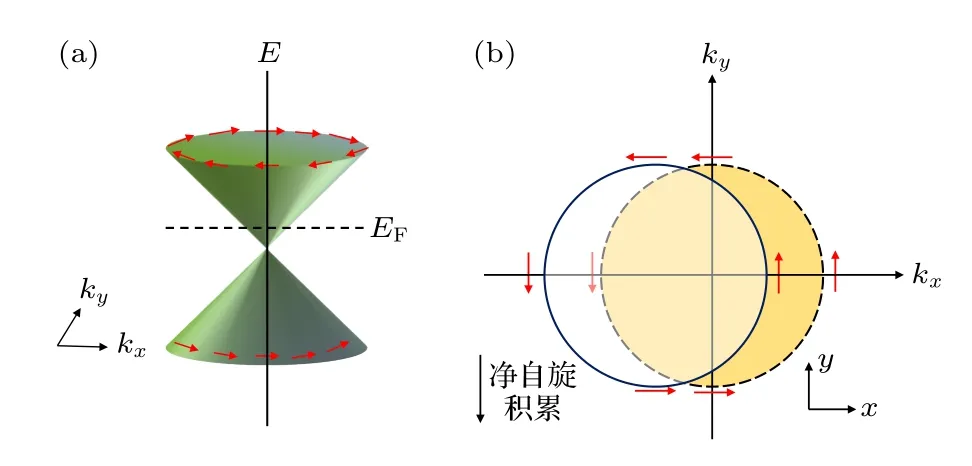
图1 (a) 拓扑绝缘体表面态中自旋动量锁定引起的螺旋自旋结构.箭头表示每个波矢k 中的自旋磁矩σ 方向,其方向与自旋角动量相反;(b) 沿+x方向施加电流,将在 电子的自旋和波矢处于正交方向的位置产生非平衡自旋积累[29,30]Fig.1.(a) Spiral spin structure caused by spin momentum locking in the surface state of topological insulator.Arrow indicates the direction of the spin magnetic moment σ of each wave vector k,which is opposite to the spin angular momentum;(b) applying current in the +x direction will generate non equilibrium spin accumulation at the position where the electron’s spin and wave vector are orthogonal[29,30].

传统SOC 层常用的自旋流材料是Pt,Ta,Hf,W[1,2,32–36].后来研究发现合金可以提高体系的自旋霍尔角 (spin Hall angle,SHA),比如AuW,AuPt,CuBi 等[37–43].除了单层金属和合金外,还可通过在重金属双层或多层的结构中使用插入层来修饰界面的方法实现对整体SHA 的提升.但是,由于重金属本身的自旋霍尔效应比较弱,受杂质散射的影响较大,因此SHA 的提高也遇到了很大的瓶颈.拓扑表面态由于自旋-动量锁定效应,且受时间反演保护,能有效抑制散射,单位电流可以对磁性材料产生的自旋轨道矩 (spin-orbit troque,SOT) 比重金属要大很多[44,45].基于拓扑绝缘体的SOT 效应在面内各向异性磁性金属 (包括NiFe 和CoFeB)的异质结中首先发现[46–48].后来,研究人员采用了具有体垂直磁各向异性 (perpendicular magnetic anisotropy,PMA)的铁磁和亚铁磁以及具有缓冲层的磁性多层作为磁性层,在具有PMA 的异质结中也观测了到高的SOT,并且临界翻转电流密度的量级为105—106A/cm2,与传统重金属体系相比,临界翻转电流密度降低了1 个量级[49–53].人们通过利用自旋矩-铁磁共振 (ST-FMR,S-F)、反常霍尔回线偏移 (loop shift,L-S) 和二次谐波测量(second harmonic,S-H) 等测量方法在各种拓扑绝缘体/磁性异质结中得到了体系SHA,但是SHA存在很大的差异 (0.1—425)[46,49–51,53–57],见表1.这些差异的基本物理原理仍然没有定论,通常归因于: 1) 拓扑绝缘体的高电阻可能会引起自旋电流分流效应;2) 拓扑绝缘体与磁性层界面处的能带杂化或者磁近邻效应;3) 拓扑绝缘体的质量,包括结晶度,表面缺陷,载流子浓度等;4) 测量温度以及界面自旋透明度等.

表1 不同异质结构的自旋霍尔角 (θSH),临界翻转电流密度 (Jc)Table 1.Spin Hall angles (θSH) and critical switching current density (Jc) of different heterostructures.

实验上得到的转换效率存在巨大差异,以及其不清晰的原理机制,也使人们对于拓扑表面态在提高电荷-自旋转换效率方面发挥的实质作用产生了一定的争议.研究人员通过调控费米能级位置,研究费米能级与拓扑表面态间相对关系对电荷-自选转换效率的影响.Fan 等[57]通过栅压调控费米能级位置,研究了磁性掺杂拓扑绝缘体的SOT,发现当费米能级在狄拉克点 (Dirac point,DP) 附近时能得到最大的净自旋电流/总电流比,且该比值与所测的SOT 有效场随栅压的调控呈一致的演化,如图2(a)所示.Wu 等[54]通过改变(Bi1–xSbx)2Te3中Sb 成分的浓度来调控费米面的位置,如图2(b)所示,发现当拓扑绝缘体的费米面接近DP 时,块体的绝缘性能和拓扑表面态的数量达到最大值的同时,系统拥有最强的SOT 有效场及翻转效率.Kondou 等[22]同样利用改变(Bi1–xSbx)2Te3中Sb成分的浓度来调控费米面的位置,利用ST-FMR研究了界面电荷-自旋转换效率与费米能级位置的关系.然而其结果表明,当EF穿过DP 时,在低温(10 K) 下SOT 效率显著降低,如图2(c)所示,并将其归因于DP 附近费米动量的不均匀以及螺旋自旋结构不稳定.拓扑表面态在提高电荷-自旋转换效率及SOT 效率方面的具体物理过程和物理机制还需要更深入的研究.

图2 (a) 通过栅压调控费米能级示意图,净自旋极化电流/总电流比 (左纵轴) 与SOT 有效场(右纵轴) 随栅压的演化[57];(b1) (Bi,Sb)2Te3中不同Sb 浓度的费米能级位置示意图;(b2) 二维载流子密度n2D 和电阻率ρxx,作为(Bi,Sb)2Te3 中Sb 浓度的函数;(b3) Jc 和SOT有效场与Sb 浓度的函数关系[54];(c) (Bi,Sb)2Te3 中不同Sb 浓度的费米能级位置示意图以及界面电荷-自旋转换效率与Sb 成分的函数关系[22]Fig.2.(a) Schematic view of Fermi level regulation by gate voltage and corresponding evolution of net spin polarization current/total current ratio (left longitudinal axis) and SOT effective field (right longitudinal axis) with gate voltage[57];(b1) Fermi energy level positions of different Sb concentrations in (Bi,Sb)2Te3;(b2) two-dimensional carrier density n2D and resistivity ρxx,as a function of Sb concentration in (Bi,Sb)2Te3;(b3) correlation between the effective fields of SOT and Jc and the concentration of Sb[54];(c) schematic diagram of Fermi energy level positions at different Sb concentrations in (Bi,Sb)2Te3,and correlation between interface charge spin conversion efficiency and Sb concentration[22].

此外,在具有磁性拓扑绝缘体(MTI)的系统中也有基于TIs 的SOT 的相关研究.Fan 等[58]设计制备出了拓扑绝缘体/磁性拓扑绝缘体[(Bi0.5Sb0.5)2Te3/(Cr0.08Bi0.54Sb0.38)2Te3]异质结,并在低于10 K 的工作温度下成功实现了SOT 驱动的磁化翻转,在极低温度1.9 K 下获得的临界翻转电流密度为8.9×104A/cm2,测得的SHA 高达425.随后,科研人员发现在MTI 系统中的非对称磁振子散射引起的电流非线性霍尔效应可能导致MTI体系的SHA 偏大 (临界翻转电流密度为2.5×106A/cm2,与基于重金属的系统相当)[59].此外,由于MTI 还保留了能带反转特征,因此拓扑表面状态也应该存在于MTI 的表面中,科研人员在GaAs/MTI/AlOx异质结中,采用加栅压的方法厘清了表面电子密度和SOT 效率之间的关系,揭示了拓扑表面态在TIs 基结构中SOT 产生的关键作用[55].

到目前为止,实验室中制备高质量TIs 基的异质结薄膜的方法多数为分子束外延 (molecular beam epitaxy,MBE),但是MBE 设备造价昂贵且不能大规模运用至工业化生产,同时TIs 的电阻率太大,不符合工业应用的节能要求.因此,科研人员考虑是否可以利用工业生产中成熟的磁控溅射技术(sputter)制备出高质量的拓扑绝缘体材料,随后Dc 等[52]率先使用磁控溅射技术沉积了BixSe1–x薄膜拓扑绝缘体材料并且获取巨大的SHA,此外该工作也实现了室温SOT 翻转.溅射多晶Bi2Se3也被证明可以产生大的θSH,同时实现较低的临界翻转电流密度[60–64].溅射薄膜方法可能是当前半导体制造中采用的实用方法之一.

3 二维磁性材料与相关自旋电子器件

自从石墨烯被发现以来[65],二维范德瓦耳斯(van der Waals,vdW) 材料家族不断壮大,迅速的扩展到各种具有奇异性质的材料,一系列新颖的物理现象不断被发现.但二维vdW 磁性材料在十多年间一直是该家族缺失的一员.直到2016年,二维反铁磁性才在单层FePS3中被发现[66].随后,Huang 等[11]于2017年发现单层CrI3和双层Cr2Ge2Te6被具有铁磁性.紧接着,Deng 等[67]证实另一种vdW 层状材料Fe3GeTe2中也存在二维本征铁磁性.并且他们还通过锂离子插层技术将少层Fe3GeTe2的居里温度 (Curie temperature,TC)提高至室温以上,打开了二维本征磁性材料的研究大门,也为自旋电子学的发展拓宽了道路.

二维vdW 磁性材料具有原子级平坦表面、表面无悬挂键等特点,且层间只存在范德瓦耳斯力,可以提供高质量界面,增加构建异质结的自由度,从而提高器件性能.其低维的特征可以大幅度降低自旋电子器件的尺寸,是实现全二维自旋电子器件的基石.此外二维磁性材料最大的优势在于它有更高效的磁性可调控性,如界面调控、磁电调控、应变调控等.这些调控方式一般通过改变二维材料或异质结的对称性、电荷分布、费米能级、价态、轨道占据、轨道杂化等性质实现.

二维磁性材料层间虽只存在范德瓦耳斯力,然而层间仍有可观的耦合相互作用,其磁性对不同的堆叠方式、层数、异质结构界面等较为敏感.如Cr I3中发现的随层数变化,材料在铁磁和反铁磁性间交替变化的现象[17,18].Fe3GeTe2的TC随层数不同而变化等[12].在转角CrI3中,还观测到了由摩尔超晶格提供的周期性堆叠顺序变化引起的铁磁与反铁磁织构交替出现[68].此外,在异质结构界面中也观测到了明显的二维磁性的界面耦合调控效果.Liu 等[69]发现Fe3GeTe2/CrSb 超晶格结构中,通过界面Cr 层自旋极化电子掺杂引起Fe3GeTe2的TC增强.Wu 等[70]构造了Fe3GeTe2/Cr2Ge2Te6异质结,通过异质结界面处的Dzyaloshinskii-Moriya 相互作用在界面两侧的磁性材料同时诱导出了不同的磁斯格明子结构,如图3(a)和图3(b)所示,其研究结果表明通过合理的设计多层二维vdw磁性材料堆叠,可以在垂直方向上形成不同的磁斯格明子结构,为基于磁斯格明子的自旋电子学器件设计提供了新的角度.

图3 (a) Cr2Ge2Te6 侧观测到的磁斯格明子;(b) Fe3GeTe2 侧观测到的磁斯格明子[70];(c) 双层CrI3 磁序的电切换,插图描述了不同磁场和电场作用下磁状态[71];(d) 三层Fe3GeTe2 中,以栅压和温度为函数的磁相图[67];(e) Fe3GeTe2 的透视图(石板蓝色和蓝色球分别代表Fe3+和Fe2+;虚线箭头表示铁原子间的自旋交换耦合)[74]Fig.3.(a) Skyrmion lattice observed on the Cr2Ge2Te6 side;(b) skyrmion lattice observed on the Fe3GeTe2 side[70];(c) electrical switching of the magnetic order in bilayer CrI3,and the insets depict the magnetic states under different magnetic and electric fields[71];(d) phase diagram of the trilayer Fe3GeTe2 sample as the gate voltage and temperature are varied[67];(e) perspective view of Fe3GeTe2 (The slate-blue and blue balls represent the Fe3+ and Fe2+;Dashed arrows indicate spin exchange coupling between Fe atoms)[74].

利用电场对二维材料中的磁性进行调控引起了许多人的关注和兴趣,因为电流不通过材料,从而不会产生热量和干扰在磁性非易失存储器中的写入.而二维材料比普通薄膜对电场更加敏感,因此在磁电调控方面具有巨大的潜力.Jiang 等[71]以反铁磁双层CrI3作为基态构建了场效应器件,通过在器件中施加栅极电压进行磁性调控并结合磁圆二色性显微镜检测磁性,证明外加电场可以产生层间电势差,从而实现线性磁电耦合,进而在恒定磁场下通过电场实现铁磁态和反铁磁态的相互转变(图3(c)).此外,二维磁体还能通过静电掺杂实现磁电调控.Wang 等[72]对Cr2Ge2Te6进行了静电掺杂,使Cr2Ge2Te6饱和磁化强度上升;Verzhbitskiy等[73]也进行了相同的工作,发现当电子掺杂浓度为4×1014cm–2时,TC从61 K 提高至200 K,且磁各向异性由面外变为面内.通过锂离子插层技术,Deng 等[67]研究发现高浓度的电子掺杂 (每层1014cm–2) 会导致Fe3GeTe2电子能带的偏移,费米能级上的电子态密度的大幅度变化导致铁磁性的明显调制,图3(d)为TC与栅压相关的磁相图,可以看出施加2 V 的栅压Vg时,TC从100 K 提升至300 K.

应变调控是一种简单而有效的磁性调控方式.应力可以改变二维磁性材料层间距和晶格结构,改变磁耦合方式,从而实现对磁性的调控.Wang 等[74]研究发现通过对Fe3GeTe2施加单向拉伸应力,可以改变该晶体的结构 (图3(e)),进而影响其磁晶各向异性能,当施加的应变为0.32%时,矫顽场显著增加,且随着应力的增大,Fe3GeTe2的TC呈线性增加.值得注意的是,实验还证实了对Fe3GeTe2施加的应变从0.65%提升至0.71%时可以实现磁化翻转.Chen 等[75]将单层CrI3和单层MoTe2组成异质结,将CrI3的TC提升至60 K,并通过施加4.2 GPa 的面外压力,减小了界面的层间距,引入了额外的自旋超交换 (Cr-Te-Cr) 路径,使TC可以进一步提高到85 K.

除了上述对磁性调控的研究,基于二维磁性材料的各种自旋电子器件的研究也引起了大量关注.Song 等[76]研究了使用CrI3薄片作为自旋过滤层的二维材料磁性隧道结,器件结构如图4(b)所示,Cr I3夹在少层石墨烯之间.图4(a)为双层CrI3磁性状态的示意图,左图为层状反铁磁态,其在零磁场下抑制隧穿电流,中间和右边两图分别为面外磁化和面内磁化的完全自旋极化态,不抑制隧穿电流.低温下,在具有4 层CrI3势垒的磁性隧道结中观测到高达19000%的磁电阻比,远高于传统自旋电子学器件.Lan 等[77]使用二维反铁磁体Cr SBr作为中间层构造了磁性隧道结,在5 K 下观测到了高达47000%的隧穿磁阻比,在130 K 也观测到50%的隧穿磁阻比.Wang 等[78]则构造了如图4(c)所示的Fe3GeTe2/h-BN/Fe3GeTe2异质结,通过反常霍尔测试观测到低温下160%的隧穿磁电阻.Albarakati 等[79]在Fe3GeTe2/graphite/Fe3GeTe2异质结中发现了罕见的反对称磁阻,相比于传统的巨磁阻器件只有两个阻态,此器件实现了高、中、低三个阻态.此外,TMDs 也常被用做异质结中间层.Zheng 等[80]构造了Fe3GeTe2/WSe2/Fe3GeTe2异质结,通过减小WSe2厚度实现了负磁阻 (–4.3%)到正磁阻 (+25.8%) 的变化;Lin 等[81]构造了Fe3GeTe2/MoSe2/Fe3GeTe2自旋阀器件,观察到3.1%的磁电阻,为传统铁磁电极自旋阀的8 倍;Zhu 等[82]构造了Fe3GaTe2/WSe2/Fe3GaTe2异质结,其磁电阻在10 K 时达到了164%,并且在室温下具有85%的磁电阻信号,首次在全二维范德瓦耳斯磁性隧道结中实现了巨大的室温隧穿磁电阻.除了各类磁异质结,基于二维磁性材料的SOT 器件的磁性调控研究也引起了广泛的兴趣.如图4(d)所示[83],在Fe3GeTe2/Pt 异质结构中,Pt 中x方向的电荷电流由于自旋霍尔效应产生z方向的自旋流,该自旋流在界面产生自旋积累,从而对Fe3GeTe2产生力矩作用.图4(e)为温度为100 K 时在50 mT 面内磁场辅助下实现电流驱动的磁化翻转,值得注意的是,SOT 操纵的两种霍尔电阻态不是完全饱和的,研究人员将其归因于热效应.电流驱动磁化翻转同样也能在绝缘二维铁磁体Cr2Ge2Te6中实现,例如Cr2Ge2Te6和Pt 或Ta 的双层器件[84,85],电流通过Pt 或Ta 产生自旋极化,在Cr2Ge2Te6/重金属界面产生自旋积累,使Cr2Ge2Te6磁化翻转.此外,通过电流感生SOT 产生磁化翻转的实验已在全vdW 异质结上实现,将在第4 节讨论.

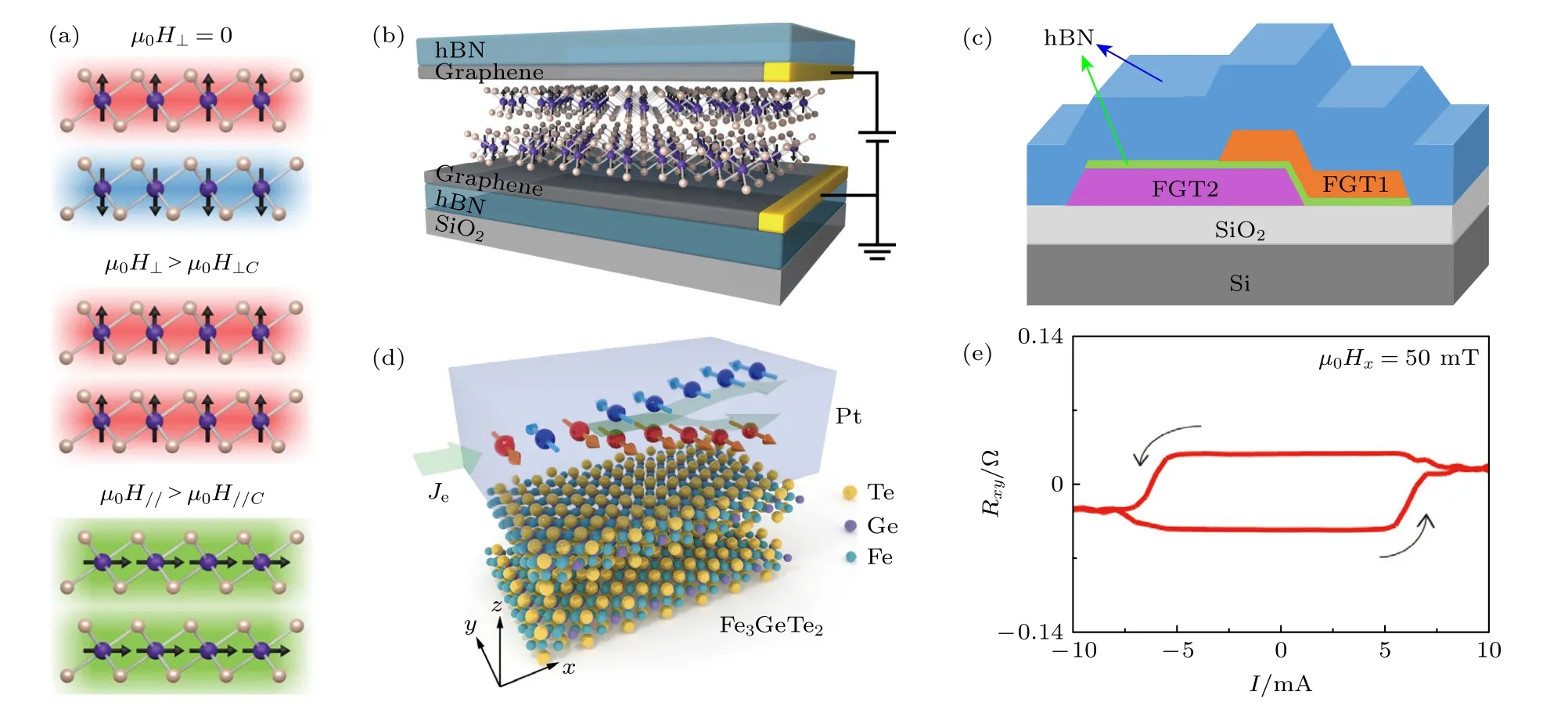
图4 (a) 双层CrI3 的磁状态示意图;(b) 二维自旋过滤磁性隧道结示意图[76];(c) Fe3GeTe2/hBN/Fe3GeTe2 的磁性隧道结示意图[78];(d) Fe3GeTe3/Pt 双层结构示意图;(e) Fe3GeTe2/Pt 双层器件中SOT 驱动的垂直磁化翻转[83]Fig.4.(a) Schematic view of magnetic states in bilayer CrI3;(b) schematic view of 2D spin-filter magnetic tunnel junction[76];(c) schematic view of magnetic tunnel junction for Fe3GeTe2/hBN/Fe3GeTe2[78];(d) schematic view of the bilayer structure for Fe3GeTe2/Pt;(e) SOT-driven perpendicular magnetization switching in the Fe3GeTe2/Pt bilayer device[83].

4 全范德瓦耳斯拓扑/磁性异质结和自旋器件

目前大多数热点拓扑材料均为vdW 材料,随着近年来越来越多高性能二维vdW 磁性材料的发现,全vd W 拓扑/磁性异质结和自旋器件成为了新的研究前沿.全vdW 材料间只存在范德瓦耳斯力,组装工艺不受限于晶格匹配或加工相容性[86],能充分发挥拓扑材料及二维磁性材料的潜力,进一步提高器件表现.此外vdW 拓扑材料及二维磁性材料拥有强烈层间耦合作用,使异质结展现出奇特的层间及界面调控现象;异质结具有原子级光滑界面能高效的发挥近邻效应[87,88].综上,全vdW 拓扑/磁性异质结不单单是对两者的简单功能组合,两者的相互作用或能激发新奇的物理现象,产生新的功能实现机制.

如前文所述,目前已有部分基于全vdW 材料的拓扑/磁性异质结和自旋器件被报道,如(Bi1–xSbx)2Te3/Fe3GeTe2[89]和Bi2Te3/Fe3GeTe2[90]等,它们的典型临界电流密度为106—107A⋅cm–2,与重金属/铁磁异质结构中的临界电流密度大小相当.其中,(Bi1–xSbx)2Te3/Fe3GeTe2双层器件的临界翻转电流密度随Sb 浓度的增加而增大 (图5(a)),而该双层器件的临界翻转电流密度在106A⋅cm–2量级 (图5(b)).Wang 等[90]利用MBE 技术制备出具有高界面质量的Bi2Te3/Fe3GeTe2异质结构,不但提高了FGT 的TC而且在低电流密度约为2.2×106A/cm2下实现了电流驱动的磁化翻转,其类阻尼SOT 效率高达约0.7.此外,传统的重金属/铁磁双层膜结构受限于对称性,通常产生的类阻尼力矩只能是面内方向,因此很难高效的驱动PMA 磁结构器件进行磁化翻转.通过构建低对称性的异质结构,利用对称性破缺能更有效的驱动二维PMA 磁性材料的SOT 磁化翻转.Shao 等[91]研究了 WTe2/Fe3GeTe2结构中电流驱动的磁化翻转,发现由 WTe2/Fe3GeTe2界面低导热而产生的焦耳热可以有效地调制Fe3GeTe2的矫顽力大小,在10 K 时,Fe3GeTe2的矫顽场大小随电流大小 (焦耳热) 的变化梯度 (ΔHc/ΔJFGT) 高达0.55 kOe⋅MA–1cm2.Shin 等[92]在全二维体系异质结构WTe2/Fe3GeTe2中实现了SOT 磁化翻转,利用电荷流经异质结的低对称面而产生面外的类阻尼力矩,在面内磁场的辅助下实现了对磁性层Fe3GeTe2的磁矩翻转;此外,在150 K 时该异质结的翻转电流密度显著降低,达到3.90×106A⋅cm–2,比传统的重金属/铁磁薄膜的翻转电流密度小了一个数量级 (图5(c)和图5(d)).Kao 等[93]通过实验证明,当施加强电流时,WTe2可以提供足够强的平面外抗阻尼SOT,进而在WTe2/Fe3GeTe2中实现热辅助的无外磁场的SOT 驱动磁性翻转,其中临界电流密度为1010A⋅m–2量级.这些结果表明,二维材料的低对称性能有效帮助产生面外抗阻尼力矩,为非传统SOT 驱动的高效磁化翻转提供了一条有前景的研究线路.

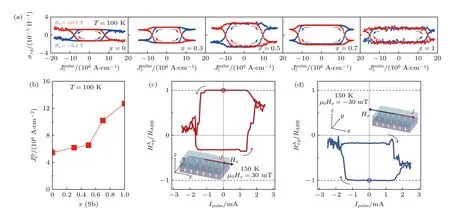
图5 (a) 不同 Sb 组分下的 SOT 驱动磁矩翻转的电流密度[89];(b) Sb 组分与 SOT 驱动磁矩翻转的电流密度依赖关系[89];(c),(d) 30 mT面内场辅助下的SOT 驱动的磁矩翻转[92]Fig.5.(a) Current density of SOT switching with different Sb component[89];(b) dependence of SOT switching current density on Sb composition[89];(c),(d) 30 mT in-plane field assisted SOT switching[92].

除了基于电学调控的二维自旋电子器件,超快太赫兹光自旋电子器件也是当前的研究热点之一.由于拓扑绝缘体具有自旋动量锁定的表面态,从而成为研究太赫兹自旋流的候选材料之一,也因此促进了二维vd W 异质结构的太赫兹光自旋电子学研究.Chen 等[94]研究了Fe3GeTe2/Bi2Te3异质结构中太赫兹自旋流的产生与控制,其数据如图6(a)—(c)所示,实验证明Fe3GeTe2增强了Bi2Te3辐射的太赫兹光谱强度.图6(d)显示,样品方向的翻转,会导致太赫兹光谱极性反转,进而证明是电偶极子而非异质结中的超快磁偶极子打破了空间反转对称性,引起自旋-电荷转换 (spin-to-charge conversion,SCC),从而辐射太赫兹波.

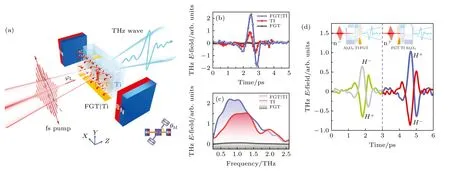
图6 (a) 飞秒激光脉冲激发和Fe3GeTe2/Bi2Te3 异质结构太赫兹辐射示意图[94];(b) 在太赫兹时域波形图中,Fe3GeTe2/Bi2Te3异质结构的太赫兹波明显增强[94];(c) 图6(b)的傅里叶变换图谱;(d) Fe3GeTe2/Bi2Te3 异质结构的太赫兹波极性翻转[94]Fig.6.(a) Femtosecond laser pulse excitation and terahertz radiation schematic diagram of Fe3GeTe2/Bi2Te3 heterostructure[94];(b) in typical THz temporal waveforms,the terahertz wave of the Fe3GeTe2/Bi2Te3 heterostructure is significantly enhanced[94];(c) Fourier transform spectrum of Fig.6(b);(d) terahertz polarity reversal of Fe3GeTe2/Bi2Te3 heterostructures[94].

全vd W 拓扑/磁性异质结和自旋器件除了上文介绍的具有自旋注入等功能外,异质结界面还具有丰富的相互作用,能实现高效的磁性调控和新奇的物性及现象.如Bi2Te3/Fe3GeTe2异质结中[95],Bi2Te3的拓扑表面态和Fe3GeTe2产生的界面耦合,增强了Fe3GeTe2的磁序,使Fe3GeTe2的TC由230 K 提升至400 K.此外,全vd W 异质结具有的原子级光滑的界面可以产生高效的近邻效应,如二维铁磁性材料可通过近邻效应,在二维非磁性拓扑材料中引入铁磁序等.Zhong 等[96]在全vd W异质结Cr I3/WSe2中实现了具有层分辨的磁近邻效应,实验上通过外磁场控制CrI3中单层的磁化状态,发现CrI3的界面主导了CrI3/WSe2之间的自旋相关电荷输运,而近邻交换场对整体层状磁结构高度敏感.Zhao 等[88]研究了全vdW 的反铁磁CrI3与量子自旋霍尔绝缘体 (quantum spin Hall insulators,QSHIs) WTe2螺旋边缘态的磁近邻耦合,在WTe2的边缘态中发现了对磁化状态敏感的非互易电流,非线性的边缘电导取决于最近邻层CrI3的磁化强度与电流的相对方向 (图7(a)),即通过改变CrI3的反铁磁状态,可以产生较大的非互易电流.Li 等[97]将铁磁绝缘体Cr2Ge2Te6与单层的WTe2组成异质结,通过磁近邻效应诱导WTe2产生铁磁性 (图7(b)),在这种磁化QSHIs中,明确地从局部输运探测中分离出了边缘和内部输运.此异质结边缘处非零的反常霍尔效应和反常能斯特效应响应 (图7(c)和图7(d)) 表明,磁化量子自旋霍尔绝缘体的边缘状态是部分自旋极化的,与量子反常霍尔绝缘体 (quantum anomalous Hall insulators,QAHIs) 的一维弹道手性边和QSHIs的螺旋边有质的区别.

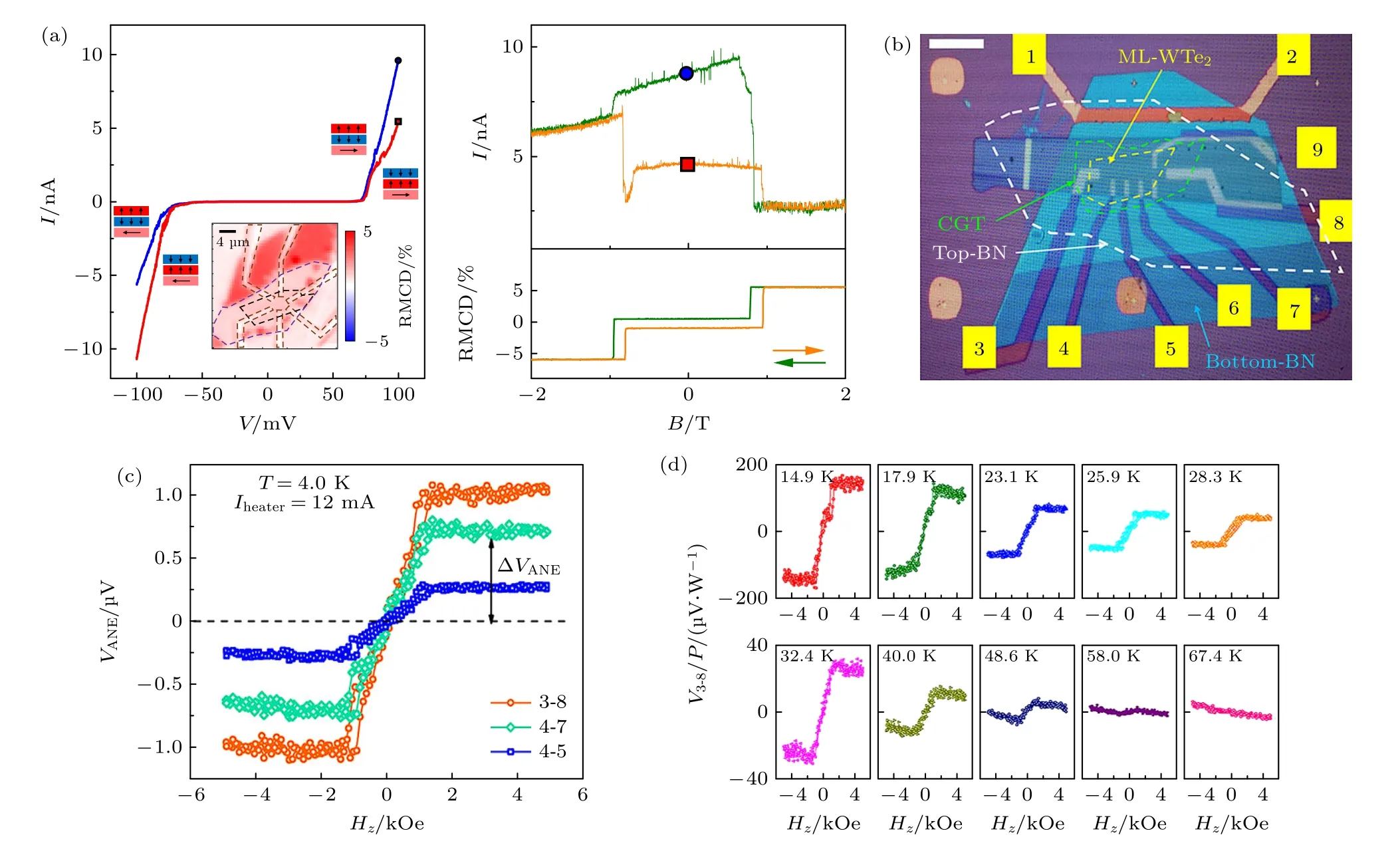
图7 (a) 反铁磁状态控制的大非互易电流[88];(b) ML-WTe2/CGT 异质结构器件的光学图像[97];(c) 不同测试通道的反常能斯特电压与磁场的依赖关系[97];(d) 归一化后的反常能斯特电压与温度的依赖关系[97]Fig.7.(a) Large nonreciprocal current controlled by the antiferromagnetic state[88];(b) optical image of the ML-WTe2/CGT heterostructure device[97];(c) dependence of abnormal Nernst voltage on magnetic field in different test channels[97];(d) dependence of normalized anomalous Nernst voltage on temperature[97].

5 总结和展望

本文系统回顾了拓扑材料、二维材料和全范德瓦耳斯异质结等量子材料体系在自旋电子器件中的研究和潜在应用价值.相比金属材料体系,量子材料体系具有独特优势,比如拓扑保护性、强自旋轨道耦合和比较长的自旋散射长度等.但是,面向未来大规模的自旋电子器件和芯片的工业级应用,还有一些关键性的科学和技术问题有待解决: 如何实现大尺寸的高质量拓扑/二维材料制备;如何将拓扑/二维材料与现有自旋电子器件相集成;拓扑/二维自旋器件在尺缩极限下 (<10 nm) 的性能;具有稳定性能和一致性的高密度阵列型拓扑/二维自旋器件和电路的设计和制备等.