知识建构社区中多主体模拟支持的观点涌现模型构建:复杂性科学的视角
2024-01-24胡金艳杨霞高兴启满其峰张义兵
胡金艳 杨霞 高兴启 满其峰 张义兵
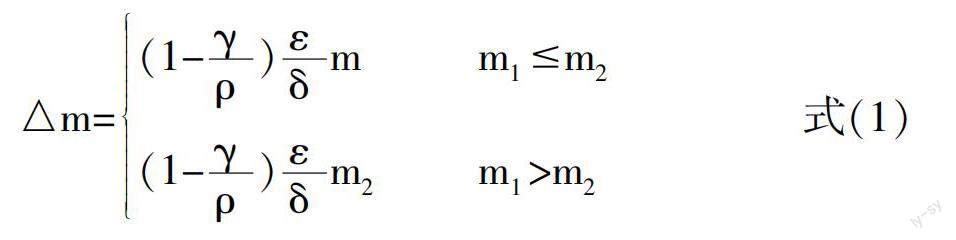



[摘 要] 以观点为中心的知识建构理论强调学习者像科学家一样探究真实问题,多个观点持续交互使得社区逐渐演变成一个复杂系统,非叠加态的观点呈现出不能被还原的涌现现象。然而目前对于观点涌现的研究止步于理念上对其系统属性的认识,仍然惯性地沿袭还原论的研究视角及范式,将复杂的涌现现象切割为单个观点甚至是片段化的关键词进行挖掘与分析,未能真正触及观点涌现的实质。基于此,本研究采用自下而上的多主体建模来探索观点涌现的规律和特征。研究发现,观点涌现层级越高需要的时间越长,难度也越大;高层级的观点会限制低层级观点的交互域;观点涌现过程中的能量值呈现从正态分布到指数分布的不均衡态势,从而为观点涌现研究提供了全新的视角和方法,对知识建构社区的教学实践具有多层次的解释力。
[关键词] 知识建构; 观点涌现; 多主体模拟; 复杂性科学
[中图分类号] G434 [文献标志码] A
[作者简介] 胡金艳(1981—),河南漯河人。讲师,博士,主要从事知识建构和涌现论研究。E-mail:hujinyan07@163.com。
一、引 言
法国哲学家、教育家埃德加·莫兰曾无比担忧地说:“致力于传播知识的教育对于什么是人类认识、它的机制、弱点、困难和可能导致错误和幻觉的倾向一无所知。”他呼吁未来教育要清醒地认识并拥抱“不确定性”,正视知识建构的复杂性。学界对该类问题的激烈讨论以及学校教育轰轰烈烈的改革从未停止,具体表现在三个方面:其一,从研究的视角和方向看,被誉为“21世纪的科学”的复杂性科学作为系统理论发展的第三波浪潮正日益从自然科学界向哲学、人文社会科学领域渗透,逐渐成为教育领域新的科学思维方向;其二,从对人类学习的认识看,人们早已觉悟到类似于“知识从教师的头脑传递到学生的头脑是一件完全没有问题的事情”这一刻板观念的浅薄与局限,新的知识创造隐喻逐渐得到学界认可,诸如“儿童像科学家一样主动建构自己的知识”的建构论深入人心,以“观点(Idea)为中心”的知识建构(Knowledge Building,KB)理论就是该隐喻下的典型代表;其三,从研究方法看,复杂系统中的个体经过多层次互动生成创造性整体的核心理念决定了研究思路需要从自上而下的还原分解到自下而上的生成创造转向,多主体模拟(Multi-agents Simulation)便是该转向中具有代表性的方法。因此,本研究立足于复杂系统,将KB中的观点视为有生命的主体,多个观点经由多层次互动,形成难以预测的、动态变化的复杂网络系统,观点会表现出非叠加的、不能被还原的属性和特征,即复杂性科学层面的涌现(Emergence)现象。研究引入涌现论中经典的、自下而上的多主体模拟法,在NetLogo软件中进行观点涌现的模型构建研究。
二、研究背景
(一)复杂性科学与涌现论代表着系统理论的最近浪潮
复杂性科学是系统科学发展的第三波浪潮,代表着科学演化的第三种历史形态,这意味着科学思维基本方向的转变。复杂系统首先被应用于自然科学领域,随后,许多有洞见的学者将其拓展到人文社会科学领域。早在1999年,莫兰就从宏观层面呼吁将教育的任务确定为“迎战不确定性”,应用复杂性科学来重构教育问题。美国国家科学基金会在本世纪初专门建立学习科学中心来深入研究“复杂现象和多维数据的呈现与表征”。Forsman等认为复杂性科学可以作为一个理论框架扩展物理教育研究。Michael等明确将教育作为复杂系统,强调复杂性科学在概念和方法上对教育的重大影响。《剑桥学习科学手册》(第2版)专门增加了一章复杂性科学的内容。李曙华等通过研究系统科学与圣塔菲网络课程的结构,探索了MOOCs与现实课堂结合的教学模式。田浩等研究了复杂性科学视域下的学习干预。这些研究展现了复杂性科学在多学科领域的蓬勃发展,教育领域亦成为其发展的重要阵地。
涌现是复杂性科学的一个中心概念,代表着相互作用后的复杂系统具有部分所没有的特质。Sawyer基于社会学理论的结构范式和交互范式,提出了第三种范式——涌现范式。莱斯利认为,在建构主义理论的发展中,阻止任何代理分化和整合的主要障碍是当代理论中缺乏涌現的观念,知识碎片的叠加不会产生涌现,知识是被建构成潜在的行为和互动的组织。然而在当前的学校教育中,知识在学科之间被分割、肢解、简化和模块化的弊端日益显露,学界更加关注多学科性、跨学科性、超学科性、横向延伸的、多维度的甚至跨国界和种族的知识。观点涌现的提出正是对这种改革模式的一个回应,在KB社区中的观点群通过不断聚集和交互,最终演化为不同于原始观点的特性,即观点的涌现性。
(二)知识建构理论与涌现论在理念上具有相通性
涌现范式是不满于一般系统科学运用非线性方程将集体的性质还原为个体行为的做法,认为其不能解决社会涌现和现实问题而提出的;而KB强调社区知识的生成与创造,其前一个阶段是人类学习的“参与隐喻”,这和涌现范式兴起之前的“交互范式”理念一致。这足以说明二者发展背景和理念有相通相融之处。有学者用群体认知的概念来表示从团队成员相互作用中产生群体层面共同的理解,从而生成团队新的见解。观点涌现成为集体KB的一个重要特点,是系统更高层次上的事件或结构,不能通过孤立地考虑其较低层次元素的特征来充分理解。KB是创生新的群体层面的、无法依据已有知识预测的产品的过程,对复杂系统进行深入的理论与实践研究将极大地有助于对涌现现象的理解。
KB是对社区有价值观点的生产和持续改进,它以提高社区所能实现的远大于个体贡献总和的可能性为手段,并且成为扩展文化努力的组成部分。此定义蕴含了丰富的复杂性科学和涌现思想,观点一旦被记录到平台中,这种人造物就具有了自主性和生命力,具有某种自我创造与演化的机能,也可以被他人阅读、评论、批判、提升、质疑等。Li 等基于复杂性理论的模型,将知识视为自组织过程的涌现,明确将知识创造看成涌现过程。Gourlay等结合了卡尔·波普尔的“世界3”概念,将知识视为一种外部的、类似对象的存在,这和KB所依据的哲学理念和方法论相似。观点作为“生命体”不断发展和进化这一观念在学习科学界逐渐得到认可,Krauskopf等甚至将观点看作“文化基因”(Meme)来研究KB交流中的观点改进过程。这些研究充分说明了研究者对KB中观点改进复杂性的认识,甚至有学者认为由观点生成的概念性人工制品本质上就是涌现。有学者构建了自组织视域下的在线深度协作KB活动组织框架及策略,Hong认为KB社区具有自组织网络的特征,而自组织是与涌现密切相关的一个概念。“集体认知责任”是KB12条原则中极其重要的一条,某些新的洞见只能通过集体才能产生,对集体层面的关注和强调KB与涌现论思想的相互呼应,也说明了二者理念上的相通。
(三)从还原到生成的研究方法转向
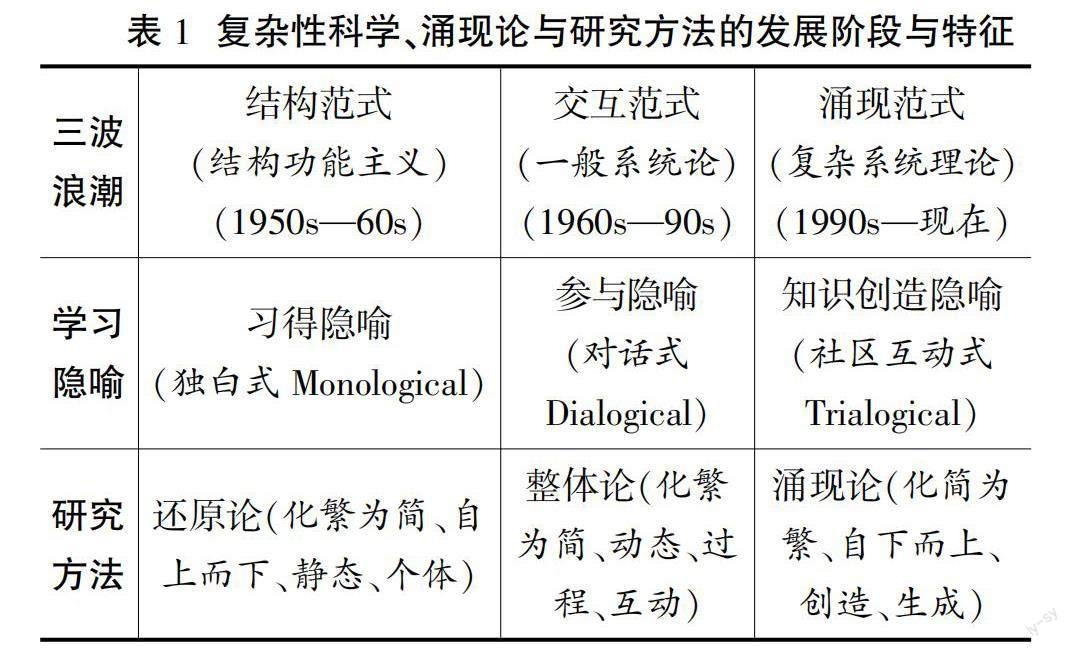
尽管有研究者关注到KB社区中观点改进的非线性、自组织、适应性等特征,但在方法上仍然停留在对观点的网络关系、阶段划分、轨迹跟踪等外在表现上,未能真正从非还原论视角对观点涌现现象进行解读。很明显,将研究视角定位到单个观点的还原论对这些现实问题的解决空间十分有限。实际上,观点在KB社区中有多个层次的涌现,完全解释其整体层面的特质需要突破还原论的极限。在研究方法层面,多数利用社会网络分析为研究学生互动密度的工具,挖掘成员在分享知识和推动探究方面的重要角色,但最终的分析单位仍然落在个体上。有学者将社区成员当作网络的节点,将成员间的联系当作节点之间的连线,对密度、中心性等网络指标进行分析,尽管聚焦到了系统的整体层面,但仅分析了表层化信息,并未对涌现作深入探究。计算机建模并未被广泛应用于KB观点改进的研究,与利用还原论的哲学视角相比,涌现论实现了从对单个观点到“观点群”的研究,不仅能够体现观点间错综复杂的关系,更能从整体视角对观点涌现的层次进行分析,正视知识创造过程中观点生成具有的复杂性。通过对复杂性科学、涌现论及相关研究方法的梳理,发现其发展现状和理念之间的关系可以用表1来表示。
综上,已有研究存在问题如下:其一,探索理念上虽对观点涌现现象有所认识,但止步于对其系统属性的认可,仍然惯性地沿袭还原论的哲学视角及研究范式;其二,研究方法上将复杂的观点及群体行为切割为单个观点甚至是片段化的关键词来分析,不仅难以洞察涌现出现的时机,更无法准确地把握KB浅层化的症结所在。因此,本研究将观点视为一个生命体,通过引入“熵”的概念将观点间的交互视为能量交易,采用计算机建模的方法来揭开观点涌现的“黑箱”。研究问题包括:非叠加态的观点是如何通过交互进行能量交易的,观点涌现的过程具有怎样的规律,观点涌现是如何实现层级跃迁的。
三、模型构建
根据研究问题进行观点涌现模型的设计和构建,具体包括多主体模拟介绍、模型构建思路、模型规则提炼三个部分。
(一)基于规则的多主体模拟
计算机模拟是认识复杂性和涌现现象的经典方法,现实中大量复杂现象都可以在模拟中得以重现。因此复杂性科学中存在着“非模拟不可推导” 的说法,模拟可以说是将复杂系统过程黑箱透明化的最佳手段和工具之一。多主体模拟是复杂系统范式中强大而严格的方法论,主张从多个主体出发,自下而上、基于规则地模拟与推理。具体来说,多主体模拟是将现实世界中纷繁复杂的现象和问题抽象为节点和连线的关系,并通过抽取规则來模拟涌现现象。本研究采用NetLogo来进行观点能量交易的模拟,该软件目前已经被广泛应用于生物学、物理、化学、社会学、心理学等领域中,是一个经典的复杂系统建模软件。研究者通过基于规则的多主体模拟系统向多个(几百甚至上千)主体(Agent)发出指令,通过计算机环境模拟多个主体自下而上、自然而然的涌现行为,直观地展现系统的生成、演化过程。
(二)观点涌现模型构建思路
观点之间的相互作用实质上是主体对物质、能量、信息等的传递与处理,观点接受其他观点的能量输入,同时可以输出能量。KB社区中观点的能量交易是双向同时发生的,即能量同时处于输入和输出的状态。该模型用来揭示观点在演化过程中能量变化导致的涌现现象,在经典“羊—草生态系统”和“人工经济”模型的基础上进行构建。前者是一个由羊和草构成的小型生态系统,核心规则包括:羊有一个能量值,吃草可以增加能量值;羊每个周期都消耗能量,能量值小于等于0会死亡;当能量聚积到一定水平时羊会繁殖,繁殖消耗能量,新出生的羊天然具备一定能量;草可以自发地从地里长出来的。人工经济模型的规则包括:一个经济系统中人和财富总量保持不变;初始状态每个人都有等量的货币;当两个人相遇时,财富发生随机转移。
为说明多观点交互而生成的涌现现象符合复杂系统规律,进而使用复杂系统的方法来模拟、证明乃至预测其走向,须引入“熵”的概念来进行推理。“熵(Entropy)”源自古希腊Trope一词,意为“变成”或“转化”,是对不能转化成功的能量的度量。通俗地说,熵代表一种无序度,在物质世界中,熵总是不断增加的,这是复杂开放系统的普遍规律,即“熵随时间增加”,KB社区中多观点间的交互系统自然也遵循此规律。从无序到有序是一个“熵减”过程,该规律最初用在自然科学领域,直到1929年匈牙利物理学家利奥·西拉德将熵与信息联系起来,从而奠定了信息论的基础和复杂系统的关键思想。之后数学家香农在继承玻尔兹曼思想的基础上开创了信息论这个新领域,明确用“熵”来定义信息量,即“香农熵”。至此用“熵”来解释观点能量交易便有了理论依据。观点通过交互获取有价值的能量(负熵),同时释放能量。从建构主义的视角来看,由不同的人所产生的观点(即便是针对同一个主题的看法)完全相同的几率是非常低的,因此,在交互中总会互相影响,不仅可以增加看待问题的角度,还可以刺激与驱动观点自身的聚集与生长。即使是两个完全相同的观点,在互动的过程中也可以相互印证,通过互相阅读形成该观点的证据和理由,增强彼此的信心,为其更深入的发展奠定基础。
(三)模型演化规则的提炼
1. 模型规则提炼
从复杂性科学的角度来看,KB社区是一个开放自组织系统,观点由于“熵增”而不可避免地走向无序,要想变得有序则必须通过有效交互来吸取“负熵”,否则当能量被耗散殆尽观点就会死亡。即没有任何交互的观点会成为一个封闭系统持续产生熵增。从这个角度看,观点涌现是“产生于无序之中的有序”。依据熵增定律,观点每个周期都会消耗能量,如同生物体的新陈代谢一样,能量交易实质上是观点能量值的积聚或耗散,因此,观点对负熵的吸收也代表了其在系统中的适应度。观点具有一个初始能量值100(不对观点的深度作价值判断,聚焦于观点的持续改进)。如同人工经济模型中货币转移规则一样,将每个观点视为拥有一定能量值的分子,观点交互可以增加一个随机的能量值。这也是“对等的知识发展”之原则所决定的,即两个交互的观点能量值都增加一个随机数。相反地,观点每一个周期都在消耗能量,熵增会导致观点逐渐沉寂、萎缩直至死亡或消失。死亡的观点如果得到其他观点的主动交互,会重新获取能量,当获取的能量达到一定阈值,就会复活。能量值累积到一定水平观点就会繁殖,将这种繁殖视为一种涌现,繁殖行为会消耗观点的能量。
假如一个观点总是与同一个观点进行交互,那么它们能够转移的能量会越来越少,因为这两个观点会逐渐趋同,形成捆绑、封闭、保守发展的态势,在系统中的开放度降低而持续地产生熵增。多个领域的学者都得出过类似的结论,如有学者研究了近年来241个学科的数以亿计的同质化科研论文,得出这类论文的暴增会从根本上严重阻碍科研进步和创新思想出现的结论,新团队在科学研究的多个方面都比固定旧团队具有优势。综上,最终提炼出的规则如下:观点群构成了一个生态系统,观点每个周期都消耗能量;初代观点一经发表,都具有等量的能量值,发生交互则随机增加该值;不同代际的观点具有不同的交互机会,其所传递的能量值就低不就高;当能量积累到一定水平,观点会繁殖(繁殖消耗能量),新出生的观点具有一定的能量并具有更高的交互能力和繁殖能量;假如一个观点与同一个观点交互多次,其传递的能量会越来越少;死亡的观点得到交互机会能够获得能量,当能量积累到一定水平则可以复活。
2. 模拟实现思路
当两个观点相遇时,可以用m来表示观点主体1的能量值,用m来表示观点主体2的能量值,它们相互作用时会发生能量的转移和变化,借鉴“人工经济”模型中的财富转移公式,引入跨层级交互系数,两个观点主体能量交易(含跨层级)的公式为:
△m=(1-)m m⩽m(1-)mm>m 式(1)
其中△m是观点交易的能量值,ρ是总层级数,γ为参与交易的两个观点间的层级差,每层观点交易的能量值是不同的。ε是观点每次参与交易的能量值,δ是同组观点交互的频数。
当每个层级的观点能量累积到一定的程度会进行繁殖,繁殖的能量临界值(h)的公式为:
=m+∑φm 式(2)
其中,m为父级观点能量的初始值,n为代际值,φ是代际之间的差值比。能量交换为观点涌现创造了条件,能量的交换与转移可以生成新的模式,观点选择性地交换能量使自己更好地生存,观点通过能量的积聚和耗散而产生的繁殖行为是更高层级的涌现。
四、模拟过程与结果
根据观点能量转移的规则,在NetLogo模拟界面中设置观点的可调节规模,周期性投放新观点。每个层级的观点能量初始值递增,观点消耗和转移的能量均设置为可调节的滑块。观点低于一定的能量值会停止运动,达到初始值后又重新开始运动(复活)。在绘图框中显示和分析总能量值的变化曲线、各层级的能量值变化和观点个数变化曲线、停止交互的观点个数曲线以及观点能量值分布直方图,如图1所示。
(一)观点涌现层级越高,需要的时间越长,涌现难度也越大
与人工经济模型不同的是,系统中的观点数和总能量值并非恒定,而是会随时间和观点交互而变化。由图2左下可知,总能量呈上升趋势,结合图2左上各层级的能量动态变化情况,发现各层级的变化情况有较大差距。由图2左上可知,初代观点产生后,经过短暂交互约在20 ticks之后就有下一代观点被繁殖,二代观点能量增长迅速,在短时间内总能量值超越其父代并在150 ticks之后繁殖出三代观点。三代观点的能量聚集起初较为缓慢,其父代观点能量下降时说明有较多观点被繁殖,三代观点能量迅速上升。结合图2右上的个数变化,尽管初代观点的个数持续增加,但由于更高层级的观点占据了主流,其交互机会减少,能量值并未持续上升。在运行了800 ticks之后才有四代观点出现,且能量增长极其缓慢。这表明了初代观点较容易与其他观点传递能量并涌现出下一代观点,但形成稳定的高级涌现则需要经过长时间坚持不懈的能量聚集。即层级越高观点涌现的难度越大,需要的时间也越长。一个层级观点能量值从升高到逐渐平稳或降低代表繁殖后观点能量值回落,也意味着更高一级的观点即将增加。模型中运行的步数不仅表示观点交互的时间,还代表能量的流转量,即必須经过一段时间的能量积聚,才会有涌现现象发生。
(二)高层级的观点涌现会限制低层级观点的交互域甚至导致其发展停滞
每个观点通过规则感知局部信息,在模拟环境中与其他观点进行非线性的相互作用。观点停止运动代表该观点交互域减小,交互机会降低。依据理查德·道金斯的Meme理论,一个观点从产生之初便具有延续下去的基因,而且总是趋向于和能够增加自己能量值的观点靠近,和与自身相关的观点(相似或相反)具有天然的吸引力,进而催生涌现现象的发生。从图2右下停止运动的曲线看,初代观点停止运动的最多,其次是三代观点。这是因为初代观点虽然每个周期都有相应的增加,但随着更高层级的观点出现,初代观点的交互机会降低,尽管数量不断上升,其能量值却很难持续增加,较多的观点由于缺乏交互机会导致能量值低于100而停止运动。这种停止运动的状态代表了观点在较长时期内是孤立的,很少甚至完全没有机会和其他观点进行交互,未能吸取负熵,而能量却在周期性地损耗。三代观点比二代观点停止运动的更多,也是因为交互域的影响,当二代观点聚集能量并逐渐占据主流时,虽然有三代观点的出现,但其数量有限,与低层级的观点交互机会受限导致有较多的观点停止运动,需要积累一段时间的能量之后才能逐渐发展。
(三)观点能量分布呈现从正态分布到层级跃迁之后指数分布的变化规律
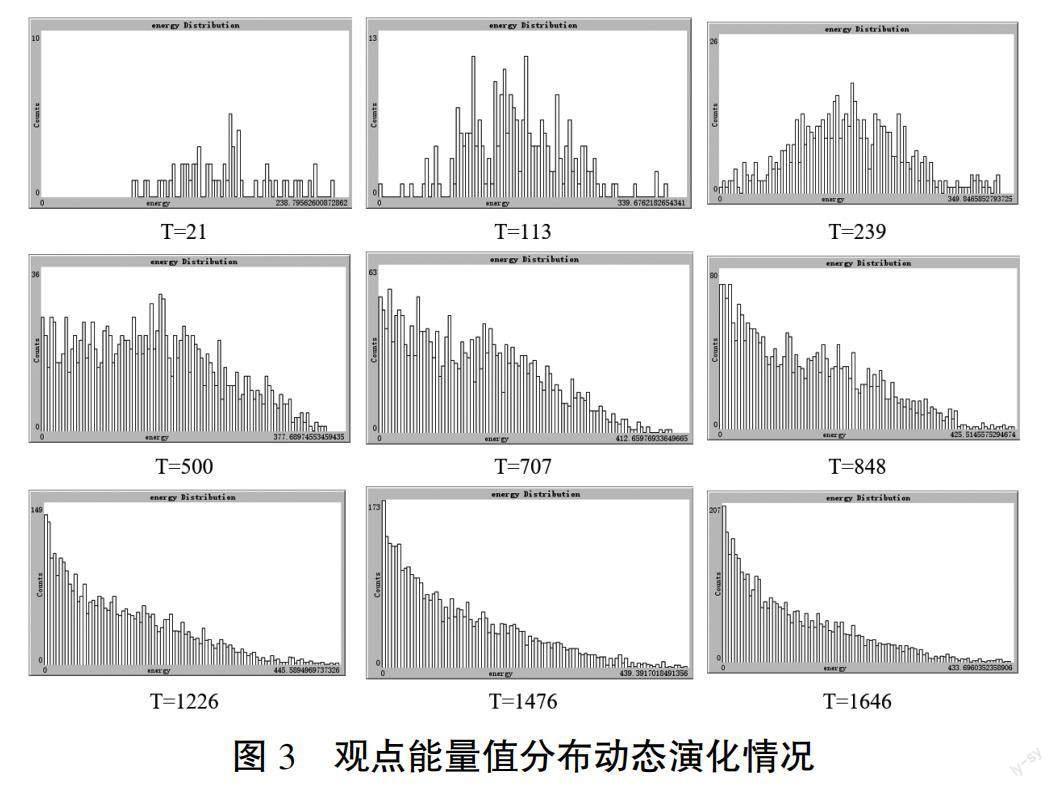
为分析观点能量分布动态变化情况是否均衡,本研究使用NetLogo的绘图功能来显示不同时刻观点能量分布状况直方图,如图3所示,横轴代表观点能量区间,纵轴表示该区间的观点数量。可以看出,不同的时刻观点能量值分布有较大差异,初代观点的能量值较低,经过百步的交互之后,能量值迅速上升并呈现完全不同的分布状态,在千步之后逐渐趋向稳定。
为进一步了解观点能量变化的趋势,利用Matlab 的分布直方图绘制工具Dfittool和分布拟合工具DistributionFitter对上述数据进行拟合。从整体上看,当初始观点开始交互时,其能量值分布较平均和集中,随着观点持续相互作用,其能量值呈现出正态分布,如=113、239时刻。对=239时刻的能量值进行拟合,发现其峰度值为-0.817,偏度值為0.562,服从正态分布。随着观点的深度互动和高层级观点的不断涌现,观点总能量值增高,低能量值的观点数量增多(如=500 ticks之后)。对=1226时刻的分布情况进行分布拟合,拟合优度R-square值为0.9323,均方根误差为7.9580,说明服从指数分布,即该时刻随着观点能量(x)的减小,观点个数(y)呈现指数级的增加。且当系统继续运行,如=1476、1646 ticks时直方图并无大的改变,收敛在指数分布,其发展逐渐呈现不均衡的态势。这和一般的复杂系统能量分布类似,如经济、社会、生态等系统中能量的积存和释放一般也具有这样的指数规律,也即系统中的观点能量值分布朝着不平等的趋势演化。
五、结论与讨论
(一)观点涌现模型对现实KB社区具有多方面的解释力和启示
第一,观点持续而充分的交互是其涌现的前提,未经深度交互的观点会不断消耗能量而逐渐处于停滞状态,很难达到高层级的观点涌现。KB教学中无论小组的形成还是突破性进展的取得都不是线性的,可能需要经过长时间的能量聚集才会发生,因此,师生都需要认识到过程的不确定性,在持续推进中有足够的耐心。第二,尽管不同层级的观点可以共存,但高层级观点占据系统中的主流地位时,会限制低层级观点的发展,因为观点总是倾向于和能提供更多负熵的观点交互。这说明虽然观点交互活动的边界是模糊的,但一个观点并不是漫无边际地和所有观点具有同等的交互机会,一个层次相差较多的观点也较难融入群体中,这说明观点要想得到好的发展,必须拥有足够多的交互机会,使自己成为“入群者”,避免被孤立而导致发展停滞。第三,观点能量值分布的直方图从正态分布收敛到指数分布表明能量分布的不均衡。这说明并不是每一个观点都能得到同样的发展,有些观点通过能量交易聚集在一起生成有前景的研究主题,有些观点融入某个群体中,而一些琐碎的、探究空间较小的观点会逐渐停止发展,这说明并不是每个初始观点都能够有较高级别的涌现。当学生外化和清晰表达他们发展中的知识时,他们学得更有效。学生不是先学习一些东西然后再把它表达出来;相反,最好的学习是当学生清晰地表达他们尚未形成、仍在发展中的理解,并在整个学习过程中不断清晰地表达。在KB的理念中,教育者也不是将知识加工成熟之后才教给学生,而是学生从各种不成熟甚至幼稚的、错误的观点中逐渐涌现出对于他来说全新的创造性知识。
(二)观点涌现是观点能量积聚中一次次的层级跃迁
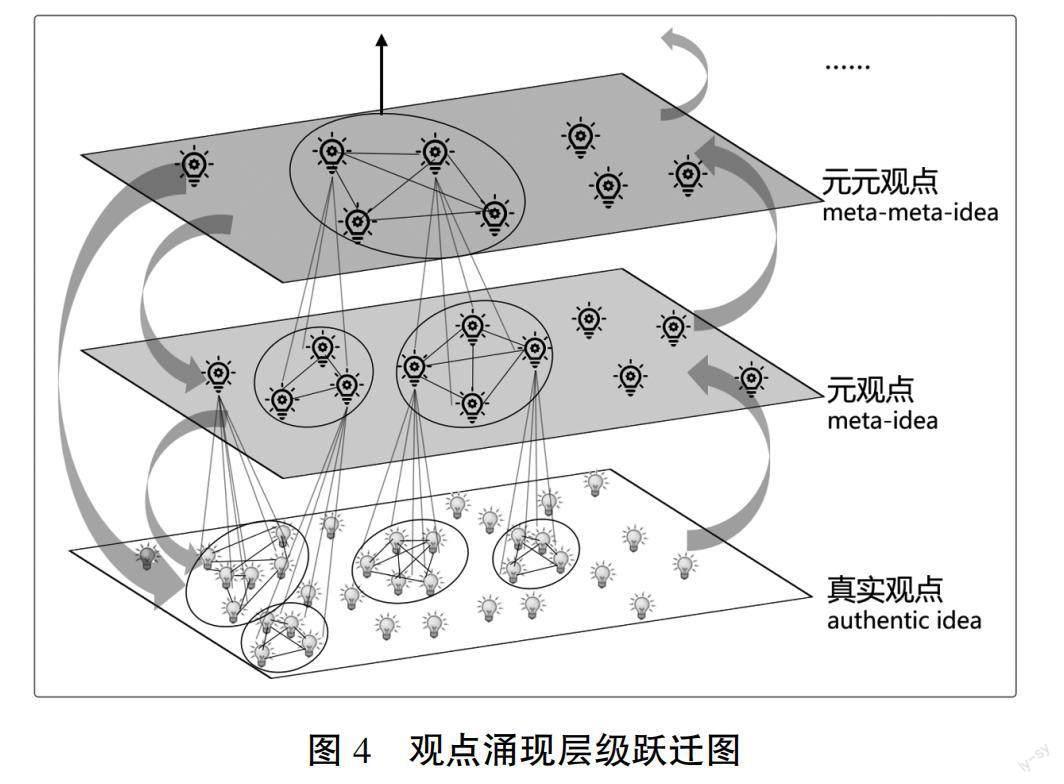
观点通过能量交易而出现的繁殖实际上是观点涌现层级的跃迁,其跃迁过程如图4所示。真实观点层是观点涌现的原始材料,也是层级中的基本单位,更是KB学习的起点。作为复杂系统的行动主体,观点通过不断与其他观点积极互动来展示出涌现的潜力。低层级是生成较高层级的基础,较高层级对较低层级具有下向因果关系。真实的观点未被预先赋予已知的知识,相互作用也是在自组织的开放环境中进行,因此,其互动的结果充满了未知性与不确定性。
“Meta”根源于希腊文,作为前缀本身具有After、Beyond、Changed、Higher等含义,在学术领域使用较为广泛,一般被表达为“Meta **=** of/about **”,常译为元**,如Metacognition译为元认知,亦常被解释为认知的认知。许多学者将涌现与“元**”的概念联系起来,复杂理论的先驱霍兰德将复杂适应系统中更高一级的主体称为元主体(Meta-Agents),元主体能够涌现出单个主体所不具备的属性,经再次聚集能够生成元—元主体(Meta-Meta-Agents),甚至会有元—元—元主体(Meta-Meta-Meta-Agents)。这个过程经过多次重复,就是复杂系统中典型的涌现层次,本研究中主体即观点。元系统跃迁理论也解释了生命科学、社会学等多个领域作为复杂系统的涌现层次。莫兰认为元系统是一个能够把系统作为认识对象来处理的系统,从它产生元观点就表明主体的认识结构已被扩充,立足于新的理论基础之上,而认识永远是开放的、动态发展的、未完成的。元系统本身又只能从一个元元系统出发来审查自己,如此反复,以至无穷。
元观点(Meta-Idea)代表了对初始观点的反思、综合、升华与创新,是高一级的涌现形式。元观点又和其他层级的观点进行能量交易,生成元—元观点(Meta-Meta-Idea),又是一个新的涌现层级。层级之间具有不可还原性,即“Meta-”层级是涌现的结果,新的整体模式不断出现。可以说,观点涌现是来自低层次观点、属于高层次观点、又不能完全用低层次观点解释的构型。KB教学中教师要鼓励学生产生观点并持续推进,真正重要的不是学生掌握了多少概念,而是帮助其生成“Meta-”层级的观点,从而达到观点涌现层级的跃迁。教师要敏锐地洞察到社区中观点的跃迁,如学生最初的观点可能只是阐述了某领域范畴中的一个特例,而涌现出的元观点拥有更广阔的视域,具有比某一类认识对象更广泛的适用性,向上为生成独特的理论体系奠定基础,向下则可以为某个真实情境中的现实问题提供解决思路和方法。
(三)从化繁为简到化简为繁的思路推进了研究视角的转变
在复杂性科学第三波浪潮的冲击下,整体不能还原为部分元素,部分也不能通过叠加成为整体,已经逐渐成为共识。“复杂”不再是被回避、被还原、被企图消除、被妖魔化的,而是被正视、被构造、被生成、被正名的,更是在理念和研究方法层面都必须清晰解读的领域。研究将复杂性科学引入到KB对观点涌现的探索中,推进了研究视角的转变,同时为KB的12条原则提供了复杂性科学视角的解读,如权威性资料的建构性引入实际上是为观点互动形成的复杂适应系统引入“负熵”,为观点群逐渐走向有序提供能量。深入挖掘和揭示观点涌现的内部机理,将帮助教师认清观点改进中的复杂性特征,为教师教学策略的调整提供依据,从而破解KB教学过程的观点群相互作用中千变万化、难以把握的难题。
[参考文献]
[1] 埃德加·莫兰.复杂性理论与教育问题[M].陈一壮,译.北京:北京大学出版社,2004:6,9.
[2] WIDEEN M, MOON M S. A critical analysis of the research on learning to teach: making the case for an ecological perspective on inquiry[J]. Review of educational research, 1998,68(2):130-178.
[3] PAAVOLA S, HAKKARAINEN K. The knowledge creation metaphor -an emergent epistemological approach to learning[J]. Science & education, 2005,14(6):535-557.
[4] LOSSMAN H, SO H J. Toward pervasive knowledge building discourse: analyzing online and offline discourses of primary science learning in Singapore[J]. Asia Pacific education review, 2010,11(2):121-129.
[5] SAWYER R K. Social emergence: societies as complex systems[M]. New York: Cambridge University Press, 2005: 10.
[6] 費军,陈绵云,宋业新,张曙红.系统管理学的演化与进展[J].科技进步与对策,2003,20(6):173-175.
[7] 周加仙.一九九〇年代以来世界学习科学的发展及其对教育的启示[J].教师月刊,2019(8):8-25.
[8] FORSMAN J, MOLL R, LINDER C. Extending the theoretical framing for physics education research: an illustrative application of complexity science[J]. Phys.rev.st phys.educ.res, 2014,10(2):020122.
[9] JACOBSON M J, LEVIN J A, KAPUR M. Education as a complex system: conceptual and methodological implications[J]. Educational researcher,2019,48(2):112-119.
[10] SAWYER R K. The Cambridge handbook of the learning sciences[M]. Cambridge: Cambridge University Press, 2014:319
[11] 李曙华,李洋,桑新民.探索MOOCs与现实课堂结合的教学模式——系统科学与圣塔菲网络课程的个案研究[J].远程教育杂志,2014,32(5):17-23.
[12] 田浩,武法提.复杂性科学视域下的学习干预:概念解析、核心要素及模型构建[J].电化教育研究,2022,43(9):29-36.
[13] L.P.斯特弗,J.盖尔.教育中的建构主义[M].高文,徐斌艳,程可拉,译.上海:华东师范大学出版社,2002:205-206.
[14] STAHL G. Group cognition in computer-assisted collaborative learning[J]. Journal of computer assisted learning, 2010,21(2):79-90.
[15] JOHNSON S. Emergence: the connected lives of ants, brains, cities, and software[M]. New York: Scribner. 2001:50.
[16] FISCHER F, GOLDMAN S R. International handbook of the learning sciences[M]. London: Taylor & Francis Group, 2018: 140.
[17] SCARDAMALIA M, BEREITER C. Knowledge building[C]. GUTHRIE J W(Ed.), Encyclopedia of education (2nd ed). New York: Macmillan. 2003: 1370-1373.
[18] LI Y, KETTINGER W J. An evolutionary information-processing theory of knowledge creation[J]. Journal of the association for information systems, 2006,7(9):593-617.
[19] GOURLAY S. Conceptualizing knowledge creation: a critique of Nonaka's theory[J]. Journal of management studies, 2006,43(7): 1415-1436.
[20] KRAUSKOPF K, BERTRAM J, HSIAO Y, et al. Memetic processes as conceptual framework for idea improvement in knowledge building[J]. Security & communication networks, 2012,6(3):373-383.
[21] BEREITER C. Education and mind in the knowledge age[M]. New Jersey: Lawrence Erlbaum Associates, 2002:200-203.
[22] 李海峰,王煒.自组织视域下的在线深度协作知识建构研究[J].中国远程教育,2019(1):47-57.
[23] HONG H Y, SCARDAMALIA M, ZHANG J W. Knowledge society network: toward a dynamic, sustained network for building knowledge [J]. Canadian journal of learning & technology, 2007,36(1):29.
[24] 蒋纪平,胡金艳,张义兵.知识建构学习社区中“观点改进”的发展轨迹研究[J].电化教育研究,2019,40(2):21-29.
[25] ERKUNT H. Emergence of epistemic agency in college level educational technology course for pre-service teachers engaged in CSCL[J]. Turkish online journal of educational technology,2010, 9(3):38-51.
[26] BEDEAU M. Weak emergence[J]. Philosophical perspectives,1997(11):375-399.
[27] 集智俱乐部.NetLogo多主体建模入门[M].北京:人民邮电出版社,2021:66,145.
[28] 梅拉妮·米歇尔.复杂[M].唐璐,译.长沙:湖南科学技术出版社,2011:53.
[29] 张守凤, 周丽华,武杰.熵与势概念的沟通——信息在系统演化中的作用[J].山东社会科学,2021(9):174-181.
[30] SHANNON C E. A Mathematical theory of communication[J]. Reprinted with corrections from the bell system technical journal, 1948,27:379-423.
[31] CHU J, EVANS J. Slowed canonical progress in large fields of science[J]. Proceedings of the national academy of sciences, 2021,118 (41):1-5.
[32] ZENG A, FAN Y, DI Z, WANG Y, HAVLIN S. Fresh teams are associated with original and multidisciplinary research[J]. Nature human behaviour, 2021(10):1314-1322.
[33] 理查德·道金斯.自私的基因[M].卢允中,张岱云,陈复加,罗小舟,叶盛,等译.北京:中信出版社,2018:221-230.
[34] 钱吴永,党耀国,刘思峰.含时间幂次项的灰色GM(1,1,t~α)模型及其应用[J].系统工程理论与实践,2012,32(10):2247-2252.
[35] 約翰·H.霍兰德.隐秩序:适应性造就复杂性[M].周晓枚,韩晖,译.上海:上海科技教育出版社,2000:11-12.
Construction of Idea Emergence Model Supported by Multi-agent Simulation in Knowledge Building Community: A Perspective of Complexity Science
HU Jinyan, YANG Xia, GAO Xingqi, MAN Qifeng, ZHANG Yibing
(1.Faculty of Education, Henan Normal University, Xinxiang Henan 453007;
2.Faculty of Management, Xinxiang Medical College, Xinxiang Henan 453003;
3.School of Education Science, Nanjing Normal University, Nanjing Jiangsu 210097)
[Abstract] Idea-centered knowledge construction theory emphasizes that learners explore real problems like scientists. The continuous interaction of multiple ideas makes the community gradually evolve into a complex system, and the non-superpositional ideas present an emergent phenomenon that cannot be reduced. However, the current research on emergence of ideas stops at the conceptual understanding of its systematic properties, and still follows the research perspective and paradigm of reductionism, cutting the complex emergence phenomenon into a single idea or even fragmented keywords for mining and analyzing, which fails to truly touch the essence of idea emergence. Based on this, this study adopts bottom-up multi-agent modeling to explore the law and characteristics of idea emergence. It is found that the higher the level of idea emergence is, the longer the time required and the greater the difficulty. Higher-level ideas limit the interaction domain of lower-level ideas. The energy value in the process of idea emergence shows an imbalance from normal distribution to exponential distribution. This paper provides a new perspective and method for the study of idea emergence, and has multi-level explanatory power for the teaching practice of knowledge building community.
[Keywords] Knowledge Building; Idea Emergence; Multi-agent Simulation; Complexity Science
