考虑应力敏感的致密储层油水两相相对流动能力分形数值模拟方法
2024-01-22王嘉新蒋丽丽魏金阳刘宗科王泽川
王嘉新,田 冷,蒋丽丽,魏金阳,刘宗科,王泽川
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学(北京) 石油工程学院,北京 102249; 3.中国石油长庆油田公司 勘探开发研究院,陕西 西安 710018)
引 言
致密油藏是非常规能源开发的热点领域,由于其储层物性较差,非均质性较强,需经过压裂改造才能形成工业产能[1-2]。致密储层具有低孔、超低渗的特点,油水均存在于亚微米-纳米尺度的孔隙中,油水两相渗流机理和流动特征尤为复杂[3-4]。因此,油水两相相对渗透率作为表征致密储层流体渗流特征的关键参数,是预测油井产量和开发方案制定与调整的重要指标[5-7]。
目前,国内外学者对于致密储层油水两相相渗的研究多采用是实验法[8-15]和数学模型法[16-18]。实验方法昂贵、费时,而且选取的岩心只是很小一部分,很难表示研究区域的整体特征,因此数学模型法得到了广泛应用[19-21]。由于多孔介质空间孔隙分布特征与矿物颗粒的分布特征相似,分形理论被广泛应用于致密储层油水渗流机理研究中[22]。此外,致密储层普遍存在应力敏感效应,且应力变化会对储层孔隙结构特征产生重要影响,进而影响渗流特征和油井产量[2]。因此,建立考虑应力敏感的致密储层油水两相相对渗透率模型具有重要的现实意义。
本文基于分形理论,根据致密储层孔隙结构的分形特征,将孔喉等效为尺寸不规则的毛细管束,建立了考虑应力敏感的致密储层油水两相相对渗透率模型,研究了有效应力、弹性模量和孔隙度对致密储层油水两相相渗曲线的影响,揭示了致密储层油水两相渗流机制和流动特征,为致密油藏产能预测、开发方案制定与调整提供理论支持。
1 分形理论
研究表明从纳米到微米尺度范围内,多孔介质内部空间具有分形特征,因此多孔介质的微观孔隙结构及孔隙尺寸分布亦具有分形特征[23]。根据分形理论,孔隙半径大于或等于r的累积孔隙数量与孔隙半径之间满足分形规律[24],即
N(ξ≥r)=(rmax/r)Df。
(1)
式中:N为累积孔隙数量;ξ为孔隙半径尺寸;r为孔隙半径,μm;rmax为最大孔隙半径,μm;Df为孔隙分形维数,在二维空间中,Df取值0~2。因此,从最小孔隙半径rmin到最大孔隙半径rmax,总的孔隙数目为[25]
N=(rmax/rmin)Df,
(2)
对r求导,可得
(3)
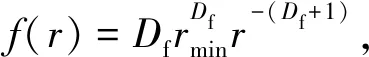
根据分形理论,孔隙分形维数Df可表达为[25]
(4)
式中:φ为孔隙度,%;d为欧几里得维数,在二维和三维空间下,d分别取值为2和3。
利用毛管束对多孔介质中的孔隙喉道进行表征,由于多孔介质中的孔喉迂回弯曲,毛细管的实际长度L要大于其表征长度L0(即毛细管沿流动方向的直线长度),毛细管长度与其半径可用分形幂规律表示[24-25],即
(5)
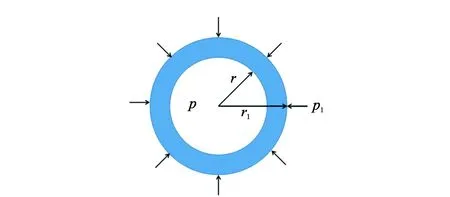
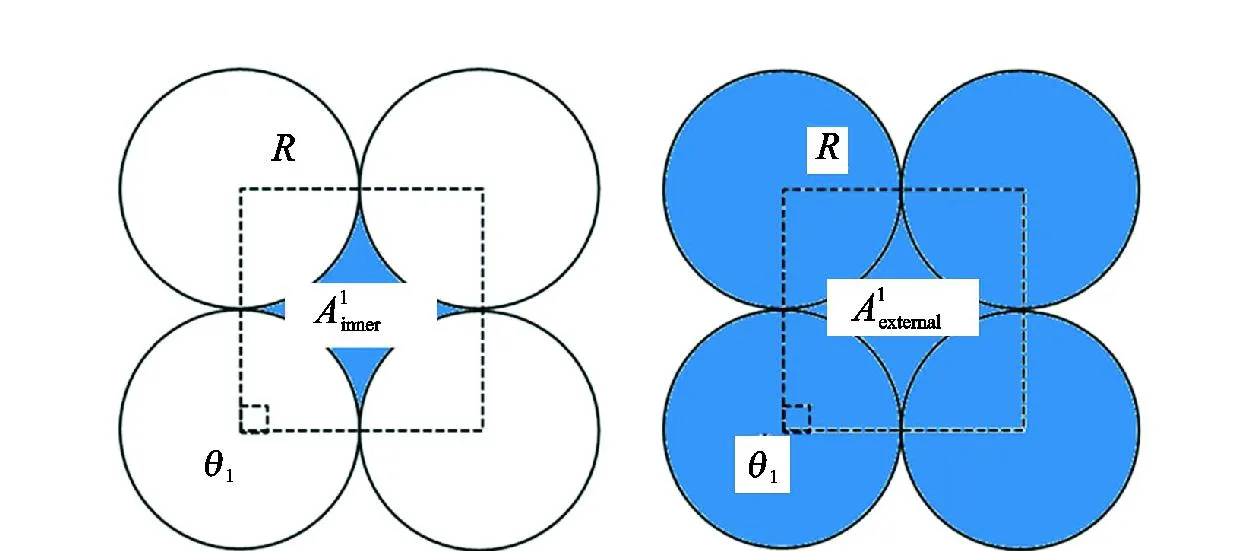
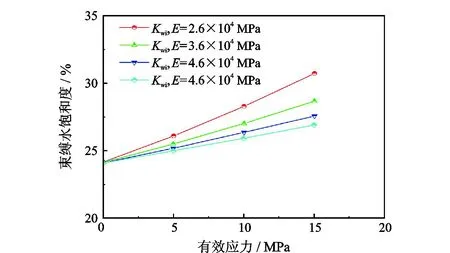
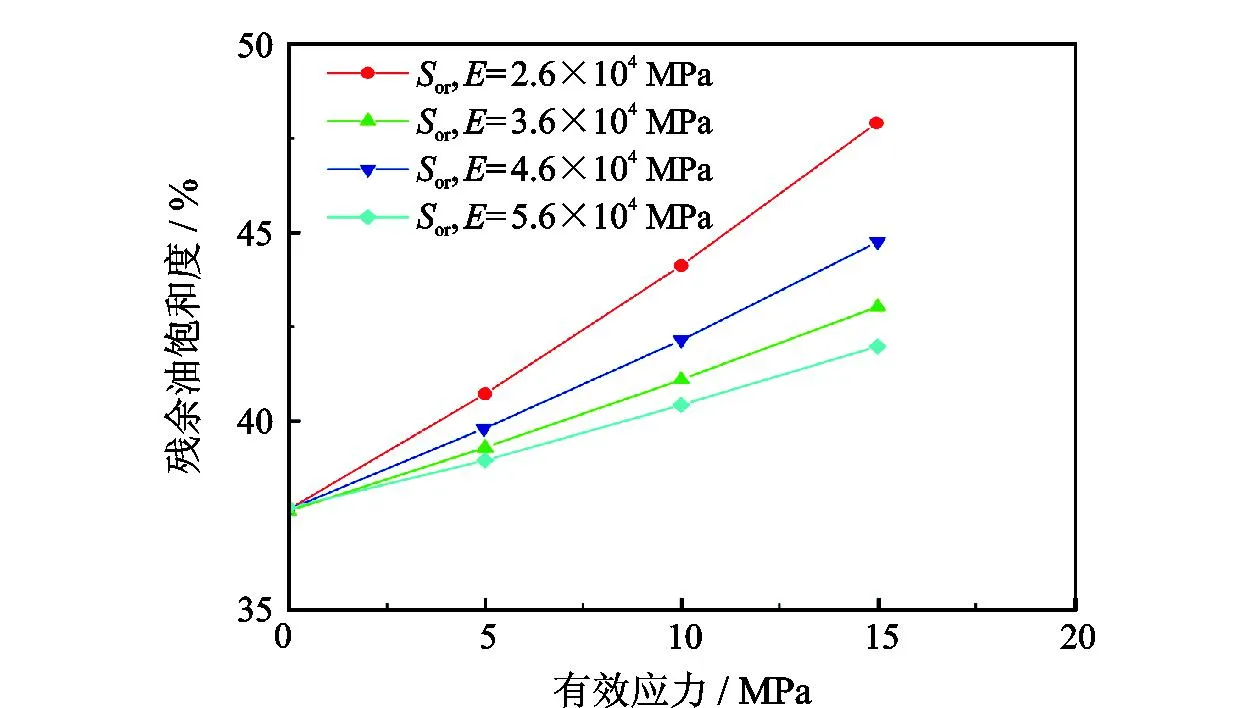
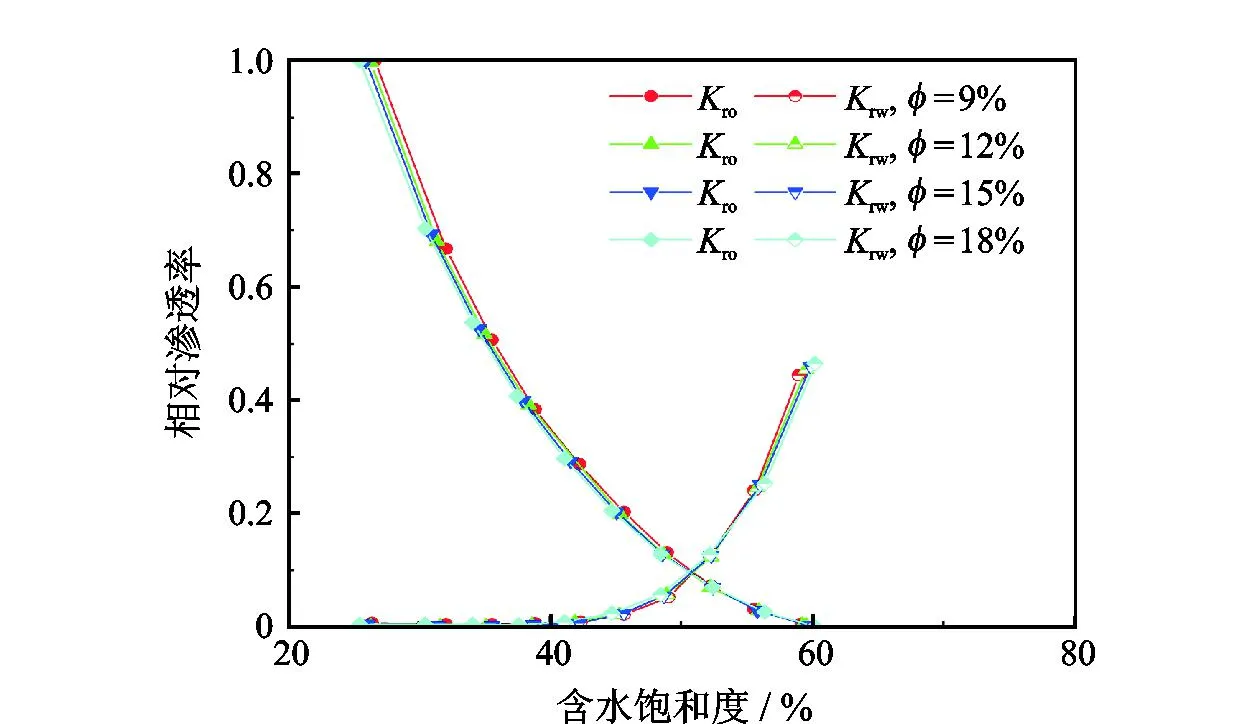
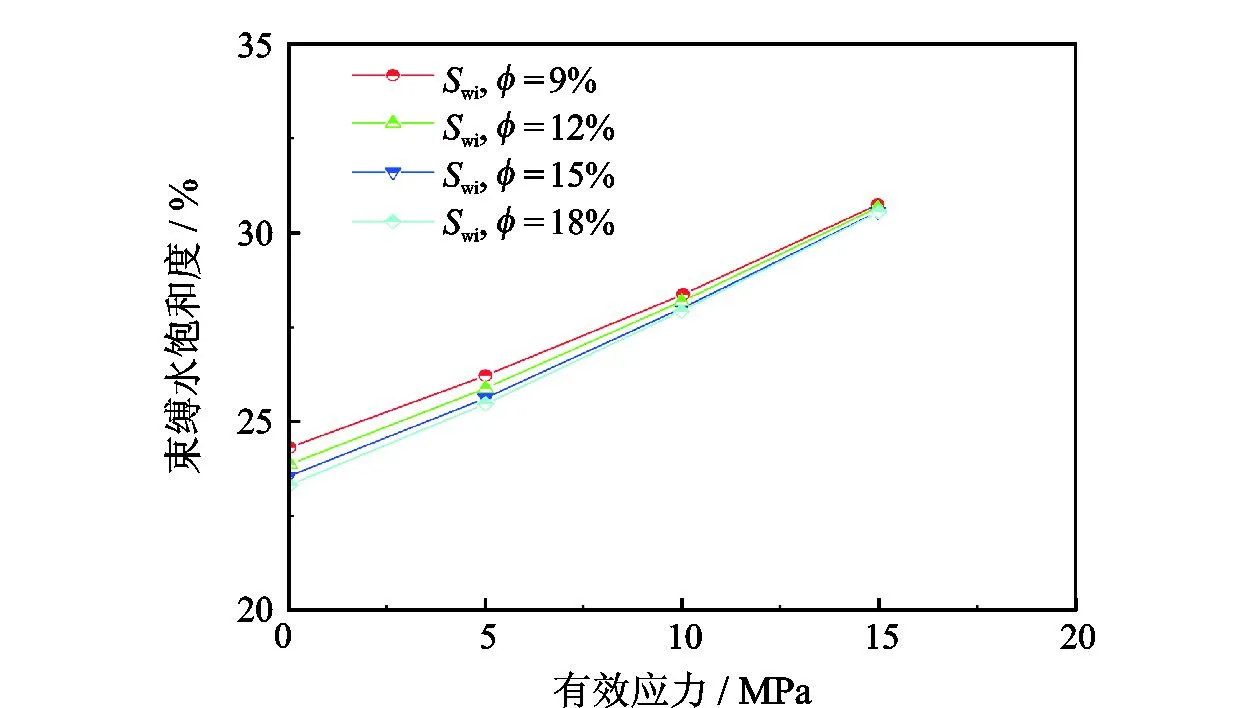
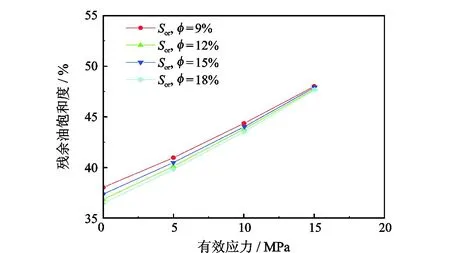
式中,DT为迂曲度分形维数,在二维空间中1 (6) 其中 (7) 迂曲度的表达式为 (8) 毛管束沿流动方向的长度L0计算公式为[23] (9) 式中,A为毛细管束横截面积,μm2。 相对渗透率模型假设条件为: (1)致密砂岩孔喉由不等径并且迂曲的毛细管组成,毛细管半径及长度符合分形特征; (2)流体在毛细管内发生层流流动,水为润湿相,油为非润湿相; (3)rc为临界毛细管半径,半径大于rc的毛细管为油相流动通道,半径小于rc的毛细管为水相流动通道,单一毛细管中只有单相流体流动; (4)束缚水及残余油以边界层的形式附于毛细管壁内侧; (5)油相和水相为牛顿流体,油水之间不存在相交换。 流体在岩石中的流动通道由毛管束表征,那么长度为L,半径为r的单个毛细管的体积为 V=πr2L, (10) 因此,N根毛细管的总体积为 (11) 束缚水和残余油以边界层的形式附着在管壁内侧。边界层所占的毛细管体积为 (12) 式中,δ为边界层厚度,μm。 根据假设,半径小于rc的毛细管为水相流动通道,则可流动的水相体积为 (13) 由饱和度的定义得到边界层流体饱和度Sδ及可流动水相饱和度Sw1分别为 (14) (15) 束缚水饱和度、残余油饱和度与边界层流体饱和度之比与润湿性满足关系 (16) (17) Sw=Sw1+Swc。 (18) 由哈根-泊肃叶方程可得,油、水两相总流量分别为 (19) (20) 同时,由达西方程可得油、水两相总流量分别为 (21) (22) 式中:Kw为水相有效渗透率,μm2;Ko为油相有效渗透率,μm2;Δpw为水相的压差,MPa;Δpo为油相的压差,MPa;μw为水相的黏度,mPa·s;μo为油相的黏度,mPa·s。 束缚水条件下时,水相不流动,油相占据整个可流动空间。则由式(20)和式(22)可得束缚水条件下的油相有效渗透率 (23) 结合公式(19)-(23),可得归一化的油水相对渗透率 (24) (25) 油水流动以及分布状态与上述模型的假设条件一致,此时毛细管壁具有一定的厚度,如图1所示。毛细管内径为r,外径为r1,毛细管外部压力为p1,内部压力为p。根据弹性力学厚壁筒理论,可得毛细管应力应变关系[26] 图1 单一毛管受力示意图 (26) 式中:Δr为毛管内半径变形量,μm;E为岩石弹性模量,GPa;v为岩石泊松比;r1为毛管外径,μm;p为毛细管内部压力,MPa;p1为毛细管外部压力,MPa。 当外部压力恒定时,则应力变化后的毛细管内径变化为 (27) 图2 四根等直径的平行毛细管束堆积模型示意图 (28) (29) 假设厚壁筒内径面积为Ainner,外径面积为Aexternal,则两者分别为 Ainner=πr2; (30) Aexternal=πr12。 (31) 根据等效面积原理,厚壁筒内径r与外径r1的关系为 (32) 则公式(27)可变形为 (33) 假设孔隙数目在应力变化前后不变,根据式(33)可得 (34) 由式(34)可得应力变化后的孔隙分形维数 (35) 结合式(32)和式(35)可得应力变化后的孔隙度 (36) 同理,应力变化后迂曲度分形维数为 (37) 其中 (38) (39) (40) (41) (42) (43) 与式(19)-(23)的推导过程相同,可得到应力变化后的油水相对渗透率分别为 (44) (45) 选取鄂尔多斯盆地合水地区的H1井1块长度为5 cm、直径为2.5 cm的致密砂岩岩心,岩心的孔隙度和渗透率分别为10.34%和0.29×10-3μm2。为了更好地与建立的模型结果作对比,依据行标GB/T 28912-2012采用稳态法进行两相相对渗透率测试,实验流程见图3,主要实验步骤如下: 图3 稳态法测相对渗透率流程 (1)岩心制备、清洗; (2)测定绝对渗透率,把饱和地层水的岩心装入夹持器,加2 MPa围压,加热岩心至地层温度(60 ℃),用水测定岩心100%饱和水时的绝对渗透率; (3)用泵以恒定的排量分别将油和水注入岩心; (4)当岩样出口油、水流量分别等于注入的油、水流量时,表明岩心中油水两相达到稳定状态,此时测量岩心两端压差和油水各自的流量,并由累计产出的油水量,用称重法计算含水饱和度; (5)根据以上数据算出一个含水饱和度下的油、水相对渗透率; (6)改变泵的排量,即改变注入岩心的油水比例,即改变注入岩心的油水比例,重复上述(3)-(5)过程,得到另一个含水饱和度下的油、水相对渗透率; (7)多次重复以上过程,便可得到一组含水饱和度下的油、水相对渗透率,从而得到相对渗透率曲线。 根据岩心相渗实验数据与模型计算结果进行对比,验证该模型的准确性,对比结果如图4所示。对比结果表明:模型预测结果与实验结果具有良好的一致性,验证了该模型是准确可靠的。 图4 相对渗透率实验结果与模型预测结果对比 4.2.1 有效应力 图5为不同有效应力下的相对渗透率曲线,可以看出:相渗曲线形态随有效应力改变会发生较大变化,随着有效应力的增加,残余油下的水相相对渗透率降低,束缚水饱和度及残余油饱和度增加,相渗曲线向中间收缩。由于有效应力的增加,毛管内径会受压收缩,边界层厚度随着毛管半径的减小而相对增加,导致束缚水和残余油饱和度上升,共渗区变窄。在相同含水饱和度下,水相相对渗透率与等渗点左边的油相相对渗透率随有效应力的增加而上升。有效渗透率下降而相对渗透率上升,意味着束缚水下的油相有效渗透率下降程度,比任意饱和度下的油水两相有效渗透率下降程度高,说明虽然油水流动能力降低,但相对流动能力增加。此外,同一饱和度下等渗点右边的油相相对渗透率降低,表明在等渗点之后,油相相对流动能力随有效应力增加而急剧下降。 图5 有效应力与相对渗透率的关系 4.2.2 弹性模量 弹性模量与油水相对渗透率的关系如图6所示。弹性模量影响着孔隙喉道变形的程度,弹性模量越低,孔隙喉道受力变形越大。随着弹性模量的增加,束缚水饱和度及残余油饱和度降低,相渗曲线呈现外扩的趋势。并且,弹性模量对驱替初期的油相相对渗透率影响较大,但对水相相对渗透率影响较小,而弹性模量对驱替后期的水相相对渗透率影响较大,但对油相相对渗透率影响较小。 图6 弹性模量与相对渗透率的关系 图7和图8分别为不同弹性模量下束缚水及残余油饱和度随有效应力的变化关系。束缚水和残余油饱和度随着有效应力的增加而上升,相同有效应力下,弹性模量越小,束缚水和残余油饱和度越高。同时,弹性模量越小,束缚水和残余油饱和度随有效应力变化越明显。束缚水饱和度最大变化约6%,而残余油饱和度最大变化约10%,弹性模量和有效应力对残余油饱和度的影响更为明显。 图7 不同弹性模量束缚水饱和度与有效应力的关系 图8 不同弹性模量残余油饱和度与有效应力的关系 4.2.3 孔隙度 图9为不同初始孔隙度下的相渗曲线。由图9可以看出:随着孔隙度的增加,相渗曲线向外扩展,然而,变化幅度很小。孔隙度对驱替前期的油相相对渗透率和驱替后期水相相对渗透率有影响,但影响程度不高。总体来看,孔隙度对相渗曲线影响并不显著。 图9 初始孔隙度与相对渗透率的关系 图10和图11分别为不同初始孔隙度下束缚水及残余油饱和度随有效应力的变化关系。初始孔隙度不同,初始束缚水及残余油饱和度不同,孔隙度越大,束缚水及残余油饱和度越低。随着有效应力的增加,束缚水和残余油饱和度增加,不同孔隙度下的束缚水和残余油饱和度趋向一个值。当有效应力增加到一定值后,岩石孔隙结构很难被压缩,此时孔隙度趋于稳定。 图10 束缚水饱和度与不同有效应力和初始孔隙度的关系 图11 剩余油饱和度与不同有效应力和初始孔隙度的关系 (1)基于分形理论建立的考虑应力敏感的致密储层油水两相相对渗透率模型,与相渗实验数据吻合程度高,验证了模型的准确性,能够有效表征致密储层油水两相的渗流特征。 (2)随着有效应力的增大,束缚水饱和度和剩余油饱和度均降低,油水相对渗透率曲线向中间收缩,共渗区域减小;随着弹性模量的降低,多孔介质的变形量、束缚水和残余油饱和度均增加,油水相对渗透率曲线呈现外扩的趋势;孔隙度对油水相对渗透率的影响较小。2 分形毛管束相渗模型
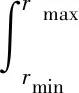
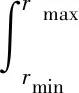


3 考虑应力敏感的相对渗透率模型

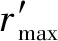

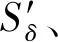
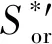
4 模型验证及敏感性因素分析
4.1 模型验证
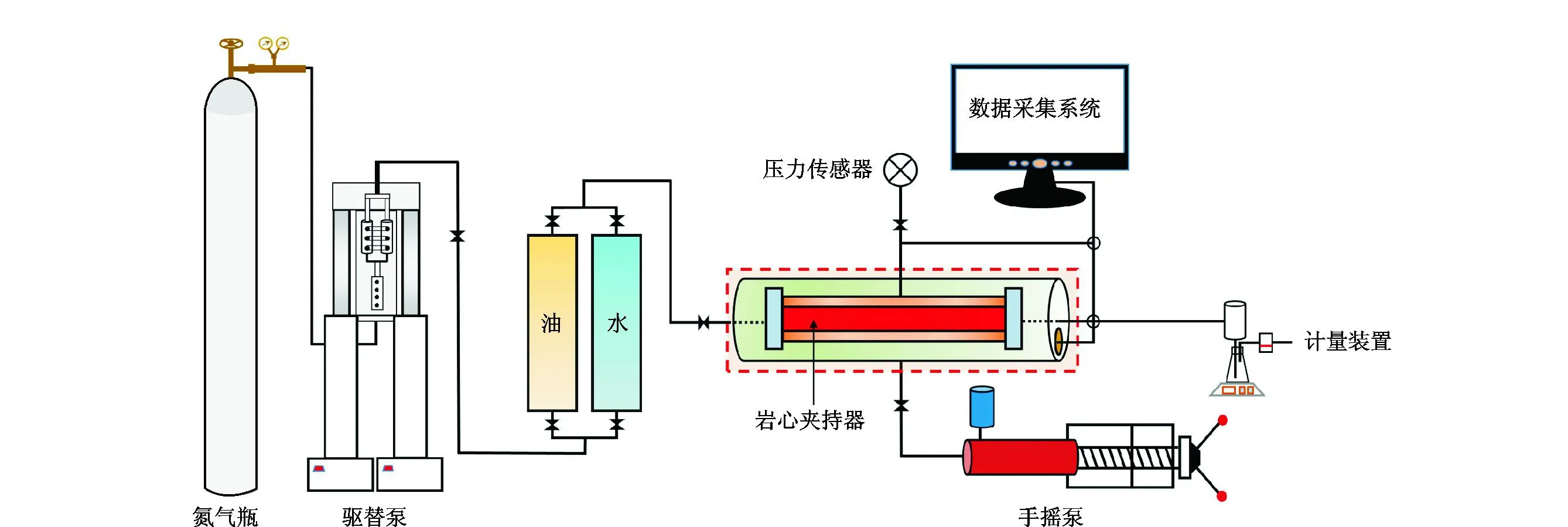
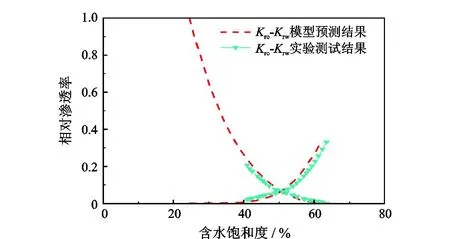
4.2 参数敏感性分析
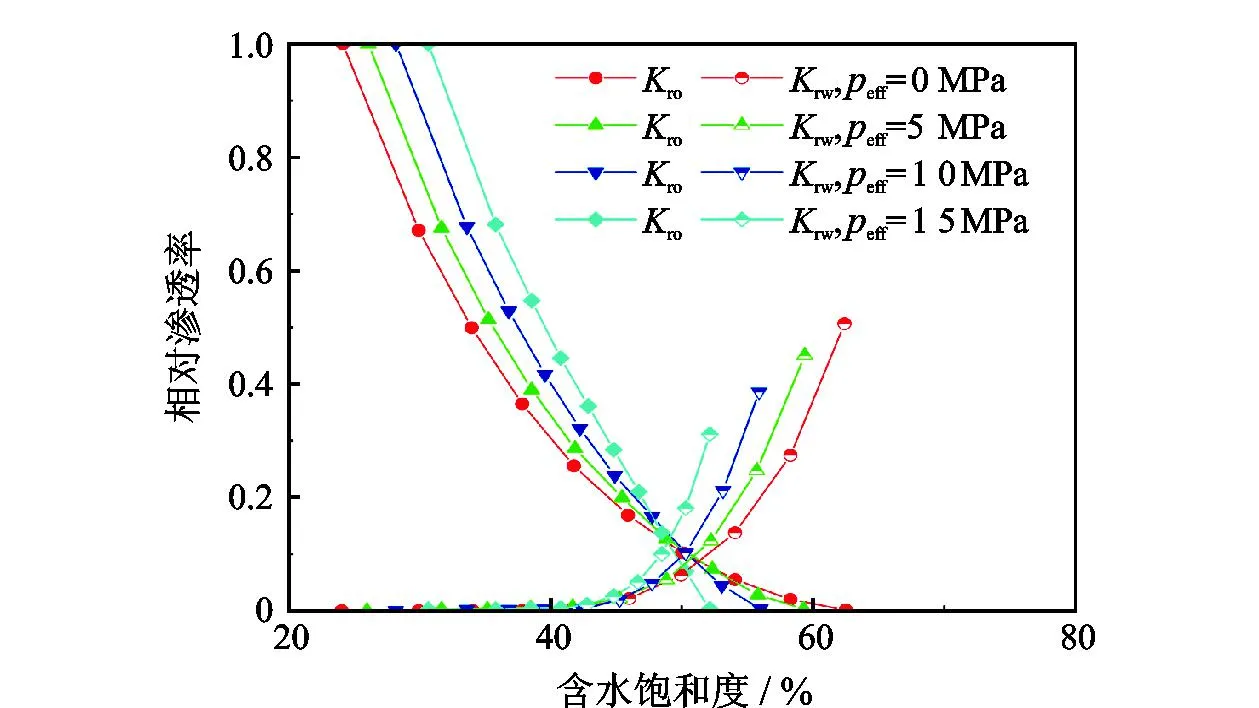
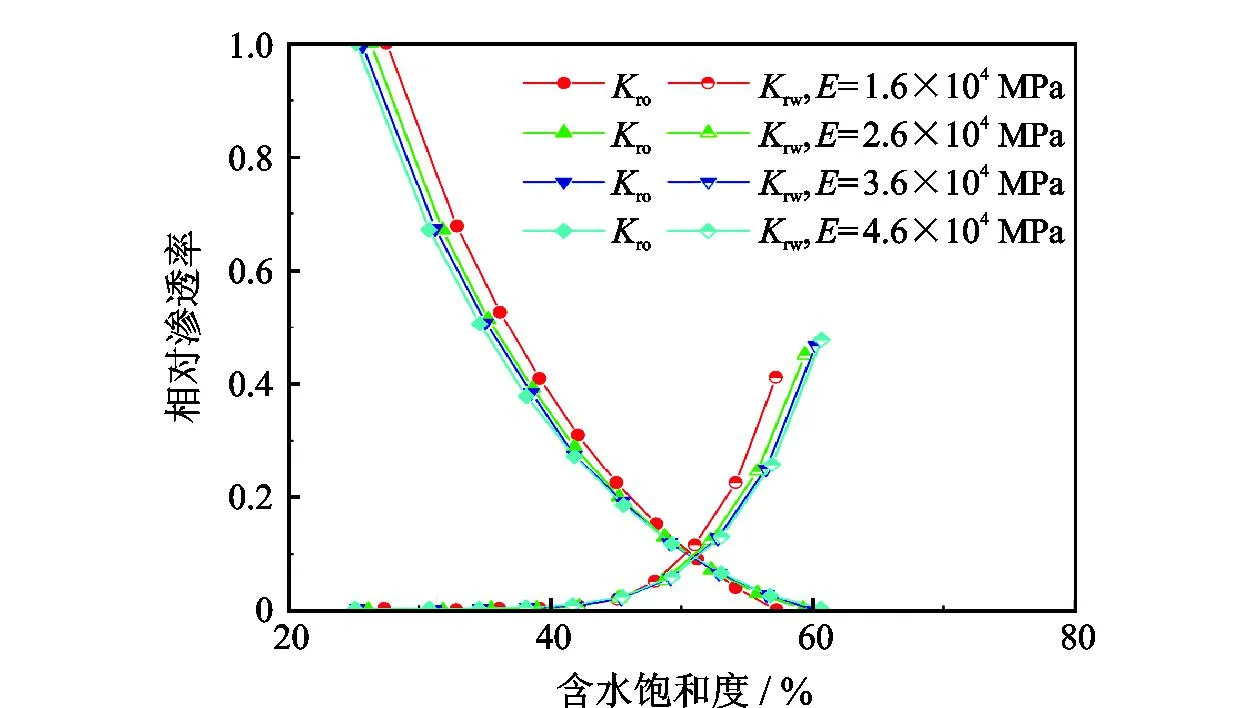
5 结 论
